北师大版数学六年级下册 总复习-式与方程 第一课时 式与方程 课件(28张ppt)
文档属性
| 名称 | 北师大版数学六年级下册 总复习-式与方程 第一课时 式与方程 课件(28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 14:24:10 | ||
图片预览







文档简介
(共28张PPT)
总 复 习
式与方程
第一课时 式与方程
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
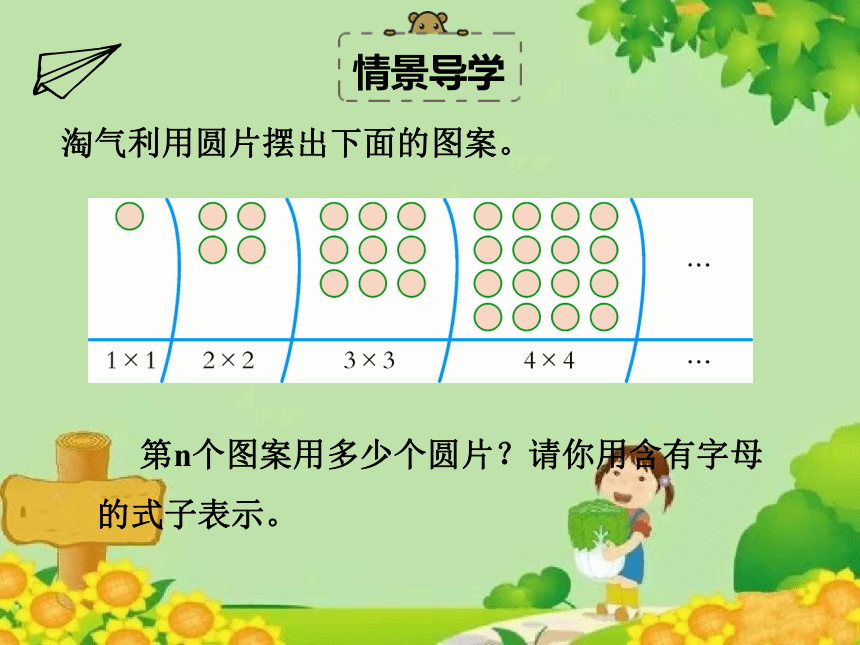
第n个图案用多少个圆片?请你用含有字母的式子表示。
淘气利用圆片摆出下面的图案。
探索与发现
02
探索与发现
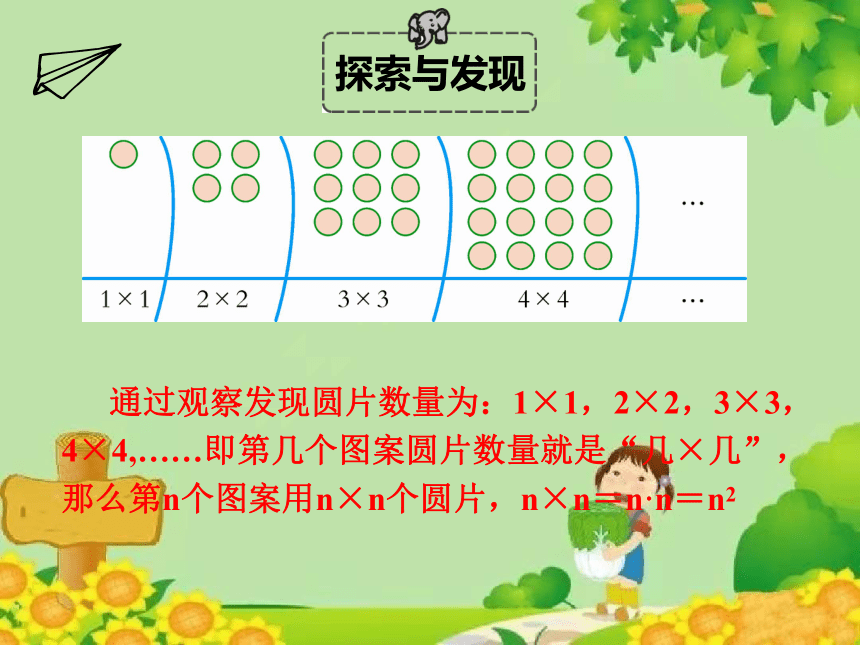
通过观察发现圆片数量为:1×1,2×2,3×3,4×4,……即第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2
探索与发现
生活中还有哪些规律能利用这个式子表示?
正方形的面积可以用n2表示:正方形的边长是n,正方形的面积=边长×边长=n×n=n2;
方阵的人数可以用n2表示:方阵每排有n人,一共有n排,那么总人数为n×n=n2。
探索与发现
我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c + b×c
运算定律:
周长公式:
长方形的周长:
正方形的周长:
圆的周长:
C=(a+b)×2
C=4a
C=πd
或 C=2πr
面积公式:
长方形的面积:
正方形的面积:
平行四边形的面积:
三角形的面积:
梯形的面积:
圆形的面积:
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
体积公式:
长方体的体积:
正方体的体积:
V=abh
圆柱的体积:
圆锥的体积:
V=a3
V=πr2h
V=Sh
V= πr2h
3
1
探索与发现
解下面的方程,并说一说你是怎么解的。
解:
9x-1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x-1.8=5.4 0.8x+1.2x=25
解:
(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
探索与发现
1.等式与方程
(1)等式的意义:表示相等关系的式子叫作等式。
(2)方程的意义:含有未知数的等式叫方程。
(3)等式与方程的关系:方程一定是等式,等式不一定是方程。
探索与发现
2.方程的解和解方程
(1)方程的解的意义:使方程左右两边相等的
未知数的值,叫作方程的解。
(2)解方程的意义:求方程的解的过程叫作解
方程。
(3)解方程的依据:等式的基本性质(等式的
左右两边同时加上或减去同一个数,等式
的左右两边仍然相等;等式的左右两边同
时乘或除以一个不为0的数,等式的左右两
边仍然相等)。
探索与发现
列方程解应用题的步骤:
一般分5步:
1)根据题意,解设未知数为x .
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
探索与发现
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数是橘子箱数的 。商店购进了多少箱橘子?
解:设商店购进了x箱橘子。
橘子箱数× =苹果箱数
x=20
x=20÷
x=25
答:商店购进了25箱橘子。
探索与发现
(2)妙想和乐乐一共收集了128枚邮票,妙想收集的邮票数是乐乐的3倍。妙想、乐乐各收集了多少枚邮票?
解:设乐乐收集了x 枚邮票,妙想收集了3x 枚邮票。
乐乐收集的邮票+妙想收集的邮票=一共收集的邮票
x+3x=128
4x=128
x=128÷4
x=32
妙想:32×3=96(枚)
答:乐乐收集了32枚邮票,妙想收集了96枚邮票。
探索与发现
(3)淘气家和奇思家相距1240 m。一天,两人约定在两家之间的路上会合。淘气每分走75 m,奇思每分走80 m。两人同时从家出发,多长时间后能相遇?
解:设x分钟后相遇。
淘气走的路程+奇思走的路程=淘气家和奇思家相距的距离
75x+80x=1240
155x=1240
x=1240÷155
x=8
答:8分钟后相遇。
探索与发现
等式的性质
在等式的两边同时加上(或减去)一个相同的数,结果仍是等式。
在等式的两边同时乘(或除以)一个相同的数(零除外),结果仍是等式。
学以致用
03
学以致用
x-25
5n-m
2a+6
80%a
学以致用
2.5(a + b)
或
2.5(a + b)=
答:两地间的距离是262.5km。
2.5a + 2.5b
2.5×(45 + 60)=
262.5
学以致用
r
r
r
r
r
r
r
r
C=8r
S=4r2
或
C=4a
4×2r
8r
S=a2
=
=
=
a×a
=
2r×2r
=
4r2
学以致用
4
7
10
=1+3×1
=1+3×2
=1+3×3
n
(1) 1+3n
(2) 1+3n=1+3×100=301
答:需要301根小棒。
学以致用
5.解方程。
15x=60
x+2x=12.6
40%x=4.2
12+x=25
2x÷5=15
4x-1.6x=36
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
解: x=25-12
x=13
解:2x=15×5
2x=75
x=37.5
解: 2.4x=36
x=15
学以致用
60%x=1200
解: x=1200÷60%
x=2000
7s=4.2
解: s=4.2÷7
s=0.6
3x=x+10
解:2x=10
x=5
3x+x=11.2
解: 4x=11.2
x=2.8
学以致用
解:设每本丛书有 x 本。
8.2x+6.8x=120
15x=120
x=8
答:每本丛书有8本。
学以致用
9.甲、乙两个工程队同修一条公路,它们从两端同时施工。
(1)甲队每天修 a m,乙队每天修 b m,8天修完。这条公路长多少米?
(2)如果这条公路长3000m,甲队每天修85m,乙队每天修65m,修完这条公路需要多少天?
8(a+b)
答:这条公路长8(a+b)米 。
解:设修完这条公路需要 x 天。
(85+65)x=3000
150x=3000
x=20
答:修完这条公路需要20天。
学以致用
解:设原正方形的边长是 x 厘米。
答:原正方形的边长是9厘米。
x+ x=48÷4
x=12
x=9
3
1
3
4
课后作业
04
感 谢 观 看
总 复 习
式与方程
第一课时 式与方程
目 录
情景导学
1
探索与发现
2
学以致用
3
课后作业
4
情景导学
01
情景导学
第n个图案用多少个圆片?请你用含有字母的式子表示。
淘气利用圆片摆出下面的图案。
探索与发现
02
探索与发现
通过观察发现圆片数量为:1×1,2×2,3×3,4×4,……即第几个图案圆片数量就是“几×几”,那么第n个图案用n×n个圆片,n×n=n·n=n2
探索与发现
生活中还有哪些规律能利用这个式子表示?
正方形的面积可以用n2表示:正方形的边长是n,正方形的面积=边长×边长=n×n=n2;
方阵的人数可以用n2表示:方阵每排有n人,一共有n排,那么总人数为n×n=n2。
探索与发现
我们已经学过一些公式和规律,请你用含有字母的式子把它们表示出来。
加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c + b×c
运算定律:
周长公式:
长方形的周长:
正方形的周长:
圆的周长:
C=(a+b)×2
C=4a
C=πd
或 C=2πr
面积公式:
长方形的面积:
正方形的面积:
平行四边形的面积:
三角形的面积:
梯形的面积:
圆形的面积:
S=ab
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
体积公式:
长方体的体积:
正方体的体积:
V=abh
圆柱的体积:
圆锥的体积:
V=a3
V=πr2h
V=Sh
V= πr2h
3
1
探索与发现
解下面的方程,并说一说你是怎么解的。
解:
9x-1.8+1.8=5.4+1.8
9x=7.2
9x÷9=7.2÷9
x=0.8
9x-1.8=5.4 0.8x+1.2x=25
解:
(0.8+1.2)x=25
2x=25
2x÷2=25÷2
x=12.5
探索与发现
1.等式与方程
(1)等式的意义:表示相等关系的式子叫作等式。
(2)方程的意义:含有未知数的等式叫方程。
(3)等式与方程的关系:方程一定是等式,等式不一定是方程。
探索与发现
2.方程的解和解方程
(1)方程的解的意义:使方程左右两边相等的
未知数的值,叫作方程的解。
(2)解方程的意义:求方程的解的过程叫作解
方程。
(3)解方程的依据:等式的基本性质(等式的
左右两边同时加上或减去同一个数,等式
的左右两边仍然相等;等式的左右两边同
时乘或除以一个不为0的数,等式的左右两
边仍然相等)。
探索与发现
列方程解应用题的步骤:
一般分5步:
1)根据题意,解设未知数为x .
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
探索与发现
列方程解决下面的问题。
(1)果品商店购进20箱苹果。购进苹果的箱数是橘子箱数的 。商店购进了多少箱橘子?
解:设商店购进了x箱橘子。
橘子箱数× =苹果箱数
x=20
x=20÷
x=25
答:商店购进了25箱橘子。
探索与发现
(2)妙想和乐乐一共收集了128枚邮票,妙想收集的邮票数是乐乐的3倍。妙想、乐乐各收集了多少枚邮票?
解:设乐乐收集了x 枚邮票,妙想收集了3x 枚邮票。
乐乐收集的邮票+妙想收集的邮票=一共收集的邮票
x+3x=128
4x=128
x=128÷4
x=32
妙想:32×3=96(枚)
答:乐乐收集了32枚邮票,妙想收集了96枚邮票。
探索与发现
(3)淘气家和奇思家相距1240 m。一天,两人约定在两家之间的路上会合。淘气每分走75 m,奇思每分走80 m。两人同时从家出发,多长时间后能相遇?
解:设x分钟后相遇。
淘气走的路程+奇思走的路程=淘气家和奇思家相距的距离
75x+80x=1240
155x=1240
x=1240÷155
x=8
答:8分钟后相遇。
探索与发现
等式的性质
在等式的两边同时加上(或减去)一个相同的数,结果仍是等式。
在等式的两边同时乘(或除以)一个相同的数(零除外),结果仍是等式。
学以致用
03
学以致用
x-25
5n-m
2a+6
80%a
学以致用
2.5(a + b)
或
2.5(a + b)=
答:两地间的距离是262.5km。
2.5a + 2.5b
2.5×(45 + 60)=
262.5
学以致用
r
r
r
r
r
r
r
r
C=8r
S=4r2
或
C=4a
4×2r
8r
S=a2
=
=
=
a×a
=
2r×2r
=
4r2
学以致用
4
7
10
=1+3×1
=1+3×2
=1+3×3
n
(1) 1+3n
(2) 1+3n=1+3×100=301
答:需要301根小棒。
学以致用
5.解方程。
15x=60
x+2x=12.6
40%x=4.2
12+x=25
2x÷5=15
4x-1.6x=36
解:x=60÷15
x=4
解:3x=12.6
x=12.6÷3
x=4.2
解:x=4.2÷40%
x=10.5
解: x=25-12
x=13
解:2x=15×5
2x=75
x=37.5
解: 2.4x=36
x=15
学以致用
60%x=1200
解: x=1200÷60%
x=2000
7s=4.2
解: s=4.2÷7
s=0.6
3x=x+10
解:2x=10
x=5
3x+x=11.2
解: 4x=11.2
x=2.8
学以致用
解:设每本丛书有 x 本。
8.2x+6.8x=120
15x=120
x=8
答:每本丛书有8本。
学以致用
9.甲、乙两个工程队同修一条公路,它们从两端同时施工。
(1)甲队每天修 a m,乙队每天修 b m,8天修完。这条公路长多少米?
(2)如果这条公路长3000m,甲队每天修85m,乙队每天修65m,修完这条公路需要多少天?
8(a+b)
答:这条公路长8(a+b)米 。
解:设修完这条公路需要 x 天。
(85+65)x=3000
150x=3000
x=20
答:修完这条公路需要20天。
学以致用
解:设原正方形的边长是 x 厘米。
答:原正方形的边长是9厘米。
x+ x=48÷4
x=12
x=9
3
1
3
4
课后作业
04
感 谢 观 看
