8.4.2空间点、线、面之间的位置关系 课件(共20张PPT)
文档属性
| 名称 | 8.4.2空间点、线、面之间的位置关系 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 558.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 06:54:39 | ||
图片预览






文档简介
(共20张PPT)
空间点、线、面之间位置关系
人教版高一年级第二册
教学目标
1. 会判断空间两直线间的位置关系.
2.会判断直线与平面、平面与平面的位置关系.
3.会判断平面与平面的位置关系.
4.会用符号语言和图形语言表示两直线、直线和平面、平面和平面的位置关系.
新知导入
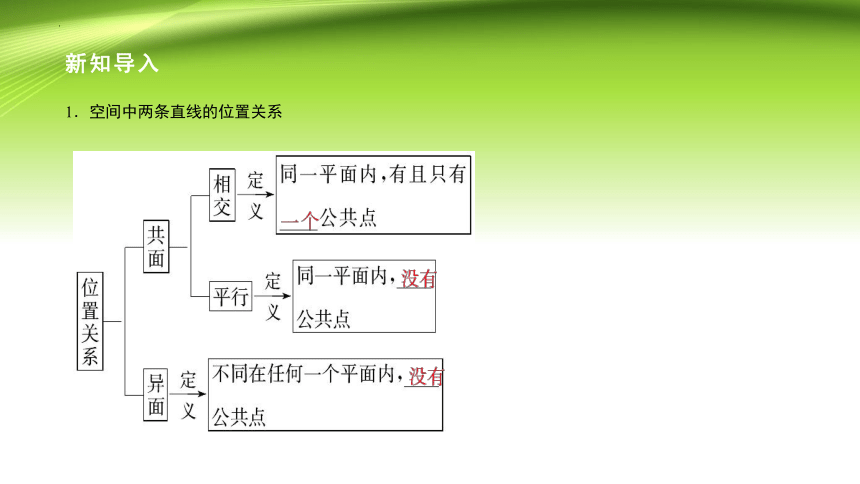
1.空间中两条直线的位置关系
新知讲解
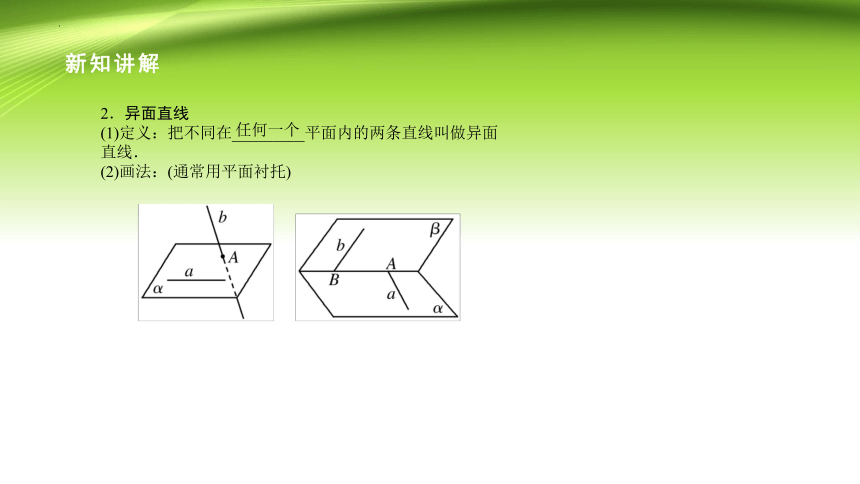
2.异面直线
(1)定义:把不同在_________平面内的两条直线叫做异面直线.
(2)画法:(通常用平面衬托)
任何一个
3.直线和平面的位置关系
无数
有且只有一
没有
新知讲解
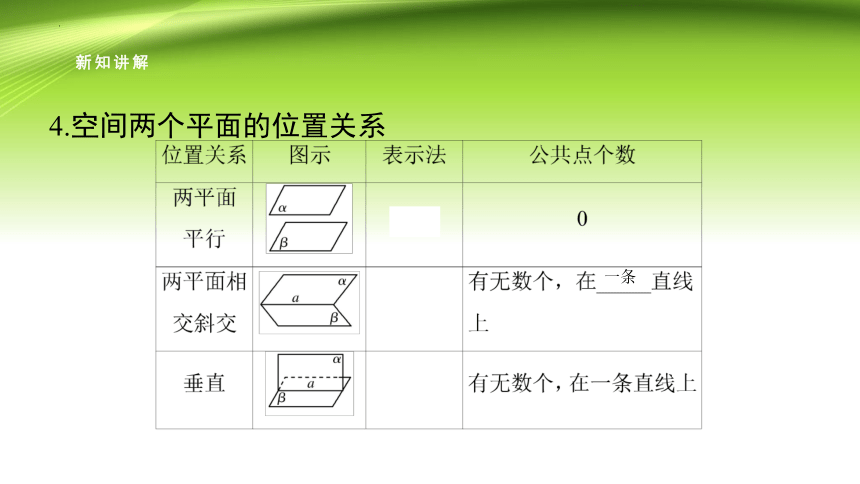
4.空间两个平面的位置关系
一条
新知讲解
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)没有公共点的两条直线一定是异面直线.( )
(2)两直线垂直,则这两条直线一定相交.( )
(3)两直线和第三条直线成等角,则这两条直线平行.( )
答案:(1)× (2)× (3)×
课堂练习
(4)若直线l平行于平面α内的无数条直线,则l∥α.( )
(5)若α∥β,a α,b β,则a与b是异面直线.( )
(6)若α∥β,a α,则a∥β.( )
(7)若α∩β=b,a α,则a与β一定相交.( )
答案:(1)× (2)× (3)√ (4)×
课堂练习
2.平面内一点与平面外一点连线和这个平面内直线的关系是__________.
答案:相交或异面
课堂练习
3. a,b,c是空间中的三条直线,下面给出五个命题:
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a∥c;课堂练习
③若a与b相交,b与c相交,则a与c相交;
④若a 平面α,b 平面β,则a,b一定是异面直线;
⑤若a,b与c成等角,则a∥b.
上述命题中正确的命题是________.(只填序号)
课堂练习
课堂练习
课堂练习
4.直线l与平面α有两个公共点,则( )
A.l∈α B.l∥α
C.l与α相交 D.l α
答案:D
课堂练习
5.正方体的六个面中互相平行的平面有( )
A.1对 B.2对
C.3对 D.4对
解析:如图,在正方体ABCD A1B1C1D1中,平面ABCD∥平面A1B1C1D1,平面ABB1A1∥平面CDD1C1,平面ADD1A1∥平面BCC1B1,故六个面中互相平行的平面有3对.
课堂练习
6.如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系是______________.
答案:平行或相交
课堂练习
课堂练习
7.(1)平面α内有无数条直线与平面β平行,问α∥β是否正确,为什么?
(2)平面α内的所有直线与平面β都平行,问α∥β是否正确,为什么?
课堂练习
解:(1)不正确.
如图所示,设α∩β=l,则在平面α内与l平行的直线可以有无数条:a1,a2,…,an,…,它们是一组平行线,这时a1,a2,…,an,…与平面β都平行(因为a1,a2,…,an,…与平面β无交点),但此时α与β不平行,α∩β=l.
(2)正确.
平面α内所有直线与平面β平行,则平面α与平面β无交点,符合平面与平面平行的定义.
课堂练习
1.空间两直线的位置关系有两种:共面和异面,而共面直线又包括相交直线和平行直线.异面直线和平行直线都没有公共点,区别是平行直线可以确定一个平面,而异面直线不同在任何一个平面内.
2.直线和平面的位置关系有直线在平面内和直线在平面外两种,而直线在平面外又包括直线和平面相交直线和平面平行.
3.平面和平面的位置关系有平行和相交两种,而相交又包括斜交和垂直.
4.研究线面关系时,利用正方体(或长方体、四面体)能有效地判定与两个平面的位置关系有关命题的真假
5.判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义,要有画图的意识,结合空间想象能力全方位、多角度地考虑问题,作出判断.
6.作两个平面的交线要注意直线的无限延伸和平面的无限延展,不要受所画图形的限制
课堂总结
作业布置
课本P131练习1-4
空间点、线、面之间位置关系
人教版高一年级第二册
教学目标
1. 会判断空间两直线间的位置关系.
2.会判断直线与平面、平面与平面的位置关系.
3.会判断平面与平面的位置关系.
4.会用符号语言和图形语言表示两直线、直线和平面、平面和平面的位置关系.
新知导入
1.空间中两条直线的位置关系
新知讲解
2.异面直线
(1)定义:把不同在_________平面内的两条直线叫做异面直线.
(2)画法:(通常用平面衬托)
任何一个
3.直线和平面的位置关系
无数
有且只有一
没有
新知讲解
4.空间两个平面的位置关系
一条
新知讲解
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)没有公共点的两条直线一定是异面直线.( )
(2)两直线垂直,则这两条直线一定相交.( )
(3)两直线和第三条直线成等角,则这两条直线平行.( )
答案:(1)× (2)× (3)×
课堂练习
(4)若直线l平行于平面α内的无数条直线,则l∥α.( )
(5)若α∥β,a α,b β,则a与b是异面直线.( )
(6)若α∥β,a α,则a∥β.( )
(7)若α∩β=b,a α,则a与β一定相交.( )
答案:(1)× (2)× (3)√ (4)×
课堂练习
2.平面内一点与平面外一点连线和这个平面内直线的关系是__________.
答案:相交或异面
课堂练习
3. a,b,c是空间中的三条直线,下面给出五个命题:
①若a∥b,b∥c,则a∥c;
②若a⊥b,b⊥c,则a∥c;课堂练习
③若a与b相交,b与c相交,则a与c相交;
④若a 平面α,b 平面β,则a,b一定是异面直线;
⑤若a,b与c成等角,则a∥b.
上述命题中正确的命题是________.(只填序号)
课堂练习
课堂练习
课堂练习
4.直线l与平面α有两个公共点,则( )
A.l∈α B.l∥α
C.l与α相交 D.l α
答案:D
课堂练习
5.正方体的六个面中互相平行的平面有( )
A.1对 B.2对
C.3对 D.4对
解析:如图,在正方体ABCD A1B1C1D1中,平面ABCD∥平面A1B1C1D1,平面ABB1A1∥平面CDD1C1,平面ADD1A1∥平面BCC1B1,故六个面中互相平行的平面有3对.
课堂练习
6.如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系是______________.
答案:平行或相交
课堂练习
课堂练习
7.(1)平面α内有无数条直线与平面β平行,问α∥β是否正确,为什么?
(2)平面α内的所有直线与平面β都平行,问α∥β是否正确,为什么?
课堂练习
解:(1)不正确.
如图所示,设α∩β=l,则在平面α内与l平行的直线可以有无数条:a1,a2,…,an,…,它们是一组平行线,这时a1,a2,…,an,…与平面β都平行(因为a1,a2,…,an,…与平面β无交点),但此时α与β不平行,α∩β=l.
(2)正确.
平面α内所有直线与平面β平行,则平面α与平面β无交点,符合平面与平面平行的定义.
课堂练习
1.空间两直线的位置关系有两种:共面和异面,而共面直线又包括相交直线和平行直线.异面直线和平行直线都没有公共点,区别是平行直线可以确定一个平面,而异面直线不同在任何一个平面内.
2.直线和平面的位置关系有直线在平面内和直线在平面外两种,而直线在平面外又包括直线和平面相交直线和平面平行.
3.平面和平面的位置关系有平行和相交两种,而相交又包括斜交和垂直.
4.研究线面关系时,利用正方体(或长方体、四面体)能有效地判定与两个平面的位置关系有关命题的真假
5.判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义,要有画图的意识,结合空间想象能力全方位、多角度地考虑问题,作出判断.
6.作两个平面的交线要注意直线的无限延伸和平面的无限延展,不要受所画图形的限制
课堂总结
作业布置
课本P131练习1-4
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
