圆的标准方程课件
图片预览











文档简介
课件33张PPT。生活中的圆生活剪影一石激起千层浪奥运五环福建土楼乐在其中小憩片刻4.1.1《圆的标准方程》 我们在前面学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.在平面直角坐标系中,如何确定一个圆呢?复习引入问题 当圆心位置与半径大小确定后,圆就唯一确定了.
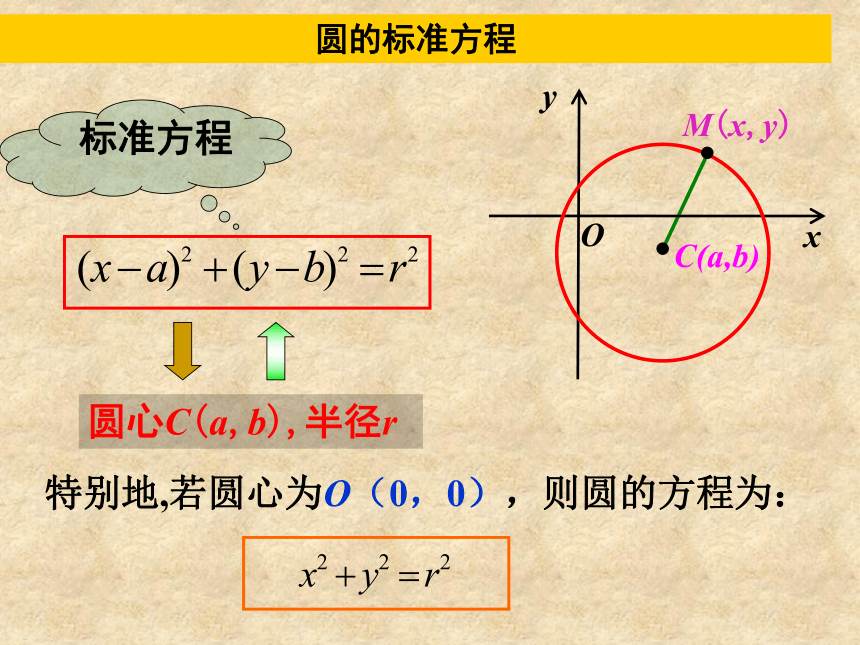
因此一个圆最基本要素是圆心和半径.引入新课 如图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离. 符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?符合上述条件的圆的集合:圆的方程问题 圆上任意点M(x, y)与圆心A (a,b)之间的距离能用什么公式表示?圆的方程根据两点间距离公式:则点M、A间的距离为:即: 是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?圆的标准方程 点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.问题 把这个方程称为圆心为A(a, b),半径长为r 的圆的方程,把它叫做圆的标准方程(standard equation of circle).特殊位置的圆方程 因为圆心是原点O(0, 0),将x=0,y=0和半径 r 带入圆的标准方程:问题 圆心在坐标原点,半径长为r 的圆的方程是什么? 得: 整理得:xyOC(a,b)M(x,y)圆心C(a,b),半径r特别地,若圆心为O(0,0),则圆的方程为:标准方程
圆的标准方程 例1 写出圆心为 ,半径长等于5的圆的方程. 解:圆心是 ,半径长等于5的圆的标准方程是:典型例题1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
(3)经过点P(5,1),圆心在点C(8,-3).2. 说出下列方程所表示的圆的圆心坐标和半径:(1) (x + 7)2 + ( y ? 4)2 = 36 (2) x2 + y2 ? 4x + 10y + 28 = 0 (3) (x ? a)2 + y 2 = m2 特殊位置的圆的方程: 圆心在原点: x2 + y2 = r2 (r≠0)圆心在x轴上: (x ? a)2 + y2 = r2 (r≠0) 圆心在y轴上: x2+ (y ? b)2 = r2 (r≠0) 圆过原点: (x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0) 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上. 解:圆心是 ,半径长等于5的圆的标准方程是: 把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;典型例题 把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上. 点M0(x0,y0)在圆(x-a)2+(y-b)2=r2上、内、外的条件是什么?探究点M0在圆上点M0在圆内点M0在圆外点与圆的位置关系 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程. 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解:设所求圆的方程是 (1) 因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是典型例题所以, 的外接圆的方程 .典型例题解此方程组,得: 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解: 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;
(2)列方程组;
(3)求系数;
(4)代入系数写出方程思: 还有其他解法吗? 圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyODA(5,1)B(7,-3)C(2,-8)例题分析例3、已知圆心为C的圆经过点A(1,1)和B(2,-2) 圆心C在直线l: x-y+1=0上,求圆心为C的圆的标准方程. 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1, 1)和B(2, -2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|. 解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标直线AB的斜率:典型例题因此线段AB的垂直平分线 的方程是即典型例题 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 解:所以圆心C的坐标是圆心为C的圆的半径长所以,圆心为C的圆的标准方程是典型例题解此方程组,得 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 解:例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.圆经过A(1,1),B(2,-2)解2:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法练习2、求出下列圆的方程(1) 圆心在(-1、2),与y轴相切(2)圆心在直线y=x上,与两轴同时相切,
半径为2. (3)已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.(2)圆心在直线y=x上,与两轴同时相切,半径为2.(3)已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.练习一般地,已知点A(x1,y1),B(x2,y2),则以线段AB为直径的圆方程如何? (x-x1)(x-x2)+(y-y1)(y-y2)=0知识小结圆的基本要素练习2.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6),且圆心在直线x-y+1=0上的圆的标准方程。
(2)圆心在直线5x-3y=8上,又与两坐标轴相切,求圆的方程。
(3)求以C(1,3)为圆心,且和直线3x-4y-7=0相切的直线的方程。1.点(2a, 1 ? a)在圆x2 + y2 = 4的内部,求实数 a 的取值范围.例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
解:
因此一个圆最基本要素是圆心和半径.引入新课 如图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径r的大小等于圆上任意点M(x, y)与圆心A (a,b) 的距离. 符合上述条件的圆的集合是什么?你能用描述法来表示这个集合吗?符合上述条件的圆的集合:圆的方程问题 圆上任意点M(x, y)与圆心A (a,b)之间的距离能用什么公式表示?圆的方程根据两点间距离公式:则点M、A间的距离为:即: 是否在圆上的点都适合这个方程?是否适合这个方程的坐标的点都在圆上?圆的标准方程 点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.问题 把这个方程称为圆心为A(a, b),半径长为r 的圆的方程,把它叫做圆的标准方程(standard equation of circle).特殊位置的圆方程 因为圆心是原点O(0, 0),将x=0,y=0和半径 r 带入圆的标准方程:问题 圆心在坐标原点,半径长为r 的圆的方程是什么? 得: 整理得:xyOC(a,b)M(x,y)圆心C(a,b),半径r特别地,若圆心为O(0,0),则圆的方程为:标准方程
圆的标准方程 例1 写出圆心为 ,半径长等于5的圆的方程. 解:圆心是 ,半径长等于5的圆的标准方程是:典型例题1.说出下列圆的方程:
(1) 圆心在原点,半径为3.
(2) 圆心在点C(3, -4), 半径为7.
(3)经过点P(5,1),圆心在点C(8,-3).2. 说出下列方程所表示的圆的圆心坐标和半径:(1) (x + 7)2 + ( y ? 4)2 = 36 (2) x2 + y2 ? 4x + 10y + 28 = 0 (3) (x ? a)2 + y 2 = m2 特殊位置的圆的方程: 圆心在原点: x2 + y2 = r2 (r≠0)圆心在x轴上: (x ? a)2 + y2 = r2 (r≠0) 圆心在y轴上: x2+ (y ? b)2 = r2 (r≠0) 圆过原点: (x ? a)2 + (y-b)2 = a2+b2 (a2+b2≠0) 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上. 解:圆心是 ,半径长等于5的圆的标准方程是: 把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;典型例题 把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上. 点M0(x0,y0)在圆(x-a)2+(y-b)2=r2上、内、外的条件是什么?探究点M0在圆上点M0在圆内点M0在圆外点与圆的位置关系 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程. 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解:设所求圆的方程是 (1) 因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是典型例题所以, 的外接圆的方程 .典型例题解此方程组,得: 分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆. 解: 例2 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;
(2)列方程组;
(3)求系数;
(4)代入系数写出方程思: 还有其他解法吗? 圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyODA(5,1)B(7,-3)C(2,-8)例题分析例3、已知圆心为C的圆经过点A(1,1)和B(2,-2) 圆心C在直线l: x-y+1=0上,求圆心为C的圆的标准方程. 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 分析:已知道确定一个圆只需要确定圆心的位置与半径大小.圆心为C的圆经过点A(1, 1)和B(2, -2),由于圆心C与A, B两点的距离相等,所以圆心C在线段AB的垂直平分线 上.又圆心C在直线l 上,因此圆心C是直线l与直线 的交点,半径长等于|CA|或|CB|. 解:因为A(1, 1)和B(2, -2),所以线段AB的中点D的坐标直线AB的斜率:典型例题因此线段AB的垂直平分线 的方程是即典型例题 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 解:所以圆心C的坐标是圆心为C的圆的半径长所以,圆心为C的圆的标准方程是典型例题解此方程组,得 例3 已知圆心为C的圆经过点A(1, 1)和B(2, -2),且圆心C在直线上l:x - y+1=0,求圆心为C的圆的标准方程. 解:例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.圆经过A(1,1),B(2,-2)解2:设圆C的方程为∵圆心在直线l:x-y+1=0上待定系数法练习2、求出下列圆的方程(1) 圆心在(-1、2),与y轴相切(2)圆心在直线y=x上,与两轴同时相切,
半径为2. (3)已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.(2)圆心在直线y=x上,与两轴同时相切,半径为2.(3)已知两点A(4、9)、B(6、 3), 求以AB为直径的圆的方程.练习一般地,已知点A(x1,y1),B(x2,y2),则以线段AB为直径的圆方程如何? (x-x1)(x-x2)+(y-y1)(y-y2)=0知识小结圆的基本要素练习2.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6),且圆心在直线x-y+1=0上的圆的标准方程。
(2)圆心在直线5x-3y=8上,又与两坐标轴相切,求圆的方程。
(3)求以C(1,3)为圆心,且和直线3x-4y-7=0相切的直线的方程。1.点(2a, 1 ? a)在圆x2 + y2 = 4的内部,求实数 a 的取值范围.例 已知圆的方程是x2 + y2 = r2,求经过圆上一 点 的切线的方程。
解:
