5.2 反比例函数(2) 初中数学青岛版九年级下册 同步课件(共22张PPT)
文档属性
| 名称 | 5.2 反比例函数(2) 初中数学青岛版九年级下册 同步课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 18:14:33 | ||
图片预览








文档简介
(共22张PPT)
5.2 反比例函数(2)
1.会画反例函数的图象;
2.能根据图象和表达式探索并理解反比例函数的性质。
学习目标
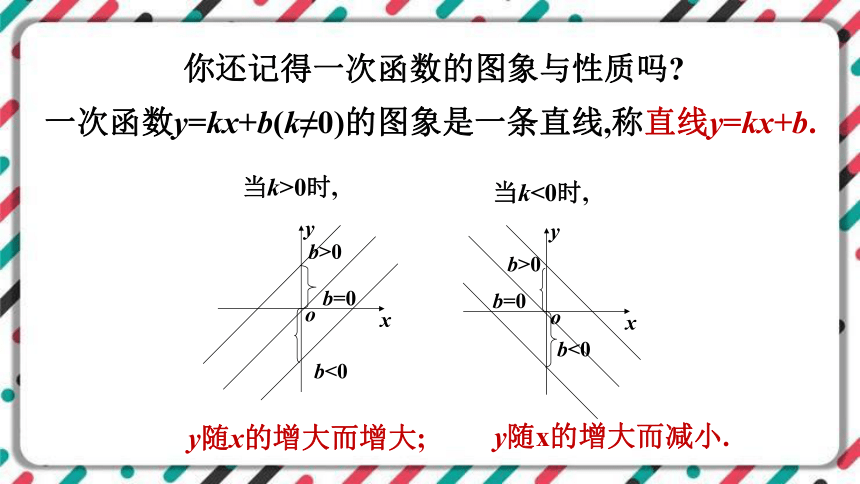
你还记得一次函数的图象与性质吗
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
x
y
o
x
y
o
y随x的增大而减小.
b<0
b>0
b=0
b<0
b>0
b=0
当k>0时,
当k<0时,
实验与探究
(1)反比例函数 的自变量x可以取值的范围是什么
(2)为了画出 的图象,需要先列表.列表时,应选取哪些自变量的值呢
(3)在x≠0的范围内,选定x的下列值,计算出对应的y值,完成下面的表格:
x -8 -6 -4 -2 -1 1 2 4 6 8
y
注意:①必须在自变量可以取值的范国内选取x的值.
②所取的x的值应有利予计算对应的y值和描点。还要能整体地反快出函数的图象.
实验与探究
实验与探究
(4)以表中每对x,y的值作为点的坐标,在直角坐标系中描出对应的点(图5-8).
实验与探究
(5) 连线时,所描出的相邻两点如 A(2,4)与B(4,2)之间,能不能用线段来连接 为什么 如果不能,应当如何连接
在2因为线段AB的表达式为y=-x +6,如果将x=3代人该式,得y=3.由 <3,可知点C在线段AB的下方.
实验与探究
然后再分别在2类似地可以判断,当x>0时在其他描出的相邻的各点中,函数 的图象上的各点都分别在以它们为端点的线段的下方,因此连线时要用向下凹的平滑曲线连接描出的各点.而当x< 0时,情况相反连线时要用向上凸的平滑曲线连接描出的各点.
实验与探究
(6)想一想,在图 5-8 中能用线段或平滑的曲线将点 (-1,-8)与点(1,8) 连接吗 为什么
实验与探究
(7)用平滑的曲线按自变量由小到大的顺序顺次连接在图 5-8 中点,便画出函数 的图象(图5-9 ).
实验与探究
(8)你能用上面的方法画出反比例函数 的图象吗 试一试 (图5-10 ).
实验与探究
类似地,可以画出反比例函数 和 的图象(图5-11①、②).
观察与思考
(1)类比利用一次函数的图象研究其性质的过程,你认为可以通过观察图象(图5-9、图5-10、图 5-11)的哪些特征认识反比例函数的性质
观察与思考
(2)观察函数 与 以及 与 的图象,你发现它们的形状、位置有哪些共同特征和不同点
它们的形状基本相同,都由两支曲线组成;图象都不经过原点;并且与两坐标轴都不相交.但它们在坐标系中的位置不同, 和 的图象在第一和三象限, 和
的图象在第二、四象限.
反比例函数的性质
1. 当k>0时, 图象的两个分支分别在第一、三象限内。在每个象限内,y随x的增大而减小.
2. 当k<0时, 图象的两个分支分别在第二、四象限内。在每个象限内, y随x的增大而增大.
挑战自我
(1)已知P (x ,y ),P ,(x ,y ),P ;(x ;,y ),P (x ,y ) 是反比例函数 上的四个点,且x如何比较y ,y ,y ,y 的大小关系
方法一.特殊值法
不妨设: 代入
得,
挑战自我
方法二.分析法
因为k=-3<0,根据性质可知图象的两个分支分别在第二、四象限内,并且在每个象限内,y随x的增大而增大,在第二象限内的函数值为正的,第四象限的函数值为负的。
挑战自我
方法三.图像法
挑战自我
解析:显然将P1,P2分别代入各自双曲线得,
k1=2b1,k2=2b2,因b1所以: k1 < k2
挑战自我
(2)已知点P (2,b ,), P ,(2,b ,)分别在双曲线 和 上,如果b ,< b ,如何比较k ,k ,的大小关系
一、反比例函数 有下列性质:
1.反比例函数的图象 是由两支曲线组成的。
因此,称反比例函数的图象为双曲线.
2.(1)当 k>0 时,两支曲线分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
总结
(2)当 k<0 时,两支曲线分别位于第二、四象限,在每个象限内,y随x的增大而增大.
二、函数值大小的比较方法
总结
5.2 反比例函数(2)
1.会画反例函数的图象;
2.能根据图象和表达式探索并理解反比例函数的性质。
学习目标
你还记得一次函数的图象与性质吗
一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.
y随x的增大而增大;
x
y
o
x
y
o
y随x的增大而减小.
b<0
b>0
b=0
b<0
b>0
b=0
当k>0时,
当k<0时,
实验与探究
(1)反比例函数 的自变量x可以取值的范围是什么
(2)为了画出 的图象,需要先列表.列表时,应选取哪些自变量的值呢
(3)在x≠0的范围内,选定x的下列值,计算出对应的y值,完成下面的表格:
x -8 -6 -4 -2 -1 1 2 4 6 8
y
注意:①必须在自变量可以取值的范国内选取x的值.
②所取的x的值应有利予计算对应的y值和描点。还要能整体地反快出函数的图象.
实验与探究
实验与探究
(4)以表中每对x,y的值作为点的坐标,在直角坐标系中描出对应的点(图5-8).
实验与探究
(5) 连线时,所描出的相邻两点如 A(2,4)与B(4,2)之间,能不能用线段来连接 为什么 如果不能,应当如何连接
在2
实验与探究
然后再分别在2
实验与探究
(6)想一想,在图 5-8 中能用线段或平滑的曲线将点 (-1,-8)与点(1,8) 连接吗 为什么
实验与探究
(7)用平滑的曲线按自变量由小到大的顺序顺次连接在图 5-8 中点,便画出函数 的图象(图5-9 ).
实验与探究
(8)你能用上面的方法画出反比例函数 的图象吗 试一试 (图5-10 ).
实验与探究
类似地,可以画出反比例函数 和 的图象(图5-11①、②).
观察与思考
(1)类比利用一次函数的图象研究其性质的过程,你认为可以通过观察图象(图5-9、图5-10、图 5-11)的哪些特征认识反比例函数的性质
观察与思考
(2)观察函数 与 以及 与 的图象,你发现它们的形状、位置有哪些共同特征和不同点
它们的形状基本相同,都由两支曲线组成;图象都不经过原点;并且与两坐标轴都不相交.但它们在坐标系中的位置不同, 和 的图象在第一和三象限, 和
的图象在第二、四象限.
反比例函数的性质
1. 当k>0时, 图象的两个分支分别在第一、三象限内。在每个象限内,y随x的增大而减小.
2. 当k<0时, 图象的两个分支分别在第二、四象限内。在每个象限内, y随x的增大而增大.
挑战自我
(1)已知P (x ,y ),P ,(x ,y ),P ;(x ;,y ),P (x ,y ) 是反比例函数 上的四个点,且x
方法一.特殊值法
不妨设: 代入
得,
挑战自我
方法二.分析法
因为k=-3<0,根据性质可知图象的两个分支分别在第二、四象限内,并且在每个象限内,y随x的增大而增大,在第二象限内的函数值为正的,第四象限的函数值为负的。
挑战自我
方法三.图像法
挑战自我
解析:显然将P1,P2分别代入各自双曲线得,
k1=2b1,k2=2b2,因b1
挑战自我
(2)已知点P (2,b ,), P ,(2,b ,)分别在双曲线 和 上,如果b ,< b ,如何比较k ,k ,的大小关系
一、反比例函数 有下列性质:
1.反比例函数的图象 是由两支曲线组成的。
因此,称反比例函数的图象为双曲线.
2.(1)当 k>0 时,两支曲线分别位于第一、三象限,
在每个象限内,y随x的增大而减小.
总结
(2)当 k<0 时,两支曲线分别位于第二、四象限,在每个象限内,y随x的增大而增大.
二、函数值大小的比较方法
总结
