5.2 反比例函数 初中数学青岛版九年级下册 同步课件(2课时、共21张PPT)
文档属性
| 名称 | 5.2 反比例函数 初中数学青岛版九年级下册 同步课件(2课时、共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 18:16:19 | ||
图片预览







文档简介
(共21张PPT)
5.2 反比例函数
第三课时
1.理解反比例函数中k的几何性质;
2.能综合运用反比例函数的知识解决相关问题.
学习目标
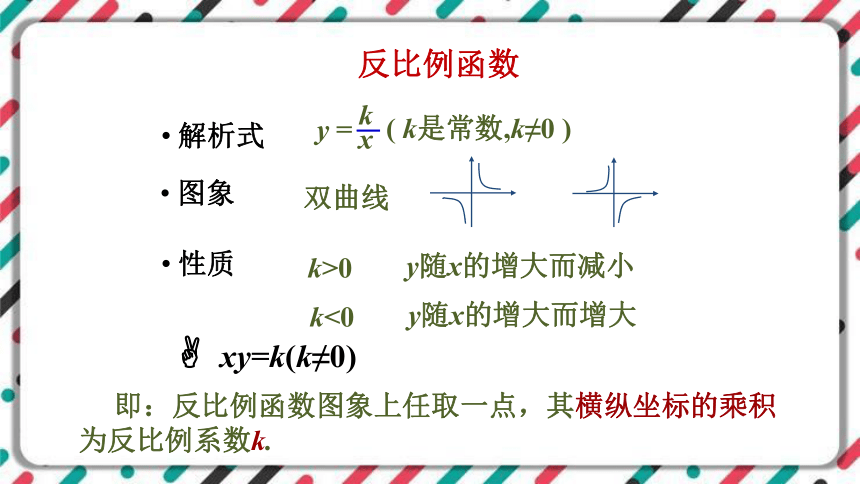
反比例函数
( k是常数,k≠0 )
y =
x
k
解析式
图象
性质
双曲线
k>0
y随x的增大而减小
k<0
y随x的增大而增大
xy=k(k≠0)
即:反比例函数图象上任取一点,其横纵坐标的乘积为反比例系数k.
P
Q
S1
S2
想一想:S1、S2有什么关系?为什么?
R
S3
结论:任取一点向两坐标轴作垂线得到的矩形面积是一个定值,为|k |.
观察思考
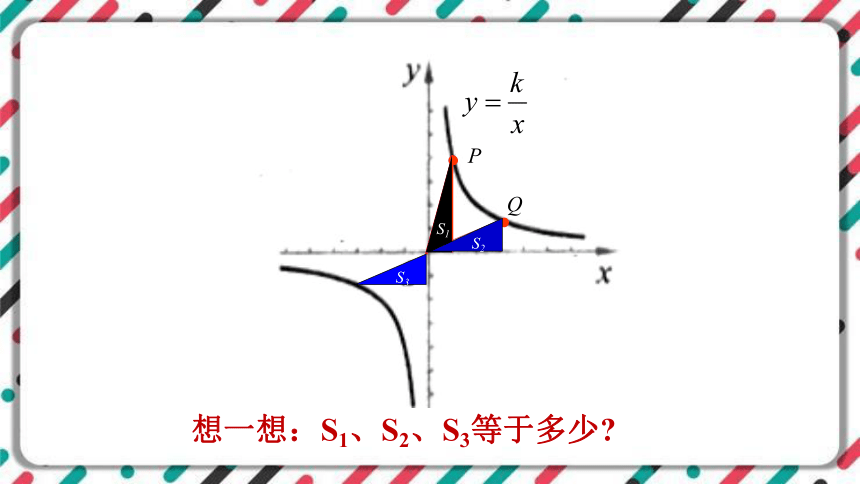
P
Q
想一想:S1、S2、S3等于多少
S1
S2
S3
如图5-12,已知点C,P的坐标分别为(2,y)和(x, ),这两点在反比例函数
的图象上过点C,P作x轴的垂线,垂足分别为点A,Q.过点 C,P作y轴的垂线,垂足分别为点B,R.
例3
(1)矩形OACB与矩形OCPR的面积分别是多少
(2)设 CA与PR交于点D,求矩形OACB与矩形OQPR公共部分的面积.
解析:(1)由反比例函数的几何性质可知:
(2)点D的横坐标等于点 C的横坐标2,即DR =2,点D的纵坐标等于点P的纵坐标 ,即DA = .
所以,矩形 OACB 与矩形 OQPR 的公共部分即矩形 OADR 的面积为2× = .
解:
因为A(-2,3)在函数 的图象上,所以3= ,k=-6.
如图5-13,已知反比例函数 的图象与直线y=ax +b相交于点A(-2,3),B(3,m).求k及a,b的值.
例4
又因为B(3,m)在函数 图象上,所以m= = -2,因此点B的坐标为(3,-2).
将A(-2,3),B(3,-2) 分别代入y=ax +b,
得 3 =-2a +b,
-2=3a+b,
解这个二元一次方程组,
得 a = -1,
b =1.
例4
挑战自我
在同一个直角坐标系中反比例函数 与
(k ≠k )的图象能相交吗 说明理由.
解析:不能相交;假设相交于点A(a,b),
则应有ab=k1=k2,这与k1≠k2相矛盾.
所以不能相交.
一、反比例函数中k的几何性质
反比例函数图象上任取一点,向两坐标轴作垂线,得到的矩形面积是一个定值,为|k |.
二、反比例函数综合运基本思路
首先运用待定系数法求出相关的函数关系式;
再根据要求运用函数性质解决问题.
注意: 任意两个反比例函数的图象均不相交.
总结
5.2 反比例函数(4)
1.能根据实际问题中的条件确定反比例函数的解析式;
2.能综合利用反比例函数的知识分析和解决一些简单的实际问题.
学习目标
解:(1)由已知,可求出从甲地到乙地的路程为S=80×5 = 400 (km ).
由vt = 400及限速条件,可得t与v之间函数的表达式为t= ,0其图象为双曲线t= 在第一限内的一段(图5-14).
一位汽车以80km/h的平均速度从甲地去乙地,用5小时到达,然后按原路返回.
(1)如果规定该车限速120km/h,写出返回甲地所用的时间t与平均速度v的函数表达式,并画出它的图象;
例5
(2)如果汽车必须在4个小时内回到甲地,则返程时平均速度的范围?
解:(2)当t=4时,
v = = 100 ( km/h )
所以,如果汽车必须在 4 h内回到甲地,那么100 ≤v ≤ 120,即返程时平均速度的范围不低于 100 km/h、不大于 120 km/h.
某校对教室采用药薰法进行灭蚊.根据药品使用说明,药物燃烧时,室内每立方米空气中含药量y(mg/m )与药物点燃后的时间x(min)成正比例,药物燃尽后,y与x成反比例(图5-15).
已知药物点燃后8 min燃尽,
此时室内每立方米空气中含药量
为6mg.
例6
(1)药物燃烧时,求y与x的关系式;
例6
解析: (1)当药物燃烧时,y是x的正比例函数,
设它的表达式为 ( 0≤x≤8 )
把分段点(8,6)代入上式,得6=8k ,解得:
所以,药物燃烧时,y与x之前的函数表达式为
(2)药物燃烧完后,求y与x的关系式;
例6
将分段点(8,6)代入上式,得 ,解得k =48
所以,药物燃尽后,y与x之间函数的表达式为
(2)当药物燃尽后,y是x的反比例函数,设它的表达式是
(3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于1.6 mg时,对人体是安全的,那么从开始药薰,至少经过多少时间,学生才能进入教室?
解:(3)将y=1.6代入
所以,从灭蚊开始至少需经过30min,学生才能进入教室.
1.6
30
例6
3
(4)根据火敏药品使用说明,当每立方米空气中含药量不低于3mg且持续时间不低于10min时才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效 为什么
(4)把y=3代入两函数得
4
16
因此,从药物点燃4min到16min时室内每立方米空气中含药量超过3mg;由于x -x =16-4=12(min)>10(min),所以此次灭蚊有效.
例6
实际问题 数学问题(反比例函数)
1.本节课学习的数学知识:运用反比例函数的知识解决实际问题.
2.本节课学习的数学方法:建模思想和函数的思想.
转化
解决
反思:
1.本节课你有什么收获?
2.你对自己今天的表现满意吗?
总结
5.2 反比例函数
第三课时
1.理解反比例函数中k的几何性质;
2.能综合运用反比例函数的知识解决相关问题.
学习目标
反比例函数
( k是常数,k≠0 )
y =
x
k
解析式
图象
性质
双曲线
k>0
y随x的增大而减小
k<0
y随x的增大而增大
xy=k(k≠0)
即:反比例函数图象上任取一点,其横纵坐标的乘积为反比例系数k.
P
Q
S1
S2
想一想:S1、S2有什么关系?为什么?
R
S3
结论:任取一点向两坐标轴作垂线得到的矩形面积是一个定值,为|k |.
观察思考
P
Q
想一想:S1、S2、S3等于多少
S1
S2
S3
如图5-12,已知点C,P的坐标分别为(2,y)和(x, ),这两点在反比例函数
的图象上过点C,P作x轴的垂线,垂足分别为点A,Q.过点 C,P作y轴的垂线,垂足分别为点B,R.
例3
(1)矩形OACB与矩形OCPR的面积分别是多少
(2)设 CA与PR交于点D,求矩形OACB与矩形OQPR公共部分的面积.
解析:(1)由反比例函数的几何性质可知:
(2)点D的横坐标等于点 C的横坐标2,即DR =2,点D的纵坐标等于点P的纵坐标 ,即DA = .
所以,矩形 OACB 与矩形 OQPR 的公共部分即矩形 OADR 的面积为2× = .
解:
因为A(-2,3)在函数 的图象上,所以3= ,k=-6.
如图5-13,已知反比例函数 的图象与直线y=ax +b相交于点A(-2,3),B(3,m).求k及a,b的值.
例4
又因为B(3,m)在函数 图象上,所以m= = -2,因此点B的坐标为(3,-2).
将A(-2,3),B(3,-2) 分别代入y=ax +b,
得 3 =-2a +b,
-2=3a+b,
解这个二元一次方程组,
得 a = -1,
b =1.
例4
挑战自我
在同一个直角坐标系中反比例函数 与
(k ≠k )的图象能相交吗 说明理由.
解析:不能相交;假设相交于点A(a,b),
则应有ab=k1=k2,这与k1≠k2相矛盾.
所以不能相交.
一、反比例函数中k的几何性质
反比例函数图象上任取一点,向两坐标轴作垂线,得到的矩形面积是一个定值,为|k |.
二、反比例函数综合运基本思路
首先运用待定系数法求出相关的函数关系式;
再根据要求运用函数性质解决问题.
注意: 任意两个反比例函数的图象均不相交.
总结
5.2 反比例函数(4)
1.能根据实际问题中的条件确定反比例函数的解析式;
2.能综合利用反比例函数的知识分析和解决一些简单的实际问题.
学习目标
解:(1)由已知,可求出从甲地到乙地的路程为S=80×5 = 400 (km ).
由vt = 400及限速条件,可得t与v之间函数的表达式为t= ,0
一位汽车以80km/h的平均速度从甲地去乙地,用5小时到达,然后按原路返回.
(1)如果规定该车限速120km/h,写出返回甲地所用的时间t与平均速度v的函数表达式,并画出它的图象;
例5
(2)如果汽车必须在4个小时内回到甲地,则返程时平均速度的范围?
解:(2)当t=4时,
v = = 100 ( km/h )
所以,如果汽车必须在 4 h内回到甲地,那么100 ≤v ≤ 120,即返程时平均速度的范围不低于 100 km/h、不大于 120 km/h.
某校对教室采用药薰法进行灭蚊.根据药品使用说明,药物燃烧时,室内每立方米空气中含药量y(mg/m )与药物点燃后的时间x(min)成正比例,药物燃尽后,y与x成反比例(图5-15).
已知药物点燃后8 min燃尽,
此时室内每立方米空气中含药量
为6mg.
例6
(1)药物燃烧时,求y与x的关系式;
例6
解析: (1)当药物燃烧时,y是x的正比例函数,
设它的表达式为 ( 0≤x≤8 )
把分段点(8,6)代入上式,得6=8k ,解得:
所以,药物燃烧时,y与x之前的函数表达式为
(2)药物燃烧完后,求y与x的关系式;
例6
将分段点(8,6)代入上式,得 ,解得k =48
所以,药物燃尽后,y与x之间函数的表达式为
(2)当药物燃尽后,y是x的反比例函数,设它的表达式是
(3)根据灭蚊药品使用说明,当空气中每立方米的含药量低于1.6 mg时,对人体是安全的,那么从开始药薰,至少经过多少时间,学生才能进入教室?
解:(3)将y=1.6代入
所以,从灭蚊开始至少需经过30min,学生才能进入教室.
1.6
30
例6
3
(4)根据火敏药品使用说明,当每立方米空气中含药量不低于3mg且持续时间不低于10min时才能有效杀灭室内的蚊虫,那么此次灭蚊是否有效 为什么
(4)把y=3代入两函数得
4
16
因此,从药物点燃4min到16min时室内每立方米空气中含药量超过3mg;由于x -x =16-4=12(min)>10(min),所以此次灭蚊有效.
例6
实际问题 数学问题(反比例函数)
1.本节课学习的数学知识:运用反比例函数的知识解决实际问题.
2.本节课学习的数学方法:建模思想和函数的思想.
转化
解决
反思:
1.本节课你有什么收获?
2.你对自己今天的表现满意吗?
总结
