6.6 简单的概率计算 初中数学青岛版九年级下册 同步课件(2课时、共21张PPT)
文档属性
| 名称 | 6.6 简单的概率计算 初中数学青岛版九年级下册 同步课件(2课时、共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 18:25:51 | ||
图片预览








文档简介
(共21张PPT)
6.6 简单的概率计算
第二课时
学会使用概率计算公式计算简单随机事件发生的概率.
学习目标
一般地,在一次试验中,如果共有有限个可能发生的结果,并且每种结果发生的可能性都相等,用m表示一个指定事件E包含的结果数,n表示试验可能出现的所有结果的总数,那么事件E发生的概率可利用下面的公式计算:
回顾
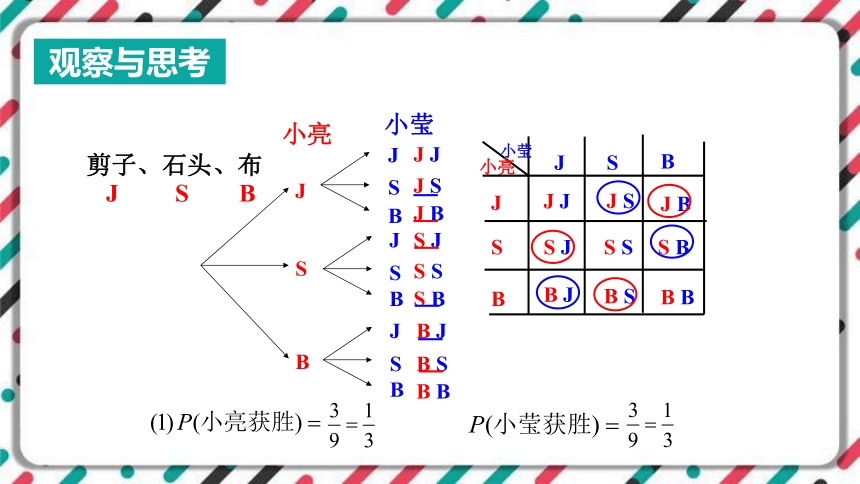
你玩过剪子、石头、布的游戏吗?
小亮和小莹玩这个游戏,游戏规则是:
“剪刀”胜“布”
“布” 胜“石头”
“石头”胜“剪刀”
(1)如果二人都随机出一个手势,那么在第一次“出手”时,小亮获胜的概率有多大?小莹获胜的概率呢?
观察与思考
剪子、石头、布
J S B
J
S
B
小亮
小莹
J
S
B
J
S
B
J
S
B
J J
J S
J B
S J
S S
S B
B J
B S
B B
小亮
小莹
J
S
B
J
S
B
J J
J S
J B
S J
S B
B J
B S
B B
S S
观察与思考
(2)两人同时出手后,出现平局的概率有多大?
(3)假设两人 经过n此出手,皆为平局,直到第n+1次出手实验才决出胜负,那么在第n+1次出手时,甲、乙两人获胜的概率分别为多大?
观察与思考
某快餐店为了招揽顾客,推出一种“转盘”游戏:一个圆形转盘被分成了12个圆心角都相等的扇形,其中有2个扇形涂成红色,4个扇形涂成绿色,其余涂成黄色。顾客消费满200元后,可以自由转动一次转盘。如果转盘停止后,指针落在绿色区域获得二等奖,落在红色区域
获得一等奖,凭奖券顾客下次来店就餐时,
可分别享受九折、八折优惠。
例3
(1)这个游戏一、二等奖的中奖率分别是多少?
(2)这个游戏的中奖率是多少?
例3
分析:指针落在转盘的位置实际上有无限多个等可能的结果,将转盘等分为若干扇形后,就转化为只有有限多个等可能结果的情况,从而可以利用上节课的公式来计算概率。
你知道田忌赛马的故事吗?据《史记》记载,在战国时期,齐威王和他的大臣田忌各有上、中、下三匹马,在同等级的马中,齐威王的马比田忌的马跑得快,但每人较高等级的马都比对方较低等级的马跑的快。有一天齐威王要与田忌赛马,双方约定:比赛两局,每局各出一匹,每匹马只赛一次,赢得两局着为胜。齐威王的马按上、中、下顺序出阵,加入田忌的马随机出阵,田忌获胜的概率是多少?
例3
齐:
上
中
下
田:
上
中
下
上
下
中
中
上
下
中
下
上
下
上
中
下
中
上
√
X
X
X
X
X
X
√
X
X
X
√
X
√
√
X
X
√
例3
1.从正面分别写有1、2、3、4、5、6的6张卡片中,任意抽出1张,得到下列结果的概率是多少?
(1)卡片上的数字是奇数;
(2)卡片上的数字是偶数;
(3)卡片上的数字不小于3.
练习
2.个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色外没有任何区别,现从中任意摸出一个球。
(1)计算摸到的是绿球的概率。
(2)如果要使摸到绿球的概率为1/4,需要 在口袋中再放入多少个绿球?
练习
通过今天的学习,你对概率的简单计算有什么收获和新的认识?能谈谈你的想法吗?
6.6 简单的概率计算(3)
1.通过实例进一步丰富对概率的认识;
2.会用几何的方法求简单的概率;
3.紧密结合实际,培养应用数学的意识.
学习目标
2路车公交车站每隔5分钟发一班车.小亮来到这个汽车站,问候车时间不超过1分钟的概率是多少?候车时间等于或超过3分钟的概率是多少?
解:
画一条长度为5个单位的线段,表示相邻两次发车的间隔时间.用左端点表示上一班车开走的时刻,记为0 min,右端点表示下一班车开走的时刻,记为5min.
5
4
1
0
3
2
例5
由于车站每隔5分钟发一班车,当到达车站在最后1分钟内时,候车时间不超过1分钟,于是
当上一班汽车发车2分钟以内(包括2分钟)到达汽车站时,候车时间等于或超过3分钟.
5
2
3
(
=
≥
分钟)
候车时间
P
例5
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
例6
画一条长度为2.5单位的线段AB,表示从绿灯开启到红灯关闭的间隔时间在AB上取点C,使AC=1.5单位(图6-16),表示绿灯开启的时间段汽车到达十字路口的时刻是随机的,它出现在每一时刻的概率是相等的,把这一时刻看作一个点,该点落在线段AC上的概率是P(点落在AC)
例6
解:这个十字路口从绿灯开启到红灯关闭(同时下一次绿灯开启)共2.5min,其中绿灯1.5min,红灯1min.
P(遇到绿灯)
A
C
D
例6
区域长度(面积)
事件
概率
长度(面积)比
数量
数量比
事件A发生的可能的结果数
所有可能的结果总数
P(A)=
总结
6.6 简单的概率计算
第二课时
学会使用概率计算公式计算简单随机事件发生的概率.
学习目标
一般地,在一次试验中,如果共有有限个可能发生的结果,并且每种结果发生的可能性都相等,用m表示一个指定事件E包含的结果数,n表示试验可能出现的所有结果的总数,那么事件E发生的概率可利用下面的公式计算:
回顾
你玩过剪子、石头、布的游戏吗?
小亮和小莹玩这个游戏,游戏规则是:
“剪刀”胜“布”
“布” 胜“石头”
“石头”胜“剪刀”
(1)如果二人都随机出一个手势,那么在第一次“出手”时,小亮获胜的概率有多大?小莹获胜的概率呢?
观察与思考
剪子、石头、布
J S B
J
S
B
小亮
小莹
J
S
B
J
S
B
J
S
B
J J
J S
J B
S J
S S
S B
B J
B S
B B
小亮
小莹
J
S
B
J
S
B
J J
J S
J B
S J
S B
B J
B S
B B
S S
观察与思考
(2)两人同时出手后,出现平局的概率有多大?
(3)假设两人 经过n此出手,皆为平局,直到第n+1次出手实验才决出胜负,那么在第n+1次出手时,甲、乙两人获胜的概率分别为多大?
观察与思考
某快餐店为了招揽顾客,推出一种“转盘”游戏:一个圆形转盘被分成了12个圆心角都相等的扇形,其中有2个扇形涂成红色,4个扇形涂成绿色,其余涂成黄色。顾客消费满200元后,可以自由转动一次转盘。如果转盘停止后,指针落在绿色区域获得二等奖,落在红色区域
获得一等奖,凭奖券顾客下次来店就餐时,
可分别享受九折、八折优惠。
例3
(1)这个游戏一、二等奖的中奖率分别是多少?
(2)这个游戏的中奖率是多少?
例3
分析:指针落在转盘的位置实际上有无限多个等可能的结果,将转盘等分为若干扇形后,就转化为只有有限多个等可能结果的情况,从而可以利用上节课的公式来计算概率。
你知道田忌赛马的故事吗?据《史记》记载,在战国时期,齐威王和他的大臣田忌各有上、中、下三匹马,在同等级的马中,齐威王的马比田忌的马跑得快,但每人较高等级的马都比对方较低等级的马跑的快。有一天齐威王要与田忌赛马,双方约定:比赛两局,每局各出一匹,每匹马只赛一次,赢得两局着为胜。齐威王的马按上、中、下顺序出阵,加入田忌的马随机出阵,田忌获胜的概率是多少?
例3
齐:
上
中
下
田:
上
中
下
上
下
中
中
上
下
中
下
上
下
上
中
下
中
上
√
X
X
X
X
X
X
√
X
X
X
√
X
√
√
X
X
√
例3
1.从正面分别写有1、2、3、4、5、6的6张卡片中,任意抽出1张,得到下列结果的概率是多少?
(1)卡片上的数字是奇数;
(2)卡片上的数字是偶数;
(3)卡片上的数字不小于3.
练习
2.个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色外没有任何区别,现从中任意摸出一个球。
(1)计算摸到的是绿球的概率。
(2)如果要使摸到绿球的概率为1/4,需要 在口袋中再放入多少个绿球?
练习
通过今天的学习,你对概率的简单计算有什么收获和新的认识?能谈谈你的想法吗?
6.6 简单的概率计算(3)
1.通过实例进一步丰富对概率的认识;
2.会用几何的方法求简单的概率;
3.紧密结合实际,培养应用数学的意识.
学习目标
2路车公交车站每隔5分钟发一班车.小亮来到这个汽车站,问候车时间不超过1分钟的概率是多少?候车时间等于或超过3分钟的概率是多少?
解:
画一条长度为5个单位的线段,表示相邻两次发车的间隔时间.用左端点表示上一班车开走的时刻,记为0 min,右端点表示下一班车开走的时刻,记为5min.
5
4
1
0
3
2
例5
由于车站每隔5分钟发一班车,当到达车站在最后1分钟内时,候车时间不超过1分钟,于是
当上一班汽车发车2分钟以内(包括2分钟)到达汽车站时,候车时间等于或超过3分钟.
5
2
3
(
=
≥
分钟)
候车时间
P
例5
单击此处编辑母版文本样式
第二级
第三级
第四级
第五级
例6
画一条长度为2.5单位的线段AB,表示从绿灯开启到红灯关闭的间隔时间在AB上取点C,使AC=1.5单位(图6-16),表示绿灯开启的时间段汽车到达十字路口的时刻是随机的,它出现在每一时刻的概率是相等的,把这一时刻看作一个点,该点落在线段AC上的概率是P(点落在AC)
例6
解:这个十字路口从绿灯开启到红灯关闭(同时下一次绿灯开启)共2.5min,其中绿灯1.5min,红灯1min.
P(遇到绿灯)
A
C
D
例6
区域长度(面积)
事件
概率
长度(面积)比
数量
数量比
事件A发生的可能的结果数
所有可能的结果总数
P(A)=
总结
