沪科版七年级下册10.2 平行线的判定 课件(共54张PPT)
文档属性
| 名称 | 沪科版七年级下册10.2 平行线的判定 课件(共54张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 19:32:50 | ||
图片预览










文档简介
(共54张PPT)
10.2 平行线的判定
第十章 相交线、平行线与平移
学习目标
课时讲解
1
平行线的定义及画法
基本事实及其推论
同位角、内错角、同旁内角
平行线的判定的基本事实
平行线的判定方法 2
平行线的判定方法 3
平行线判定方法的推论
逐点
导讲练
课堂小结
作业提升
学习目标
课时流程
2
知识点
平行线的定义及画法
感悟新知
1
1. 定义 在同一平面内不相交的两条直线叫做平行线.
特别提醒:平行线的定义三要素:
(1)在同一平面内;
(2)不相交;
(3)都是直线.
感悟新知
2. 表示方法:用“∥”表示平行,如图10.2-1,记作“AB ∥ CD”或“CD ∥ AB ” ,读作“AB 平行于CD ”或“CD 平行于AB ”.
感悟新知
特别解读
1. 在同一平面内,不重合的两条直线的位置关系: ●相交; ●平行.
2. 经过直线上一点不可以作已知直线的平行线 .
3. 画线段或射线的平行线是画它们所在直线的平行线 .
感悟新知
读下列语句,并画出图形 . 直线 AB, CD 是两条直
线, P 是直线 AB, CD 外的一点,直线 EF 经过点 P 与 AB 平行,直线 MN 经过点 P 与 CD 垂直 .
例 1
感悟新知
解题秘方:按照语句的要求,结合平行线的画法进行作图 .
解法提醒
根据语句画图时,要注意画出的图形符合语句的要求,若语句中没有说清楚的,要考虑各种情况,如本题中AB,CD 之间没有指明位置关系,所以画图时可以平行也可以相交 .
感悟新知
解:如图 10.2-2 所示 .
知识点
基本事实及其推论
感悟新知
2
1. 基本事实 经过直线外一点,有且只有一条直线平行于这条直线.
特别提醒:基本事实的前提是经过直线外一点,若点在直线上,则不可能有平行线.
特别解读
“有且只有”强调这样的直线的存在性和唯一性.
感悟新知
2. 推论 如果两条直线都和第三条直线平行,那么这两条直线平行.
简称:平行于第三条直线的两条直线平行.
表达方式:如果a ∥ c,b ∥ c,那么a ∥ b.
感悟新知
如图10.2-3,直线a ∥ b,b ∥ c,d 与a 相交于点M.
(1)试判断直线a,c 的位置关系,并说明理由;
(2)判断c 与d 的位置关系,并说明理由.
解题秘方:根据平行公理及其推论判定两条直线的位置关系.
例2
感悟新知
方法点拨
判定两条直线平行的方法:
●若涉及相交问题,则用平行线的定义;
●若涉及三条直线的位置关系问题, 则用平行公理的推论,较常用的方法是平行公理的推论 .
感悟新知
解:(1)因为a ∥ b,b ∥ c,所以a ∥ c.
理由:如果两条直线都和第三条直线平行,那么这两条直线平行.
(2)因为直线a,d 都过点M,且a ∥ c,所以d 与c 相交.
理由:经过直线外一点,有且只有一条直线与这条直线平行.
感悟新知
知识点
同位角、内错角、同旁内角
3
1. “三线八角” 两条直线被第三条直线所截形成八个角,习惯上称为“三线八角”,它们构成了同位角、内错角、同旁内角 . 如图10.2-4 所示,两条直线 a 和 b 被第三条直线 l所截 .
感悟新知
2. 同位角、内错角、同旁内角的定义
(1) ∠ 1 与∠ 5 在截线 l 的同旁,又都在被截直线 a 和 b 相同的一侧,具有这样位置关系的一对角叫同位角 . 再如∠ 2 与∠ 6,∠ 3 与∠ 7,∠ 4 与∠ 8.
(2) ∠ 5 与∠ 3 在截线 l 的两旁,且在被截直线 a, b 之间,具有这样位置关系的一对角叫内错角 . 再如∠ 4 与∠ 6.
(3) ∠ 5 与∠ 4 在截线 l 的同旁,且在被截直线 a, b 之间,具有这样位置关系的一对角叫同旁内角 . 再如∠ 3与∠ 6.
感悟新知
特别解读
识别同位角、内错角、 同旁内角, 第一步是要分清截线和被截线(两个角的公共边所在的直线为截线,另两条线为被截线) ;
第二步是根据两角在截线和被截线的具体位置,结合各类位置角的定义确定它们的具体关系 . 在截线同旁(同侧 )找同位角(两个角都在被截线的上方或
感悟新知
下方,形似字母“F”)、同旁内角(两个角在被截线之间(内),形似字母“U”).
在截线不同旁 (两侧) 找内错角、即两条被截线之间、截线两侧(错开),形似字母“Z”.
感悟新知
如图 10.2-5,结合图形解答下列问题:
(1) ∠ 1 与∠ 2 是直线______ 和直线_____ 被第三条直线____所截而成的 ____角;
(2) ∠ 2 与∠ 3 是直线 _______和直线_______ 被第三条直线____所截而成的_____ 角;
(3) ∠ 4 与∠ A 是直线_______
和直线______ 被第三条直线___所截而成的 _____角 .
例 3
感悟新知
解题秘方:根据同位角、内错角和同旁内角的定义确定答案 .
解: (1) ∠ 1 与∠ 2 都有一条边在直线 BC 上,另一条边分别在直线 CE, AB 上,两角都在直线 BC 的上方,分别在直线 CE,AB 的右侧,所以∠ 1 与∠ 2 是直线 CE 和直线 AB 被直线 BC 所截而成的同位角;
感悟新知
(2) ∠ 2 与∠ 3 都有一条边在直线 BC 上,另一条边
分别在直线 AB, AC 上,两角都在直线 BC 的上方,在直线AB, AC 之间,所以∠ 2 与∠ 3 是直线 AB 和直线 AC 被直线BC 所截而成的同旁内角;
(3) ∠ 4 与∠ A 都有一条边在直线 AC 上,另一条边分别在直线 CE, AB 上,两角分别在直线 AC 的两侧,在直线CE, AB 之间,所以∠ 4 与∠ A 是直线 CE 和直线 AB 被直线AC 所截而成的内错角 .
感悟新知
答案: (1) CE; AB; BC;同位
(2) AB; AC; BC;同旁内
(3) CE; AB; AC;内错
感悟新知
方法点拨
识别同位角、内错角和同旁内角的方法:
1. 定义法:一看三线、二找截线、三查位置来分辨,这三种角的共同特征是:一对边共线,不共顶点,另一对边分别在两条直线上,再根据位置关系确定是哪种角;
2. 分离图形法:通过分离图形,把每一对角从复杂图形中分离出来,观察分离出的角的形状结构特征,按定义法加以区分;
感悟新知
3. 特征法:把相关的一对角用彩笔描出,看其是否符合“F”“Z”“U” 形特征;
4. 方位法:同位角:同左、同上;同左、同下;同右、同上;同右、同下;内错角:同内、异侧;同旁内角:同内、同侧 .
知识点
平行线的判定判定的基本事实
感悟新知
4
1. 基本事实 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
感悟新知
特别解读:(1)构成同位角的两条被截线不一定平行,只有形成的一对同位角相等,这两条被截线才平行.
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁.
感悟新知
2. 表达方式:如图10.2-6,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(同位角相等,两直线平行).
感悟新知
特别解读
判定两直线平行的方法
●直线的位置关系:
(1) 同一平面内不相交的两条直线平行.
(2) 同平行于第三条直线的两条直线平行.
●角的大小关系:
同位角相等,两直线平行.
感悟新知
如图10.2-7, 已知直线AB,CD 被直线EF 所截,∠ 1+ ∠ 2=180°,AB 与CD 平行吗?请说明理由.
例 4
感悟新知
解法提醒
判断两条直线是否平行,当题中涉及角的关系时,则可通过找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行,否则不平行 .
解题秘方:找出一对同位角,通过已知条件说明这对同位角相等来说明两条直线平行.
感悟新知
解:AB ∥ CD.
理由如下:
因为∠ 1+ ∠ 2=180°,
∠ 2+ ∠ 3=180°,
所以∠ 1= ∠ 3(同角的补角相等).
所以AB ∥ CD(同位角相等,两直线平行).
知识点
平行线的判定方法2
感悟新知
5
1. 方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
感悟新知
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的.
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
感悟新知
2. 表达方式:如图10.2-8,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
感悟新知
特别提醒
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等,这两条被截线才平行.
感悟新知
如图10.2-9,已知∠ ADE=60 °,DF 平分∠ ADE,
∠ 1=30°,试说明DF ∥ BE.
例5
解题秘方:先找出DF 和BE 被DE这两条被截线形成的一对内错角,然后利用条件说明这对内错角相等来说明这两条被截线平行.
感悟新知
解法提醒
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系 .
感悟新知
解:因为DF 平分∠ ADE(已知),
所以∠ EDF= ∠ ADE(角平分线的定义).
又因为∠ ADE=60° (已知) ,所以∠ EDF=30°.
又因为∠ 1=30° (已知) ,所以∠ EDF= ∠ 1.
所以DF ∥ BE (内错角相等,两直线平行).
知识点
平行线的判定方法3
感悟新知
6
1. 方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
感悟新知
特别解读:利用同旁内角说明两直线平行时,同旁内角之间的关系是互补,不是相等 .
感悟新知
2. 表达方式:如图10.2-10,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
感悟新知
如图10.2-11, 直线AE,CD 相交于点O, 如果
∠ A=110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
例 6
解题秘方:找出AB,CD 被AE 所截形成的同旁内角,利用两个角之间的数量关系来说明这两条直线平行.
感悟新知
解法提醒
●本题运用了数形结合思想 . 平行线的判定是由角之间的数量关系到直线的位置关系的判定 .
●说明两直线平行时,一般都要结合对顶角、补角等知识来说明.
感悟新知
解:因为∠ 1= ∠ AOD(对顶角相等),∠ 1=70°,
所以∠ AOD=70°.
又因为∠ A=110°,
所以∠ A+ ∠ AOD=180°.
所以AB ∥ CD(同旁内角互补,两直线平行).
知识点
平行线判定方法的推论
感悟新知
7
1. 判定方法 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.
简称:在同一平面内,垂直于同
一条直线的两条直线平行.
表达方式:如图10.2-12,直线a,b,c 在同一平面内.
因为a ⊥ b,a ⊥ c,所以b ∥ c.
感悟新知
2. 拓展
a,b,c 为同一平面内的三条不重合直线,在下列结论中:① a ⊥ b;② a ⊥ c;③ b ∥ c. 已知其中任意两个结论,总能推出第三个结论成立,即如果 a ⊥ b, a ⊥ c,那么 b ∥ c;如果 a ⊥ b, b ∥ c,那么a ⊥ c;如果 a ⊥ c, b ∥ c,那么 a ⊥ b.
感悟新知
特别解读
1.三条直线“在同一平面内”是前提,丢掉这个前提,结论不一定成立.
2.本结论(方法) 可看成是判定方法1,2,3 的推论,因为它可由判定方法1,2,3得到.
感悟新知
如图10.2-13,AB ⊥ EF 于B,CD ⊥ EF 于D,
∠ 1= ∠ 2.
(1)请说明AB ∥ CD 的理由;
(2)试问BM 与DN 是否平行?为什么?
解题秘方:根据平行的几种判定方法的模型,从图中找出符合判定的条件,选用合适的方法进行说明.
例7
感悟新知
解法提醒
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线 .
方法二:如果两条直线都和第三条直线平行,那么这两条直线平行 .
方法三:同位角相等,两直线平行 .
感悟新知
方法四:内错角相等,两直线平行 .
方法五:同旁内角互补,两直线平行 .
方法六:在同一平面内,垂直于同一条直线的两条直线平行 .
感悟新知
解:(1)因为AB ⊥ EF,CD ⊥ EF,
所以AB ∥ CD(在同一平面内,垂直于同一条直线的两条直线平行).
感悟新知
(2)BM ∥ DN.
理由如下:因为AB ⊥ EF,CD ⊥ EF,
所以∠ ABE= ∠ CDE=90°.
又因为∠ 1= ∠ 2,
所以∠ ABE-∠ 1= ∠ CDE-∠ 2(等式的性质),
即∠ MBE= ∠ NDE.
所以BM ∥ DN(同位角相等,两直线平行).
感悟新知
警示误区:∠ 1 和∠ 2 不是同位角,不能误认为∠ 1 和∠ 2 是同位角,直接得出 BM ∥ DN,要得到 BM ∥ DN,应说明∠ MBE= ∠ NDE.
课堂小结
平行线的判定
平行线
内错角相等
同位角相等
同旁内角互补
定义
画法
位置
关系
判定
三线八角
基本事实
10.2 平行线的判定
第十章 相交线、平行线与平移
学习目标
课时讲解
1
平行线的定义及画法
基本事实及其推论
同位角、内错角、同旁内角
平行线的判定的基本事实
平行线的判定方法 2
平行线的判定方法 3
平行线判定方法的推论
逐点
导讲练
课堂小结
作业提升
学习目标
课时流程
2
知识点
平行线的定义及画法
感悟新知
1
1. 定义 在同一平面内不相交的两条直线叫做平行线.
特别提醒:平行线的定义三要素:
(1)在同一平面内;
(2)不相交;
(3)都是直线.
感悟新知
2. 表示方法:用“∥”表示平行,如图10.2-1,记作“AB ∥ CD”或“CD ∥ AB ” ,读作“AB 平行于CD ”或“CD 平行于AB ”.
感悟新知
特别解读
1. 在同一平面内,不重合的两条直线的位置关系: ●相交; ●平行.
2. 经过直线上一点不可以作已知直线的平行线 .
3. 画线段或射线的平行线是画它们所在直线的平行线 .
感悟新知
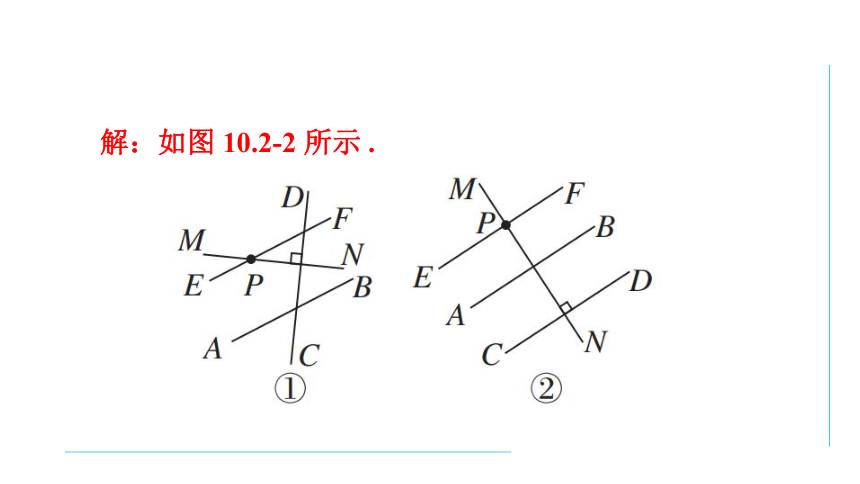
读下列语句,并画出图形 . 直线 AB, CD 是两条直
线, P 是直线 AB, CD 外的一点,直线 EF 经过点 P 与 AB 平行,直线 MN 经过点 P 与 CD 垂直 .
例 1
感悟新知
解题秘方:按照语句的要求,结合平行线的画法进行作图 .
解法提醒
根据语句画图时,要注意画出的图形符合语句的要求,若语句中没有说清楚的,要考虑各种情况,如本题中AB,CD 之间没有指明位置关系,所以画图时可以平行也可以相交 .
感悟新知
解:如图 10.2-2 所示 .
知识点
基本事实及其推论
感悟新知
2
1. 基本事实 经过直线外一点,有且只有一条直线平行于这条直线.
特别提醒:基本事实的前提是经过直线外一点,若点在直线上,则不可能有平行线.
特别解读
“有且只有”强调这样的直线的存在性和唯一性.
感悟新知
2. 推论 如果两条直线都和第三条直线平行,那么这两条直线平行.
简称:平行于第三条直线的两条直线平行.
表达方式:如果a ∥ c,b ∥ c,那么a ∥ b.
感悟新知
如图10.2-3,直线a ∥ b,b ∥ c,d 与a 相交于点M.
(1)试判断直线a,c 的位置关系,并说明理由;
(2)判断c 与d 的位置关系,并说明理由.
解题秘方:根据平行公理及其推论判定两条直线的位置关系.
例2
感悟新知
方法点拨
判定两条直线平行的方法:
●若涉及相交问题,则用平行线的定义;
●若涉及三条直线的位置关系问题, 则用平行公理的推论,较常用的方法是平行公理的推论 .
感悟新知
解:(1)因为a ∥ b,b ∥ c,所以a ∥ c.
理由:如果两条直线都和第三条直线平行,那么这两条直线平行.
(2)因为直线a,d 都过点M,且a ∥ c,所以d 与c 相交.
理由:经过直线外一点,有且只有一条直线与这条直线平行.
感悟新知
知识点
同位角、内错角、同旁内角
3
1. “三线八角” 两条直线被第三条直线所截形成八个角,习惯上称为“三线八角”,它们构成了同位角、内错角、同旁内角 . 如图10.2-4 所示,两条直线 a 和 b 被第三条直线 l所截 .
感悟新知
2. 同位角、内错角、同旁内角的定义
(1) ∠ 1 与∠ 5 在截线 l 的同旁,又都在被截直线 a 和 b 相同的一侧,具有这样位置关系的一对角叫同位角 . 再如∠ 2 与∠ 6,∠ 3 与∠ 7,∠ 4 与∠ 8.
(2) ∠ 5 与∠ 3 在截线 l 的两旁,且在被截直线 a, b 之间,具有这样位置关系的一对角叫内错角 . 再如∠ 4 与∠ 6.
(3) ∠ 5 与∠ 4 在截线 l 的同旁,且在被截直线 a, b 之间,具有这样位置关系的一对角叫同旁内角 . 再如∠ 3与∠ 6.
感悟新知
特别解读
识别同位角、内错角、 同旁内角, 第一步是要分清截线和被截线(两个角的公共边所在的直线为截线,另两条线为被截线) ;
第二步是根据两角在截线和被截线的具体位置,结合各类位置角的定义确定它们的具体关系 . 在截线同旁(同侧 )找同位角(两个角都在被截线的上方或
感悟新知
下方,形似字母“F”)、同旁内角(两个角在被截线之间(内),形似字母“U”).
在截线不同旁 (两侧) 找内错角、即两条被截线之间、截线两侧(错开),形似字母“Z”.
感悟新知
如图 10.2-5,结合图形解答下列问题:
(1) ∠ 1 与∠ 2 是直线______ 和直线_____ 被第三条直线____所截而成的 ____角;
(2) ∠ 2 与∠ 3 是直线 _______和直线_______ 被第三条直线____所截而成的_____ 角;
(3) ∠ 4 与∠ A 是直线_______
和直线______ 被第三条直线___所截而成的 _____角 .
例 3
感悟新知
解题秘方:根据同位角、内错角和同旁内角的定义确定答案 .
解: (1) ∠ 1 与∠ 2 都有一条边在直线 BC 上,另一条边分别在直线 CE, AB 上,两角都在直线 BC 的上方,分别在直线 CE,AB 的右侧,所以∠ 1 与∠ 2 是直线 CE 和直线 AB 被直线 BC 所截而成的同位角;
感悟新知
(2) ∠ 2 与∠ 3 都有一条边在直线 BC 上,另一条边
分别在直线 AB, AC 上,两角都在直线 BC 的上方,在直线AB, AC 之间,所以∠ 2 与∠ 3 是直线 AB 和直线 AC 被直线BC 所截而成的同旁内角;
(3) ∠ 4 与∠ A 都有一条边在直线 AC 上,另一条边分别在直线 CE, AB 上,两角分别在直线 AC 的两侧,在直线CE, AB 之间,所以∠ 4 与∠ A 是直线 CE 和直线 AB 被直线AC 所截而成的内错角 .
感悟新知
答案: (1) CE; AB; BC;同位
(2) AB; AC; BC;同旁内
(3) CE; AB; AC;内错
感悟新知
方法点拨
识别同位角、内错角和同旁内角的方法:
1. 定义法:一看三线、二找截线、三查位置来分辨,这三种角的共同特征是:一对边共线,不共顶点,另一对边分别在两条直线上,再根据位置关系确定是哪种角;
2. 分离图形法:通过分离图形,把每一对角从复杂图形中分离出来,观察分离出的角的形状结构特征,按定义法加以区分;
感悟新知
3. 特征法:把相关的一对角用彩笔描出,看其是否符合“F”“Z”“U” 形特征;
4. 方位法:同位角:同左、同上;同左、同下;同右、同上;同右、同下;内错角:同内、异侧;同旁内角:同内、同侧 .
知识点
平行线的判定判定的基本事实
感悟新知
4
1. 基本事实 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
感悟新知
特别解读:(1)构成同位角的两条被截线不一定平行,只有形成的一对同位角相等,这两条被截线才平行.
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁.
感悟新知
2. 表达方式:如图10.2-6,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(同位角相等,两直线平行).
感悟新知
特别解读
判定两直线平行的方法
●直线的位置关系:
(1) 同一平面内不相交的两条直线平行.
(2) 同平行于第三条直线的两条直线平行.
●角的大小关系:
同位角相等,两直线平行.
感悟新知
如图10.2-7, 已知直线AB,CD 被直线EF 所截,∠ 1+ ∠ 2=180°,AB 与CD 平行吗?请说明理由.
例 4
感悟新知
解法提醒
判断两条直线是否平行,当题中涉及角的关系时,则可通过找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行,否则不平行 .
解题秘方:找出一对同位角,通过已知条件说明这对同位角相等来说明两条直线平行.
感悟新知
解:AB ∥ CD.
理由如下:
因为∠ 1+ ∠ 2=180°,
∠ 2+ ∠ 3=180°,
所以∠ 1= ∠ 3(同角的补角相等).
所以AB ∥ CD(同位角相等,两直线平行).
知识点
平行线的判定方法2
感悟新知
5
1. 方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
感悟新知
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的.
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
感悟新知
2. 表达方式:如图10.2-8,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
感悟新知
特别提醒
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等,这两条被截线才平行.
感悟新知
如图10.2-9,已知∠ ADE=60 °,DF 平分∠ ADE,
∠ 1=30°,试说明DF ∥ BE.
例5
解题秘方:先找出DF 和BE 被DE这两条被截线形成的一对内错角,然后利用条件说明这对内错角相等来说明这两条被截线平行.
感悟新知
解法提醒
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系 .
感悟新知
解:因为DF 平分∠ ADE(已知),
所以∠ EDF= ∠ ADE(角平分线的定义).
又因为∠ ADE=60° (已知) ,所以∠ EDF=30°.
又因为∠ 1=30° (已知) ,所以∠ EDF= ∠ 1.
所以DF ∥ BE (内错角相等,两直线平行).
知识点
平行线的判定方法3
感悟新知
6
1. 方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
感悟新知
特别解读:利用同旁内角说明两直线平行时,同旁内角之间的关系是互补,不是相等 .
感悟新知
2. 表达方式:如图10.2-10,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
感悟新知
如图10.2-11, 直线AE,CD 相交于点O, 如果
∠ A=110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
例 6
解题秘方:找出AB,CD 被AE 所截形成的同旁内角,利用两个角之间的数量关系来说明这两条直线平行.
感悟新知
解法提醒
●本题运用了数形结合思想 . 平行线的判定是由角之间的数量关系到直线的位置关系的判定 .
●说明两直线平行时,一般都要结合对顶角、补角等知识来说明.
感悟新知
解:因为∠ 1= ∠ AOD(对顶角相等),∠ 1=70°,
所以∠ AOD=70°.
又因为∠ A=110°,
所以∠ A+ ∠ AOD=180°.
所以AB ∥ CD(同旁内角互补,两直线平行).
知识点
平行线判定方法的推论
感悟新知
7
1. 判定方法 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.
简称:在同一平面内,垂直于同
一条直线的两条直线平行.
表达方式:如图10.2-12,直线a,b,c 在同一平面内.
因为a ⊥ b,a ⊥ c,所以b ∥ c.
感悟新知
2. 拓展
a,b,c 为同一平面内的三条不重合直线,在下列结论中:① a ⊥ b;② a ⊥ c;③ b ∥ c. 已知其中任意两个结论,总能推出第三个结论成立,即如果 a ⊥ b, a ⊥ c,那么 b ∥ c;如果 a ⊥ b, b ∥ c,那么a ⊥ c;如果 a ⊥ c, b ∥ c,那么 a ⊥ b.
感悟新知
特别解读
1.三条直线“在同一平面内”是前提,丢掉这个前提,结论不一定成立.
2.本结论(方法) 可看成是判定方法1,2,3 的推论,因为它可由判定方法1,2,3得到.
感悟新知
如图10.2-13,AB ⊥ EF 于B,CD ⊥ EF 于D,
∠ 1= ∠ 2.
(1)请说明AB ∥ CD 的理由;
(2)试问BM 与DN 是否平行?为什么?
解题秘方:根据平行的几种判定方法的模型,从图中找出符合判定的条件,选用合适的方法进行说明.
例7
感悟新知
解法提醒
判定两直线平行的方法:
方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线 .
方法二:如果两条直线都和第三条直线平行,那么这两条直线平行 .
方法三:同位角相等,两直线平行 .
感悟新知
方法四:内错角相等,两直线平行 .
方法五:同旁内角互补,两直线平行 .
方法六:在同一平面内,垂直于同一条直线的两条直线平行 .
感悟新知
解:(1)因为AB ⊥ EF,CD ⊥ EF,
所以AB ∥ CD(在同一平面内,垂直于同一条直线的两条直线平行).
感悟新知
(2)BM ∥ DN.
理由如下:因为AB ⊥ EF,CD ⊥ EF,
所以∠ ABE= ∠ CDE=90°.
又因为∠ 1= ∠ 2,
所以∠ ABE-∠ 1= ∠ CDE-∠ 2(等式的性质),
即∠ MBE= ∠ NDE.
所以BM ∥ DN(同位角相等,两直线平行).
感悟新知
警示误区:∠ 1 和∠ 2 不是同位角,不能误认为∠ 1 和∠ 2 是同位角,直接得出 BM ∥ DN,要得到 BM ∥ DN,应说明∠ MBE= ∠ NDE.
课堂小结
平行线的判定
平行线
内错角相等
同位角相等
同旁内角互补
定义
画法
位置
关系
判定
三线八角
基本事实
