北师大版八年级下册6.1.1 平行四边形的边和角的性质 练习题 (含答案)
文档属性
| 名称 | 北师大版八年级下册6.1.1 平行四边形的边和角的性质 练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 328.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 19:37:05 | ||
图片预览


文档简介
6.1.1 平行四边形的边和角的性质
一、单项选择题
1.如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A.2 B.4 C.6 D.8
2.如图,在 ABCD中,∠BCD的平分线交BA的延长线于点E,若AE=3,AD=8,则 ABCD的周长为( )
A.22 B.24 C.26 D.28
3.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,BC=8,则EF等于( )
A.2 B.4 C.6 D.8
4.如图,在 ABCD中,∠ABC和∠BCD的平分线交于边AD上的一点E,且BE=4,CE=3,则AB等于( )
A.2.5 B.3 C.3.5 D.4.5
5. 如图,在 ABCD中,E是AB延长线上的一点,若∠D=120°,则∠1的度数为( )
A.40° B.50° C.60° D.70°
二、填空题
6.如图,在 ABCD中,AE⊥CD于点E,若∠B=65°,则∠DAE=________.
7.如图,在平面直角坐标系中, ABCD的顶点A,B,D的坐标分别是(-2,0),(3,0),(0,3),则顶点C的坐标是____________.
8. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处.若∠1=56°,∠2=42°,则∠A的度数为____________.
9. 如图,点E在 ABCD的对角线上,AE=BE=BC,∠D=105°,则∠BAC的度数是____________.
10. 如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为 ______.
11. 如图,将三角尺ABC分别沿射线AC,AB平移到A1B1C1,A2B2C2的位置,延长A1B1,A2C2交于点A3,则:
∵∠BAC=___________,∠BAC=____________,∴AA2∥__________,AA1∥____________,
∴四边形AA1A3A2是______________形.
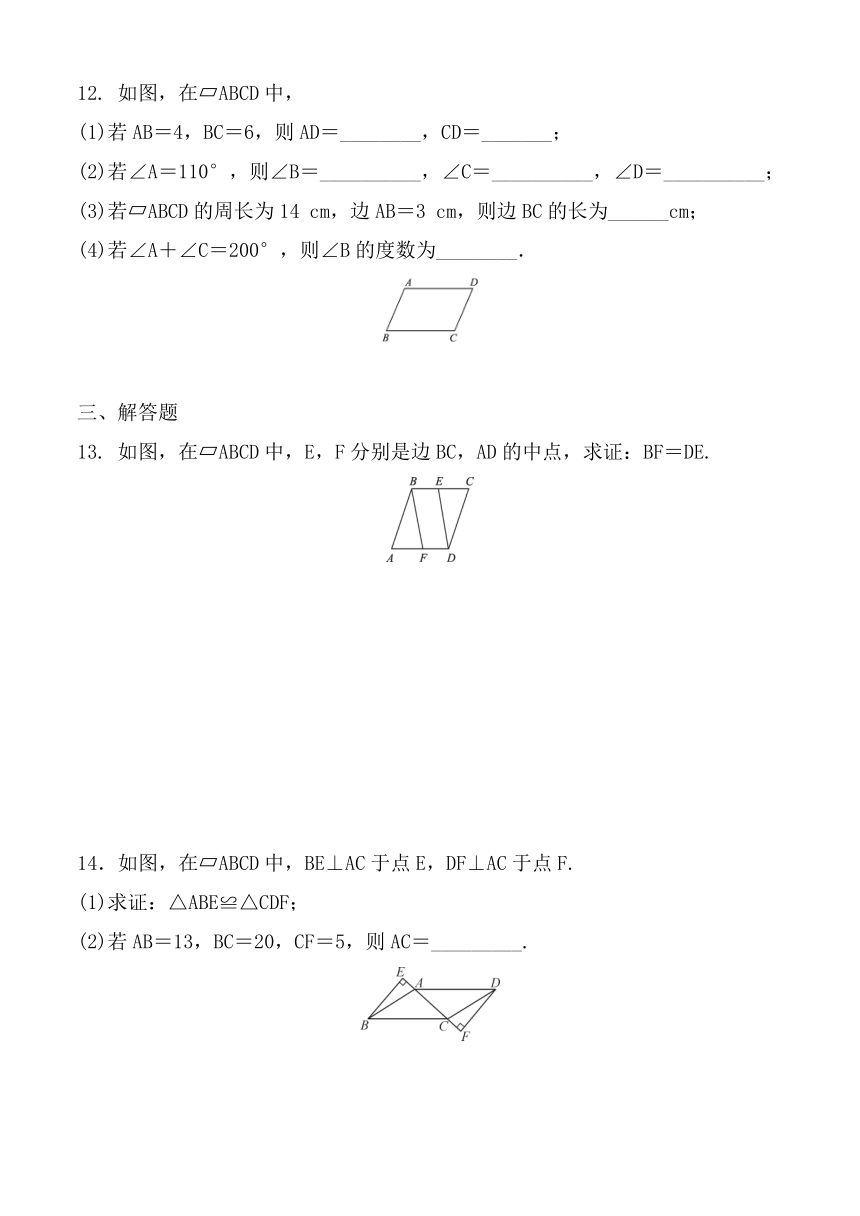
12. 如图,在 ABCD中,
(1)若AB=4,BC=6,则AD=________,CD=_______;
(2)若∠A=110°,则∠B=__________,∠C=__________,∠D=__________;
(3)若 ABCD的周长为14 cm,边AB=3 cm,则边BC的长为______cm;
(4)若∠A+∠C=200°,则∠B的度数为________.
三、解答题
13. 如图,在 ABCD中,E,F分别是边BC,AD的中点,求证:BF=DE.
14.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=13,BC=20,CF=5,则AC=_________.
15.如图,在 ABCD中,BE,DG分别平分∠ABC,∠ADC,交AC于点E,G.
(1)求证:BE∥DG,BE=DG;
(2)过点E作EF⊥AB,垂足为F,若 ABCD的周长为56,EF=6,求△ABC的面积.
16.如图,在 ABCD中,分别以边BC,CD为边作等腰△BCF,等腰△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)若AF⊥AE,求证:BF⊥BC.
答案:
一、
1-5 BCBAC
二、
6. 25°
7. (5,3)
8. 110°
9. 25°
10. 8
11. ∠B1A1C1 ∠B2A2C2 A1A3 A2A3 平行四边
12. (1) 6 4
(2) 70° 110° 70°
(3) 4 80°
三、
13. 证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C.又∵E,F分别是边BC,AD的中点,∴AF=AD=BC=CE,∴△ABF≌△CDE(SAS),∴BF=DE
14. 解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAC=∠DCA,∴∠EAB=∠FCD.又∵BE⊥AC,DF⊥AC,∴∠BEA=∠DFC=90°,∴△ABE≌△CDF
(2)∵△ABE≌△CDF,∴AE=CF=5,∴BE===12,∴CE===16,∴AC=CE-AE=16-5=11
15. 解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∠ADC=∠ABC,∴∠DAC=∠BCA.又∵BE,DG分别平分∠ABC,∠ADC,∴∠ADG=∠ADC=∠ABC=∠CBE,∴△ADG≌△CBE(ASA),∴BE=DG,∠AGD=∠CEB,∴∠DGC=∠BEA,∴DG∥BE
(2)过点E作EH⊥BC于点H,∵BE平分∠ABC,EF⊥AB,EH⊥BC,∴EH=EF=6.又∵C ABCD=AB+BC+CD+AD=AB+BC+AB+BC=2(AB+BC)=56,∴AB+BC=28,∴S△ABC=S△ABE+S△BCE=AB·EF+BC·EH=EF·(AB+BC)=×6×28=84
16. 证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠ABC=∠ADC.又∵BC=BF,CD=DE,∴BF=AD,AB=DE.又∵∠ADE+∠ADC+∠EDC=360°,∠ABF+∠ABC+∠CBF=360°,∠EDC=∠CBF,∴∠ADE=∠ABF,∴△ABF≌△EDA
(2)延长FB交AD于点H,∵AE⊥AF,∴∠EAF=90°.∵△ABF≌△EDA,∴∠EAD=∠AFB.又∵∠EAD+∠FAH=90°,∴∠FAH+∠AFB=90°,∴∠AHF=90°,即FB⊥AD.又∵AD∥BC,∴BF⊥BC
一、单项选择题
1.如图,在 ABCD中,已知AB=12,AD=8,∠ABC的平分线BM交CD边于点M,则DM的长为( )
A.2 B.4 C.6 D.8
2.如图,在 ABCD中,∠BCD的平分线交BA的延长线于点E,若AE=3,AD=8,则 ABCD的周长为( )
A.22 B.24 C.26 D.28
3.如图,在 ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,BC=8,则EF等于( )
A.2 B.4 C.6 D.8
4.如图,在 ABCD中,∠ABC和∠BCD的平分线交于边AD上的一点E,且BE=4,CE=3,则AB等于( )
A.2.5 B.3 C.3.5 D.4.5
5. 如图,在 ABCD中,E是AB延长线上的一点,若∠D=120°,则∠1的度数为( )
A.40° B.50° C.60° D.70°
二、填空题
6.如图,在 ABCD中,AE⊥CD于点E,若∠B=65°,则∠DAE=________.
7.如图,在平面直角坐标系中, ABCD的顶点A,B,D的坐标分别是(-2,0),(3,0),(0,3),则顶点C的坐标是____________.
8. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处.若∠1=56°,∠2=42°,则∠A的度数为____________.
9. 如图,点E在 ABCD的对角线上,AE=BE=BC,∠D=105°,则∠BAC的度数是____________.
10. 如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为 ______.
11. 如图,将三角尺ABC分别沿射线AC,AB平移到A1B1C1,A2B2C2的位置,延长A1B1,A2C2交于点A3,则:
∵∠BAC=___________,∠BAC=____________,∴AA2∥__________,AA1∥____________,
∴四边形AA1A3A2是______________形.
12. 如图,在 ABCD中,
(1)若AB=4,BC=6,则AD=________,CD=_______;
(2)若∠A=110°,则∠B=__________,∠C=__________,∠D=__________;
(3)若 ABCD的周长为14 cm,边AB=3 cm,则边BC的长为______cm;
(4)若∠A+∠C=200°,则∠B的度数为________.
三、解答题
13. 如图,在 ABCD中,E,F分别是边BC,AD的中点,求证:BF=DE.
14.如图,在 ABCD中,BE⊥AC于点E,DF⊥AC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=13,BC=20,CF=5,则AC=_________.
15.如图,在 ABCD中,BE,DG分别平分∠ABC,∠ADC,交AC于点E,G.
(1)求证:BE∥DG,BE=DG;
(2)过点E作EF⊥AB,垂足为F,若 ABCD的周长为56,EF=6,求△ABC的面积.
16.如图,在 ABCD中,分别以边BC,CD为边作等腰△BCF,等腰△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)若AF⊥AE,求证:BF⊥BC.
答案:
一、
1-5 BCBAC
二、
6. 25°
7. (5,3)
8. 110°
9. 25°
10. 8
11. ∠B1A1C1 ∠B2A2C2 A1A3 A2A3 平行四边
12. (1) 6 4
(2) 70° 110° 70°
(3) 4 80°
三、
13. 证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C.又∵E,F分别是边BC,AD的中点,∴AF=AD=BC=CE,∴△ABF≌△CDE(SAS),∴BF=DE
14. 解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴∠BAC=∠DCA,∴∠EAB=∠FCD.又∵BE⊥AC,DF⊥AC,∴∠BEA=∠DFC=90°,∴△ABE≌△CDF
(2)∵△ABE≌△CDF,∴AE=CF=5,∴BE===12,∴CE===16,∴AC=CE-AE=16-5=11
15. 解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∠ADC=∠ABC,∴∠DAC=∠BCA.又∵BE,DG分别平分∠ABC,∠ADC,∴∠ADG=∠ADC=∠ABC=∠CBE,∴△ADG≌△CBE(ASA),∴BE=DG,∠AGD=∠CEB,∴∠DGC=∠BEA,∴DG∥BE
(2)过点E作EH⊥BC于点H,∵BE平分∠ABC,EF⊥AB,EH⊥BC,∴EH=EF=6.又∵C ABCD=AB+BC+CD+AD=AB+BC+AB+BC=2(AB+BC)=56,∴AB+BC=28,∴S△ABC=S△ABE+S△BCE=AB·EF+BC·EH=EF·(AB+BC)=×6×28=84
16. 证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠ABC=∠ADC.又∵BC=BF,CD=DE,∴BF=AD,AB=DE.又∵∠ADE+∠ADC+∠EDC=360°,∠ABF+∠ABC+∠CBF=360°,∠EDC=∠CBF,∴∠ADE=∠ABF,∴△ABF≌△EDA
(2)延长FB交AD于点H,∵AE⊥AF,∴∠EAF=90°.∵△ABF≌△EDA,∴∠EAD=∠AFB.又∵∠EAD+∠FAH=90°,∴∠FAH+∠AFB=90°,∴∠AHF=90°,即FB⊥AD.又∵AD∥BC,∴BF⊥BC
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
