广东省佛山市南海区2022-2023学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 广东省佛山市南海区2022-2023学年高二下学期期中考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 842.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 13:24:19 | ||
图片预览




文档简介
佛山市南海区2022-2023学年高二下学期期中考试
数学
(全卷共4页,时间:120分钟)
第Ⅰ卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.有4名同学参加跑步、跳远、跳高三个项目,每人限报1项,共有( )种报名方法.
A.64种 B.81种 C.32种 D.12种
2.已知实数列-1、x、y、z、-2成等比数列,则( )
A. B. C. D.
3.在数列中,,,则( )
A. B. C. D.
4.在“全面脱贫”行动中,贫困户小王2023年1月初向银行借了扶贫免息贷款10000元,用于自己开发的农产品、土特产品加工厂的原材料进货,因产品质优价廉,上市后供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底街缴房租800元和水电费400元,余款作为资金全部用于再进货,如此继续,预计2023年小王的农产品加工厂的年利润为( )(取,)
A.25000元 B.26000元 C.32000元 D.36000元
5.已知函数在处有极大值、则的值为( )
A.6 B.6或2 C.2 D.4或2
6.记数列的前项和为,满足,且,则的最小值为( )
A. B. C. D.
7.已知数列的前项和为,且,,则( )
A.55 B.50 C.110 D.210
8.设,,,则( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分.有选错的得0分.
9.某居委会举办的文苕汇演共6个节目,其中歌唱类节目3个,舞蹈类节目2个,语言类节目1个,则下列说法正确的是( )
A.若以歌唱类节目开场,则有360种不同的出场顺序
B.若舞蹈类节目相邻,则有120种出场顺序
C.若舞蹈类节目不相邻,则有40种不同的出场顺序
D.从中挑选2个不同类型的节目参加市艺术节,则有11种不同的选法
10.已知函数,则以下结论正确的是( )
A.函数存在极大值和极小值
B.
C.函数只有1个零点
D.对于任意实数,方程最多有4个实数解
11.在的展开式中,第3项的系数与倒数第3项的系数之比为,下列说法正确的有( ).
A. B.有理项有3项
C.系数最大项为第6项 D.第3项是二项式系数最大的项
12.定义:设是的导函数,是函数的导数。若方程有实数解,则称点为函数的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图像的对称中心,已知函数的对称中心为,则下列说法中正确的有( )A. ,
B.函数有三个零点
C.过可以作两条直线与图像相切
D.若函数在区间上有最大值,则
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,满分20分.
13.已知,则__________.
14.南海中学环保小组共有6名成员,该环保小组计划前往佛山市4个不圆的景区开展环保活动,要求每个景区至少有1人,且每个人只能去一个景区,则不同的分配方案有__________.
15.若直线与曲线相切,则_________.
l6.高斯是德国著名的数学家,近代数学的奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为“高斯函数”,例如:,.已知数列满足,,,若,为数列的前项和,则_________.
三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.
17.(10分)在各项均为正数的等差数列中,,,成等比数列.
(1)求数列的通项公式;
(2)设数列的前项和为,,证明:.
18.(12分)如图,圆台上底面半径为1,下底面半径为,AB为圆台下底面的一条直径,圆上点C满足,是圆台上底面的一条半径,点P,C在平面的同侧,且.
(1)证明:平面PAC;
(2)从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成的正弦值.
条件①:三棱锥的体积为;条件②:与圆台底面的夹角的正切值为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
19.(12分)已知数列的前项和为,且.
(1)求及数列的通项公式;
(2)在与之间插入个数,使得这个数依次组成公差为的等差数列,求数列的前项和.
20.(12分)已知函数,.
(1)讨论的单调性;
(2)若,求证:.
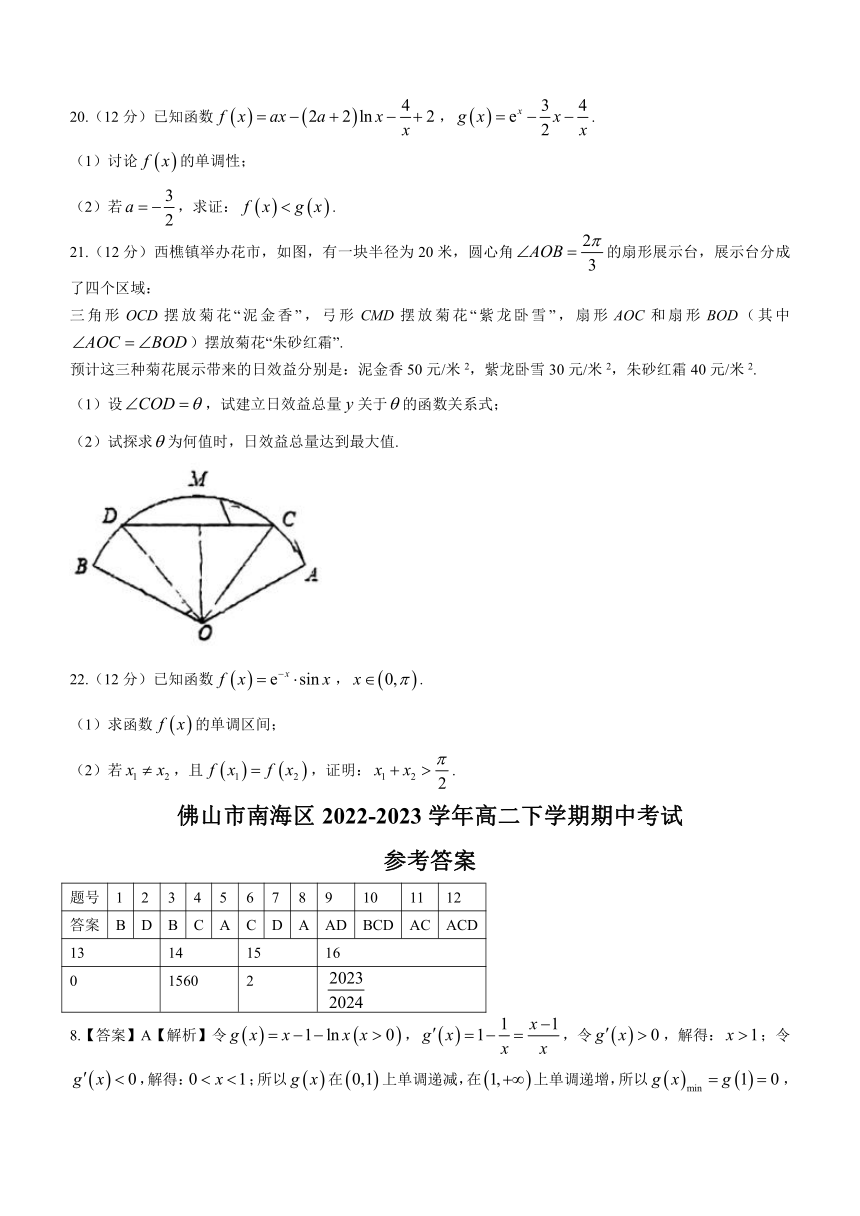
21.(12分)西樵镇举办花市,如图,有一块半径为20米,圆心角的扇形展示台,展示台分成了四个区域:
三角形OCD摆放菊花“泥金香”,弓形CMD摆放菊花“紫龙卧雪”,扇形AOC和扇形BOD(其中)摆放菊花“朱砂红霜”.
预计这三种菊花展示带来的日效益分别是:泥金香50元/米2,紫龙卧雪30元/米2,朱砂红霜40元/米2.
(1)设,试建立日效益总量关于的函数关系式;
(2)试探求为何值时,日效益总量达到最大值.
22.(12分)已知函数,.
(1)求函数的单调区间;
(2)若,且,证明:.
佛山市南海区2022-2023学年高二下学期期中考试
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B C A C D A AD BCD AC ACD
13 14 15 16
0 1560 2
8.【答案】A【解析】令,,令,解得:;令,解得:;所以在上单调递减,在上单调递增,所以,所以,由可知,设,则在区间上是减函数.且.所以函数在区间上是增函数.所以,即.即:.故选:A.
11.【答案】AC【解析】由题意知:,则第3项的系数为,倒数第3项的系数为,则有即,∴.A选项正确;
可得,当时所有的有理项为,,,,即,,,.B选项错误;
设展开式中第项的系数最大,则,∴,故系数最大项为,系数最大项为第6项.C选项正确;
,第4项和第5项是二项式系数最大的项,D错误.故选:AC.
15.【答案】2【解析】设切点为,,则,解得.
令,则,所以当时,,单调递减;
当时,,单调递增.所以,所以方程的根为.
16.【答案】【解析】由,得.又,所以数列构成以2为首项,2为公比的等比数列,所以.又,累加得,即,所以.又因为满足上式,所以.
所以.因为,所以,
即,所以.故.
所以.
17.【解析】(1)设等差数列的公差为,由已知得,
即,
又,
解得(舍负),则,所以.
(2)结合(1)得,
则,
所以
.
18.【解析】(1)取AC中点M,连接,,如图,
由题意,,
又,.又,,
故,,
所以四边形为平行四边形,
则,又面,平面,故平面
(2)选①:,又平面ABC,
所以三棱锥体积.所以.
选②:因为平面,所以为与底面所成的角,所以,又,所以;
以为坐标原点,,,所在直线为坐标轴建立如图空间直角坐标系.
则有,,,,,
故,,
设平面的法向量,故
令,解得,得,
设所求角的大小为,则.
所以直线与平面PBC所成角的正弦值为.
19.【解析】(1)由题意,当时,,解得,
当时,,即,解得,
当时,由,可得,两式相减,可得,
整理,得,∴数列是以2为首项,2为公比的等比数列,
∴,.
(2)由(1)可得,,,在与之间插入个数,使得这个数依次组成公差为的等差数列,则有,∴,∴,
∴,
,
两式相减得,
∴.
20.【解析】(1),
当时,,,所以在上递增,在上递减
当时,或,,
此时在,上递增,在上递减;
当时,,所以在上递增;
当时,或,,
此时在,上递增,在上递减;
(2)当,,要证,只需证,令
则,,故在上递减,
又,,故存在,使得,即,即
且,,故在上递增,在上递减,
所以,
又,所以,所以,所以,
所以,所以时,.
【备注】此题可以使用切线放缩,即证明不等式.
21.【解析】(1)依题意得,,
则
,
其中,.
(2),令,得,
当,,函数递增,当时,,函数递减.
所以,是函数的极大值点,且唯一;从而当时,日效益总量可取得最大值.
22.【解析】(1),,
由得,当时,;当时,
∴在上单调递增,在上单调递减.
(2)∵,且,
∴由(1)知,不妨设.
要证,只需证明,而,在上单调递减,
故只需证明;又,
∴只需证明.
令函数,
则
.
当时,,,故,
∴在上单调递增,
故在上,
∴成立,故成立.
【极值点偏移·知识链接】①函数满足定义域内任意自变量都有,则函数关于直线对称;可以理解为函数在对称轴两侧,函数值变化快慢相同,且若为单峰函数,则
必为的极值点.
如二次函数的顶点就是极值点,若的两根的中点为,则刚好有,即极值点在两根的正中间,也就是极值点没有偏移.
②若相等变为不等,则为极值点偏移:若单峰函数的极值点为,且函数满足定义域内左侧的任意都有或,则函数极值点左右侧变化快慢不同.
故单峰函数定义域内任意不同的实数,满足,则与极值点必有确定的大小关系:
若,则称为极值点左偏.
若,则称为极值点右偏.
如:的极值点刚好在方程的两根中点的左边,我们称之为极值点左偏.
数学
(全卷共4页,时间:120分钟)
第Ⅰ卷(选择题 共60分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.有4名同学参加跑步、跳远、跳高三个项目,每人限报1项,共有( )种报名方法.
A.64种 B.81种 C.32种 D.12种
2.已知实数列-1、x、y、z、-2成等比数列,则( )
A. B. C. D.
3.在数列中,,,则( )
A. B. C. D.
4.在“全面脱贫”行动中,贫困户小王2023年1月初向银行借了扶贫免息贷款10000元,用于自己开发的农产品、土特产品加工厂的原材料进货,因产品质优价廉,上市后供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底街缴房租800元和水电费400元,余款作为资金全部用于再进货,如此继续,预计2023年小王的农产品加工厂的年利润为( )(取,)
A.25000元 B.26000元 C.32000元 D.36000元
5.已知函数在处有极大值、则的值为( )
A.6 B.6或2 C.2 D.4或2
6.记数列的前项和为,满足,且,则的最小值为( )
A. B. C. D.
7.已知数列的前项和为,且,,则( )
A.55 B.50 C.110 D.210
8.设,,,则( )
A. B. C. D.
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,选对但不全的得2分.有选错的得0分.
9.某居委会举办的文苕汇演共6个节目,其中歌唱类节目3个,舞蹈类节目2个,语言类节目1个,则下列说法正确的是( )
A.若以歌唱类节目开场,则有360种不同的出场顺序
B.若舞蹈类节目相邻,则有120种出场顺序
C.若舞蹈类节目不相邻,则有40种不同的出场顺序
D.从中挑选2个不同类型的节目参加市艺术节,则有11种不同的选法
10.已知函数,则以下结论正确的是( )
A.函数存在极大值和极小值
B.
C.函数只有1个零点
D.对于任意实数,方程最多有4个实数解
11.在的展开式中,第3项的系数与倒数第3项的系数之比为,下列说法正确的有( ).
A. B.有理项有3项
C.系数最大项为第6项 D.第3项是二项式系数最大的项
12.定义:设是的导函数,是函数的导数。若方程有实数解,则称点为函数的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图像的对称中心,已知函数的对称中心为,则下列说法中正确的有( )A. ,
B.函数有三个零点
C.过可以作两条直线与图像相切
D.若函数在区间上有最大值,则
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,满分20分.
13.已知,则__________.
14.南海中学环保小组共有6名成员,该环保小组计划前往佛山市4个不圆的景区开展环保活动,要求每个景区至少有1人,且每个人只能去一个景区,则不同的分配方案有__________.
15.若直线与曲线相切,则_________.
l6.高斯是德国著名的数学家,近代数学的奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为“高斯函数”,例如:,.已知数列满足,,,若,为数列的前项和,则_________.
三、解答题:本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.
17.(10分)在各项均为正数的等差数列中,,,成等比数列.
(1)求数列的通项公式;
(2)设数列的前项和为,,证明:.
18.(12分)如图,圆台上底面半径为1,下底面半径为,AB为圆台下底面的一条直径,圆上点C满足,是圆台上底面的一条半径,点P,C在平面的同侧,且.
(1)证明:平面PAC;
(2)从条件①、条件②这两个条件中选择一个作为已知,求直线与平面所成的正弦值.
条件①:三棱锥的体积为;条件②:与圆台底面的夹角的正切值为.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
19.(12分)已知数列的前项和为,且.
(1)求及数列的通项公式;
(2)在与之间插入个数,使得这个数依次组成公差为的等差数列,求数列的前项和.
20.(12分)已知函数,.
(1)讨论的单调性;
(2)若,求证:.
21.(12分)西樵镇举办花市,如图,有一块半径为20米,圆心角的扇形展示台,展示台分成了四个区域:
三角形OCD摆放菊花“泥金香”,弓形CMD摆放菊花“紫龙卧雪”,扇形AOC和扇形BOD(其中)摆放菊花“朱砂红霜”.
预计这三种菊花展示带来的日效益分别是:泥金香50元/米2,紫龙卧雪30元/米2,朱砂红霜40元/米2.
(1)设,试建立日效益总量关于的函数关系式;
(2)试探求为何值时,日效益总量达到最大值.
22.(12分)已知函数,.
(1)求函数的单调区间;
(2)若,且,证明:.
佛山市南海区2022-2023学年高二下学期期中考试
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B C A C D A AD BCD AC ACD
13 14 15 16
0 1560 2
8.【答案】A【解析】令,,令,解得:;令,解得:;所以在上单调递减,在上单调递增,所以,所以,由可知,设,则在区间上是减函数.且.所以函数在区间上是增函数.所以,即.即:.故选:A.
11.【答案】AC【解析】由题意知:,则第3项的系数为,倒数第3项的系数为,则有即,∴.A选项正确;
可得,当时所有的有理项为,,,,即,,,.B选项错误;
设展开式中第项的系数最大,则,∴,故系数最大项为,系数最大项为第6项.C选项正确;
,第4项和第5项是二项式系数最大的项,D错误.故选:AC.
15.【答案】2【解析】设切点为,,则,解得.
令,则,所以当时,,单调递减;
当时,,单调递增.所以,所以方程的根为.
16.【答案】【解析】由,得.又,所以数列构成以2为首项,2为公比的等比数列,所以.又,累加得,即,所以.又因为满足上式,所以.
所以.因为,所以,
即,所以.故.
所以.
17.【解析】(1)设等差数列的公差为,由已知得,
即,
又,
解得(舍负),则,所以.
(2)结合(1)得,
则,
所以
.
18.【解析】(1)取AC中点M,连接,,如图,
由题意,,
又,.又,,
故,,
所以四边形为平行四边形,
则,又面,平面,故平面
(2)选①:,又平面ABC,
所以三棱锥体积.所以.
选②:因为平面,所以为与底面所成的角,所以,又,所以;
以为坐标原点,,,所在直线为坐标轴建立如图空间直角坐标系.
则有,,,,,
故,,
设平面的法向量,故
令,解得,得,
设所求角的大小为,则.
所以直线与平面PBC所成角的正弦值为.
19.【解析】(1)由题意,当时,,解得,
当时,,即,解得,
当时,由,可得,两式相减,可得,
整理,得,∴数列是以2为首项,2为公比的等比数列,
∴,.
(2)由(1)可得,,,在与之间插入个数,使得这个数依次组成公差为的等差数列,则有,∴,∴,
∴,
,
两式相减得,
∴.
20.【解析】(1),
当时,,,所以在上递增,在上递减
当时,或,,
此时在,上递增,在上递减;
当时,,所以在上递增;
当时,或,,
此时在,上递增,在上递减;
(2)当,,要证,只需证,令
则,,故在上递减,
又,,故存在,使得,即,即
且,,故在上递增,在上递减,
所以,
又,所以,所以,所以,
所以,所以时,.
【备注】此题可以使用切线放缩,即证明不等式.
21.【解析】(1)依题意得,,
则
,
其中,.
(2),令,得,
当,,函数递增,当时,,函数递减.
所以,是函数的极大值点,且唯一;从而当时,日效益总量可取得最大值.
22.【解析】(1),,
由得,当时,;当时,
∴在上单调递增,在上单调递减.
(2)∵,且,
∴由(1)知,不妨设.
要证,只需证明,而,在上单调递减,
故只需证明;又,
∴只需证明.
令函数,
则
.
当时,,,故,
∴在上单调递增,
故在上,
∴成立,故成立.
【极值点偏移·知识链接】①函数满足定义域内任意自变量都有,则函数关于直线对称;可以理解为函数在对称轴两侧,函数值变化快慢相同,且若为单峰函数,则
必为的极值点.
如二次函数的顶点就是极值点,若的两根的中点为,则刚好有,即极值点在两根的正中间,也就是极值点没有偏移.
②若相等变为不等,则为极值点偏移:若单峰函数的极值点为,且函数满足定义域内左侧的任意都有或,则函数极值点左右侧变化快慢不同.
故单峰函数定义域内任意不同的实数,满足,则与极值点必有确定的大小关系:
若,则称为极值点左偏.
若,则称为极值点右偏.
如:的极值点刚好在方程的两根中点的左边,我们称之为极值点左偏.
同课章节目录
