2023年安徽省名校联盟中考冲刺卷(一)数学试题(含答案)
文档属性
| 名称 | 2023年安徽省名校联盟中考冲刺卷(一)数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 508.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 00:00:00 | ||
图片预览


文档简介
2023年安徽省名校联盟中考冲刺卷(一)
数学试题
注意事项:
你拿到的试卷满分为150分,考试时间为120分钟。
本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
考试结束后,请将“试题卷”和“答题卷”一并收回。
第Ⅰ卷(选择题)
一.选择题(共10小题,满分40分,每小题4分)
1.的倒数是( )
A.5 B.﹣5 C.﹣ D.
2.2023年我国参加高考的考生人数预计约为1200万,这个数用科学记数法表示正确的是( )
A.1.2×106 B.12×106 C.1.2×107 D.0.12×107
3.一个几何体的主视图和左视图如图所示,则这个几何体可能是( )
A. B. C. D.
4.化简+的结果是( )
A.a﹣1 B.a+1 C.﹣a D.a
5.多项式x2﹣4xy﹣2y+x+4y2分解因式后有一个因式是x﹣2y,另一个因式是( )
A.x+2y+1 B.x+2y﹣1 C.x﹣2y+1 D.x﹣2y﹣1
6.下列命题中,是真命题的是( )
A.一组对边平行且有一组对边相等的四边形是平行四边形
B.对角线相等且互相垂直的四边形是正方形
C.有三个角相等的四边形是矩形
D.对角线互相垂直平分且有一组对角互补的四边形是正方形
7.已知关于x的一元二次方程x2﹣(3﹣k)x﹣2k+3=0有两个相等的实数根,则k的值为( )
A.﹣3 B.1 C.﹣1或3 D.﹣3或1
8.某校举办体能比赛,其中一项是引体向上,每完成一次记录1分,达到10个即为满分10分.甲、乙两班各出代表10个人,比赛成绩如下,根据表格中的信息判断,下列结论错误的是( )
甲班 7 8 9 7 10 10 9 10 10 10
乙班 10 8 7 9 8 10 10 9 10 9
A.甲班成绩的中位数是9.5分
B.乙班成绩的众数是10分
C.甲班的成绩较整齐
D.乙班成绩的平均数是9分
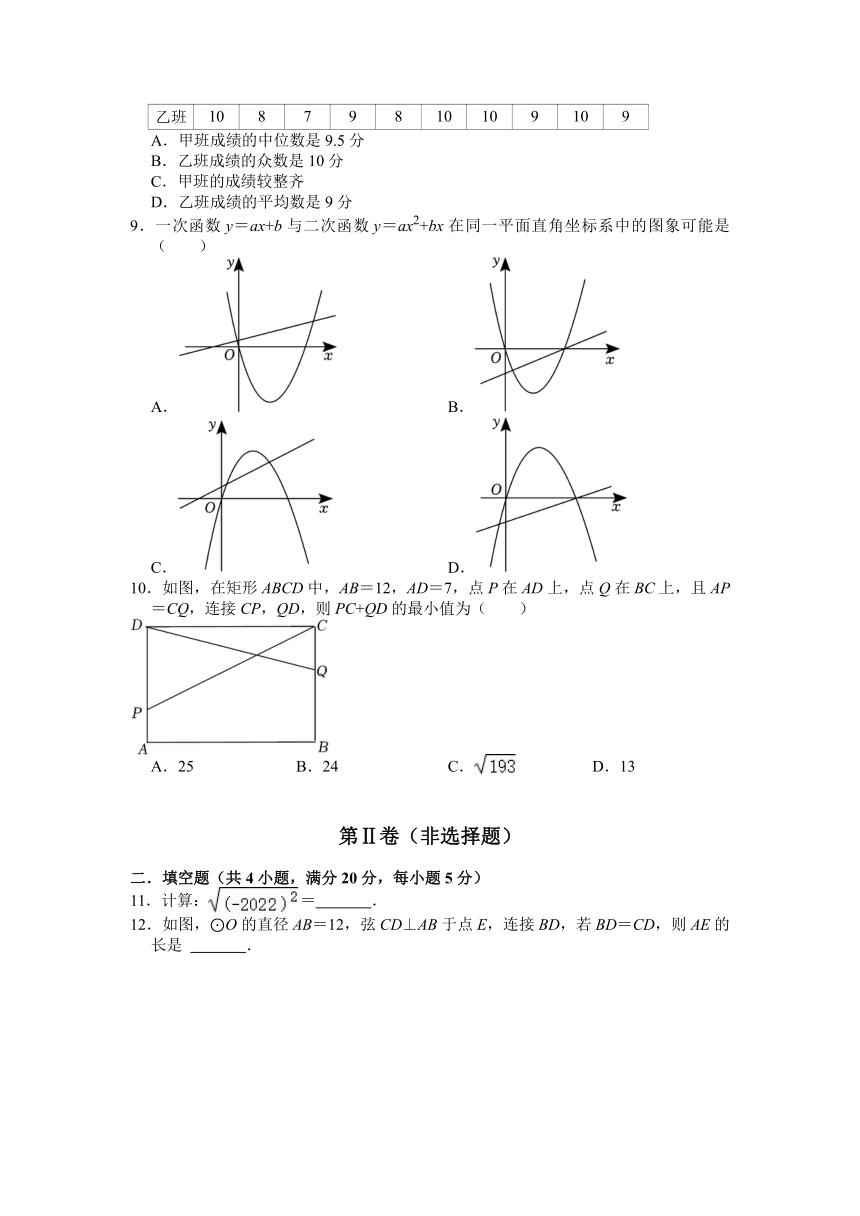
9.一次函数y=ax+b与二次函数y=ax2+bx在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
10.如图,在矩形ABCD中,AB=12,AD=7,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.25 B.24 C. D.13
第Ⅱ卷(非选择题)
二.填空题(共4小题,满分20分,每小题5分)
11.计算:= .
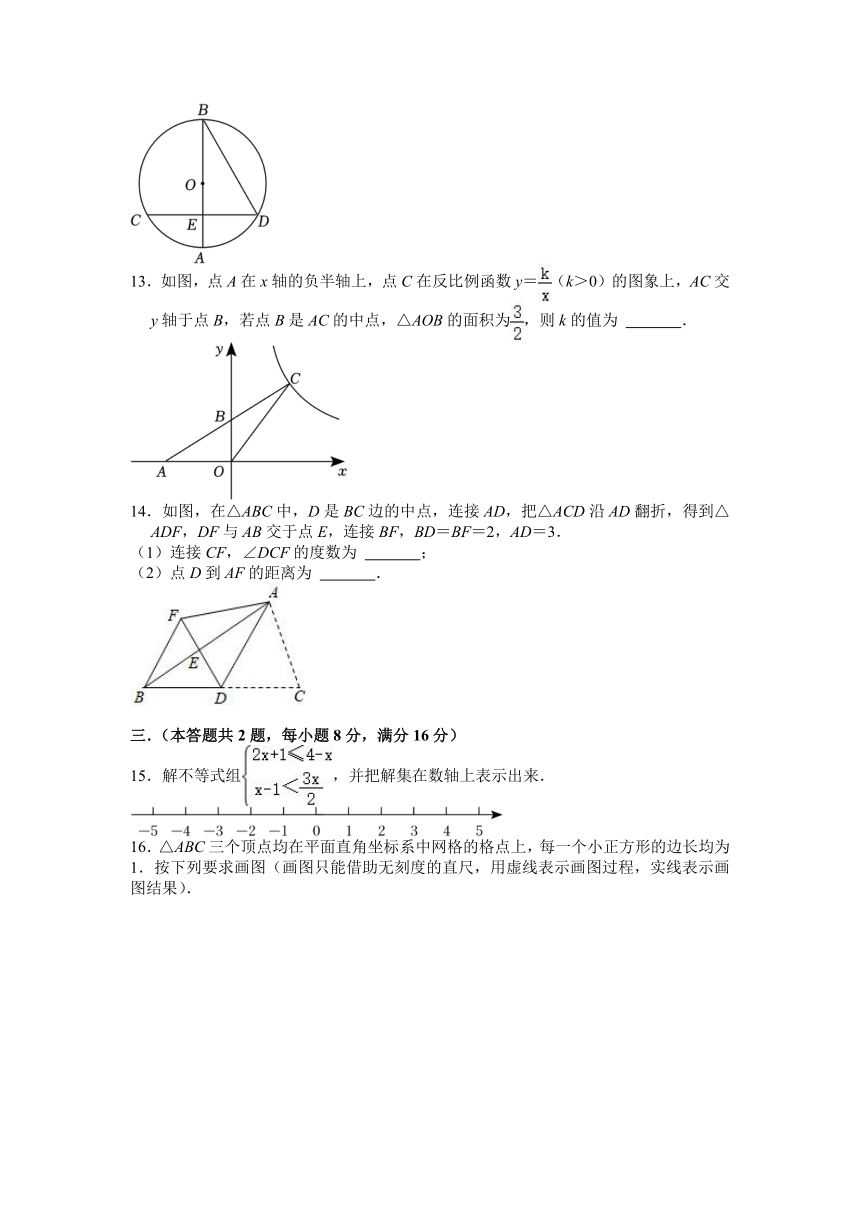
12.如图,⊙O的直径AB=12,弦CD⊥AB于点E,连接BD,若BD=CD,则AE的长是 .
13.如图,点A在x轴的负半轴上,点C在反比例函数y=(k>0)的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 .
14.如图,在△ABC中,D是BC边的中点,连接AD,把△ACD沿AD翻折,得到△ADF,DF与AB交于点E,连接BF,BD=BF=2,AD=3.
(1)连接CF,∠DCF的度数为 ;
(2)点D到AF的距离为 .
三.(本答题共2题,每小题8分,满分16分)
15.解不等式组,并把解集在数轴上表示出来.
16.△ABC三个顶点均在平面直角坐标系中网格的格点上,每一个小正方形的边长均为1.按下列要求画图(画图只能借助无刻度的直尺,用虚线表示画图过程,实线表示画图结果).
(1)把△ABC沿直线AC翻折,画出翻折后的△ACB1;
(2)找出格点D并画出直线AD,使直线AD将△ABC分成面积相等的两部分;
(3)在y轴上存在点P,使△BPC的面积等于3,直接写出点P的坐标.
四.(本答题共2题,每小题8分,满分16分)
17.《九章算术》是我国古代数学的经典北作,书中有这样一个记载:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”意思是:“甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后.甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?”试求黄金、白银每枚的重量.
18.很多代数公式都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式等.
【提出问题】如何用表示几何图形面积的方法计算:13+23+33+…+n3=?
【规律探究】观察如图表示几何图形面积的方法;
【解决问题】请用图中表示几何图形面积的方法写出13+23+33+…+n3= = (用含n的代数式表示);
【拓展应用】根据以上结论,计算:23+43+63+…+(2n)3的结果为 .
五.(本答题共2题,每小题10分,满分20分)
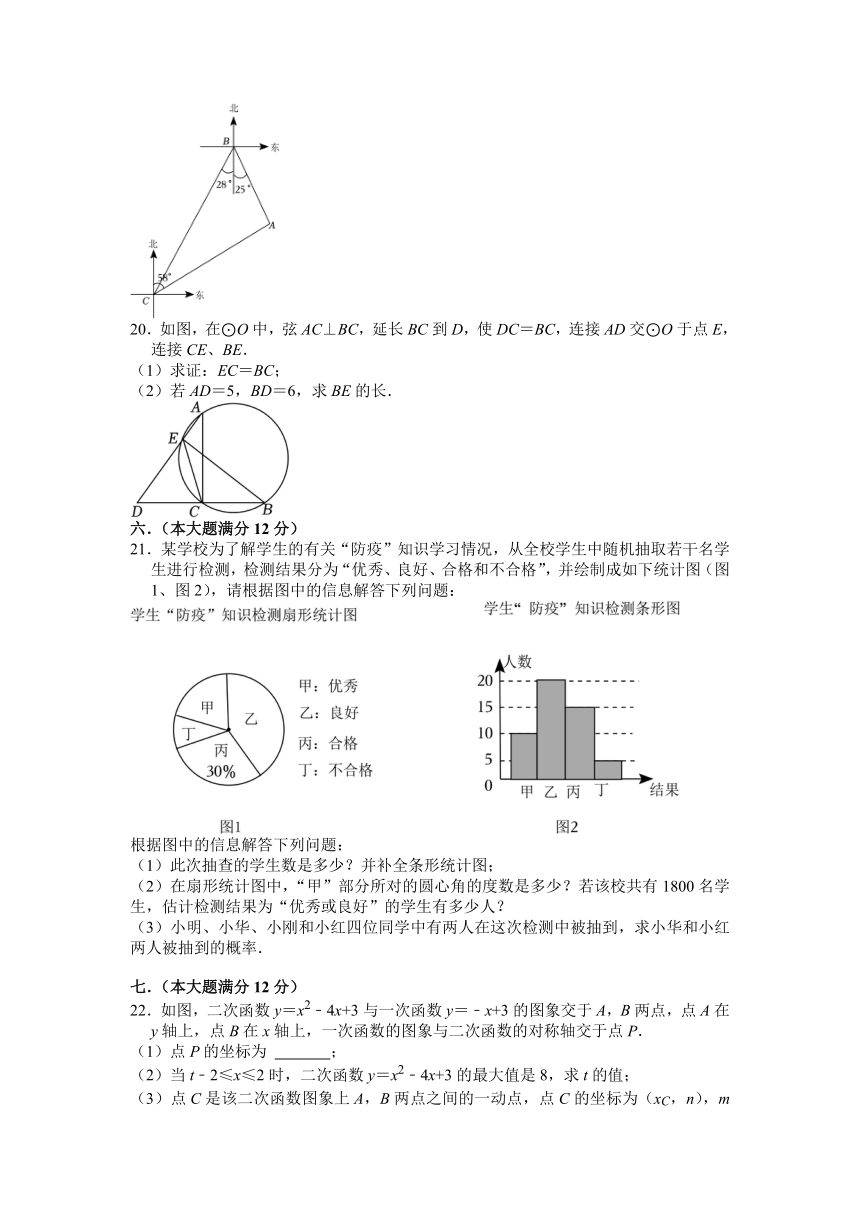
19.如图,某巡逻艇在海上例行巡逻,上午10时在C处接到海上搜救中心从B处发来的救援任务,此时事故船位于B处的南偏东25°方向上的A处,巡逻艇位于B处的南偏西28°方向上1260米处,事故船位于巡逻艇的北偏东58°方向上,巡逻艇立刻前往A处救援,已知巡逻艇每分钟行驶120米,请估计几分钟可以到达事故船A处.(结果保留整数.参考数据:≈1.73,sin53°≈,cos53°≈,tan53°≈).
20.如图,在⊙O中,弦AC⊥BC,延长BC到D,使DC=BC,连接AD交⊙O于点E,连接CE、BE.
(1)求证:EC=BC;
(2)若AD=5,BD=6,求BE的长.
六.(本大题满分12分)
21.某学校为了解学生的有关“防疫”知识学习情况,从全校学生中随机抽取若干名学生进行检测,检测结果分为“优秀、良好、合格和不合格”,并绘制成如下统计图(图1、图2),请根据图中的信息解答下列问题:
根据图中的信息解答下列问题:
(1)此次抽查的学生数是多少?并补全条形统计图;
(2)在扇形统计图中,“甲”部分所对的圆心角的度数是多少?若该校共有1800名学生,估计检测结果为“优秀或良好”的学生有多少人?
(3)小明、小华、小刚和小红四位同学中有两人在这次检测中被抽到,求小华和小红两人被抽到的概率.
七.(本大题满分12分)
22.如图,二次函数y=x2﹣4x+3与一次函数y=﹣x+3的图象交于A,B两点,点A在y轴上,点B在x轴上,一次函数的图象与二次函数的对称轴交于点P.
(1)点P的坐标为 ;
(2)当t﹣2≤x≤2时,二次函数y=x2﹣4x+3的最大值是8,求t的值;
(3)点C是该二次函数图象上A,B两点之间的一动点,点C的坐标为(xC,n),m=PC2,求当n取何值时,m的值最小,最小值是多少?
八.(本大题满分14分)
23.如图,已知:正方形ABCD中,AB=4,E为CD边中点,F为AD边中点,AE交BD于G,交BF于H,连接DH.
(1)求证:BG=2DG;
(2)求AH:HG:GE的值;
(3)求的值.
参考答案与试题解析
一、选择题
1.A 2.C 3.C 4.D 5.C 6.D 7.D 8.C 9.B 10.A
10.A
【解答】解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=12,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=24,BC=AD=7,
∴CE===25.
∴PC+PB的最小值为25.
故选:A.
二、填空题
11.2022 12.3. 13.6. 14.(1)30°;(2).
14.【解答】解:(1)连接CF,交AD于点M,
∵BD=BF=2,D是AC边上的中点,
∴BD=DC=2,
由翻折知,△ADC≌△ADF,AD垂直平分CF,
∴DC=DF=2,AC=AF,CM=FM,
∴BD=BF=DF=2,
∴△BDF为等边三角形,
∴∠BDF=∠BFD=∠FBC=60°,
∵DC=DF,
∴∠DCF=∠DFC=×60°=30°;
故答案为:30°;
(2)过点D作DH⊥AF于H,
在Rt△FDM中,∠DFC=30°,DF=2,
∴DM=1,FM=,
∴AM=AD﹣DM=3﹣1=2,
在Rt△AMF中,
AF==,
∵S△ADF=AF DH=AD CM,
∴DH=3×,
∴DH=.
故答案为:.
三、解答题
15.【答案】﹣2<x≤1.
【解答】解:,
由①得x≤1,
由②得:x>﹣2,
则不等式组的解集为﹣2<x≤1,
在数轴上表示:
.
16.【答案】(1)见解析;
(2)见解析;
(3)(0,0)或(0,4).
【解答】(1)解:如图,找到点B关于AC的对称点B1,连接AB1、B1C即可;
(2)如图,过点B作AC的平行线,取BD=AC,作直线AD,则直线AD将△ABC分成面积相等的两部分;
(3)如图,设BC交y轴于点Q,由图可知点Q(0,2),
设点B到y轴的距离为h1,点C到y轴的距离为h2,由图可知h1=2,h2=1,
则S△BPC=S△BPQ+S△CPQ===
∵△BPC的面积等于3,即,
解得PQ=2,
∴点P的坐标为(0,0)或(0,4).
17.【答案】黄金每枚重两,白银每枚重两.
【解答】解:设黄金每枚重x两,则白银每枚重y两,根据题意列方程得,
解:.
解得.
答:黄金每枚重两,白银每枚重两.
18.【答案】【规律探究】62;
【解决问题】;
【拓展应用】2n2(n+1)2或2n4+4n3+2n2.
【解答】解:【规律探究】由题意可得13+23+33=(1+2+3)2=62;
【解决问题】由13+23+33+…+n3=(1+2+3+…+n)2=[]2=,
故答案为:;
【拓展应用】由题意得23+43+63+…+(2n)3=23×13+23×23+23×33+…+23×n3=23×(13+23+33+…+n3)=8×[]=2n2(n+1)2或2n4+4n3+2n2,
故答案为:2n2(n+1)2或2n4+4n3+2n2.
19.【答案】估计8分钟可以到达事故船A处.
【解答】解:过点A作AD⊥BC,垂足为D,
由题意得:
BC=1260米,∠ABD=28°+25°=53°,∠ACB=58°﹣28°=30°,
设AD=x米,
在Rt△ABD中,BD=≈=x(米),
在Rt△ADC中,CD===x(米),
∵CD+BD=BC,
∴x+x=1260,
解得:x≈508.1,
∴AD≈508.1米,
在Rt△ADC中,∠ACD=30°,
∴AC=2AD=1016.2(米),
∴1016.2÷120≈8(分钟),
∴估计8分钟可以到达事故船A处.
20.【答案】见试题解答内容
【解答】(1)证明:∵弦AC⊥BC,
∴∠ACB=90°,
∴∠AEB=∠ACB=90°,
∴∠DEB=180°﹣∠AEB=90°,
∵DC=BC,
∴EC=BD,
∴EC=BC;
(2)解:∵CD=BC,BD=6,
∴CD=BD=3,
∵∠ACD=180°﹣∠ACB=90°,AD=5,
∴AC===4,
∵sin∠BDE=sin∠ADC,
∴=,
∴=,
∴BE=.
21.【答案】(1)50人;画图见解答.
(2)72°;1080人.
(3).
【解答】解:(1)此次抽查的学生数是15÷30%=50(人).
补全条形统计图如下.
(2)扇形统计图中,“甲”部分所对的圆心角的度数为360°×=72°.
估计检测结果为“优秀或良好”的学生有1800×=1080(人).
(3)将小明、小华、小刚和小红分别记为A,B,C,D,
画树状图如下:
共有12种等可能的结果,其中小华和小红两人被抽到的结果有2种,
∴小华和小红两人被抽到的概率为=.
22.【答案】(1)(2,1);
(2)t=1;
(3)当时,m的值最小,最小值是.
【解答】解:(1)∵二次函数y=x2﹣4x+3的对称轴为直线x=﹣=2,
把x=2代入y=﹣x+3得y=﹣2+3=1,
∴点P的坐标为(2,1),
故答案为:(2,1);
(2)∵二次函数的对称轴为x=2,在对称轴左侧二次函数y的值随x的增大而减小,
∴二次函数y=x2﹣4x+3的最大值是8,
即(t﹣2)2﹣4(t﹣2)+3=8,
解得t=1,t=7,
∵t﹣2≤x≤2,
∴t≤4,
∴t=7(舍去),
即t=1;
(3)∵C(xC,n)在抛物线上,
∴n=x﹣4xC+3,
∴m=PC2=(2﹣xC)2+(1﹣n)2=xC2﹣4xC+4+n2﹣2n+1=xC2﹣4xC+3+1+n2﹣2n+1=n+1+n2﹣2n+1=n2﹣n+2=(n﹣)2+,
∵1>0,
当时,m的值最小,最小值是.
23.【答案】见试题解答内容
【解答】(1)证明:∵四边形ABCD是正方形,
∵AB∥CD,AB=CD,
∵DE=CE,
∴==,
∴BG=2DG.
(2)解:∵AB∥CD,AB=CD,
∵DE=CE,
∴===,
在Rt△ADE中,∵AD=4,DE=2,
∴AE=2,
∴EG=,
同法可得BF=2,
∵AB=AD,∠BAF=∠ADE,AF=DE,
∴△BAF≌△ADE,
∴∠ABF=∠DAE,
∵∠DAE+∠BAH=90°,
∴∠ABF+∠BAH=90°,
∴∠AHB=90°,
∴AE⊥BF,
∴AH===,
∴HG=2﹣﹣=,
∴AH:HG:GE=::=6:4:5.
(3)作DM⊥AE于M.
由(2)可知:DM=AH=,
∴EM==,
∴HM=EH﹣EM=,
∴DH=,
∵BH==,
∴==.
数学试题
注意事项:
你拿到的试卷满分为150分,考试时间为120分钟。
本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
考试结束后,请将“试题卷”和“答题卷”一并收回。
第Ⅰ卷(选择题)
一.选择题(共10小题,满分40分,每小题4分)
1.的倒数是( )
A.5 B.﹣5 C.﹣ D.
2.2023年我国参加高考的考生人数预计约为1200万,这个数用科学记数法表示正确的是( )
A.1.2×106 B.12×106 C.1.2×107 D.0.12×107
3.一个几何体的主视图和左视图如图所示,则这个几何体可能是( )
A. B. C. D.
4.化简+的结果是( )
A.a﹣1 B.a+1 C.﹣a D.a
5.多项式x2﹣4xy﹣2y+x+4y2分解因式后有一个因式是x﹣2y,另一个因式是( )
A.x+2y+1 B.x+2y﹣1 C.x﹣2y+1 D.x﹣2y﹣1
6.下列命题中,是真命题的是( )
A.一组对边平行且有一组对边相等的四边形是平行四边形
B.对角线相等且互相垂直的四边形是正方形
C.有三个角相等的四边形是矩形
D.对角线互相垂直平分且有一组对角互补的四边形是正方形
7.已知关于x的一元二次方程x2﹣(3﹣k)x﹣2k+3=0有两个相等的实数根,则k的值为( )
A.﹣3 B.1 C.﹣1或3 D.﹣3或1
8.某校举办体能比赛,其中一项是引体向上,每完成一次记录1分,达到10个即为满分10分.甲、乙两班各出代表10个人,比赛成绩如下,根据表格中的信息判断,下列结论错误的是( )
甲班 7 8 9 7 10 10 9 10 10 10
乙班 10 8 7 9 8 10 10 9 10 9
A.甲班成绩的中位数是9.5分
B.乙班成绩的众数是10分
C.甲班的成绩较整齐
D.乙班成绩的平均数是9分
9.一次函数y=ax+b与二次函数y=ax2+bx在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
10.如图,在矩形ABCD中,AB=12,AD=7,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为( )
A.25 B.24 C. D.13
第Ⅱ卷(非选择题)
二.填空题(共4小题,满分20分,每小题5分)
11.计算:= .
12.如图,⊙O的直径AB=12,弦CD⊥AB于点E,连接BD,若BD=CD,则AE的长是 .
13.如图,点A在x轴的负半轴上,点C在反比例函数y=(k>0)的图象上,AC交y轴于点B,若点B是AC的中点,△AOB的面积为,则k的值为 .
14.如图,在△ABC中,D是BC边的中点,连接AD,把△ACD沿AD翻折,得到△ADF,DF与AB交于点E,连接BF,BD=BF=2,AD=3.
(1)连接CF,∠DCF的度数为 ;
(2)点D到AF的距离为 .
三.(本答题共2题,每小题8分,满分16分)
15.解不等式组,并把解集在数轴上表示出来.
16.△ABC三个顶点均在平面直角坐标系中网格的格点上,每一个小正方形的边长均为1.按下列要求画图(画图只能借助无刻度的直尺,用虚线表示画图过程,实线表示画图结果).
(1)把△ABC沿直线AC翻折,画出翻折后的△ACB1;
(2)找出格点D并画出直线AD,使直线AD将△ABC分成面积相等的两部分;
(3)在y轴上存在点P,使△BPC的面积等于3,直接写出点P的坐标.
四.(本答题共2题,每小题8分,满分16分)
17.《九章算术》是我国古代数学的经典北作,书中有这样一个记载:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”意思是:“甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后.甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?”试求黄金、白银每枚的重量.
18.很多代数公式都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式等.
【提出问题】如何用表示几何图形面积的方法计算:13+23+33+…+n3=?
【规律探究】观察如图表示几何图形面积的方法;
【解决问题】请用图中表示几何图形面积的方法写出13+23+33+…+n3= = (用含n的代数式表示);
【拓展应用】根据以上结论,计算:23+43+63+…+(2n)3的结果为 .
五.(本答题共2题,每小题10分,满分20分)
19.如图,某巡逻艇在海上例行巡逻,上午10时在C处接到海上搜救中心从B处发来的救援任务,此时事故船位于B处的南偏东25°方向上的A处,巡逻艇位于B处的南偏西28°方向上1260米处,事故船位于巡逻艇的北偏东58°方向上,巡逻艇立刻前往A处救援,已知巡逻艇每分钟行驶120米,请估计几分钟可以到达事故船A处.(结果保留整数.参考数据:≈1.73,sin53°≈,cos53°≈,tan53°≈).
20.如图,在⊙O中,弦AC⊥BC,延长BC到D,使DC=BC,连接AD交⊙O于点E,连接CE、BE.
(1)求证:EC=BC;
(2)若AD=5,BD=6,求BE的长.
六.(本大题满分12分)
21.某学校为了解学生的有关“防疫”知识学习情况,从全校学生中随机抽取若干名学生进行检测,检测结果分为“优秀、良好、合格和不合格”,并绘制成如下统计图(图1、图2),请根据图中的信息解答下列问题:
根据图中的信息解答下列问题:
(1)此次抽查的学生数是多少?并补全条形统计图;
(2)在扇形统计图中,“甲”部分所对的圆心角的度数是多少?若该校共有1800名学生,估计检测结果为“优秀或良好”的学生有多少人?
(3)小明、小华、小刚和小红四位同学中有两人在这次检测中被抽到,求小华和小红两人被抽到的概率.
七.(本大题满分12分)
22.如图,二次函数y=x2﹣4x+3与一次函数y=﹣x+3的图象交于A,B两点,点A在y轴上,点B在x轴上,一次函数的图象与二次函数的对称轴交于点P.
(1)点P的坐标为 ;
(2)当t﹣2≤x≤2时,二次函数y=x2﹣4x+3的最大值是8,求t的值;
(3)点C是该二次函数图象上A,B两点之间的一动点,点C的坐标为(xC,n),m=PC2,求当n取何值时,m的值最小,最小值是多少?
八.(本大题满分14分)
23.如图,已知:正方形ABCD中,AB=4,E为CD边中点,F为AD边中点,AE交BD于G,交BF于H,连接DH.
(1)求证:BG=2DG;
(2)求AH:HG:GE的值;
(3)求的值.
参考答案与试题解析
一、选择题
1.A 2.C 3.C 4.D 5.C 6.D 7.D 8.C 9.B 10.A
10.A
【解答】解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC,
∵AP=CQ,
∴AD﹣AP=BC﹣CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=12,连接PE,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∵BE=2AB=24,BC=AD=7,
∴CE===25.
∴PC+PB的最小值为25.
故选:A.
二、填空题
11.2022 12.3. 13.6. 14.(1)30°;(2).
14.【解答】解:(1)连接CF,交AD于点M,
∵BD=BF=2,D是AC边上的中点,
∴BD=DC=2,
由翻折知,△ADC≌△ADF,AD垂直平分CF,
∴DC=DF=2,AC=AF,CM=FM,
∴BD=BF=DF=2,
∴△BDF为等边三角形,
∴∠BDF=∠BFD=∠FBC=60°,
∵DC=DF,
∴∠DCF=∠DFC=×60°=30°;
故答案为:30°;
(2)过点D作DH⊥AF于H,
在Rt△FDM中,∠DFC=30°,DF=2,
∴DM=1,FM=,
∴AM=AD﹣DM=3﹣1=2,
在Rt△AMF中,
AF==,
∵S△ADF=AF DH=AD CM,
∴DH=3×,
∴DH=.
故答案为:.
三、解答题
15.【答案】﹣2<x≤1.
【解答】解:,
由①得x≤1,
由②得:x>﹣2,
则不等式组的解集为﹣2<x≤1,
在数轴上表示:
.
16.【答案】(1)见解析;
(2)见解析;
(3)(0,0)或(0,4).
【解答】(1)解:如图,找到点B关于AC的对称点B1,连接AB1、B1C即可;
(2)如图,过点B作AC的平行线,取BD=AC,作直线AD,则直线AD将△ABC分成面积相等的两部分;
(3)如图,设BC交y轴于点Q,由图可知点Q(0,2),
设点B到y轴的距离为h1,点C到y轴的距离为h2,由图可知h1=2,h2=1,
则S△BPC=S△BPQ+S△CPQ===
∵△BPC的面积等于3,即,
解得PQ=2,
∴点P的坐标为(0,0)或(0,4).
17.【答案】黄金每枚重两,白银每枚重两.
【解答】解:设黄金每枚重x两,则白银每枚重y两,根据题意列方程得,
解:.
解得.
答:黄金每枚重两,白银每枚重两.
18.【答案】【规律探究】62;
【解决问题】;
【拓展应用】2n2(n+1)2或2n4+4n3+2n2.
【解答】解:【规律探究】由题意可得13+23+33=(1+2+3)2=62;
【解决问题】由13+23+33+…+n3=(1+2+3+…+n)2=[]2=,
故答案为:;
【拓展应用】由题意得23+43+63+…+(2n)3=23×13+23×23+23×33+…+23×n3=23×(13+23+33+…+n3)=8×[]=2n2(n+1)2或2n4+4n3+2n2,
故答案为:2n2(n+1)2或2n4+4n3+2n2.
19.【答案】估计8分钟可以到达事故船A处.
【解答】解:过点A作AD⊥BC,垂足为D,
由题意得:
BC=1260米,∠ABD=28°+25°=53°,∠ACB=58°﹣28°=30°,
设AD=x米,
在Rt△ABD中,BD=≈=x(米),
在Rt△ADC中,CD===x(米),
∵CD+BD=BC,
∴x+x=1260,
解得:x≈508.1,
∴AD≈508.1米,
在Rt△ADC中,∠ACD=30°,
∴AC=2AD=1016.2(米),
∴1016.2÷120≈8(分钟),
∴估计8分钟可以到达事故船A处.
20.【答案】见试题解答内容
【解答】(1)证明:∵弦AC⊥BC,
∴∠ACB=90°,
∴∠AEB=∠ACB=90°,
∴∠DEB=180°﹣∠AEB=90°,
∵DC=BC,
∴EC=BD,
∴EC=BC;
(2)解:∵CD=BC,BD=6,
∴CD=BD=3,
∵∠ACD=180°﹣∠ACB=90°,AD=5,
∴AC===4,
∵sin∠BDE=sin∠ADC,
∴=,
∴=,
∴BE=.
21.【答案】(1)50人;画图见解答.
(2)72°;1080人.
(3).
【解答】解:(1)此次抽查的学生数是15÷30%=50(人).
补全条形统计图如下.
(2)扇形统计图中,“甲”部分所对的圆心角的度数为360°×=72°.
估计检测结果为“优秀或良好”的学生有1800×=1080(人).
(3)将小明、小华、小刚和小红分别记为A,B,C,D,
画树状图如下:
共有12种等可能的结果,其中小华和小红两人被抽到的结果有2种,
∴小华和小红两人被抽到的概率为=.
22.【答案】(1)(2,1);
(2)t=1;
(3)当时,m的值最小,最小值是.
【解答】解:(1)∵二次函数y=x2﹣4x+3的对称轴为直线x=﹣=2,
把x=2代入y=﹣x+3得y=﹣2+3=1,
∴点P的坐标为(2,1),
故答案为:(2,1);
(2)∵二次函数的对称轴为x=2,在对称轴左侧二次函数y的值随x的增大而减小,
∴二次函数y=x2﹣4x+3的最大值是8,
即(t﹣2)2﹣4(t﹣2)+3=8,
解得t=1,t=7,
∵t﹣2≤x≤2,
∴t≤4,
∴t=7(舍去),
即t=1;
(3)∵C(xC,n)在抛物线上,
∴n=x﹣4xC+3,
∴m=PC2=(2﹣xC)2+(1﹣n)2=xC2﹣4xC+4+n2﹣2n+1=xC2﹣4xC+3+1+n2﹣2n+1=n+1+n2﹣2n+1=n2﹣n+2=(n﹣)2+,
∵1>0,
当时,m的值最小,最小值是.
23.【答案】见试题解答内容
【解答】(1)证明:∵四边形ABCD是正方形,
∵AB∥CD,AB=CD,
∵DE=CE,
∴==,
∴BG=2DG.
(2)解:∵AB∥CD,AB=CD,
∵DE=CE,
∴===,
在Rt△ADE中,∵AD=4,DE=2,
∴AE=2,
∴EG=,
同法可得BF=2,
∵AB=AD,∠BAF=∠ADE,AF=DE,
∴△BAF≌△ADE,
∴∠ABF=∠DAE,
∵∠DAE+∠BAH=90°,
∴∠ABF+∠BAH=90°,
∴∠AHB=90°,
∴AE⊥BF,
∴AH===,
∴HG=2﹣﹣=,
∴AH:HG:GE=::=6:4:5.
(3)作DM⊥AE于M.
由(2)可知:DM=AH=,
∴EM==,
∴HM=EH﹣EM=,
∴DH=,
∵BH==,
∴==.
同课章节目录
