20.1.2 中位数和众数(2)课件(共31张PPT)
文档属性
| 名称 | 20.1.2 中位数和众数(2)课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 00:12:17 | ||
图片预览











文档简介
(共31张PPT)
20.1.2 中位数和众数(2)
人教版八年级下册
第2课时 平均数、中位数和众数的应用
知识回顾
1.某校八年级(2)班6名女同学的体重(单位:kg)分别为35,36,38,40,42,42,则这组数据的中位数是( )
A.38 B.39 C.40 D.42
中位数:将一组数据按照由 (或由 )的顺序排列,如果数据的个数是奇数,则处于 位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的 就是这组数据的中位数.
小到大
大到小
中间
平均数
B
知识回顾
2.在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵数分别是3,1,1,3,2,3,2,则这组数据中的中位数和众数分别是( )
A.3,2 B.2,3 C.2,2 D.3,3
众数:一组数据中出现次数 的数据就是这组数据的众数.如果一组数据中有两个数据的频数相同,都是最大,那么这两个数据 这组数据的众数.
最多
都是
B
教学目标
1.进一步认识平均数、中位数、众数都可以反映一组数据的集中趋势;
2.了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.
新知导入
某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 职员G
月工资/元 6000 4000 1700 1300 1200 1100 1100 1100 500
经理说:“我公司员工收入很高,月平均工资为2000元.”
职员C说:“我的工资是1200元,在公司算中等收入.”
职员D说:“我们好几个人工资都是1100元.”
一位应聘者心里在琢磨,这个公司员工收入到底怎样呢?
新知探究
例1 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
新知探究
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
思考
新知探究
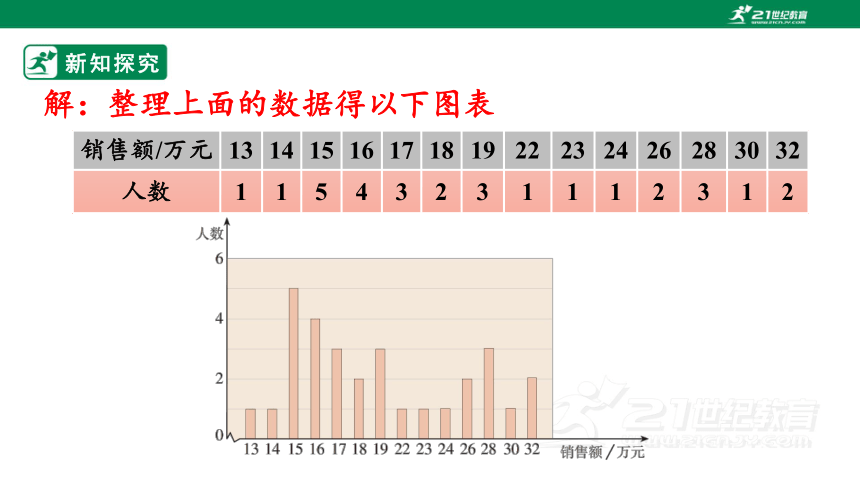
解:整理上面的数据得以下图表
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
新知探究
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:样本数据的众数是_____,中位数是_____,利用计算器求得这组数据的平均数约是_____.
可以推测,这个服装部营业员的月销售额为_____万元的人数最多,中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
新知探究
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
20
20
大
三分之一
新知探究
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:月销售额可以定为每月____万元(中位数).因为从样本情况看,月销售额在____万元以上(含18万元)的有16人,占总人数的一半左右.可以估计,如果月销售额定为____万元,将有一半左右的营业员获得奖励.
18
18
18
新知小结
平均数、中位数和众数的联系与区别
平均数 1.优点:跟每个数据都有关系,常用样本的平均数估计总体的平均数. 2.缺点:易受 的影响.
中位数 1.优点:不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述集中趋势. 2.缺点:不能充分地利用各数据.
极端值
新知小结
众数 1.优点:其考察的是各数据出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映出问题的实质. 2.缺点:当各数据重复出现的次数大致相等时,研究众数就没什么意义了.
三者的联系:(1)都能体现一组数据的集中趋势;
(2)实际问题中求得的平均数、中位数和众数的单位与原数据的单位一致.
新知典例
例2 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
新知探究
(2)这三个厂家推销广告分别用了哪一种表示集中趋势的特征数?
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
解:甲厂选用平均数8;
乙厂选用众数8;
丙厂选用中位数8;
新知探究
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
解:宜选购乙厂的产品;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
因为乙厂产品、平均使用寿命最长且多数超过8年或达到8年寿命.
新知典例
例3 某中学开展演讲比赛活动,八(1)、八(2)班根据初赛成绩各选5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
新知典例
(1)根据下图填写下表:
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85
八(2)班 85 80
85
100
新知典例
解:∵两班的平均数相同,八(1)班的中位数较高,
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
∴八(1)班的复赛成绩较好;
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85 85
八(2)班 85 80 100
新知典例
解:∵八(1)班、八(2)班前两名选手的平均分分别为92.5分、100分,
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强?
∴在每班参加复赛的选手中分别选出2人参加决赛,
∴八(2)班的实力更强.
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85 85
八(2)班 85 80 100
新知练习
码号 33 34 35 36 37
人数 7 6 15 1 1
1.抽样调查了某班30位女生所穿鞋子的尺码,数据如下(单位:码).在这组数据的平均数、中位数和众数中,鞋厂最感兴趣的是( )
A.平均数 B.中位数
C.众数 D.无法确定
C
新知典例
2.小明最近6次测验的成绩依次为:90分,85分,70分,65分,85分,75分.
(1)这6次测验成绩的平均数、中位数和众数分别是多少?
(2)如果他希望告诉别人他的成绩不错,那么他会选用哪个数表示他的成绩?
解:(1)平均数:
=(90+85+70+65+85+75)÷6 ≈78.3
x
_
中位数:(85+75)÷2=80
众数为85
(2)小明会选择众数来表示自己的成绩不错.
课堂总结
知识点:平均数、中位数和众数的应用
1.平均数、中位数、众数都刻画了数据的 .
2.平均数能充分利用数据提供的信息,反映 ,在实际中它易受“极端值”的影响.
3.中位数的计算简单,不受 影响,但不能充分利用所有数据.
4.当一组数据某一数值不断重复出现时,众数就成了人们关心的量,它不受 影响.
集中趋势
平均水平
极端值
极端值
课堂练习
1.据调查,某班20位女同学所穿鞋子的尺码如表所示,则鞋子尺码的众数和中位数分别是( )
尺码(码) 34 35 36 37 38
人数 2 5 10 2 1
A.35码,35码 B.35码,36码
C.36码,35码 D.36码,36码
D
课堂练习
2.某次数学测验中,五位同学的分数分别是:89,91,105,105,110.这组数据的中位数是 ,众数是 ,平均数是 .
3.为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查.那么最终决定买什么水果,最值得关注的应该是统计调查数据的 (填“中位数”“平均数”或“众数”).
105
105
100
众数
课堂练习
4.某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
课堂练习
请根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
2
25-6-12-5=2(人),如图所示.
课堂练习
(2)直接写出表格中a,b,c的值;
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
a=87.6,b=90,c=100
课堂练习
解:①一班和二班平均数相同,一班的中位数大于二班的中位数,故一班的成绩好于二班;②一班和二班平均数相同,一班的众数小于二班的众数,故二班的成绩好于一班;③B级以上(包括B级)一班18人,二班12人,故一班的成绩好于二班.
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:①从平均数和中位数方面来比较一班和二班的成绩;②从平均数和众数方面来比较一班和二班的成绩;③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
20.1.2 中位数和众数(2)
人教版八年级下册
第2课时 平均数、中位数和众数的应用
知识回顾
1.某校八年级(2)班6名女同学的体重(单位:kg)分别为35,36,38,40,42,42,则这组数据的中位数是( )
A.38 B.39 C.40 D.42
中位数:将一组数据按照由 (或由 )的顺序排列,如果数据的个数是奇数,则处于 位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的 就是这组数据的中位数.
小到大
大到小
中间
平均数
B
知识回顾
2.在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵数分别是3,1,1,3,2,3,2,则这组数据中的中位数和众数分别是( )
A.3,2 B.2,3 C.2,2 D.3,3
众数:一组数据中出现次数 的数据就是这组数据的众数.如果一组数据中有两个数据的频数相同,都是最大,那么这两个数据 这组数据的众数.
最多
都是
B
教学目标
1.进一步认识平均数、中位数、众数都可以反映一组数据的集中趋势;
2.了解平均数、中位数、众数各自的特点,能选择适当的量反映数据的集中趋势.
新知导入
某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 职员G
月工资/元 6000 4000 1700 1300 1200 1100 1100 1100 500
经理说:“我公司员工收入很高,月平均工资为2000元.”
职员C说:“我的工资是1200元,在公司算中等收入.”
职员D说:“我们好几个人工资都是1100元.”
一位应聘者心里在琢磨,这个公司员工收入到底怎样呢?
新知探究
例1 某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
新知探究
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
思考
新知探究
解:整理上面的数据得以下图表
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
新知探究
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:样本数据的众数是_____,中位数是_____,利用计算器求得这组数据的平均数约是_____.
可以推测,这个服装部营业员的月销售额为_____万元的人数最多,中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
新知探究
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
20
20
大
三分之一
新知探究
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
解:月销售额可以定为每月____万元(中位数).因为从样本情况看,月销售额在____万元以上(含18万元)的有16人,占总人数的一半左右.可以估计,如果月销售额定为____万元,将有一半左右的营业员获得奖励.
18
18
18
新知小结
平均数、中位数和众数的联系与区别
平均数 1.优点:跟每个数据都有关系,常用样本的平均数估计总体的平均数. 2.缺点:易受 的影响.
中位数 1.优点:不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述集中趋势. 2.缺点:不能充分地利用各数据.
极端值
新知小结
众数 1.优点:其考察的是各数据出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映出问题的实质. 2.缺点:当各数据重复出现的次数大致相等时,研究众数就没什么意义了.
三者的联系:(1)都能体现一组数据的集中趋势;
(2)实际问题中求得的平均数、中位数和众数的单位与原数据的单位一致.
新知典例
例2 甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
新知探究
(2)这三个厂家推销广告分别用了哪一种表示集中趋势的特征数?
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
解:甲厂选用平均数8;
乙厂选用众数8;
丙厂选用中位数8;
新知探究
(3)如果你是顾客,宜选购哪家工厂的产品?为什么?
解:宜选购乙厂的产品;
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
因为乙厂产品、平均使用寿命最长且多数超过8年或达到8年寿命.
新知典例
例3 某中学开展演讲比赛活动,八(1)、八(2)班根据初赛成绩各选5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
新知典例
(1)根据下图填写下表:
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85
八(2)班 85 80
85
100
新知典例
解:∵两班的平均数相同,八(1)班的中位数较高,
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
∴八(1)班的复赛成绩较好;
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85 85
八(2)班 85 80 100
新知典例
解:∵八(1)班、八(2)班前两名选手的平均分分别为92.5分、100分,
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强?
∴在每班参加复赛的选手中分别选出2人参加决赛,
∴八(2)班的实力更强.
平均分(分) 中位数(分) 众数(分)
八(1)班 85 85 85
八(2)班 85 80 100
新知练习
码号 33 34 35 36 37
人数 7 6 15 1 1
1.抽样调查了某班30位女生所穿鞋子的尺码,数据如下(单位:码).在这组数据的平均数、中位数和众数中,鞋厂最感兴趣的是( )
A.平均数 B.中位数
C.众数 D.无法确定
C
新知典例
2.小明最近6次测验的成绩依次为:90分,85分,70分,65分,85分,75分.
(1)这6次测验成绩的平均数、中位数和众数分别是多少?
(2)如果他希望告诉别人他的成绩不错,那么他会选用哪个数表示他的成绩?
解:(1)平均数:
=(90+85+70+65+85+75)÷6 ≈78.3
x
_
中位数:(85+75)÷2=80
众数为85
(2)小明会选择众数来表示自己的成绩不错.
课堂总结
知识点:平均数、中位数和众数的应用
1.平均数、中位数、众数都刻画了数据的 .
2.平均数能充分利用数据提供的信息,反映 ,在实际中它易受“极端值”的影响.
3.中位数的计算简单,不受 影响,但不能充分利用所有数据.
4.当一组数据某一数值不断重复出现时,众数就成了人们关心的量,它不受 影响.
集中趋势
平均水平
极端值
极端值
课堂练习
1.据调查,某班20位女同学所穿鞋子的尺码如表所示,则鞋子尺码的众数和中位数分别是( )
尺码(码) 34 35 36 37 38
人数 2 5 10 2 1
A.35码,35码 B.35码,36码
C.36码,35码 D.36码,36码
D
课堂练习
2.某次数学测验中,五位同学的分数分别是:89,91,105,105,110.这组数据的中位数是 ,众数是 ,平均数是 .
3.为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查.那么最终决定买什么水果,最值得关注的应该是统计调查数据的 (填“中位数”“平均数”或“众数”).
105
105
100
众数
课堂练习
4.某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
课堂练习
请根据以上提供的信息解答下列问题:
(1)把一班竞赛成绩统计图补充完整;
2
25-6-12-5=2(人),如图所示.
课堂练习
(2)直接写出表格中a,b,c的值;
平均数(分) 中位数(分) 众数(分)
一班 a b 90
二班 87.6 80 c
a=87.6,b=90,c=100
课堂练习
解:①一班和二班平均数相同,一班的中位数大于二班的中位数,故一班的成绩好于二班;②一班和二班平均数相同,一班的众数小于二班的众数,故二班的成绩好于一班;③B级以上(包括B级)一班18人,二班12人,故一班的成绩好于二班.
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:①从平均数和中位数方面来比较一班和二班的成绩;②从平均数和众数方面来比较一班和二班的成绩;③从B级以上(包括B级)的人数方面来比较一班和二班的成绩.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
