根与系数的关系[上学期]
图片预览






文档简介
(共17张PPT)
一元二次方程根与系数的关系
一元二次方程 ax2+bx+c=0(a≠0) 的求根公式:
X=
(b2-4ac≥ 0)
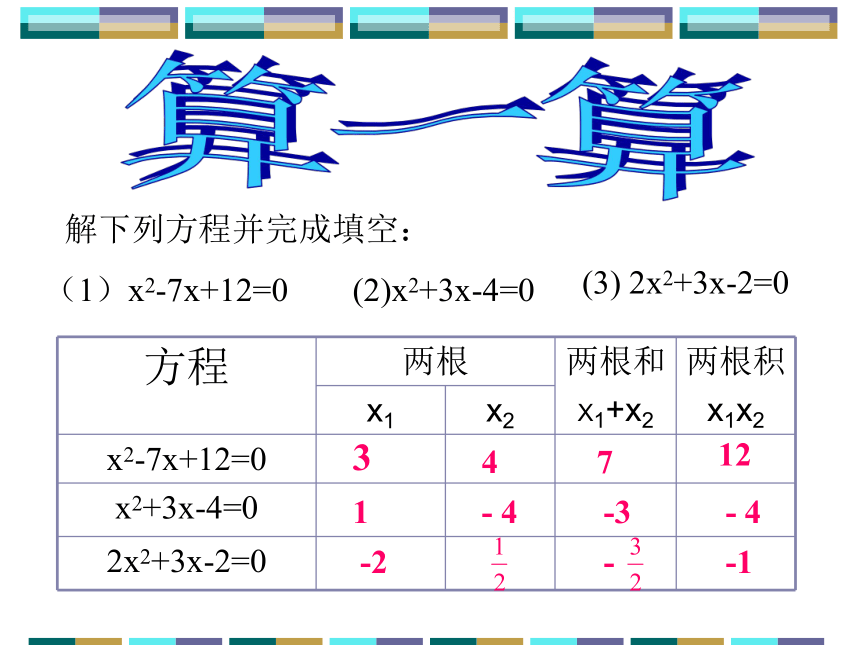
(1)x2-7x+12=0
(2)x2+3x-4=0
(3) 2x2+3x-2=0
解下列方程并完成填空:
方程 两根 两根和
X1+x2 两根积
x1x2
x1 x2
x2-7x+12=0
x2+3x-4=0
2x2+3x-2=0
3
4
12
7
1
-3
- 4
- 4
-1
-
-2
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
那么X1+x2= , X1x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
韦达(1540-1603)
韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
如果方程x2+px+q=0的两根是
X1 ,X2,那么X1+X2= ,
X1X2=
-P
q
说出下列各方程的两根之和与两根之积:
1、 x2 - 2x - 1=0
2、 2x2 - 3x + =0
3、 2x2 - 6x =0
4、 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
例1、已知3x2+2x-9=0的两根是x1 , x2 。
求:
(1) (2) x12+x22
解:
由题意可知x1+x2= - , x1 · x2=-3
(1)
=
=
=
(2)∵ (x1+x2)2= x12+x22 +2x1x2
∴x12+x22 =(x1+x2)2 -2x1x2
=(- )2
-2×(-3)=6
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解:
设方程的另一个根为x1.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由根与系数关系,得x1●2=3k
即 2 x1 =-6
∴ x1 =-3
答:方程的另一个根是-3 , k的值是-2。
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解二:
设方程的另一个根为x1.
由根与系数的关系,得
x1 +2= k+1
x1 ●2= 3k
解这方程组,得
x1 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2。
已知x1,x2是方程3x2+px+q=0的两个根,
分别根据下列条件求出p和q的值:
(1) x1 = 1, x2 =2
(2) x1 = 3, x2 = -6
(3) x1 = - , x2 =
(4) x1 = -2+ , x2 = -2-
由根与系数的关系,得
解:
x1+x2= - , x1 · x2=
∴p= -3(x1+x2) q=3 x1 · x2
(1)p= -9 q= 6
(2)p= 9 q= -54
(3)p= 0 q= -21
(4)p= 12 q= -3
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
解:设方程的另一个根为x1,
则x1+1= ,
∴ x1= ,
又x1●1= ,
∴ m= 3x1 = 16
解:
由根与系数的关系,得
x1+x2= - 2 , x1 · x2=
∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=
1、一元二次方程根与系数关系及其推论
2、利用此关系解决有关一元二次方程
根与系数问题时,注意两个隐含条件:
(1)二次项系数a≠0
(2)根的判别式b2-4ac≥0
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2= , x1x2=
∴
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2
∴ X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22 =4,得2k2-8k+4=4
解得k1=0 , k2=4
经检验, k2=4不合题意,舍去。
∴ k=0
一元二次方程根与系数的关系
一元二次方程 ax2+bx+c=0(a≠0) 的求根公式:
X=
(b2-4ac≥ 0)
(1)x2-7x+12=0
(2)x2+3x-4=0
(3) 2x2+3x-2=0
解下列方程并完成填空:
方程 两根 两根和
X1+x2 两根积
x1x2
x1 x2
x2-7x+12=0
x2+3x-4=0
2x2+3x-2=0
3
4
12
7
1
-3
- 4
- 4
-1
-
-2
一元二次方程的根与系数的关系:
如果方程ax2+bx+c=0(a≠0)的两个根是X1 , X2 ,
那么X1+x2= , X1x2=
-
(韦达定理)
注:能用根与系数的关系的前提条件为b2-4ac≥0
韦达(1540-1603)
韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号,并对方程论做了改进。 他生于法国的普瓦图。年青时学习法律当过律师,后从事政治活动,当过议会的议员,在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究,第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。 韦达在欧洲被尊称为“代数学之父”。
一元二次方程根与系数关系的证明:
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
如果方程x2+px+q=0的两根是
X1 ,X2,那么X1+X2= ,
X1X2=
-P
q
说出下列各方程的两根之和与两根之积:
1、 x2 - 2x - 1=0
2、 2x2 - 3x + =0
3、 2x2 - 6x =0
4、 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
例1、已知3x2+2x-9=0的两根是x1 , x2 。
求:
(1) (2) x12+x22
解:
由题意可知x1+x2= - , x1 · x2=-3
(1)
=
=
=
(2)∵ (x1+x2)2= x12+x22 +2x1x2
∴x12+x22 =(x1+x2)2 -2x1x2
=(- )2
-2×(-3)=6
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解:
设方程的另一个根为x1.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由根与系数关系,得x1●2=3k
即 2 x1 =-6
∴ x1 =-3
答:方程的另一个根是-3 , k的值是-2。
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解二:
设方程的另一个根为x1.
由根与系数的关系,得
x1 +2= k+1
x1 ●2= 3k
解这方程组,得
x1 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2。
已知x1,x2是方程3x2+px+q=0的两个根,
分别根据下列条件求出p和q的值:
(1) x1 = 1, x2 =2
(2) x1 = 3, x2 = -6
(3) x1 = - , x2 =
(4) x1 = -2+ , x2 = -2-
由根与系数的关系,得
解:
x1+x2= - , x1 · x2=
∴p= -3(x1+x2) q=3 x1 · x2
(1)p= -9 q= 6
(2)p= 9 q= -54
(3)p= 0 q= -21
(4)p= 12 q= -3
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
解:设方程的另一个根为x1,
则x1+1= ,
∴ x1= ,
又x1●1= ,
∴ m= 3x1 = 16
解:
由根与系数的关系,得
x1+x2= - 2 , x1 · x2=
∴ (x1+1)(x2+1) = x1 x2 + (x1+x2)+1 =-2+( )+1=
1、一元二次方程根与系数关系及其推论
2、利用此关系解决有关一元二次方程
根与系数问题时,注意两个隐含条件:
(1)二次项系数a≠0
(2)根的判别式b2-4ac≥0
1、当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵ (x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2= , x1x2=
∴
解得k1=9,k2= -3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2= 2(k-1) , x1x2=k2
∴ X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22 =4,得2k2-8k+4=4
解得k1=0 , k2=4
经检验, k2=4不合题意,舍去。
∴ k=0
