安徽省阜阳市九校联盟2022-2023学年九年级下学期数学 第一次月考试卷(含解析)
文档属性
| 名称 | 安徽省阜阳市九校联盟2022-2023学年九年级下学期数学 第一次月考试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 954.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 21:25:52 | ||
图片预览




文档简介
阜阳市2023年九年级数学九校联盟第一次月考试卷
一、单选题(共10题;共40分)
1.(4分)2的相反数是( )
A.2 B. C. D.1
2.(4分)中国互联网络信息中心发布的《第34次中国互联网络发展状况统计报告》显示,截止到2023年7月,中国手机网民数量比2013年底增加26990000人,其中数据26990000用科学记数法表示为( )
A. B. C. D.
3.(4分)如图是某几何体的三视图,则该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
4.(4分)下列计算正确的是( )
A. B.
C. D.
5.(4分)如图是一副三角板,其中,,,若点B与点F重合,点D在AB边上,AC与EF交于点G,则的度数为( )
A.45° B.60° C.65° D.75°
6.(4分)不透明袋子中装有10个球,其中有6个红球和4个白球,它们除颜色外其余都相同.从袋子中随机摸出1个球,是红球的概率为( )
A. B. C. D.
7.(4分)在平面直角坐标系中,若将一次函数的图象向下平移2个单位长度后经过点,则b的值为( )
A.4 B. C.0 D.2
8.(4分)如图,的弦,且于点E,连接.若,则的半径为( )
A. B. C. D.3
9.(4分)如图,点A、C为反比例函数图象上的点,过点A、C分别作轴,轴,垂足分别为B、D,连接、、,线段交于点E,点E恰好为的中点,当的面积为6时,k的值为( )
A. B.8 C. D.
10.(4分)如图,在中,,,,动点M,N分别在边,上则的最小值是( )
A. B. C.6 D.
二、填空题(共4题;共20分)
11.(5分)当 时,分式 的值为零.
12.(5分)因式分解的结果是 .
13.(5分)如图,在等腰中,,,D为边的中点,过点C作于点E,交于点F,则线段的长为 .
14.(5分)关于抛物线,与x轴交于A、B两点(A在B左侧),给出下列4个结论:①当抛物线的顶点在y轴的正半轴上时,;②点P在抛物线上,当符合条件(a为常数)的点有3个时,则;③当 时,y<0,;④已知C(0,2),D(0,4),当取最小值时,.其中正确结论的序号是 .
三、计算题(共1题;共8分)
15.(8分)先化简,再求值:,其中,.
四、作图题(共1题;共8分)
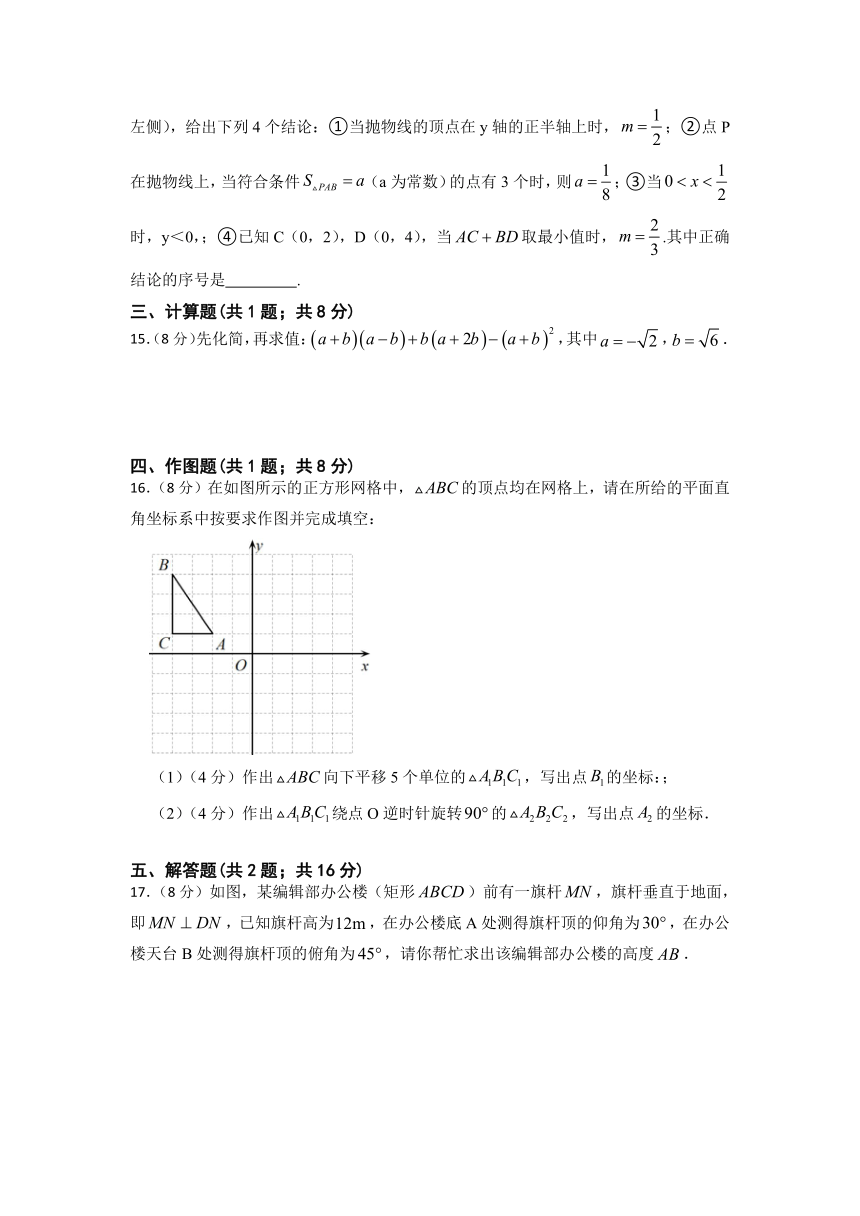
16.(8分)在如图所示的正方形网格中,的顶点均在网格上,请在所给的平面直角坐标系中按要求作图并完成填空:
(1)(4分)作出向下平移5个单位的,写出点的坐标:;
(2)(4分)作出绕点O逆时针旋转的,写出点的坐标.
五、解答题(共2题;共16分)
17.(8分)如图,某编辑部办公楼(矩形)前有一旗杆,旗杆垂直于地面,即,已知旗杆高为,在办公楼底A处测得旗杆顶的仰角为,在办公楼天台B处测得旗杆顶的俯角为,请你帮忙求出该编辑部办公楼的高度.
18.(8分)习近平总书记来到陕西省柞水县小岭镇金米村实地考察,得知木耳喜获丰收.小木耳作出大产业,2019年王极东木耳一项净收入4万元,2021年净收入达到5.76万元,则两年的平均增长率是多少?
六、综合题(共5题;共58分)
19.(10分)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:
第4个等式:,
……
请根据以上规律,解决下列问题
(1)(5分)试写出第5个等式;
(2)(5分)请证明第4个等式.
20.(10分)如图,直线l与相离,于点A,与相交于点P,.C是直线l上一点,连接并延长,交于点B,且.
(1)(5分)求证:是的切线;
(2)(5分)若,求线段的长.
21.(12分)“读书让生活更加多彩,阅读让城市更有温度”.近年来,作为深圳中心城区和“首善之区”的福田各学校积极打造“阅读永恒、书香满溢”的爱阅之校.为了解今年福田区15000名初三学生的每天平均课外阅读时间,从中随机抽取若干名学生进行问卷调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 时间(小时) 频数(人数) 频率
A 0≤t<0.5 40 0.1
B 0.5≤t<1 a 0.3
C 1≤t<1.5 140 b
D 1.5≤t<2 80 0.2
E 2≤t<2.5 20 0.05
(1)(1分)表中的a= ,b= ;
(2)(5分)补全频数分布直方图;
(3)(5分)结合调查信息,请你估计今年该区初三学生中,每天课外阅读小于1小时的学生约有多少人?
22.(12分)为鼓励大学毕业生自主创业,某市政府出台相关政策,本市企业提供产品给大学毕业生自主销售,政府还给予大学毕业生一定补贴.已知某种品牌服装的成本价为每件100元,每件政府补贴20元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣3x+900.
(1)(4分)若第一个月将销售单价定为160元,政府这个月补贴多少元?
(2)(4分)设获得的销售利润(不含政府补贴)为w(元),当销售单价为多少元时,每月可获得最大销售利润
(3)(4分)若每月获得的总收益(每月总收益=每月销售利润+每月政府补贴)不低于28800
元,求该月销售单价的最小值.
23.(14分)在中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)(4分)求证:;
(2)(4分)证明:四边形ADCF是菱形:
(3)(6分)若AC=3,AB=4,求菱形ADCF的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:2的相反数是,
故答案为:B.
【分析】根据只有符号不同的两个数互为相反数解答即可.
2.【答案】C
【解析】【解答】解:,
故答案为:C.
【分析】 把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。根据科学记数法的定义计算求解即可。
3.【答案】C
【解析】【解答】解:∵几何体的主视图和俯视图都是宽度相等的长方形,
∴该几何体是一个柱体,
∵俯视图是一个圆,
∴该几何体是一个圆柱体;
故答案为:C.
【分析】利用三视图的定义求解即可。
4.【答案】D
【解析】【解答】解:A、2a与3b不是同类项,不能合并,故此选项不符合题意;
B、,故此选项不符合题意;
C、与不是同类项,不能合并,故此选项不符合题意;
D、,故此选项符合题意.
故答案为:D.
【分析】整式加法的实质就是合并同类项,所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序没有关系,与系数也没有关系,合并同类项的时候,只需要将系数相加减,字母和字母的指数不变,但不是同类项的一定就不能合并,从而即可一一判断,得出答案.
5.【答案】D
【解析】【解答】解:由题意可知:,,,
所以可知:∠DBE=60°,
∠EBC=90°-60°=30°,
所以∠EGC=∠EBC+∠C=45°+30°=75°,
故答案为:D.
【分析】先求出∠EBC=90°-60°=30°,再利用三角形外角的性质可得∠EGC=∠EBC+∠C=45°+30°=75°。
6.【答案】C
【解析】【解答】解:不透明袋子中装有10个球,其中有6个红球和4个白球,
从袋子中随机摸出1个球,是红球的概率为:,
故答案为:C.
【分析】用袋中红色小球的数量除以袋中小球的总数量,计算即可.
7.【答案】A
【解析】【解答】解:将一次函数的图象向下平移2个单位得到,
把点代入得,,
解得b=4.
故答案为:A
【分析】先求出平移后的解析式为,再将点代入解析式求出b的值即可。
8.【答案】C
【解析】【解答】解:连接、、,
∵的弦,
,
,
,
,
,
,
,
是等腰直角三角形,
在中,,
,,
,
,
故答案为:C.
【分析】连接AB、AO、OD,由弦、弧以及圆周角定理可得∠BAC=∠ABD,∠AOD=2∠ABD=90°,推出△AOD是等腰直角三角形,然后利用勾股定理进行计算.
9.【答案】A
【解析】【解答】解:设点C的坐标为,则点,,,,
,
.
故答案为:A.
【分析】设C(m,),则E(m,),A(m,),根据三角形的面积公式可得S△AEC=BD·AE=k=6,求解可得k的值.
10.【答案】D
【解析】【解答】解:如图,作点C关于直线的对称点P,过点P作于点N,交于点M,连接,此时最小.
在中,∵,,,
∴,
∴.
又∵,
∴,解得.
由对称得,.
∵,
∴.
∵,
∴,
∴,
∴,即的最小值为
故答案为:D
【分析】作点C关于直线的对称点P,过点P作于点N,交于点M,连接,此时最小,再求出PN的长即可。
11.【答案】0
【解析】【解答】解:由题意,得2x=0,且x+2≠0,解得:x=0,
故答案为:0.
【分析】根据分式的值为零的条件:分母不为0,且分子为0,据此可得2x=0,且x+2≠0,求解可得x的值.
12.【答案】(y+2x)(y-2x)
【解析】【解答】解:.
故答案为:(y+2x)(y-2x).
【分析】利用平方差公式进行因式分解即可。
13.【答案】
【解析】【解答】解:过B作交延长线于G,
,
,
,
,
,,
,
,
是的中点,
,
,,
,
,
,
,
是等腰直角三角形,
,
.
故答案为:.
【分析】过B作BG⊥BC交CF的延长线于G,根据同角的余角相等可得∠CAD=∠BCG,利用ASA证明△CBG≌△ACD,得到BG=CD,结合中点的概念可得BG=CD=BC=1,根据垂直于同一直线的两直线互相平行可得AC∥BG,由平行于三角形一边的直线和其他两边或两边的延长线相交,所构成的三角形与原三角形相似可得△BGF∽△ACF,由相似三角形的性质可得BF=AB,由等腰直角三角形的性质可得AB=BC=,据此计算.
14.【答案】②④
【解析】【解答】解:① 抛物线的顶点在y轴的正半轴上,要,且,
∵m无解,故①错误;
②∵
,
∴顶点的纵坐标为,
当时,,
解得,,
∴,,
则,
∵抛物线上有一个动点P,满足的点有3个时,
∴点P是抛物线的顶点时满足条件,
此时,故②正确;
③∵,,,,
∴由数形结合可知: ,
解得:,故③错误;
④如图,作点C关于点O的对称点E,由②,将AB平移到EF,连接DF交x轴于G,
∵,
显然当D,B,F共线时,
即点B运动到点G时,取得最小值,
∵,
∴,
∴,
∵,这时点B和点G重合,
∴,故④正确;
综上所述,正确结论的序号是②④,
故答案为:②④.
【分析】①由抛物线的顶点在y轴的正半轴上,则,且,据此得解接口判断;②将解析式化为 ,可得顶点的纵坐标为,再求出,,从而得出AB=1,结合已知可得得点P是抛物线的顶点时满足条件,利用三角形的面积公式求出a值即可判断;③由,及A、B的坐标,可得,据此求解即可判断;④作点C关于点O的对称点E,由②,将AB平移到EF,连接DF交x轴于G,由于,显然当D,B,F共线时,即点B运动到点G时,取得最小值,根据平行线分线段成比例可求出OG的长,即得B的坐标,从而求出m值即可判断.
15.【答案】解:原式;
∵,,
∴.
【解析】【分析】先利用整式的混合运算化简,再将a、b的值代入计算即可。
16.【答案】(1)解:如图,即为所求,点的坐标为,
故答案为:;
(2)解:如图,即为所求,点的坐标为,
故答案为:.
【解析】【分析】(1)分别作出A、B、C的对应点A1、B1、C1,顺次连接,写出点的坐标;
(2)分别作出A、B、C的对应点A2、B2、C2,顺次连接,写出点A2的坐标。
17.【答案】解:如图,过点M作于点H,
∵,
∴四边形是矩形,
∴,,
∴,
在中,,
∵在办公楼天台B处测得旗杆顶的俯角为,且,
∴,
∴是等腰直角三角形,
∴,
∴,
答:办公楼的高度为.
【解析】【分析】先求出 , 再求出 , 最后计算求解即可。
18.【答案】解:设两年的平均增长率是x,由题意可知:
4(1+x)2=5.76
x1=0.2=20% x2=-2.2(舍去)
经检验x=0.2=20%符合题意.
答:两年的平均增长率为20%.
【解析】【分析】此题的等量关系为:2019年王极东木耳一项净收入×(1+增长率)2=2021年的净收入,设未知数,列方程求解即可.
19.【答案】(1)解:由题意可知:
(2)证明:方法一:设,
∴,
又∵,
∴,
∴,
∴,即;
方法二:,
.
∴原等式成立;
方法三 :右边,
左边,
∵左边=右边,
∴原等式成立.
【解析】【分析】(1)根据题意求出即可作答;
(2)根据题意找出规律,计算求解即可。
20.【答案】(1)证明:连接,则,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴是的切线;
(2)解:如图,过点O作于D,
∵,
∴设,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,,
∴.
【解析】【分析】(1)连接OB,则OP=OB,由等腰三角形的性质以及对顶角的性质可得∠OBP=∠OPB=∠CPA,∠ACB=∠ABC,结合∠ACB+∠CPA=90°可得∠ABO=90°,据此证明;
(2)过点O作OD⊥BP于D,根据三角函数的概念可设AP=x,则AC=2x,OP=OB=5-x,利用勾股定理可得x的值,然后求出AP、AC、OP、CP的值,根据两角对应相等的两个三角形相似可得△ACP∽△DOP,由相似三角形的性质可得PD的值,根据等腰三角形的性质可得BP=2PD,据此计算.
21.【答案】(1)120;0.35
(2)解:补全频数分布直方图如下图:
(3)解:15000×(0.1+0.3)=6000人答:估计今年该区初三学生中,每天课外阅读小于1小时的学生约有6000人
【解析】【解答】解:(1)∵被抽取的学生总人数为20÷0.05=400(名),
∴a=400×0.3=120.b=140÷400=0.35,故答案为:120;0.35
【分析】(1)先求得抽取的学生数,再根据频率计算频数,根据频数计算频率;
(2)根据每周课余阅读时间不足0.5小时的学生的频率,估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生数即可;
(3)通过画树状图,根据概率的计算公式,即可得到抽取的两名学生刚好是1名男生和1名女生的概率
22.【答案】(1)解:当x=160时,y=-3x+900=-3×160+900=420,
∴补贴为420×20=8400元;
(2)解:设销售单价为x元,
w=(-3x+900)(x-100)=-3(x-200)2+30000
∴当x=200时,当月销售利润最大;
(3)解:设当月总收益为p元,
∴p=(-3x+900)(x-100)+20(-3x+900)=(-3x+900)(x-80)=-3(x-190)2+36300,
当-3(x-190)2+36300=28800时,
∴x1=240,x2=140,
∵二次函数抛物线开口向下,p≥28800,
∴140≤x≤240,
∴销售单价的最小值为140元.
【解析】【分析】(1)将x=160代入y=-3x+900可算出本月的销售数量,进而根据每件政府补贴20元即可求解;
(2)设销售单价为x元,则每件利润为(x-100)元,进而根据单件服装的利润×当月的销售数量=总利润建立出函数关系式,进而根据所得函数的性质即可解决问题;
(3)设当月总收益为p元,根据每月总收益=每月销售利润+每月政府补贴建立出函数关系式,进而将p=28800代入所得函数解析式,求解得出对应的x的值,即售价,从而结合函数图象的开口方向得到自变量x的取值范围,此题得解.
23.【答案】(1)证明:∵,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
∴;
(2)证明:由(1)知,,
则AF=DB,
∵DB=DC,
∴AF=CD,
∵,
∴四边形ADCF是平行四边形
∵∠BAC=90°,D是BC的中点,
∴,
∴四边形ADCF是菱形;
(3)解:连接DF,如图所示:
∵,,
∴四边形ABDF是平行四边形,
∴DF=AB=4,
∵四边形ADCF是菱形,
∴菱形ADCF的面积.
【解析】【分析】(1)根据AAS证明△AEF≌△DEB;
(2)由(1)△AEF≌△DEB,可得AF=DB,结合线段的中点可得AF=CD=BD,由AF∥BC可证四边形ADCF是平行四边形,利用直角三角形斜边中线的性质可得AD=CD,根据菱形的判定即证;
(3)连接DF,先证四边形ABDF是平行四边形, 可得DF=AB=4, 根据菱形ADCF的面积即可求解.
一、单选题(共10题;共40分)
1.(4分)2的相反数是( )
A.2 B. C. D.1
2.(4分)中国互联网络信息中心发布的《第34次中国互联网络发展状况统计报告》显示,截止到2023年7月,中国手机网民数量比2013年底增加26990000人,其中数据26990000用科学记数法表示为( )
A. B. C. D.
3.(4分)如图是某几何体的三视图,则该几何体是( )
A.正方体 B.圆锥 C.圆柱 D.球
4.(4分)下列计算正确的是( )
A. B.
C. D.
5.(4分)如图是一副三角板,其中,,,若点B与点F重合,点D在AB边上,AC与EF交于点G,则的度数为( )
A.45° B.60° C.65° D.75°
6.(4分)不透明袋子中装有10个球,其中有6个红球和4个白球,它们除颜色外其余都相同.从袋子中随机摸出1个球,是红球的概率为( )
A. B. C. D.
7.(4分)在平面直角坐标系中,若将一次函数的图象向下平移2个单位长度后经过点,则b的值为( )
A.4 B. C.0 D.2
8.(4分)如图,的弦,且于点E,连接.若,则的半径为( )
A. B. C. D.3
9.(4分)如图,点A、C为反比例函数图象上的点,过点A、C分别作轴,轴,垂足分别为B、D,连接、、,线段交于点E,点E恰好为的中点,当的面积为6时,k的值为( )
A. B.8 C. D.
10.(4分)如图,在中,,,,动点M,N分别在边,上则的最小值是( )
A. B. C.6 D.
二、填空题(共4题;共20分)
11.(5分)当 时,分式 的值为零.
12.(5分)因式分解的结果是 .
13.(5分)如图,在等腰中,,,D为边的中点,过点C作于点E,交于点F,则线段的长为 .
14.(5分)关于抛物线,与x轴交于A、B两点(A在B左侧),给出下列4个结论:①当抛物线的顶点在y轴的正半轴上时,;②点P在抛物线上,当符合条件(a为常数)的点有3个时,则;③当 时,y<0,;④已知C(0,2),D(0,4),当取最小值时,.其中正确结论的序号是 .
三、计算题(共1题;共8分)
15.(8分)先化简,再求值:,其中,.
四、作图题(共1题;共8分)
16.(8分)在如图所示的正方形网格中,的顶点均在网格上,请在所给的平面直角坐标系中按要求作图并完成填空:
(1)(4分)作出向下平移5个单位的,写出点的坐标:;
(2)(4分)作出绕点O逆时针旋转的,写出点的坐标.
五、解答题(共2题;共16分)
17.(8分)如图,某编辑部办公楼(矩形)前有一旗杆,旗杆垂直于地面,即,已知旗杆高为,在办公楼底A处测得旗杆顶的仰角为,在办公楼天台B处测得旗杆顶的俯角为,请你帮忙求出该编辑部办公楼的高度.
18.(8分)习近平总书记来到陕西省柞水县小岭镇金米村实地考察,得知木耳喜获丰收.小木耳作出大产业,2019年王极东木耳一项净收入4万元,2021年净收入达到5.76万元,则两年的平均增长率是多少?
六、综合题(共5题;共58分)
19.(10分)观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:
第4个等式:,
……
请根据以上规律,解决下列问题
(1)(5分)试写出第5个等式;
(2)(5分)请证明第4个等式.
20.(10分)如图,直线l与相离,于点A,与相交于点P,.C是直线l上一点,连接并延长,交于点B,且.
(1)(5分)求证:是的切线;
(2)(5分)若,求线段的长.
21.(12分)“读书让生活更加多彩,阅读让城市更有温度”.近年来,作为深圳中心城区和“首善之区”的福田各学校积极打造“阅读永恒、书香满溢”的爱阅之校.为了解今年福田区15000名初三学生的每天平均课外阅读时间,从中随机抽取若干名学生进行问卷调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
组别 时间(小时) 频数(人数) 频率
A 0≤t<0.5 40 0.1
B 0.5≤t<1 a 0.3
C 1≤t<1.5 140 b
D 1.5≤t<2 80 0.2
E 2≤t<2.5 20 0.05
(1)(1分)表中的a= ,b= ;
(2)(5分)补全频数分布直方图;
(3)(5分)结合调查信息,请你估计今年该区初三学生中,每天课外阅读小于1小时的学生约有多少人?
22.(12分)为鼓励大学毕业生自主创业,某市政府出台相关政策,本市企业提供产品给大学毕业生自主销售,政府还给予大学毕业生一定补贴.已知某种品牌服装的成本价为每件100元,每件政府补贴20元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣3x+900.
(1)(4分)若第一个月将销售单价定为160元,政府这个月补贴多少元?
(2)(4分)设获得的销售利润(不含政府补贴)为w(元),当销售单价为多少元时,每月可获得最大销售利润
(3)(4分)若每月获得的总收益(每月总收益=每月销售利润+每月政府补贴)不低于28800
元,求该月销售单价的最小值.
23.(14分)在中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作交BE的延长线于点F.
(1)(4分)求证:;
(2)(4分)证明:四边形ADCF是菱形:
(3)(6分)若AC=3,AB=4,求菱形ADCF的面积.
答案解析部分
1.【答案】B
【解析】【解答】解:2的相反数是,
故答案为:B.
【分析】根据只有符号不同的两个数互为相反数解答即可.
2.【答案】C
【解析】【解答】解:,
故答案为:C.
【分析】 把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。根据科学记数法的定义计算求解即可。
3.【答案】C
【解析】【解答】解:∵几何体的主视图和俯视图都是宽度相等的长方形,
∴该几何体是一个柱体,
∵俯视图是一个圆,
∴该几何体是一个圆柱体;
故答案为:C.
【分析】利用三视图的定义求解即可。
4.【答案】D
【解析】【解答】解:A、2a与3b不是同类项,不能合并,故此选项不符合题意;
B、,故此选项不符合题意;
C、与不是同类项,不能合并,故此选项不符合题意;
D、,故此选项符合题意.
故答案为:D.
【分析】整式加法的实质就是合并同类项,所谓同类项就是所含字母相同,而且相同字母的指数也分别相同的项,同类项与字母的顺序没有关系,与系数也没有关系,合并同类项的时候,只需要将系数相加减,字母和字母的指数不变,但不是同类项的一定就不能合并,从而即可一一判断,得出答案.
5.【答案】D
【解析】【解答】解:由题意可知:,,,
所以可知:∠DBE=60°,
∠EBC=90°-60°=30°,
所以∠EGC=∠EBC+∠C=45°+30°=75°,
故答案为:D.
【分析】先求出∠EBC=90°-60°=30°,再利用三角形外角的性质可得∠EGC=∠EBC+∠C=45°+30°=75°。
6.【答案】C
【解析】【解答】解:不透明袋子中装有10个球,其中有6个红球和4个白球,
从袋子中随机摸出1个球,是红球的概率为:,
故答案为:C.
【分析】用袋中红色小球的数量除以袋中小球的总数量,计算即可.
7.【答案】A
【解析】【解答】解:将一次函数的图象向下平移2个单位得到,
把点代入得,,
解得b=4.
故答案为:A
【分析】先求出平移后的解析式为,再将点代入解析式求出b的值即可。
8.【答案】C
【解析】【解答】解:连接、、,
∵的弦,
,
,
,
,
,
,
,
是等腰直角三角形,
在中,,
,,
,
,
故答案为:C.
【分析】连接AB、AO、OD,由弦、弧以及圆周角定理可得∠BAC=∠ABD,∠AOD=2∠ABD=90°,推出△AOD是等腰直角三角形,然后利用勾股定理进行计算.
9.【答案】A
【解析】【解答】解:设点C的坐标为,则点,,,,
,
.
故答案为:A.
【分析】设C(m,),则E(m,),A(m,),根据三角形的面积公式可得S△AEC=BD·AE=k=6,求解可得k的值.
10.【答案】D
【解析】【解答】解:如图,作点C关于直线的对称点P,过点P作于点N,交于点M,连接,此时最小.
在中,∵,,,
∴,
∴.
又∵,
∴,解得.
由对称得,.
∵,
∴.
∵,
∴,
∴,
∴,即的最小值为
故答案为:D
【分析】作点C关于直线的对称点P,过点P作于点N,交于点M,连接,此时最小,再求出PN的长即可。
11.【答案】0
【解析】【解答】解:由题意,得2x=0,且x+2≠0,解得:x=0,
故答案为:0.
【分析】根据分式的值为零的条件:分母不为0,且分子为0,据此可得2x=0,且x+2≠0,求解可得x的值.
12.【答案】(y+2x)(y-2x)
【解析】【解答】解:.
故答案为:(y+2x)(y-2x).
【分析】利用平方差公式进行因式分解即可。
13.【答案】
【解析】【解答】解:过B作交延长线于G,
,
,
,
,
,,
,
,
是的中点,
,
,,
,
,
,
,
是等腰直角三角形,
,
.
故答案为:.
【分析】过B作BG⊥BC交CF的延长线于G,根据同角的余角相等可得∠CAD=∠BCG,利用ASA证明△CBG≌△ACD,得到BG=CD,结合中点的概念可得BG=CD=BC=1,根据垂直于同一直线的两直线互相平行可得AC∥BG,由平行于三角形一边的直线和其他两边或两边的延长线相交,所构成的三角形与原三角形相似可得△BGF∽△ACF,由相似三角形的性质可得BF=AB,由等腰直角三角形的性质可得AB=BC=,据此计算.
14.【答案】②④
【解析】【解答】解:① 抛物线的顶点在y轴的正半轴上,要,且,
∵m无解,故①错误;
②∵
,
∴顶点的纵坐标为,
当时,,
解得,,
∴,,
则,
∵抛物线上有一个动点P,满足的点有3个时,
∴点P是抛物线的顶点时满足条件,
此时,故②正确;
③∵,,,,
∴由数形结合可知: ,
解得:,故③错误;
④如图,作点C关于点O的对称点E,由②,将AB平移到EF,连接DF交x轴于G,
∵,
显然当D,B,F共线时,
即点B运动到点G时,取得最小值,
∵,
∴,
∴,
∵,这时点B和点G重合,
∴,故④正确;
综上所述,正确结论的序号是②④,
故答案为:②④.
【分析】①由抛物线的顶点在y轴的正半轴上,则,且,据此得解接口判断;②将解析式化为 ,可得顶点的纵坐标为,再求出,,从而得出AB=1,结合已知可得得点P是抛物线的顶点时满足条件,利用三角形的面积公式求出a值即可判断;③由,及A、B的坐标,可得,据此求解即可判断;④作点C关于点O的对称点E,由②,将AB平移到EF,连接DF交x轴于G,由于,显然当D,B,F共线时,即点B运动到点G时,取得最小值,根据平行线分线段成比例可求出OG的长,即得B的坐标,从而求出m值即可判断.
15.【答案】解:原式;
∵,,
∴.
【解析】【分析】先利用整式的混合运算化简,再将a、b的值代入计算即可。
16.【答案】(1)解:如图,即为所求,点的坐标为,
故答案为:;
(2)解:如图,即为所求,点的坐标为,
故答案为:.
【解析】【分析】(1)分别作出A、B、C的对应点A1、B1、C1,顺次连接,写出点的坐标;
(2)分别作出A、B、C的对应点A2、B2、C2,顺次连接,写出点A2的坐标。
17.【答案】解:如图,过点M作于点H,
∵,
∴四边形是矩形,
∴,,
∴,
在中,,
∵在办公楼天台B处测得旗杆顶的俯角为,且,
∴,
∴是等腰直角三角形,
∴,
∴,
答:办公楼的高度为.
【解析】【分析】先求出 , 再求出 , 最后计算求解即可。
18.【答案】解:设两年的平均增长率是x,由题意可知:
4(1+x)2=5.76
x1=0.2=20% x2=-2.2(舍去)
经检验x=0.2=20%符合题意.
答:两年的平均增长率为20%.
【解析】【分析】此题的等量关系为:2019年王极东木耳一项净收入×(1+增长率)2=2021年的净收入,设未知数,列方程求解即可.
19.【答案】(1)解:由题意可知:
(2)证明:方法一:设,
∴,
又∵,
∴,
∴,
∴,即;
方法二:,
.
∴原等式成立;
方法三 :右边,
左边,
∵左边=右边,
∴原等式成立.
【解析】【分析】(1)根据题意求出即可作答;
(2)根据题意找出规律,计算求解即可。
20.【答案】(1)证明:连接,则,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴是的切线;
(2)解:如图,过点O作于D,
∵,
∴设,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,,
∴.
【解析】【分析】(1)连接OB,则OP=OB,由等腰三角形的性质以及对顶角的性质可得∠OBP=∠OPB=∠CPA,∠ACB=∠ABC,结合∠ACB+∠CPA=90°可得∠ABO=90°,据此证明;
(2)过点O作OD⊥BP于D,根据三角函数的概念可设AP=x,则AC=2x,OP=OB=5-x,利用勾股定理可得x的值,然后求出AP、AC、OP、CP的值,根据两角对应相等的两个三角形相似可得△ACP∽△DOP,由相似三角形的性质可得PD的值,根据等腰三角形的性质可得BP=2PD,据此计算.
21.【答案】(1)120;0.35
(2)解:补全频数分布直方图如下图:
(3)解:15000×(0.1+0.3)=6000人答:估计今年该区初三学生中,每天课外阅读小于1小时的学生约有6000人
【解析】【解答】解:(1)∵被抽取的学生总人数为20÷0.05=400(名),
∴a=400×0.3=120.b=140÷400=0.35,故答案为:120;0.35
【分析】(1)先求得抽取的学生数,再根据频率计算频数,根据频数计算频率;
(2)根据每周课余阅读时间不足0.5小时的学生的频率,估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生数即可;
(3)通过画树状图,根据概率的计算公式,即可得到抽取的两名学生刚好是1名男生和1名女生的概率
22.【答案】(1)解:当x=160时,y=-3x+900=-3×160+900=420,
∴补贴为420×20=8400元;
(2)解:设销售单价为x元,
w=(-3x+900)(x-100)=-3(x-200)2+30000
∴当x=200时,当月销售利润最大;
(3)解:设当月总收益为p元,
∴p=(-3x+900)(x-100)+20(-3x+900)=(-3x+900)(x-80)=-3(x-190)2+36300,
当-3(x-190)2+36300=28800时,
∴x1=240,x2=140,
∵二次函数抛物线开口向下,p≥28800,
∴140≤x≤240,
∴销售单价的最小值为140元.
【解析】【分析】(1)将x=160代入y=-3x+900可算出本月的销售数量,进而根据每件政府补贴20元即可求解;
(2)设销售单价为x元,则每件利润为(x-100)元,进而根据单件服装的利润×当月的销售数量=总利润建立出函数关系式,进而根据所得函数的性质即可解决问题;
(3)设当月总收益为p元,根据每月总收益=每月销售利润+每月政府补贴建立出函数关系式,进而将p=28800代入所得函数解析式,求解得出对应的x的值,即售价,从而结合函数图象的开口方向得到自变量x的取值范围,此题得解.
23.【答案】(1)证明:∵,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
∴;
(2)证明:由(1)知,,
则AF=DB,
∵DB=DC,
∴AF=CD,
∵,
∴四边形ADCF是平行四边形
∵∠BAC=90°,D是BC的中点,
∴,
∴四边形ADCF是菱形;
(3)解:连接DF,如图所示:
∵,,
∴四边形ABDF是平行四边形,
∴DF=AB=4,
∵四边形ADCF是菱形,
∴菱形ADCF的面积.
【解析】【分析】(1)根据AAS证明△AEF≌△DEB;
(2)由(1)△AEF≌△DEB,可得AF=DB,结合线段的中点可得AF=CD=BD,由AF∥BC可证四边形ADCF是平行四边形,利用直角三角形斜边中线的性质可得AD=CD,根据菱形的判定即证;
(3)连接DF,先证四边形ABDF是平行四边形, 可得DF=AB=4, 根据菱形ADCF的面积即可求解.
同课章节目录
