安徽省阜阳市十校联盟2022--2023学年下学期第三次月考数学试卷(含解析)
文档属性
| 名称 | 安徽省阜阳市十校联盟2022--2023学年下学期第三次月考数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 21:27:27 | ||
图片预览




文档简介
2023年阜阳市数学十校联盟第三次月考试卷
一、单选题(共10题;共40分)
1.(4分)相反数为5的数是( )
A.-5 B.5 C.±5 D.
2.(4分)截至2022年10月,我国基本医疗保险参保人数已超过13.6亿人,其中数据13.6亿用科学记数法表示为( )
A. B. C. D.
3.(4分)下面计算正确的是( )
A.2x2+2x2=4x4 B.(x﹣y)2=x2﹣y2
C.﹣x2 (﹣x)2=x4 D.(﹣2x2)3=﹣8x6
4.(4分)如图所示的石板凳,它的俯视图是( )
A. B.
C. D.
5.(4分)如图,在同一条道路上,甲车从地到地,乙车从地到地,甲车和乙车同时匀速出发,甲车先到达目的地,图中的折线段表示甲、乙两车之间的距离(单位:km)与行驶时间(单位:h)的函数关系图象,下列说法错误的是( ).
A.甲、乙两车相遇时间为 B.甲车速度为
C.乙车速度为 D.甲车比乙车早
6.(4分) 如图,平行四边形的对角线与相交于点,,垂足为,,,,则的长为( )
A. B. C. D.
7.(4分)若关于的一元二次方程的一个根为,则的值为( )
A.3 B.0 C.-3 D.-3或3
8.(4分)在一个桌子上放着若干张背面向上的扑克牌,这些扑克牌背面图案相同,正面为3张方块、2张红桃和张梅花.若从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为,则的值为( )
A.4 B.5 C.6 D.7
9.(4分)如图,点A、C为反比例函数图象上的点,过点A、C分别作轴,轴,垂足分别为B、D,连接、、,线段交于点E,点E恰好为的中点,当的面积为6时,k的值为( )
A. B.8 C. D.
10.(4分)如图,在边长为3的正方形中,点E在边上,且.是以E为直角顶点的等腰直角三角形,分别交于点M,N,过点F作的垂线交的延长线于点G.连接,则下列结论错误的是( )
A. B. C. D.
二、填空题(共4题;共20分)
11.(5分)不等式的解集为 .
12.(5分)分解因式: .
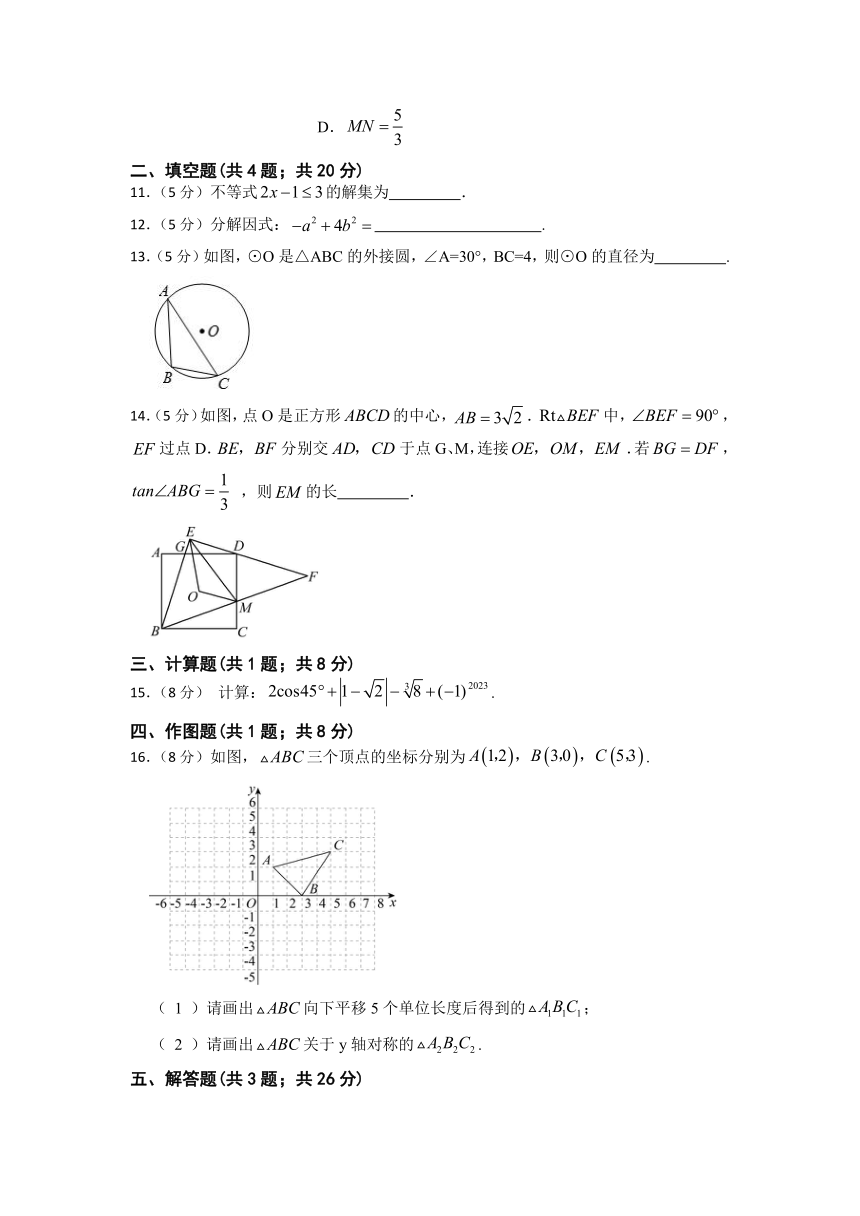
13.(5分)如图,⊙O是△ABC的外接圆,∠A=30°,BC=4,则⊙O的直径为 .
14.(5分)如图,点O是正方形的中心,.中,,过点D.分别交于点G、M,连接.若, ,则的长 .
三、计算题(共1题;共8分)
15.(8分) 计算:.
四、作图题(共1题;共8分)
16.(8分)如图,三个顶点的坐标分别为.
( 1 )请画出向下平移5个单位长度后得到的;
( 2 )请画出关于y轴对称的.
五、解答题(共3题;共26分)
17.(8分)先化简,再求值: ,其中 .
18.(8分)清朝数学家梅文鼎的《方程论》中有这样一题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,每亩场地折实田多少?
译文为:若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?
19.(10分)消防车是灭火救灾的主要装备.如图1是一辆登高云梯消防车的实物图,图2是其工作示意图.当云梯升起时,与底盘的夹角为α,液压杆与底盘的夹角为β.已知液压杆m,当,时,求的长.(结果精确到m,参考数据:,,)
六、综合题(共4题;共48分)
20.(10分)幸福成都,美在文明!为助力成都争全国文明典范城市,某校采用四种宣传形式:A.宣传单宣传,B.电子屏宣传,C.黑板报宣传,D.志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
请结合图中所给信息,解答下列问题:
(1)(3分)本次调查的学生共有 人,请补全条形统计图;
(2)(3分)扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为 ;
(3)(4分)本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率
21.(12分)如图,是的直径,是弦,是的中点,与交于点,是延长线上的一点,且.
(1)(6分)求证:为的切线;
(2)(6分)连接,取的中点,连接.若,,求的长.
22.(12分)如图,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,.
(1)(3分)求抛物线的函数表达式;
(2)(4分)如图1,连接BC,点P在抛物线上,且,求点P的坐标;
(3)(5分)如图2,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,,点M到x轴的距离为2L,的面积为5L,且,请问的长是否为定值?如果是,请直接写出这个定值;如果不是,请说明理由.
23.(14分)如图,四边形是矩形,点A、C分别在x轴、y轴上,是绕点O顺时针旋转得到的,点D在x轴上,直线交y轴于点F,交于点H,点B的坐标为.
(1)(4分)求直线的表达式;
(2)(4分)求的面积;
(3)(6分)点M在x轴上,平面内处否存在点N,使以点D、F、M、N为顶点的四边形是矩形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:相反数为-5.
故答案为:A.
【分析】只有符号不同的两个数叫做互为相反数,据此解答即可.
2.【答案】B
【解析】【解答】13.6亿,
故答案为:B.
【分析】 把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。根据科学记数法的定义计算求解即可。
3.【答案】D
【解析】【解答】解:A、2x2+2x2=4x2,原式计算错误,故答案为:不符合题意;
B、(x﹣y)2=x2﹣2xy+y2,原式计算错误,故答案为:不符合题意;
C、﹣x2 (﹣x)2=﹣x2 x2=﹣x4,原式计算错误,故答案为:不符合题意;
D、(﹣2x2)3=﹣8x6,原式计算正确,故答案为:符合题意.
故答案为:D.
【分析】根据合并同类项、完全平方公式、同底数幂的乘法、幂的乘方与积的乘方分别计算,再判断即可.
4.【答案】D
【解析】【解答】解:俯视图是从物体的上面看得到的平面图形,该几何体从上面看到的是 .
故答案为:D.
【分析】利用三视图的定义求解即可。
5.【答案】D
【解析】【解答】解:A.出发1小时后,两车相距为零,即两车相遇,故不符合题意;
B.甲车速度为,故不符合题意;
C.乙车速度为,故不符合题意;
D.甲车比乙车早,故符合题意;
故答案为:D.
【分析】根据所给的函数图象,结合题意,对每个选项一一判断即可。
6.【答案】D
【解析】【解答】解:四边形为平行四边形,,,
,,
,
,
为直角三角形,且,
,
,
,
解得.
故答案为:D.
【分析】根据平行四边形的性质可得OA=AC=1,OB=BD=,由勾股定理逆定理知△AOB为直角三角形,且∠BAO=90°,利用勾股定理可求出BC的值,然后根据等面积法进行计算.
7.【答案】C
【解析】【解答】解:关于的一元二次方程的一个根为0,
∴m2-9=0且m-3≠0
解之:m=±3,m≠3,
∴m=-3.
故答案为:C
【分析】利用一元二次方程的定义,可知m-3≠0,将x=0代入方程,可得到m2-9=0,分别求解,可求出m的值.
8.【答案】B
【解析】【解答】解:根据题意得:
,
解得:,
故答案为:B.
【分析】根据题意先求出 从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为, 列方程,再求解即可。
9.【答案】A
【解析】【解答】解:设点C的坐标为,则点,,,,
,
.
故答案为:A.
【分析】设C(m,),则E(m,),A(m,),根据三角形的面积公式可得S△AEC=BD·AE=k=6,求解可得k的值.
10.【答案】D
【解析】【解答】A、∵边长为3的正方形,
∴,
∴;
∵是以E为直角顶点的等腰直角三角形,
∴,不符合题意;
B、∵边长为3的正方形, ,
∴,
∵是以E为直角顶点的等腰直角三角形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,不符合题意;
C、过点F作于点H,
∵,
∴四边形是正方形,
∴,
∵,,
∴,,
∴,
∴,
∴,
∴,不符合题意;
D、∵,
∴,
∴,符合题意;
故答案为:D.
【分析】由AB=3,AE=2,利用勾股定理求出BE==EF,据此判断A;根据AAS证明△BAE≌△EGF,可得AB=EG=3,AE=GF=2,从而求出DG=EG-DE=2,利用勾股定理求出DF的长,即可判断B;过点F作于点H,证四边形DGFH为正方形,可得DH=2,CH=1,再证△HFN∽△CBN,△DEM∽△HFN,利用相似三角形的性质求出CN、HN、HM、MN,即可判断C、D。
11.【答案】x≤2
【解析】【解答】解:,
移项合并得:,
化系数为1得:x≤2,
故答案为:x≤2.
【分析】利用不等式的性质及不等式的解法求出解集即可。
12.【答案】(2b+a)(2b-a)
【解析】【解答】解:,
故答案为:(2b+a)(2b-a).
【分析】利用加法交换律把多项式整理成两个因式平方差的形式,进而利用平方差公式直接分解因式即可.
13.【答案】8
【解析】【解答】解:如图,连接OB,OC,
∵∠A=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
又∵BC=4,
∴BO=CO=BC=BC=4,
∴⊙O的直径为8,
故答案为:8.
【分析】连接OB,OC,依据△BOC是等边三角形,即可得到BO=CO=BC=BC=4,进而得出⊙O的直径为8.
14.【答案】
【解析】【解答】解:如图,过点F作于点H,
正方形ABCD,
,,
,
,
,,
,,
,
,
,
,
故答案为:.
【分析】利用正方形的性质求出,,再求出,最后利用全等三角形的判定与性质,勾股定理计算求解即可。
15.【答案】解:
【解析】【分析】根据特殊角三角函数值、绝对值、开立方、乘方先计算,再计算加减即可.
16.【答案】解:( 1 )如图,即为所求.
( 2 )如图,即为所求.
【解析】【分析】(1)分别将点A、B、C向下平移5个单位长度得到点A1、B1、C1的位置,然后顺次连接即可;
(2)关于y轴对称的点,横坐标互为相反数,纵坐标相同,据此找出点A2、B2、C2的位置,然后顺次连接即可.
17.【答案】解:原式=
=
= ,
当 , 时,
原式= .
【解析】【分析】根据单项式与多项式的乘法法则、完全平方公式、平方差公式分别去括号,再合并同类项对原式进行化简,然后将a、b的值代入进行计算.
18.【答案】解:设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩.
可列方程组为
解得
答:每亩山田相当于实田0.9亩,每亩场地相当于实田 亩.
【解析】【分析】 设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩,根据“若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩”列出方程组,求解即可.
19.【答案】解:在中,,m.
,
,
∴,∴m.
,
,m.
在中,
,
,
m.
∴m.
答:的长约为m.
【解析】【分析】结合题意,利用锐角三角函数计算求解即可。
20.【答案】(1)50
补全条形统计图如图所示:
(2)108°
(3)解:列表得:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中恰好是甲和乙的有2种,
∴被选取的两人恰好是甲和乙的概率是.
【解析】【解答】解:(1)本次调查的学生共有:(人),
喜欢B.电子屏宣传的人数有:(人),
补全条形统计图如图所示:
故答案为:50
(2)“D.志愿者宣传”对应的扇形圆心角度数为;
故答案为:;
【分析】(1)利用C的人数除以所占的比例可得总人数,然后求出B的人数,进而可补全条形统计图;
(2)利用D的人数除以总人数,然后乘以360°可得所占扇形圆心角的度数;
(3)画出表格,找出总情况数以及恰好是甲和乙的情况数,然后根据概率公式进行计算.
21.【答案】(1)证明:如图1,连接,.
∵,
∴.
∵,
∴.
∵∠OED=∠FEC,
∴∠OED=∠FCE.
∵AB是⊙O的直径,D是AB 的中点,
∴∠DOE=90°.
∴∠OED+∠ODC=90°.
∴∠FCE+∠OCD=90°,即∠OCF=90°.
∴OC⊥CF.
∴CF为⊙O的切线.
(2)解:如图2,连接BC,过G作GH⊥AB,垂足为H.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OBC+∠FAC=90°,
∵OC=OB,
∴∠OBC=∠OCB,
∵∠FCO=∠FCB+∠OCB=90°,
∴∠FCB=∠FAC,
∵∠F=∠F,
∴△FCB∽△FAC,
∴FCFA=BCAC,FCFA=FBFC,
∵CF=4,tan∠BDC=tan∠BAC=BCAC=12,
∴AF=8,
∴48=FB4,解得FB=2,
设⊙O的半径为r,则AF=2r+2=8.
解之得r=3.
∵GH⊥AB,
∴∠GHB=90°.
∵∠DOE=90°,
∴∠GHB=∠DOE.
∴GH∥DO.
∴△BHG∽△BOD
∴BHBO=BGBD.
∵G为BD中点,
∴BG=12BD.
∴BH=12BO=32,GH=12OD=32.
∴AH=AB BH=6 32=92.
∴AG=GH2+AH2=(32)2+(92)2=3210.
【解析】【分析】(1)先求出 ,再求出 ,最后证明求解即可;
(2)根据题意先求出 , 再利用相似三角形的判定与性质求出 ,, 最后利用勾股定理计算求解即可。
22.【答案】(1)解:把代入抛物线,
得或,
点A在点B的左侧
A( 2a,0),B(3,0)
抛物线的函数表达式为:;
(2)解:由题意得:作,连接与轴交于点,
在与中,
,
,
,与轴的交点,即
,即,
得
设直线解析式为
将,代入得
解得:
直线解析式为;
点是直线与抛物线的交点,
则
解方程得:,(当时,点与点重合,故舍去)
将代入得:
点坐标为;
将直线沿轴翻折得到直线,与轴交于点,与抛物线交于点,
,设直线解析式为,
将与代入得
解得:
直线解析式为;
点是直线与抛物线的交点,
则
解方程得:,(当时,点与点重合,故舍去)
将代入得:
点坐标为;
点的坐标为,;
(3)解:的值为定值,定值是5.
【解析】【解答】解:(3)的值为定值,定值是5.
,,点到轴的距离为
和同底
点、到直线的距离相等,
,,
,
的值为定值,定值为5
【分析】(1)先求出 或, 再求出a=-1,最后求函数解析式即可;
(2)根据题意先求出 , 再利用待定系数法求函数解析式即可;
(3)先求出点、到直线的距离相等,再求出,最后利用全等三角形的判定与性质证明求解即可。
23.【答案】(1)解:∵是绕点O顺时针旋转得到的,,
∴,,
∴,
设直线的解析式为,
把和的坐标代入可得:
,
解得
∴直线的解析式为;
(2)解:∵,,
∴,
同(1)的方法,可求出直线的解析式为,
联立:,解得:,
∴,
∴;
(3)或
【解析】【解答】解:(3)存在, 理由如下,
由(1)知,直线的解析式为,
∴,
∵以点D、F、M、N为顶点的四边形是矩形,
∴是直角三角形,
①当时,则M只能在x轴上,连接交于点G,如下图,
设 而 ,,
∴ , , ,,
∵
∴
解得: 即
由平移的性质可得: 即
②当时,则M只能在y轴上,不符合题意舍去;
③当时,则可知M点为O点,如下图,
∵四边形为矩形,
∴,,
∴此时;
综上可知,存在满足条件的N点,其坐标为或.
【分析】(1)根据旋转的性质结合点B的坐标可得OD=OC=4,DE=BC=2,表示出点D的坐标,然后利用待定系数法就可求出直线BD的表达式;
(2)易得E(4,2),求出直线OE的解析式,联立直线BD的解析式求出x、y,得到点H的坐标,然后根据三角形的面积公式进行计算;
(3)易得F(0,),根据矩形的性质可得△DFM是直角三角形, ①当∠MDF=90°时,则M只能在x轴上,连接FN交MD于点G,设M(x,0),表示出OM、OF、OD、MD,根据勾股定理可求出x的值,表示出点M的坐标,然后根据平移的性质可得点N的坐标;②当∠MDF=90°时,则M只能在y轴上,不符合题意舍去; ③当∠FMD=90°时,则可知M点为O点,根据矩形的性质可得NF=OD=4,ND=OF=,据此可得点N的坐标.
一、单选题(共10题;共40分)
1.(4分)相反数为5的数是( )
A.-5 B.5 C.±5 D.
2.(4分)截至2022年10月,我国基本医疗保险参保人数已超过13.6亿人,其中数据13.6亿用科学记数法表示为( )
A. B. C. D.
3.(4分)下面计算正确的是( )
A.2x2+2x2=4x4 B.(x﹣y)2=x2﹣y2
C.﹣x2 (﹣x)2=x4 D.(﹣2x2)3=﹣8x6
4.(4分)如图所示的石板凳,它的俯视图是( )
A. B.
C. D.
5.(4分)如图,在同一条道路上,甲车从地到地,乙车从地到地,甲车和乙车同时匀速出发,甲车先到达目的地,图中的折线段表示甲、乙两车之间的距离(单位:km)与行驶时间(单位:h)的函数关系图象,下列说法错误的是( ).
A.甲、乙两车相遇时间为 B.甲车速度为
C.乙车速度为 D.甲车比乙车早
6.(4分) 如图,平行四边形的对角线与相交于点,,垂足为,,,,则的长为( )
A. B. C. D.
7.(4分)若关于的一元二次方程的一个根为,则的值为( )
A.3 B.0 C.-3 D.-3或3
8.(4分)在一个桌子上放着若干张背面向上的扑克牌,这些扑克牌背面图案相同,正面为3张方块、2张红桃和张梅花.若从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为,则的值为( )
A.4 B.5 C.6 D.7
9.(4分)如图,点A、C为反比例函数图象上的点,过点A、C分别作轴,轴,垂足分别为B、D,连接、、,线段交于点E,点E恰好为的中点,当的面积为6时,k的值为( )
A. B.8 C. D.
10.(4分)如图,在边长为3的正方形中,点E在边上,且.是以E为直角顶点的等腰直角三角形,分别交于点M,N,过点F作的垂线交的延长线于点G.连接,则下列结论错误的是( )
A. B. C. D.
二、填空题(共4题;共20分)
11.(5分)不等式的解集为 .
12.(5分)分解因式: .
13.(5分)如图,⊙O是△ABC的外接圆,∠A=30°,BC=4,则⊙O的直径为 .
14.(5分)如图,点O是正方形的中心,.中,,过点D.分别交于点G、M,连接.若, ,则的长 .
三、计算题(共1题;共8分)
15.(8分) 计算:.
四、作图题(共1题;共8分)
16.(8分)如图,三个顶点的坐标分别为.
( 1 )请画出向下平移5个单位长度后得到的;
( 2 )请画出关于y轴对称的.
五、解答题(共3题;共26分)
17.(8分)先化简,再求值: ,其中 .
18.(8分)清朝数学家梅文鼎的《方程论》中有这样一题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,每亩场地折实田多少?
译文为:若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?
19.(10分)消防车是灭火救灾的主要装备.如图1是一辆登高云梯消防车的实物图,图2是其工作示意图.当云梯升起时,与底盘的夹角为α,液压杆与底盘的夹角为β.已知液压杆m,当,时,求的长.(结果精确到m,参考数据:,,)
六、综合题(共4题;共48分)
20.(10分)幸福成都,美在文明!为助力成都争全国文明典范城市,某校采用四种宣传形式:A.宣传单宣传,B.电子屏宣传,C.黑板报宣传,D.志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
请结合图中所给信息,解答下列问题:
(1)(3分)本次调查的学生共有 人,请补全条形统计图;
(2)(3分)扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为 ;
(3)(4分)本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率
21.(12分)如图,是的直径,是弦,是的中点,与交于点,是延长线上的一点,且.
(1)(6分)求证:为的切线;
(2)(6分)连接,取的中点,连接.若,,求的长.
22.(12分)如图,抛物线交x轴于A、B两点(点A在点B的左侧),交y轴于C点,.
(1)(3分)求抛物线的函数表达式;
(2)(4分)如图1,连接BC,点P在抛物线上,且,求点P的坐标;
(3)(5分)如图2,M是抛物线上一点,N为射线CB上的一点,且M、N两点均在第一象限内,B、N是位于直线AM同侧的不同两点,,点M到x轴的距离为2L,的面积为5L,且,请问的长是否为定值?如果是,请直接写出这个定值;如果不是,请说明理由.
23.(14分)如图,四边形是矩形,点A、C分别在x轴、y轴上,是绕点O顺时针旋转得到的,点D在x轴上,直线交y轴于点F,交于点H,点B的坐标为.
(1)(4分)求直线的表达式;
(2)(4分)求的面积;
(3)(6分)点M在x轴上,平面内处否存在点N,使以点D、F、M、N为顶点的四边形是矩形 若存在,请直接写出点N的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:相反数为-5.
故答案为:A.
【分析】只有符号不同的两个数叫做互为相反数,据此解答即可.
2.【答案】B
【解析】【解答】13.6亿,
故答案为:B.
【分析】 把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数,n是正整数),这种计数法叫做科学记数法。根据科学记数法的定义计算求解即可。
3.【答案】D
【解析】【解答】解:A、2x2+2x2=4x2,原式计算错误,故答案为:不符合题意;
B、(x﹣y)2=x2﹣2xy+y2,原式计算错误,故答案为:不符合题意;
C、﹣x2 (﹣x)2=﹣x2 x2=﹣x4,原式计算错误,故答案为:不符合题意;
D、(﹣2x2)3=﹣8x6,原式计算正确,故答案为:符合题意.
故答案为:D.
【分析】根据合并同类项、完全平方公式、同底数幂的乘法、幂的乘方与积的乘方分别计算,再判断即可.
4.【答案】D
【解析】【解答】解:俯视图是从物体的上面看得到的平面图形,该几何体从上面看到的是 .
故答案为:D.
【分析】利用三视图的定义求解即可。
5.【答案】D
【解析】【解答】解:A.出发1小时后,两车相距为零,即两车相遇,故不符合题意;
B.甲车速度为,故不符合题意;
C.乙车速度为,故不符合题意;
D.甲车比乙车早,故符合题意;
故答案为:D.
【分析】根据所给的函数图象,结合题意,对每个选项一一判断即可。
6.【答案】D
【解析】【解答】解:四边形为平行四边形,,,
,,
,
,
为直角三角形,且,
,
,
,
解得.
故答案为:D.
【分析】根据平行四边形的性质可得OA=AC=1,OB=BD=,由勾股定理逆定理知△AOB为直角三角形,且∠BAO=90°,利用勾股定理可求出BC的值,然后根据等面积法进行计算.
7.【答案】C
【解析】【解答】解:关于的一元二次方程的一个根为0,
∴m2-9=0且m-3≠0
解之:m=±3,m≠3,
∴m=-3.
故答案为:C
【分析】利用一元二次方程的定义,可知m-3≠0,将x=0代入方程,可得到m2-9=0,分别求解,可求出m的值.
8.【答案】B
【解析】【解答】解:根据题意得:
,
解得:,
故答案为:B.
【分析】根据题意先求出 从这些打乱的扑克牌中任意摸出1张扑克牌,这张扑克牌是梅花的概率为, 列方程,再求解即可。
9.【答案】A
【解析】【解答】解:设点C的坐标为,则点,,,,
,
.
故答案为:A.
【分析】设C(m,),则E(m,),A(m,),根据三角形的面积公式可得S△AEC=BD·AE=k=6,求解可得k的值.
10.【答案】D
【解析】【解答】A、∵边长为3的正方形,
∴,
∴;
∵是以E为直角顶点的等腰直角三角形,
∴,不符合题意;
B、∵边长为3的正方形, ,
∴,
∵是以E为直角顶点的等腰直角三角形,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴,不符合题意;
C、过点F作于点H,
∵,
∴四边形是正方形,
∴,
∵,,
∴,,
∴,
∴,
∴,
∴,不符合题意;
D、∵,
∴,
∴,符合题意;
故答案为:D.
【分析】由AB=3,AE=2,利用勾股定理求出BE==EF,据此判断A;根据AAS证明△BAE≌△EGF,可得AB=EG=3,AE=GF=2,从而求出DG=EG-DE=2,利用勾股定理求出DF的长,即可判断B;过点F作于点H,证四边形DGFH为正方形,可得DH=2,CH=1,再证△HFN∽△CBN,△DEM∽△HFN,利用相似三角形的性质求出CN、HN、HM、MN,即可判断C、D。
11.【答案】x≤2
【解析】【解答】解:,
移项合并得:,
化系数为1得:x≤2,
故答案为:x≤2.
【分析】利用不等式的性质及不等式的解法求出解集即可。
12.【答案】(2b+a)(2b-a)
【解析】【解答】解:,
故答案为:(2b+a)(2b-a).
【分析】利用加法交换律把多项式整理成两个因式平方差的形式,进而利用平方差公式直接分解因式即可.
13.【答案】8
【解析】【解答】解:如图,连接OB,OC,
∵∠A=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
又∵BC=4,
∴BO=CO=BC=BC=4,
∴⊙O的直径为8,
故答案为:8.
【分析】连接OB,OC,依据△BOC是等边三角形,即可得到BO=CO=BC=BC=4,进而得出⊙O的直径为8.
14.【答案】
【解析】【解答】解:如图,过点F作于点H,
正方形ABCD,
,,
,
,
,,
,,
,
,
,
,
故答案为:.
【分析】利用正方形的性质求出,,再求出,最后利用全等三角形的判定与性质,勾股定理计算求解即可。
15.【答案】解:
【解析】【分析】根据特殊角三角函数值、绝对值、开立方、乘方先计算,再计算加减即可.
16.【答案】解:( 1 )如图,即为所求.
( 2 )如图,即为所求.
【解析】【分析】(1)分别将点A、B、C向下平移5个单位长度得到点A1、B1、C1的位置,然后顺次连接即可;
(2)关于y轴对称的点,横坐标互为相反数,纵坐标相同,据此找出点A2、B2、C2的位置,然后顺次连接即可.
17.【答案】解:原式=
=
= ,
当 , 时,
原式= .
【解析】【分析】根据单项式与多项式的乘法法则、完全平方公式、平方差公式分别去括号,再合并同类项对原式进行化简,然后将a、b的值代入进行计算.
18.【答案】解:设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩.
可列方程组为
解得
答:每亩山田相当于实田0.9亩,每亩场地相当于实田 亩.
【解析】【分析】 设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩,根据“若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩”列出方程组,求解即可.
19.【答案】解:在中,,m.
,
,
∴,∴m.
,
,m.
在中,
,
,
m.
∴m.
答:的长约为m.
【解析】【分析】结合题意,利用锐角三角函数计算求解即可。
20.【答案】(1)50
补全条形统计图如图所示:
(2)108°
(3)解:列表得:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中恰好是甲和乙的有2种,
∴被选取的两人恰好是甲和乙的概率是.
【解析】【解答】解:(1)本次调查的学生共有:(人),
喜欢B.电子屏宣传的人数有:(人),
补全条形统计图如图所示:
故答案为:50
(2)“D.志愿者宣传”对应的扇形圆心角度数为;
故答案为:;
【分析】(1)利用C的人数除以所占的比例可得总人数,然后求出B的人数,进而可补全条形统计图;
(2)利用D的人数除以总人数,然后乘以360°可得所占扇形圆心角的度数;
(3)画出表格,找出总情况数以及恰好是甲和乙的情况数,然后根据概率公式进行计算.
21.【答案】(1)证明:如图1,连接,.
∵,
∴.
∵,
∴.
∵∠OED=∠FEC,
∴∠OED=∠FCE.
∵AB是⊙O的直径,D是AB 的中点,
∴∠DOE=90°.
∴∠OED+∠ODC=90°.
∴∠FCE+∠OCD=90°,即∠OCF=90°.
∴OC⊥CF.
∴CF为⊙O的切线.
(2)解:如图2,连接BC,过G作GH⊥AB,垂足为H.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OBC+∠FAC=90°,
∵OC=OB,
∴∠OBC=∠OCB,
∵∠FCO=∠FCB+∠OCB=90°,
∴∠FCB=∠FAC,
∵∠F=∠F,
∴△FCB∽△FAC,
∴FCFA=BCAC,FCFA=FBFC,
∵CF=4,tan∠BDC=tan∠BAC=BCAC=12,
∴AF=8,
∴48=FB4,解得FB=2,
设⊙O的半径为r,则AF=2r+2=8.
解之得r=3.
∵GH⊥AB,
∴∠GHB=90°.
∵∠DOE=90°,
∴∠GHB=∠DOE.
∴GH∥DO.
∴△BHG∽△BOD
∴BHBO=BGBD.
∵G为BD中点,
∴BG=12BD.
∴BH=12BO=32,GH=12OD=32.
∴AH=AB BH=6 32=92.
∴AG=GH2+AH2=(32)2+(92)2=3210.
【解析】【分析】(1)先求出 ,再求出 ,最后证明求解即可;
(2)根据题意先求出 , 再利用相似三角形的判定与性质求出 ,, 最后利用勾股定理计算求解即可。
22.【答案】(1)解:把代入抛物线,
得或,
点A在点B的左侧
A( 2a,0),B(3,0)
抛物线的函数表达式为:;
(2)解:由题意得:作,连接与轴交于点,
在与中,
,
,
,与轴的交点,即
,即,
得
设直线解析式为
将,代入得
解得:
直线解析式为;
点是直线与抛物线的交点,
则
解方程得:,(当时,点与点重合,故舍去)
将代入得:
点坐标为;
将直线沿轴翻折得到直线,与轴交于点,与抛物线交于点,
,设直线解析式为,
将与代入得
解得:
直线解析式为;
点是直线与抛物线的交点,
则
解方程得:,(当时,点与点重合,故舍去)
将代入得:
点坐标为;
点的坐标为,;
(3)解:的值为定值,定值是5.
【解析】【解答】解:(3)的值为定值,定值是5.
,,点到轴的距离为
和同底
点、到直线的距离相等,
,,
,
的值为定值,定值为5
【分析】(1)先求出 或, 再求出a=-1,最后求函数解析式即可;
(2)根据题意先求出 , 再利用待定系数法求函数解析式即可;
(3)先求出点、到直线的距离相等,再求出,最后利用全等三角形的判定与性质证明求解即可。
23.【答案】(1)解:∵是绕点O顺时针旋转得到的,,
∴,,
∴,
设直线的解析式为,
把和的坐标代入可得:
,
解得
∴直线的解析式为;
(2)解:∵,,
∴,
同(1)的方法,可求出直线的解析式为,
联立:,解得:,
∴,
∴;
(3)或
【解析】【解答】解:(3)存在, 理由如下,
由(1)知,直线的解析式为,
∴,
∵以点D、F、M、N为顶点的四边形是矩形,
∴是直角三角形,
①当时,则M只能在x轴上,连接交于点G,如下图,
设 而 ,,
∴ , , ,,
∵
∴
解得: 即
由平移的性质可得: 即
②当时,则M只能在y轴上,不符合题意舍去;
③当时,则可知M点为O点,如下图,
∵四边形为矩形,
∴,,
∴此时;
综上可知,存在满足条件的N点,其坐标为或.
【分析】(1)根据旋转的性质结合点B的坐标可得OD=OC=4,DE=BC=2,表示出点D的坐标,然后利用待定系数法就可求出直线BD的表达式;
(2)易得E(4,2),求出直线OE的解析式,联立直线BD的解析式求出x、y,得到点H的坐标,然后根据三角形的面积公式进行计算;
(3)易得F(0,),根据矩形的性质可得△DFM是直角三角形, ①当∠MDF=90°时,则M只能在x轴上,连接FN交MD于点G,设M(x,0),表示出OM、OF、OD、MD,根据勾股定理可求出x的值,表示出点M的坐标,然后根据平移的性质可得点N的坐标;②当∠MDF=90°时,则M只能在y轴上,不符合题意舍去; ③当∠FMD=90°时,则可知M点为O点,根据矩形的性质可得NF=OD=4,ND=OF=,据此可得点N的坐标.
同课章节目录
