2.1 锐角三角比 初中数学九年级上册青岛版课件(共35张PPT)
文档属性
| 名称 | 2.1 锐角三角比 初中数学九年级上册青岛版课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 75.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
第2章
解直角三角形
2 . 1
锐角三角比
学习目标
1. 经历锐角三角比的概念的探究.
2. 正确理解三角比符号的含义,掌握锐角三角比的
表示方法.
3. 能根据定义求锐角的三角比.
实验与探究
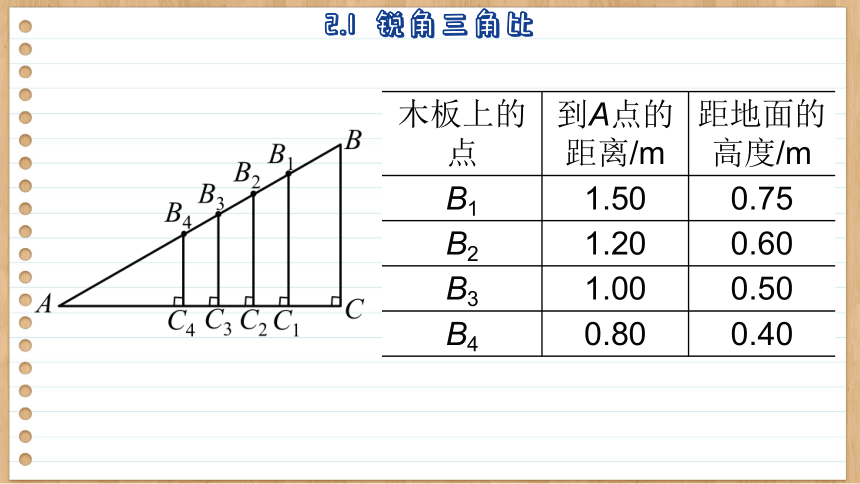
(1)有一块长2.00 m的平滑木板AB,小亮将它的一端B架高1m,另一端A放在平地上(图2-1),在木板上分别取点 B1,B2,B3,B4,分别量得它们到A点的距离 AB1,AB2,AB3,AB4,以及它们距地面的高度 B1C1,B2C2,B3C3,B4C4,数据如下表所示:
木板上的点 到A点的距离/m 距地面的高度/m
B1 1.50 0.75
B2 1.20 0.60
B3 1.00 0.50
B4 0.80 0.40
利用上述数据,分别计算比值,,,,,你有什么发现
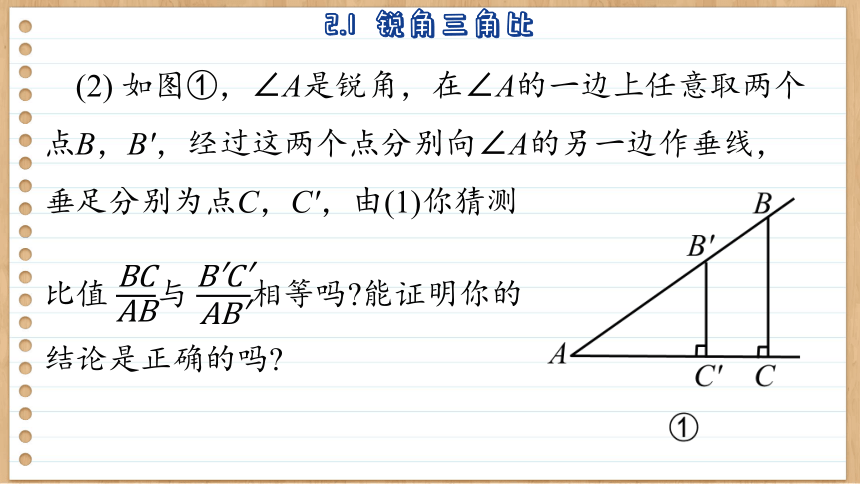
(2) 如图①,∠A是锐角,在∠A的一边上任意取两个点B,B′,经过这两个点分别向∠A的另一边作垂线,垂足分别为点C,C′,由(1)你猜测
比值 与 相等吗 能证明你的
结论是正确的吗
因为∠A=∠A′,∠BCA=∠B′C′A=90°,
所以 Rt△ABC∽Rt△AB′C′,
因此 = .
(3) 如果设比值 = k,由 (2)你发现当锐角A的大小确定后,k的大小与点B′在AB边上的位置有关吗
无关
(4) 如图②,以4为端点,在锐角A的内部(或外部)作一条射线在这条射线上取点B′′,使AB′′=AB,这样又得到了一个锐角∠B′′AC过B′′作 B′′C′′⊥AC,垂足为点C′′. 比值 与k相等吗 为什么 由此你得到怎样的结论
对于确定的锐角A来说,比值k与点B在AB边上的位置无关,只与锐角A的大小有关.
加油站
≠k,假设 = ,由AB′′=AB′,可得B′′C′′ = B′C′. 因为∠AC′B′ = ∠AC′′B′′ = 90°,于是Rt△AB′C′ ≌ Rt△AB′′C′′,则∠B′AC′= ∠B′′AC′′但这与∠B′AC′ ≠ ∠B′′AC′′矛盾.
由上面的探索,我们可以利用 Rt△ABC (图2-3)把比值k记作 ,当锐角A的大小确定后,不论以∠A 为锐角的直角三角形的大小如何,这个比值也就随之确定,
我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即
sinA=
类似地,当锐角A的大小确定后,比值和比值也随之确定. 我们把锐角A的邻边与斜边的比叫做∠A 的余弦 (cosine ),记作cosA,即
cosA=
把锐角A的对边与邻边的比叫做∠A的正切 (tangent),记作tan A,即
tanA=
锐角A的正弦、余弦、正切统称锐角A的三角比.
tanA=
cosA=
sinA=
小资料
在Rt△ABC中,∠C=90°,如果用a,b分别表示∠A的对边和邻边,c 表示斜边.那么sinA=,cosA=,tanA= .
sinA,cosA,tanA 分别是一个完整的记号.当角只用一个大写字母或小写字母表示时,习惯上在记号中省去角的符号“∠”,不能理解成 sin·A,cos·A,tan·A.
在图中,把∠A的对边记作a,∠B的对边记作b,∠C的对边记作c,你能分别用a,b,c表示∠A和∠B的正弦、余弦和正切吗
例 1
如图,在Rt△ABC中∠C=90°,a=2,b=4. 求∠A的正弦、余弦、正切的值.
如图,在Rt△ABC中,∠C=90°.
∵ a=2,b=4,
∴ c=== 2.
sinA=,
cosA= = ,
tanA== .
练 习
1. 如果Rt△ABC ∽ Rt△A′B′C′,∠C = ∠C′ = 90°,
sinA 等于sinA′ 吗 为什么 cosA 与cosA′ 呢
2. 如图,在Rt△ABC中,∠C=90°,c=3,a=2,
求∠A的正弦、余弦、正切的值.
习题 2.1
复习与巩固
l. 在Rt△ABC中,∠C=90°,根据下列条件求出 ∠A和∠B的正弦、余弦的值:
(1) a=1,b=;
(2) b=,c=4.
2. 在Rt△ABC中,∠C=90°,AB=2AC,求cosB 和
tanA 的值.
3. 在Rt△ABC中,∠C=90°,BC=8,sinA=,求
cosA和tanB的值.
拓展与延伸
4. 如图,在Rt△ABC中,∠C=90°,AC=4,点D,E
在BC上,BD=5,DE=2,EC=3.
设∠ABC=α ,∠ADC= β ,∠AEC= γ ,
求tanα ,cosβ ,sinγ 的值.
5. 在Rt△ABC中,∠C=90°,tanA=,求AC∶BC∶AB
的值.
探索与创新
6. 已知等腰三角形中,两边的长分别为 10 cm和16 cm,
求它的底角的正弦、余弦和正切的值.
本课结束
This lesson is over
THANKS!
第2章
解直角三角形
2 . 1
锐角三角比
学习目标
1. 经历锐角三角比的概念的探究.
2. 正确理解三角比符号的含义,掌握锐角三角比的
表示方法.
3. 能根据定义求锐角的三角比.
实验与探究
(1)有一块长2.00 m的平滑木板AB,小亮将它的一端B架高1m,另一端A放在平地上(图2-1),在木板上分别取点 B1,B2,B3,B4,分别量得它们到A点的距离 AB1,AB2,AB3,AB4,以及它们距地面的高度 B1C1,B2C2,B3C3,B4C4,数据如下表所示:
木板上的点 到A点的距离/m 距地面的高度/m
B1 1.50 0.75
B2 1.20 0.60
B3 1.00 0.50
B4 0.80 0.40
利用上述数据,分别计算比值,,,,,你有什么发现
(2) 如图①,∠A是锐角,在∠A的一边上任意取两个点B,B′,经过这两个点分别向∠A的另一边作垂线,垂足分别为点C,C′,由(1)你猜测
比值 与 相等吗 能证明你的
结论是正确的吗
因为∠A=∠A′,∠BCA=∠B′C′A=90°,
所以 Rt△ABC∽Rt△AB′C′,
因此 = .
(3) 如果设比值 = k,由 (2)你发现当锐角A的大小确定后,k的大小与点B′在AB边上的位置有关吗
无关
(4) 如图②,以4为端点,在锐角A的内部(或外部)作一条射线在这条射线上取点B′′,使AB′′=AB,这样又得到了一个锐角∠B′′AC过B′′作 B′′C′′⊥AC,垂足为点C′′. 比值 与k相等吗 为什么 由此你得到怎样的结论
对于确定的锐角A来说,比值k与点B在AB边上的位置无关,只与锐角A的大小有关.
加油站
≠k,假设 = ,由AB′′=AB′,可得B′′C′′ = B′C′. 因为∠AC′B′ = ∠AC′′B′′ = 90°,于是Rt△AB′C′ ≌ Rt△AB′′C′′,则∠B′AC′= ∠B′′AC′′但这与∠B′AC′ ≠ ∠B′′AC′′矛盾.
由上面的探索,我们可以利用 Rt△ABC (图2-3)把比值k记作 ,当锐角A的大小确定后,不论以∠A 为锐角的直角三角形的大小如何,这个比值也就随之确定,
我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即
sinA=
类似地,当锐角A的大小确定后,比值和比值也随之确定. 我们把锐角A的邻边与斜边的比叫做∠A 的余弦 (cosine ),记作cosA,即
cosA=
把锐角A的对边与邻边的比叫做∠A的正切 (tangent),记作tan A,即
tanA=
锐角A的正弦、余弦、正切统称锐角A的三角比.
tanA=
cosA=
sinA=
小资料
在Rt△ABC中,∠C=90°,如果用a,b分别表示∠A的对边和邻边,c 表示斜边.那么sinA=,cosA=,tanA= .
sinA,cosA,tanA 分别是一个完整的记号.当角只用一个大写字母或小写字母表示时,习惯上在记号中省去角的符号“∠”,不能理解成 sin·A,cos·A,tan·A.
在图中,把∠A的对边记作a,∠B的对边记作b,∠C的对边记作c,你能分别用a,b,c表示∠A和∠B的正弦、余弦和正切吗
例 1
如图,在Rt△ABC中∠C=90°,a=2,b=4. 求∠A的正弦、余弦、正切的值.
如图,在Rt△ABC中,∠C=90°.
∵ a=2,b=4,
∴ c=== 2.
sinA=,
cosA= = ,
tanA== .
练 习
1. 如果Rt△ABC ∽ Rt△A′B′C′,∠C = ∠C′ = 90°,
sinA 等于sinA′ 吗 为什么 cosA 与cosA′ 呢
2. 如图,在Rt△ABC中,∠C=90°,c=3,a=2,
求∠A的正弦、余弦、正切的值.
习题 2.1
复习与巩固
l. 在Rt△ABC中,∠C=90°,根据下列条件求出 ∠A和∠B的正弦、余弦的值:
(1) a=1,b=;
(2) b=,c=4.
2. 在Rt△ABC中,∠C=90°,AB=2AC,求cosB 和
tanA 的值.
3. 在Rt△ABC中,∠C=90°,BC=8,sinA=,求
cosA和tanB的值.
拓展与延伸
4. 如图,在Rt△ABC中,∠C=90°,AC=4,点D,E
在BC上,BD=5,DE=2,EC=3.
设∠ABC=α ,∠ADC= β ,∠AEC= γ ,
求tanα ,cosβ ,sinγ 的值.
5. 在Rt△ABC中,∠C=90°,tanA=,求AC∶BC∶AB
的值.
探索与创新
6. 已知等腰三角形中,两边的长分别为 10 cm和16 cm,
求它的底角的正弦、余弦和正切的值.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
