2.3 用计算器求锐角三角比 -初中数学九年级上册青岛版课件(共38张PPT)
文档属性
| 名称 | 2.3 用计算器求锐角三角比 -初中数学九年级上册青岛版课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 101.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 06:55:10 | ||
图片预览











文档简介
(共38张PPT)
第2章
解直角三角形
2 . 3
用计算器求锐角三角比
学习目标
1. 理解相似三角形周长的比等于相似比,面积的比等于相似比的平方,相似三角形对应高的比也等于相似比;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2. 能应用相似三角形的有关性质解决相关问题.
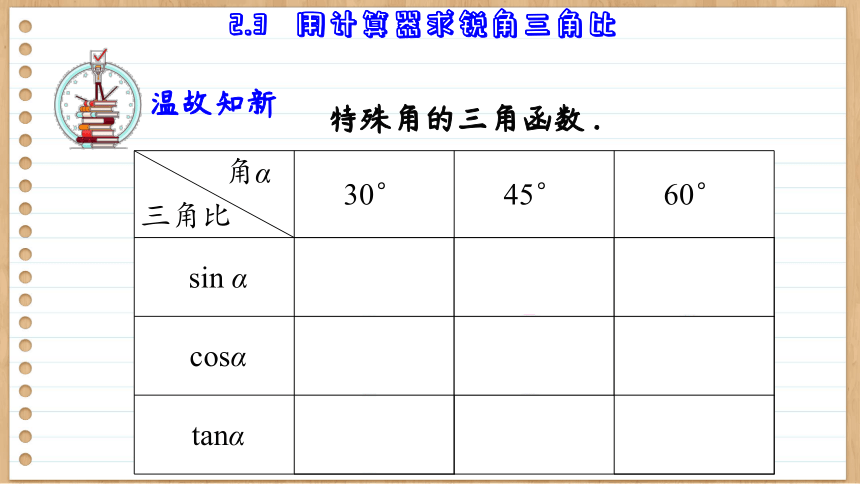
特殊角的三角函数.
角α 三角比 30° 45° 60°
sin α
cosα
tanα 1
温故知新
实验与探究
根据锐角三角比的定义,可以求出 30°,45°,60°这些特殊角的正弦、余弦、正切的值怎样才能知道任意一个锐角的三角比呢
用科学计算器可以解决这个问题.
打开科学计算器,启动开机键后,使显示器的上方显示 DEG(如果没有显示 DEG,可以按 DR 1 键),表示计算器已经进入以“度”为角的度量单位的运算状态. 这时,按相应的三角比的名称键,再输入锐角的度数,按[ = 键后,显示器显示的数字即为该锐角相应的三角比的值(或精确到10-9的近似值).因计算器的种类不同,键盘上各键的功能符号和按键顺序可能不同.使用计算器前,应先阅读使用说明书,以免使用中出现计算错误.
例 1
用计算器求下列锐角三角比的值 (精确到0.000 1):
sin 47°; (2) cos 56.3°;
(3) sin 25°31′48′′; (4) tan35°10′22′′.
在角的度量单位为“度”的状态下(显示器上方显示 DEG)
(1) sin 47°;
按下列顺序依次按键:
sin 47 DMS = ,
屏幕上显示0.731353 701,按精确到0.0001取近似值,得sin 47° ≈ 0.7314;
(2) cos 56.3°;
按下列顺序依次按键:
cos 47 3 DMS = ,
屏幕上显示 0.554 844 427,按精确到0.000 1取近似值,得cos 56.3°≈ 0.554 8;
(3) sin 25°31′48′′;
按下列顺序依次按键:
sin 25 DMS 31 DMS 48 DMS = ,
屏慕上显示0.430983 63按精确到0.0001取近似值得 sin25°31′48′′≈0.4310;
(4) tan35°10′22′′.
按下列顺序依次按键:
sin 35 DMS 10 DMS 22 DMS = ,
屏幕上显示 0.704 711093,按精确到0.0001取近似值,得tan35°10′22′′ ≈ 0.704 7.
例 2
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1) tan()°
按下列顺序依次按键:
tan ( 80 ÷ 3 ) DMS = ,
屏幕上显示0.502 218 876,按精确到0.0001取近似值,得tan ()°≈0.502 0;
(2) sin 9°
按下列顺序依次按键:
sin 0 DMS 9 DMS = ,
屏幕上显示 2.617 990 887×10-3,按精确到0.0001取近似值,得sin9′≈0.0026.
挑战自我
利用计算器求下列锐角三角比的值,填写下表:
角α 三角比 1° 10° 20° 30° 40° 45°
sinα 0.017 5 0.173 6 0.342 0 0.5 0.642 8 0.707 1
cosα 0.999 8 0.984 8 0.939 7 0.866 0 0.766 0 0.707 1
角α 三角比 50° 60° 70° 80° 89°
sinα 0.766 0 0.866 0 0.939 7 0.984 8 0.999 8
cosα 0.642 8 0.5 0.342 0 0.173 6 0.017 5
观察上表,并回答下列问题:
(1)当锐角逐渐增大时,它的正弦和余弦的值分别发生怎样的变化
当锐角 α 逐渐增大时,它的正弦值也逐渐增大,由接近于 0 逐渐增大至接近于 1;
当锐角 α 逐渐增大时它的余弦值逐渐减小,由接近于 1逐渐减小至接近于0.
(2)你能估计出锐角的正弦值的范围吗 锐角的余弦值
的范围呢?
0<sin α<1.
0<cos α<1.
(3) 你还能从表中发现什么规律
还可以发现:
①当 α<45°时,sin α<cos α;
当45°<α<90°时,sin α>cos α.
② sin α=cos(90°-α),
cos α=sin(90°-α)
练 习
1. 用计算器求下列锐角三角比的值:
(1) sin 75°; (2) cos 35.7°;
(3) tan ()°; (4) sin 75.61°.
≈ 0.965 9.
≈ 0.812 1.
≈ 1.592 6.
≈ 0.968 6.
2. 用计算器求下列锐角三角比的值:
(1) sin 53°49′; (2) sin 30°4′56′′ ;
(3) cos 55′; (4) tan 72°8′′.
≈ 0.807 1.
≈ 0.501 2.
≈ 0.999 9.
≈ 3.078 1.
已知锐角 A三角比的值,如何利用计算器求出锐角A呢
启动开机键后,在角的度量单位为“度”的状态下,先按副功能键 2ndF 和相应三角比的名称键,再输入三角比的值,按 = 键后,屏慕上就可以显示以度为单位的锐角.
例 3
根据下列三角比的值,用计算器求相应的锐角A(精确到1′′):
(1) sin A = 0.618 5;
(2) tan A = 3.207 8.
在角的度量单位为“度”的状态下,
(1) sin A = 0.618 5;
按下列顺序依次按键;
2ndF sin 0 6185 =,
屏幕上显示38.206 679 08°,
即锐角A=38.206 679 08°.
再按 DMs 键,将它换算成“度、分、秒”的形式,
屏幕上显示38°12′24.04′′,
所以锐角A ≈ 38°12′24′′;
(2) tan A = 3.207 8.
按下列顺序依次按键;
2ndF tan 3 2078 =,
屏幕上显示72.685 647 68°,
即锐角A ≈ 72.685 647 68°.
再按 DMs 键,将它换算成“度、分、秒”的形式,
屏幕上显示 72°41′8.33′′,
所以锐角A ≈ 72°41′8.33′′ .
例 4
利用计算器求下列各式的值:
(1) sin 20° tan 35° ;
(2) sin30°26′ = cos45°30′8′′.
在角的度量单位为“度”的状态下,
(1) sin 20° tan 35° ;
按下列顺序依次按键:
sin 20 DMS × tan 35 DMS = ,
屏幕上显示 0.239 485 082,
所以 sin 20° tan35°≈ 0.239 5;
(2) sin30°26′ = cos45°30′8′′.
按下列顺序依次按键:
1 ab/c 2 × sin 30 DMS 26 DMS + . 2 ÷ 2 ×
cos 45 DMS 30 DMS 8 DMS = ,,
屏幕上显示0.748 865 866.
所以sin30°26′+ cos45°30′8′′ ≈0.748 9.
练 习
1. 根据下列三角比的值,用计算器求相应的锐角α , β :
(1) sin α = 0.297 4;
(2) cosα = 0.785 7;
(3) tan β = .
α≈ 17°18′5″.
α≈ 38°12′52″.
β ≈ 18°26′6″.
2. 利用计算器求下列各式的值:
(1) tan 15°· cos 28° - tan 43°;
(2) cos 32°+ tan 50° + sin 40°.
≈ -0.695 9.
≈ 2.682 6.
习题 2.3
复习与巩固
1. 用计算器求下列锐角三角比的值:
(1) sin 45°, cos 35°,
tan 52°, sin 13.6° ,
cos 25.5° ;
≈ 0.707 1.
≈ 0.819 2.
≈ 1.279 9.
≈ 0.235 1.
≈ 0.902 6.
(2) sin3°12′, cos80°25′,
tan75°36′, sin56°12′10′′,
tan31°30′21′′, sin50′23′′.
≈ 0.055 8.
≈ 0.166 5.
≈ 3.894 7.
≈ 0.831 0.
≈ 0.612 9.
≈ 0.014 7.
2. 根据下列三角比的值,用计算器求相应的锐角α:
sinα=0.6; (2) sinα= 0.650 7;
(3) cosα= 0.13; (4) cosα=0.265 9;
(5) tanα=11.82; (6) tanα =0.370 5.
α≈ 36°52′12″.
α≈ 40°35′40″.
α≈ 82°31′49″.
α≈ 74°34′46″.
α≈ 85°9′51″.
α≈ 20°19′47″.
3. 利用计算器,求下列各式的值:
(1) cos 68°12′ + sin 42°- tan35°38′;
(2) .
≈ -0.058 0.
≈ -16.242 6.
拓展与延伸
4. 用计算器分别求出下列三组三角比的值:
sin 13°,cos77°;sin 62°18′,cos 27°42′;
sin 83°21′,cos 6°39′.
由此你发现了什么规律
解:sin 13°=cos 77°≈0.225 0;
sin 62°18′=cos 27°42′≈ 0.885 4;
sin 83°21'=cos 6°39′≈0.993 3.
如果 α,β 均为锐角,且α+β=90°,
那么sinα=cosβ,cosα=sinβ.
探索与创新
5. 利用本节“挑战自我”中的发现,不用计算器,比较
下列三个数的大小:
sin 62°,cos 62°, .
解:∵cos 62°-sin(90°-62°)-sin28°,
=sin 60°
且 62°>60°>28°
∴ sin 62°>sin 60°>sin 28°,
即 sin 62° > > cos 62°
本课结束
This lesson is over
THANKS!
第2章
解直角三角形
2 . 3
用计算器求锐角三角比
学习目标
1. 理解相似三角形周长的比等于相似比,面积的比等于相似比的平方,相似三角形对应高的比也等于相似比;多边形的周长的比等于相似比,面积的比等于相似比的平方.
2. 能应用相似三角形的有关性质解决相关问题.
特殊角的三角函数.
角α 三角比 30° 45° 60°
sin α
cosα
tanα 1
温故知新
实验与探究
根据锐角三角比的定义,可以求出 30°,45°,60°这些特殊角的正弦、余弦、正切的值怎样才能知道任意一个锐角的三角比呢
用科学计算器可以解决这个问题.
打开科学计算器,启动开机键后,使显示器的上方显示 DEG(如果没有显示 DEG,可以按 DR 1 键),表示计算器已经进入以“度”为角的度量单位的运算状态. 这时,按相应的三角比的名称键,再输入锐角的度数,按[ = 键后,显示器显示的数字即为该锐角相应的三角比的值(或精确到10-9的近似值).因计算器的种类不同,键盘上各键的功能符号和按键顺序可能不同.使用计算器前,应先阅读使用说明书,以免使用中出现计算错误.
例 1
用计算器求下列锐角三角比的值 (精确到0.000 1):
sin 47°; (2) cos 56.3°;
(3) sin 25°31′48′′; (4) tan35°10′22′′.
在角的度量单位为“度”的状态下(显示器上方显示 DEG)
(1) sin 47°;
按下列顺序依次按键:
sin 47 DMS = ,
屏幕上显示0.731353 701,按精确到0.0001取近似值,得sin 47° ≈ 0.7314;
(2) cos 56.3°;
按下列顺序依次按键:
cos 47 3 DMS = ,
屏幕上显示 0.554 844 427,按精确到0.000 1取近似值,得cos 56.3°≈ 0.554 8;
(3) sin 25°31′48′′;
按下列顺序依次按键:
sin 25 DMS 31 DMS 48 DMS = ,
屏慕上显示0.430983 63按精确到0.0001取近似值得 sin25°31′48′′≈0.4310;
(4) tan35°10′22′′.
按下列顺序依次按键:
sin 35 DMS 10 DMS 22 DMS = ,
屏幕上显示 0.704 711093,按精确到0.0001取近似值,得tan35°10′22′′ ≈ 0.704 7.
例 2
用计算器求下列锐角三角比的值(精确到 0.000 1):
(1) tan()°
按下列顺序依次按键:
tan ( 80 ÷ 3 ) DMS = ,
屏幕上显示0.502 218 876,按精确到0.0001取近似值,得tan ()°≈0.502 0;
(2) sin 9°
按下列顺序依次按键:
sin 0 DMS 9 DMS = ,
屏幕上显示 2.617 990 887×10-3,按精确到0.0001取近似值,得sin9′≈0.0026.
挑战自我
利用计算器求下列锐角三角比的值,填写下表:
角α 三角比 1° 10° 20° 30° 40° 45°
sinα 0.017 5 0.173 6 0.342 0 0.5 0.642 8 0.707 1
cosα 0.999 8 0.984 8 0.939 7 0.866 0 0.766 0 0.707 1
角α 三角比 50° 60° 70° 80° 89°
sinα 0.766 0 0.866 0 0.939 7 0.984 8 0.999 8
cosα 0.642 8 0.5 0.342 0 0.173 6 0.017 5
观察上表,并回答下列问题:
(1)当锐角逐渐增大时,它的正弦和余弦的值分别发生怎样的变化
当锐角 α 逐渐增大时,它的正弦值也逐渐增大,由接近于 0 逐渐增大至接近于 1;
当锐角 α 逐渐增大时它的余弦值逐渐减小,由接近于 1逐渐减小至接近于0.
(2)你能估计出锐角的正弦值的范围吗 锐角的余弦值
的范围呢?
0<sin α<1.
0<cos α<1.
(3) 你还能从表中发现什么规律
还可以发现:
①当 α<45°时,sin α<cos α;
当45°<α<90°时,sin α>cos α.
② sin α=cos(90°-α),
cos α=sin(90°-α)
练 习
1. 用计算器求下列锐角三角比的值:
(1) sin 75°; (2) cos 35.7°;
(3) tan ()°; (4) sin 75.61°.
≈ 0.965 9.
≈ 0.812 1.
≈ 1.592 6.
≈ 0.968 6.
2. 用计算器求下列锐角三角比的值:
(1) sin 53°49′; (2) sin 30°4′56′′ ;
(3) cos 55′; (4) tan 72°8′′.
≈ 0.807 1.
≈ 0.501 2.
≈ 0.999 9.
≈ 3.078 1.
已知锐角 A三角比的值,如何利用计算器求出锐角A呢
启动开机键后,在角的度量单位为“度”的状态下,先按副功能键 2ndF 和相应三角比的名称键,再输入三角比的值,按 = 键后,屏慕上就可以显示以度为单位的锐角.
例 3
根据下列三角比的值,用计算器求相应的锐角A(精确到1′′):
(1) sin A = 0.618 5;
(2) tan A = 3.207 8.
在角的度量单位为“度”的状态下,
(1) sin A = 0.618 5;
按下列顺序依次按键;
2ndF sin 0 6185 =,
屏幕上显示38.206 679 08°,
即锐角A=38.206 679 08°.
再按 DMs 键,将它换算成“度、分、秒”的形式,
屏幕上显示38°12′24.04′′,
所以锐角A ≈ 38°12′24′′;
(2) tan A = 3.207 8.
按下列顺序依次按键;
2ndF tan 3 2078 =,
屏幕上显示72.685 647 68°,
即锐角A ≈ 72.685 647 68°.
再按 DMs 键,将它换算成“度、分、秒”的形式,
屏幕上显示 72°41′8.33′′,
所以锐角A ≈ 72°41′8.33′′ .
例 4
利用计算器求下列各式的值:
(1) sin 20° tan 35° ;
(2) sin30°26′ = cos45°30′8′′.
在角的度量单位为“度”的状态下,
(1) sin 20° tan 35° ;
按下列顺序依次按键:
sin 20 DMS × tan 35 DMS = ,
屏幕上显示 0.239 485 082,
所以 sin 20° tan35°≈ 0.239 5;
(2) sin30°26′ = cos45°30′8′′.
按下列顺序依次按键:
1 ab/c 2 × sin 30 DMS 26 DMS + . 2 ÷ 2 ×
cos 45 DMS 30 DMS 8 DMS = ,,
屏幕上显示0.748 865 866.
所以sin30°26′+ cos45°30′8′′ ≈0.748 9.
练 习
1. 根据下列三角比的值,用计算器求相应的锐角α , β :
(1) sin α = 0.297 4;
(2) cosα = 0.785 7;
(3) tan β = .
α≈ 17°18′5″.
α≈ 38°12′52″.
β ≈ 18°26′6″.
2. 利用计算器求下列各式的值:
(1) tan 15°· cos 28° - tan 43°;
(2) cos 32°+ tan 50° + sin 40°.
≈ -0.695 9.
≈ 2.682 6.
习题 2.3
复习与巩固
1. 用计算器求下列锐角三角比的值:
(1) sin 45°, cos 35°,
tan 52°, sin 13.6° ,
cos 25.5° ;
≈ 0.707 1.
≈ 0.819 2.
≈ 1.279 9.
≈ 0.235 1.
≈ 0.902 6.
(2) sin3°12′, cos80°25′,
tan75°36′, sin56°12′10′′,
tan31°30′21′′, sin50′23′′.
≈ 0.055 8.
≈ 0.166 5.
≈ 3.894 7.
≈ 0.831 0.
≈ 0.612 9.
≈ 0.014 7.
2. 根据下列三角比的值,用计算器求相应的锐角α:
sinα=0.6; (2) sinα= 0.650 7;
(3) cosα= 0.13; (4) cosα=0.265 9;
(5) tanα=11.82; (6) tanα =0.370 5.
α≈ 36°52′12″.
α≈ 40°35′40″.
α≈ 82°31′49″.
α≈ 74°34′46″.
α≈ 85°9′51″.
α≈ 20°19′47″.
3. 利用计算器,求下列各式的值:
(1) cos 68°12′ + sin 42°- tan35°38′;
(2) .
≈ -0.058 0.
≈ -16.242 6.
拓展与延伸
4. 用计算器分别求出下列三组三角比的值:
sin 13°,cos77°;sin 62°18′,cos 27°42′;
sin 83°21′,cos 6°39′.
由此你发现了什么规律
解:sin 13°=cos 77°≈0.225 0;
sin 62°18′=cos 27°42′≈ 0.885 4;
sin 83°21'=cos 6°39′≈0.993 3.
如果 α,β 均为锐角,且α+β=90°,
那么sinα=cosβ,cosα=sinβ.
探索与创新
5. 利用本节“挑战自我”中的发现,不用计算器,比较
下列三个数的大小:
sin 62°,cos 62°, .
解:∵cos 62°-sin(90°-62°)-sin28°,
=sin 60°
且 62°>60°>28°
∴ sin 62°>sin 60°>sin 28°,
即 sin 62° > > cos 62°
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
