3.1 圆的对称性 初中数学九年级上册青岛版课件(共67张PPT)
文档属性
| 名称 | 3.1 圆的对称性 初中数学九年级上册青岛版课件(共67张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 69.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 00:00:00 | ||
图片预览











文档简介
(共67张PPT)
第3章
对圆的进一步认识
3 . 1
圆的对称性
交流与发现
你还记得什么是圆吗 你学过哪些有关圆的知识
思考下面的问题,并与同学交流:
(1) 在一张半透明的纸片上画一个圆,标出它的圆心 O,再任意作出一条直径AB将O沿直径AB折叠,你发现了什么
(2) 再任意作一条直径,重复 (1)中的操作,还有同样的结论吗
由此得到
圆是轴对称图形,每一条直径所在的直线都是它的对称轴.
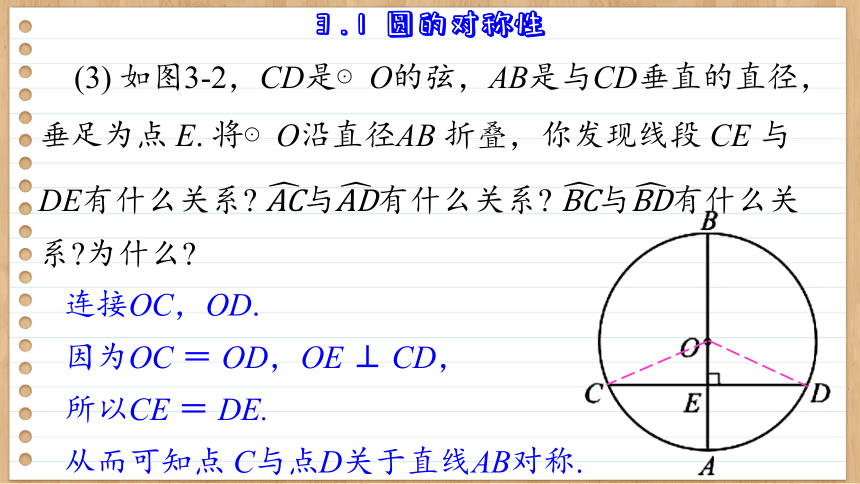
(3) 如图3-2,CD是⊙O的弦,AB是与CD垂直的直径,垂足为点 E. 将⊙O沿直径AB 折叠,你发现线段 CE 与DE有什么关系 与有什么关系 与有什么关系 为什么
连接OC,OD.
因为OC = OD,OE ⊥ CD,
所以CE = DE.
从而可知点 C与点D关于直线AB对称.
因为⊙O关于直线AB 成轴对称,
所以当⊙O沿直线AB折叠时,点 C与点D重合,与重合,与重合,
所以 =, =.
于是,便得到
*垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧.
例 1
如图3-4,以△OAB的顶点O为圆心的⊙O交AB于点 C,D,且AC=BD.
求证:OA=OB.
作OE⊥AB,垂足为点E .
E
E
由垂径定理,得 CE=DE.
∵AC=BD,
∴ AC+CE=BD+DE,
即 AE=BE.
∴ OE为线段AB的垂直平分线.
∴ OA=OB .
例 2
1400多年前,我国隋朝时期建造的赵州石拱桥的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫叫弓形的高)为7.23 m求桥拱所在圆的半径(精确到0.1 m).
解:设桥拱所在圆的半径为R(m).
如图,用表示桥拱,的圆心为O. 经过点O作弦AB的垂线,垂足为点D,与交于点C.
∵ OC ⊥ AB,
∴ D是线段AB的中点,C是
的中点,CD就是拱高.
∵ AB=37.02,CD=7.23,
∴ AD=AB=×37.02 = 18.51,
OD = OC - CD = R-7.23.
在Rt△ODA中,由勾股定理,得
OA2=AD2+OD2,
即 R2=18.512+(R-7.23)2.
解这个方程,得R≈27.3.
所以,赵州石拱桥桥拱所在圆的半径约为27.3 m.
连接OP,过点P作OP的垂线AB,交⊙O于A,B两点,则AB 就是所求作的⊙O的弦因为 OP⊥AB,根据垂径定理,得点P为AB的中点.
挑战自我
如图3-8,P为⊙O内一点,你能用尺规作⊙O的一条弦AB,使点P恰为AB的中点吗 说明你的理由.
能
练 习
1. 如图,AB是⊙O的直径,弦 CD⊥AB垂足为点M,
求证:∠ACD=∠ADC.
2. 如图,⊙O是水平放置的输油管道的横
截面,其直径为 650 mm,油面的宽度
AB=600 mm. 求油的最大深度.
F
E
解:如图,过点O作OF⊥AB 于点E,交⊙O 于点F,连接 OA,则 EF 的长就是油的最大深度.
∵OE⊥AB,
∴AE = AB = × 600 = 300(mm)
F
E
观察与思考
任意画一个圆,思考下面的问题:
(1) 如图3-1,以圆心O为旋转中心,将这个圆旋转任意一个角度,你有什么发现 特别地,如果将⊙O绕圆心旋转 180°,直径AB 的两个端点的位置会发生什么变化
(2) 圆是中心对称图形吗 如果是,哪个点是它的对称中心
圆绕着它的圆心旋转 180°,能与原来的图形重合.所以,
圆是中心对称图形,圆心是它的对称中心.
如图3-9,在⊙O上任取两点A与B,连接OA,OB,得到∠AOB.
像∠AOB 这样,顶点在圆心的角叫做圆心角 .
实验与探究
(1) 如图,任意画一个⊙O,在⊙O内画圆心角∠AOB=∠A′OB′. 连接AB,A′B′.
(2) 以点O为旋转中心,将圆心角 ∠AOB连同按逆时针方向旋转,旋转角为∠AOA′,则半径OA与OA′重合这时OB与OB′重合吗 为什么
(3) 这时,AB与A′B′重合吗 弦AB与A′B′重合吗 由此你能得到什么结论
事实上,由于∠AOA′=∠AOB+∠BOA′,
∠BOB′=∠AOB′+∠BOA′,
∠AOB =∠A′OB,
所以 ∠AOA′=∠BOB′.
由于旋转后半径OA与OA′重合,于是半径OB与OB′也重合,从而点A与A′重合,点B与B′重合.
所以与重合,弦AB与A′B′重合,即 = ,AB=A′B′.
这就是说,在同圆中,如果两个圆心角相等,那么它们所对的弧相等,所对的弦也相等.
利用旋转的基本性质还可以得出:
在同圆中,如果=,那么∠AOB=∠A′OB′,弦AB=A′B′;反之,如果弦AB =A′B′,那么∠AOB=∠A′OB′, = .
上面的结论在两个等圆中也成立.
这样,就得到下面的定理:
定理 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
例 3
如图,AB与DE是⊙O的两条直径,C是⊙O 上一点AC//DE. 求证:
(1) =;
(2) BE =EC.
(1) =;
连接OC.
∵AC//DE.
∴∠AOD=∠OAC,∠COE =∠OCA.
∵ OA=OC.
∴ ∠OAC=∠OCA.
∴ ∠AOD=∠COE.
∴ =.
(2) BE =EC.
证明:∵∠AOD =∠BOE.
∴∠BOE=∠COE.
∴ BE=CE
挑战自我
如图,在⊙O中,= 2,试判断AB与2CD的大小关系,并说明理由.
AB < 2CD.
理由如下:如图,取的中点E,连接 AE,BE.
E
E
∵=2,
∴= =.
∴AE=BE=CD.
在△AEB 中,AB<AE+BE,
∴AB<2CD.
练 习
1. 下面的说法正确吗 为什么
如图是两个同心圆,大圆的半径 OA,OB,分别交小圆于点 A′,B′. 因为∠AOB=∠A′OB′,所以 =.
解:说法不正确.
因为和不是在同圆或等圆中,虽然它们所对的圆心角相等,但是它们对应的半径不相等,因此不相等.
2. 如图,AB是⊙O的直径,AC与AD是⊙O的弦,
AC=AD. 求证:=.
3. 如图,点A,B,C,D在⊙ O上,= . AC与DB
相等吗 为什么
观察与思考
(1) 把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少
1°
(2) 把顶点在圆心的周角等分为 360 份时,整个被分成了多少份 每份的弧是否相等 为什么
360 份,相等.
在同圆中,相等的圆心角所对的弧相等.
整个圆的叫做 1°的弧. 因此,1°的圆心角所对的弧是1°的弧;反之,1°的弧所对的圆心角是1°的角.
O
1°圆心角
1°弧
一般地,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角是n°的角.
O
1°圆心角
1°弧
A
B
n°圆心角
n°弧
由此可见,圆心角与它所对的弧有以下关系:
圆心角的度数与它所对弧的度数相等.
O
1°圆心角
1°弧
A
B
n°圆心角
n°弧
例 4
如图,OA,OC是⊙O中两条垂直的半径,D是⊙O上的一点连接AD并延长与OC的延长线相交于点B,∠B=25°.求,的度数.
解:连接OD. 由已知∠AOB = 90°,∠B = 25°,
则 ∠A= 65°.
∵ OA =OD,
∴∠ODA=∠A= 65°.
于是 ∠DOA=180°- (∠ODA+∠A)
=180°- (65°+65°)
=50°.
∴ 的度数为50°.
∵ 的度数为90°,
∴ 的度数= 的度数- 的度数
= 90° - 50° = 40°.
例 5
如图3-15,在⊙O中,弦AB 所对的劣弧为圆的,圆的半径为2cm,求AB的长.
解:连接OA,OB.由题意可知, 的度数为
×360°=120°,
∴ ∠AOB = 120°.
作OC⊥AB,垂足为点C,由OA=OB,
所以∠AOC=60,AC=BC .
在Rt△AOC中,
AC=OA sin∠AOC=2· sin60°=2× = .
∴ AB=2AC=2(cm).
练 习
1. 判断下列命题是真命题还是假命题:
(1) 度数相等的弧所对的圆心角相等;
(2) 相等的圆心角所对弧的度数相等;
(3) 如果两条弧的度数相等,那么这两条弧也相等;
(4) 长度相等的弧的度数相等.
真命题
真命题
假命题
假命题
2. 如图,在⊙O中,∠B= 37°,
劣弧 的度数是多少
解:如图,连接 OA.
3. 在⊙O中,已知 的度数为120°,C为 的中点.
求证:四边形OACB是菱形.
习题 3.1
复习与巩固
1. 如图,⊙O的半径OA与弦BC垂直,
AD=2cm,BC=8cm.求⊙O的半径.
2. 如图,P是⊙O的弦BA延长线上的一点,
BA=AP=2,OP=5. 求⊙O的半径.
E
3. 如图,在⊙O中,= ,M与N分
别是OA与OB的中点. 求证:MC=NC.
4. 如图,在半径为5的⊙O中,AB,CD是
互相垂直的两条弦,垂足为点P. 已知
AB=CD=8,求OP的长.
F
E
F
E
5. ⊙O上的两点A,B将圆分成度数比为1∶3的两条弧,
且点O到AB的距离等于1. 求⊙O的半径.
6. 如图,已知AB,CD是⊙O的两条直径,弦CE//AB,
的度数为80°.求 的度数.
拓展与延伸
7. 如图,有一块半圆形木板,AB 为半圆的直径,点O为圆心.小亮要从这块木板上截出一块三角形木板,使三角形的两个顶点分别为A,B,另一个顶点在 上.怎样截才能使三角形木板的面积最大 说明你的理由.
解:当另一个顶点在的中点处时,三角形木板的面积最大.
理由如下:三角形的底边长为 AB 的长,当另一个顶点在 的中点时,三角形的高最长,所以三角形木板的面积最大
8. 如图,AB为半圆的直径,点O是圆心,E与F分别是OA,OB的中点.过点E,F作ME⊥AB,NF⊥AB,分别与半圆交于点M,N,垂足为点E,F.
求证: ==.
证明:如图,连接 OM,AM,ON.
9. 如图,在⊙O中,弦AB与弦CD相交于E点,与的度数相等.线段AE与线段DE相等吗 证明你的结论.
探索与创新
10. 如图,在⊙O中,AB与CD是两 条
弦,OE⊥AB,OF ⊥CD,垂足分
别是点E,F,OE,OF分别叫做弦
AB,CD的弦心距.
(1)已知∠AOB=∠COD,求证: OE=OF;
(2) 已知OE=OF,求证:AB=CD,
=,∠AOB=∠COD;
(3) 你能用文字语言把上述结论表述出来吗
解:结论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦的弦心距中有一组量等量,那么它们所对应的其余各组量都分别相等。
本课结束
This lesson is over
THANKS!
第3章
对圆的进一步认识
3 . 1
圆的对称性
交流与发现
你还记得什么是圆吗 你学过哪些有关圆的知识
思考下面的问题,并与同学交流:
(1) 在一张半透明的纸片上画一个圆,标出它的圆心 O,再任意作出一条直径AB将O沿直径AB折叠,你发现了什么
(2) 再任意作一条直径,重复 (1)中的操作,还有同样的结论吗
由此得到
圆是轴对称图形,每一条直径所在的直线都是它的对称轴.
(3) 如图3-2,CD是⊙O的弦,AB是与CD垂直的直径,垂足为点 E. 将⊙O沿直径AB 折叠,你发现线段 CE 与DE有什么关系 与有什么关系 与有什么关系 为什么
连接OC,OD.
因为OC = OD,OE ⊥ CD,
所以CE = DE.
从而可知点 C与点D关于直线AB对称.
因为⊙O关于直线AB 成轴对称,
所以当⊙O沿直线AB折叠时,点 C与点D重合,与重合,与重合,
所以 =, =.
于是,便得到
*垂径定理
垂直于弦的直径平分弦以及弦所对的两条弧.
例 1
如图3-4,以△OAB的顶点O为圆心的⊙O交AB于点 C,D,且AC=BD.
求证:OA=OB.
作OE⊥AB,垂足为点E .
E
E
由垂径定理,得 CE=DE.
∵AC=BD,
∴ AC+CE=BD+DE,
即 AE=BE.
∴ OE为线段AB的垂直平分线.
∴ OA=OB .
例 2
1400多年前,我国隋朝时期建造的赵州石拱桥的桥拱近似于圆弧形,它的跨度(弧所对的弦长)为37.02 m,拱高(弧的中点到弦的距离,也叫叫弓形的高)为7.23 m求桥拱所在圆的半径(精确到0.1 m).
解:设桥拱所在圆的半径为R(m).
如图,用表示桥拱,的圆心为O. 经过点O作弦AB的垂线,垂足为点D,与交于点C.
∵ OC ⊥ AB,
∴ D是线段AB的中点,C是
的中点,CD就是拱高.
∵ AB=37.02,CD=7.23,
∴ AD=AB=×37.02 = 18.51,
OD = OC - CD = R-7.23.
在Rt△ODA中,由勾股定理,得
OA2=AD2+OD2,
即 R2=18.512+(R-7.23)2.
解这个方程,得R≈27.3.
所以,赵州石拱桥桥拱所在圆的半径约为27.3 m.
连接OP,过点P作OP的垂线AB,交⊙O于A,B两点,则AB 就是所求作的⊙O的弦因为 OP⊥AB,根据垂径定理,得点P为AB的中点.
挑战自我
如图3-8,P为⊙O内一点,你能用尺规作⊙O的一条弦AB,使点P恰为AB的中点吗 说明你的理由.
能
练 习
1. 如图,AB是⊙O的直径,弦 CD⊥AB垂足为点M,
求证:∠ACD=∠ADC.
2. 如图,⊙O是水平放置的输油管道的横
截面,其直径为 650 mm,油面的宽度
AB=600 mm. 求油的最大深度.
F
E
解:如图,过点O作OF⊥AB 于点E,交⊙O 于点F,连接 OA,则 EF 的长就是油的最大深度.
∵OE⊥AB,
∴AE = AB = × 600 = 300(mm)
F
E
观察与思考
任意画一个圆,思考下面的问题:
(1) 如图3-1,以圆心O为旋转中心,将这个圆旋转任意一个角度,你有什么发现 特别地,如果将⊙O绕圆心旋转 180°,直径AB 的两个端点的位置会发生什么变化
(2) 圆是中心对称图形吗 如果是,哪个点是它的对称中心
圆绕着它的圆心旋转 180°,能与原来的图形重合.所以,
圆是中心对称图形,圆心是它的对称中心.
如图3-9,在⊙O上任取两点A与B,连接OA,OB,得到∠AOB.
像∠AOB 这样,顶点在圆心的角叫做圆心角 .
实验与探究
(1) 如图,任意画一个⊙O,在⊙O内画圆心角∠AOB=∠A′OB′. 连接AB,A′B′.
(2) 以点O为旋转中心,将圆心角 ∠AOB连同按逆时针方向旋转,旋转角为∠AOA′,则半径OA与OA′重合这时OB与OB′重合吗 为什么
(3) 这时,AB与A′B′重合吗 弦AB与A′B′重合吗 由此你能得到什么结论
事实上,由于∠AOA′=∠AOB+∠BOA′,
∠BOB′=∠AOB′+∠BOA′,
∠AOB =∠A′OB,
所以 ∠AOA′=∠BOB′.
由于旋转后半径OA与OA′重合,于是半径OB与OB′也重合,从而点A与A′重合,点B与B′重合.
所以与重合,弦AB与A′B′重合,即 = ,AB=A′B′.
这就是说,在同圆中,如果两个圆心角相等,那么它们所对的弧相等,所对的弦也相等.
利用旋转的基本性质还可以得出:
在同圆中,如果=,那么∠AOB=∠A′OB′,弦AB=A′B′;反之,如果弦AB =A′B′,那么∠AOB=∠A′OB′, = .
上面的结论在两个等圆中也成立.
这样,就得到下面的定理:
定理 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
例 3
如图,AB与DE是⊙O的两条直径,C是⊙O 上一点AC//DE. 求证:
(1) =;
(2) BE =EC.
(1) =;
连接OC.
∵AC//DE.
∴∠AOD=∠OAC,∠COE =∠OCA.
∵ OA=OC.
∴ ∠OAC=∠OCA.
∴ ∠AOD=∠COE.
∴ =.
(2) BE =EC.
证明:∵∠AOD =∠BOE.
∴∠BOE=∠COE.
∴ BE=CE
挑战自我
如图,在⊙O中,= 2,试判断AB与2CD的大小关系,并说明理由.
AB < 2CD.
理由如下:如图,取的中点E,连接 AE,BE.
E
E
∵=2,
∴= =.
∴AE=BE=CD.
在△AEB 中,AB<AE+BE,
∴AB<2CD.
练 习
1. 下面的说法正确吗 为什么
如图是两个同心圆,大圆的半径 OA,OB,分别交小圆于点 A′,B′. 因为∠AOB=∠A′OB′,所以 =.
解:说法不正确.
因为和不是在同圆或等圆中,虽然它们所对的圆心角相等,但是它们对应的半径不相等,因此不相等.
2. 如图,AB是⊙O的直径,AC与AD是⊙O的弦,
AC=AD. 求证:=.
3. 如图,点A,B,C,D在⊙ O上,= . AC与DB
相等吗 为什么
观察与思考
(1) 把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少
1°
(2) 把顶点在圆心的周角等分为 360 份时,整个被分成了多少份 每份的弧是否相等 为什么
360 份,相等.
在同圆中,相等的圆心角所对的弧相等.
整个圆的叫做 1°的弧. 因此,1°的圆心角所对的弧是1°的弧;反之,1°的弧所对的圆心角是1°的角.
O
1°圆心角
1°弧
一般地,n°的圆心角所对的弧是n°的弧;反之,n°的弧所对的圆心角是n°的角.
O
1°圆心角
1°弧
A
B
n°圆心角
n°弧
由此可见,圆心角与它所对的弧有以下关系:
圆心角的度数与它所对弧的度数相等.
O
1°圆心角
1°弧
A
B
n°圆心角
n°弧
例 4
如图,OA,OC是⊙O中两条垂直的半径,D是⊙O上的一点连接AD并延长与OC的延长线相交于点B,∠B=25°.求,的度数.
解:连接OD. 由已知∠AOB = 90°,∠B = 25°,
则 ∠A= 65°.
∵ OA =OD,
∴∠ODA=∠A= 65°.
于是 ∠DOA=180°- (∠ODA+∠A)
=180°- (65°+65°)
=50°.
∴ 的度数为50°.
∵ 的度数为90°,
∴ 的度数= 的度数- 的度数
= 90° - 50° = 40°.
例 5
如图3-15,在⊙O中,弦AB 所对的劣弧为圆的,圆的半径为2cm,求AB的长.
解:连接OA,OB.由题意可知, 的度数为
×360°=120°,
∴ ∠AOB = 120°.
作OC⊥AB,垂足为点C,由OA=OB,
所以∠AOC=60,AC=BC .
在Rt△AOC中,
AC=OA sin∠AOC=2· sin60°=2× = .
∴ AB=2AC=2(cm).
练 习
1. 判断下列命题是真命题还是假命题:
(1) 度数相等的弧所对的圆心角相等;
(2) 相等的圆心角所对弧的度数相等;
(3) 如果两条弧的度数相等,那么这两条弧也相等;
(4) 长度相等的弧的度数相等.
真命题
真命题
假命题
假命题
2. 如图,在⊙O中,∠B= 37°,
劣弧 的度数是多少
解:如图,连接 OA.
3. 在⊙O中,已知 的度数为120°,C为 的中点.
求证:四边形OACB是菱形.
习题 3.1
复习与巩固
1. 如图,⊙O的半径OA与弦BC垂直,
AD=2cm,BC=8cm.求⊙O的半径.
2. 如图,P是⊙O的弦BA延长线上的一点,
BA=AP=2,OP=5. 求⊙O的半径.
E
3. 如图,在⊙O中,= ,M与N分
别是OA与OB的中点. 求证:MC=NC.
4. 如图,在半径为5的⊙O中,AB,CD是
互相垂直的两条弦,垂足为点P. 已知
AB=CD=8,求OP的长.
F
E
F
E
5. ⊙O上的两点A,B将圆分成度数比为1∶3的两条弧,
且点O到AB的距离等于1. 求⊙O的半径.
6. 如图,已知AB,CD是⊙O的两条直径,弦CE//AB,
的度数为80°.求 的度数.
拓展与延伸
7. 如图,有一块半圆形木板,AB 为半圆的直径,点O为圆心.小亮要从这块木板上截出一块三角形木板,使三角形的两个顶点分别为A,B,另一个顶点在 上.怎样截才能使三角形木板的面积最大 说明你的理由.
解:当另一个顶点在的中点处时,三角形木板的面积最大.
理由如下:三角形的底边长为 AB 的长,当另一个顶点在 的中点时,三角形的高最长,所以三角形木板的面积最大
8. 如图,AB为半圆的直径,点O是圆心,E与F分别是OA,OB的中点.过点E,F作ME⊥AB,NF⊥AB,分别与半圆交于点M,N,垂足为点E,F.
求证: ==.
证明:如图,连接 OM,AM,ON.
9. 如图,在⊙O中,弦AB与弦CD相交于E点,与的度数相等.线段AE与线段DE相等吗 证明你的结论.
探索与创新
10. 如图,在⊙O中,AB与CD是两 条
弦,OE⊥AB,OF ⊥CD,垂足分
别是点E,F,OE,OF分别叫做弦
AB,CD的弦心距.
(1)已知∠AOB=∠COD,求证: OE=OF;
(2) 已知OE=OF,求证:AB=CD,
=,∠AOB=∠COD;
(3) 你能用文字语言把上述结论表述出来吗
解:结论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦的弦心距中有一组量等量,那么它们所对应的其余各组量都分别相等。
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
