初中数学九年级上册青岛版3.3圆周角 课件(共82张PPT)
文档属性
| 名称 | 初中数学九年级上册青岛版3.3圆周角 课件(共82张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 76.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 07:00:50 | ||
图片预览








文档简介
(共82张PPT)
第3章
对圆的进一步认识
3 . 3
圆周角
回顾旧知
请说说我们是如何给圆心角下定义的,试回答?
顶点在圆心的角叫圆心角.
A
B
O
观察与思考
(1) 如图3-22,点A,B,C是⊙O上的三个点. 以A为端点作射线AB,AC,得到了一个怎样的角
(2) (1)中的∠BAC有什么特征
∠BAC 的顶点在圆上,并且它的两边在圆内的部分是圆的两条弦,像这样的角叫做圆周角 .
(3) 圆周角与心角有什么不同
圆周角与圆心角的区别:
①顶点的位置不同:圆周角的顶点在圆上,圆心角的顶点在圆心;
②角的两边是圆的不同元素:圆周角的两边在圆内的部分都是圆的弦,圆心角的两边在圆内的部分都是圆的半径.
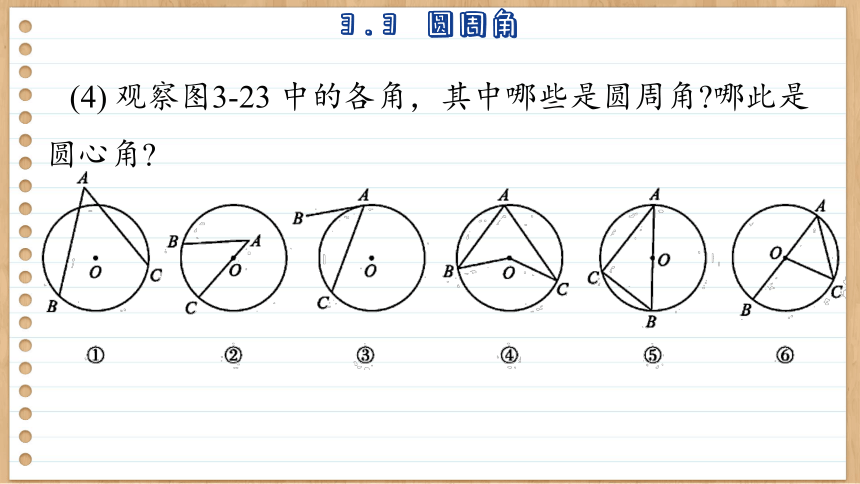
(4) 观察图3-23 中的各角,其中哪些是圆周角 哪此是圆心角
④中的∠A 是圆周角,⑤中的∠A,∠B,∠C 是圆周角,⑥中的∠A 是圆周角,④中的∠BOC 是圆心角,⑤中的∠AOB 是圆心角,⑥中的∠BOC,∠AOC,∠AOB 是圆心角.
实验与探究
任意画一个⊙O,在圆上任意取三个点A,B,C,连接AB,AC.
(1) 圆心O与∠BAC有几种可能的位置关系
与同学交流.
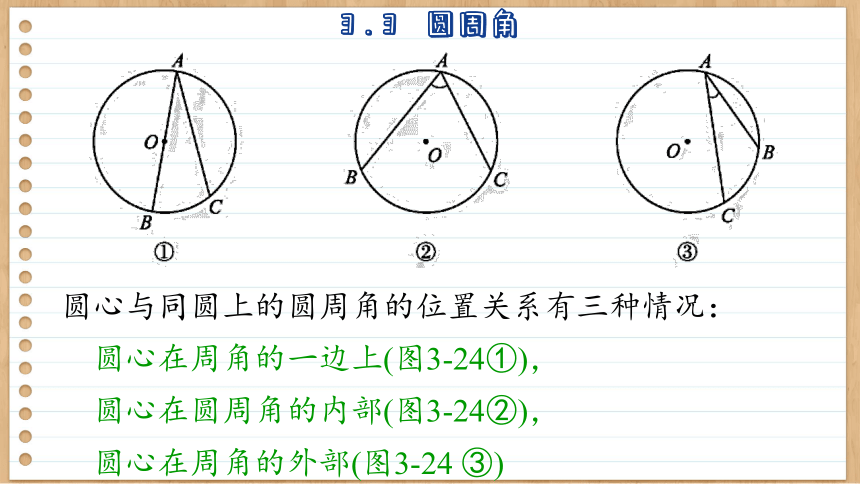
圆心与同圆上的圆周角的位置关系有三种情况:
圆心在周角的一边上(图3-24①),
圆心在圆周角的内部(图3-24②),
圆心在周角的外部(图3-24 ③)
(2) 在图3-24①中,AB是⊙O的直径,连接OC,你发现∠BOC与∠BAC有什么位置关系和数量关系
在图3-24①中∠BAC是所对的圆周角,∠BOC是所对的圆心角,同时∠BOC又是等腰三角形AOC的外角.因此可以推出,此时∠BAC=∠BOC.
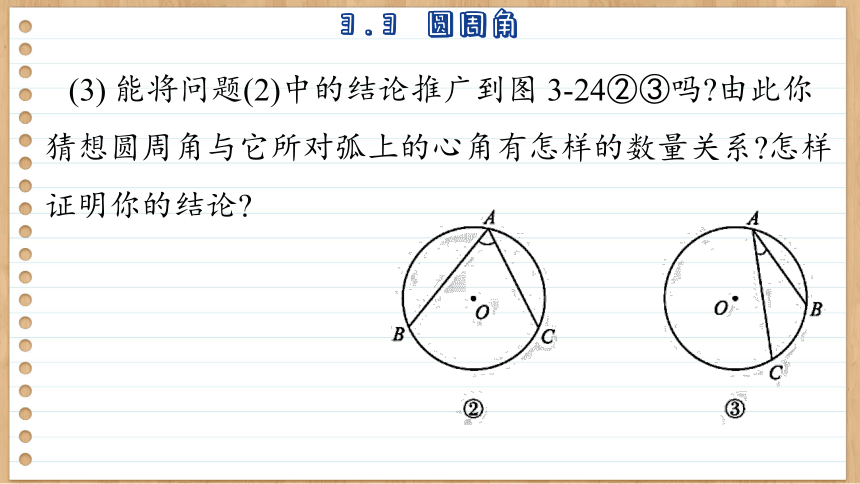
(3) 能将问题(2)中的结论推广到图 3-24②③吗 由此你猜想圆周角与它所对弧上的心角有怎样的数量关系 怎样证明你的结论
在图3-24②③中作出圆心角∠BOC及过A点的直径,可利用图3-24①中的结论,发现∠BAC与∠BOC之间有同样的关系.
已知:如图3-25,A,B,C是⊙O上的任意三点.
求证: ∠BAC=∠BOC.
证明:(1) 当圆心O在∠BAC的一条边上时(图3-25①).
在△OAB中,
∵ OA=OB,
∴ ∠BAO=∠OBA.
∵∠BOC=∠BAO+∠OBA.
∴∠BOC=2∠BAO.
∴∠BAC=∠BOC.
加油站
对于②③两种情况,通过作直径AD,原来的圆周角就转化为圆心 O在其一边上的两个圆周角的和或差,利用(1)的结论,就能推出 (2)和(3)的结论.
(2) 当圆心O在∠BAC的内部时,作直径AD(图3-25②).
由(1)的结论,得
∠BAD= ∠BOD,∠DAC = ∠DOC,
∴ ∠BAD+∠DAC= ∠BOD+ ∠DOC.
∵ ∠BAD + ∠DAC = ∠BAC,
∠BOD+ ∠DOC
= (∠BOD+∠DOC ) = ∠BOC,
∴ ∠BAC = ∠BOC.
(3) 当圆心O在∠BAC的外部时(图3-25 ③),你能给出证明吗 试一试,与同学交流.
归纳以上三种情况的结论,就得到
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
因为圆心角与它所对弧的度数相等,因而由圆周角定理可以直接得到
推论1
圆周角的度数等于它所对弧的度数的一半.
例 1
如图3-26,在⊙O中,∠AOB =110,点C在上求∠ACB的度数.
解:点C在AB的位置有两种情况:
(1) 当点 C在劣弧 AB 上时(图3-26①),
∵ ∠AOB = 110°,
∴ 的度数 =110°.
∴ 的度数=360°-110°
=250° .
∴∠ACB = × 250° = 125°.
(2) 当点C在优弧 上时(图3-26②),
∵∠AOB= 110°,
∴∠ACB = ∠AOB
= × 110°= 55°.
练 习
1. 如图,在⊙O中,∠AOB=70°,OB⊥AC,垂足为点D,求∠OBC的度数.
2. 已知△ABC内接于O,AB=AC,且的度数为130°,求∠A的度数.
观察与思考
(1) 如图3-27①,在⊙O中,∠C1,∠C2,∠C3;都是 所对的圆周角它们的大小有什么关系 由此你能得到什么结论
因为∠C1,∠C2,∠C3 的度数都等于 度数的一半,所以∠C1=∠C2=∠C3. 由此可得同弧上的圆周角相等.
(2) 如图3-27②,在⊙O中,如果 = ,那么它们所对的圆周角∠ACB与∠DFE 相等吗 反之如果 ∠ACB与∠DFE 都是⊙O的圆周角,并且∠ACB=∠DFE,那么 与 相等吗 由此你能得到什么结论 如果在等圆中呢
因为 =,∠ACB,∠DFE 的度数分别与 , 的度数的一半相等,
所以∠ACB=∠DFE,由此可得等弧上的圆周角相等,反之亦然.
于是,便得到圆周角定理的另一个推论:
推论2
同弧或等弧上的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
(3) 如图 3-28,在⊙O中,AB 是圆的直径,C是圆上异于A,B 的一点. ∠ACB的度数是多少 为什么
反过来,如果 ∠ACB是⊙O的圆周角,∠ACB= 90°,那么它所对的弦经过圆心吗 为什么
于是,得到圆周角定理的第3个推论:
推论3
直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
例 2
如图 3-29,△ABC内接于⊙O,A为劣弧的中点,∠BAC=120°.过点B作⊙O的直径BD,连接AD. 若AD=6,求AC的长.
解:∵ A是劣弧BC的中点,
∴ = .
∴ ∠ABC=∠ACB.
在△BAC中,∠BAC =120°.
∴∠ACB= (180°-120°) =30°.
∴∠D=30°.
∵ BD是⊙O的直径,
∴∠DAB =90°.
在Rt△DAB中,AD=6,
∴ AB =AD tanD = 6×=2.
∴ AC=AB =2.
例 3
如图3-30,AD是△ABC的高,AE是△ABC的外接圆直径,点O为圆心. △ADC与△ABE相似吗 说明理由
解:△ADC∽△ABE.
理由如下:
∵AE为⊙O的直径
∴∠ABE=90°.
∵AD⊥BC,
∴∠ADC=90°,∠ADC=∠ABE.
∵∠ACD =∠AEB,
∴ △ADC∽△ABE.
挑战自我
如图3-31,AB是⊙O的直径,E为⊙O上的一点,C是 的中点. CD⊥AB,垂足为点 D. AE交CD于点F,连接AC.
求证:AF=CF.
M
如图,延长 CD交 ⊙O 于点M.
M
练 习
1. 如图,在⊙O中,弦AB//CD.
(1) 与相等吗 为什么
解:相等.
∵AB//CD,∴∠5=∠1,
∴=.
(2) 你能找出图中所有相等的圆周角吗
解:∠1=∠4=∠5=∠8,
∠2=∠7,
∠3=∠6,
∠ADC=∠BCD,
∠ABC=∠BAD.
2. 某种工件有一个凹面,凹面的横截面为半圆时为合格
品. 利用一个角尺可以检验制作的工件是否合格. 下列
四种情况中,合格的工件是________,为什么
(3)
因为只有(3)符合 90°的圆周角所对的弦是直径.
观察与思考
(1) 如图3-32,四边形ABCD的顶点与⊙O具有怎样的关系
像这样,所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
在图3-32 中,四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆.
(2) ∠A与∠C是四边形ABCD 的一组对角,也都是⊙O的圆周角,它们在⊙O中所对的分别是哪两条弧 这两条弧有什么关系 从而∠A与∠C具有怎样的数量关系 ∠B与∠D也具有这样的数量关系吗
因为与的度数之和为360°,由圆周角定理可知,∠A+∠C=180°.
同理,∠B+∠D=180°.
于是,得到圆周角定理的第4个推论:
推论4
圆内接四边形的对角互补.
例 4
如图,四边形ABCD 内接于⊙O,已知∠BOD=140°,求∠C的度数.
解:∵四边形ABCD内接于⊙O.
∴∠A+∠C=180°,
∵∠BOD=140°,
∴ ∠A=∠BOD
=× 140° = 70°.
∴ ∠C=180°-∠A
=180°-70°=110°.
例 5
如图3-34,△ABC内接于⊙ O,D,F分别是 与 上的点= . 连接AF并延长交CB的延长线于点E,连接AD,CD.
求证:∠CAD = ∠E.
证明:∵ BF=DA,
∴∠BAE=∠ACD.
∴四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°.
∵∠ABC+∠ABE=180°,
∴ ∠ABE =∠D.
∴ △CDA∽△ABE.
∴∠CAD =∠E.
挑战自我
如图3-35,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,设圆心为O,延长 AD,BC 交于点E.
O
E
O
E
∵四边形ABCD是圆内接四边形,∠B=90°,
∴∠ADC=180°-∠B=90°.
∴∠CDE=90°.
∵∠A=60°,
∴∠E=30°.
O
E
在Rt△ECD 中,∠E=30°,CD=1,
∴CE=2.
在Rt△ABE 中,BE=AB·tan 60°=2,
∴BC=BE-CE=2-2.
练 习
1. 如图,四边形ABCD是⊙O的内接四边形,∠BOD= 98°,求∠A与∠C的度数.
解:∵∠A =∠BOD,∠BOD = 98°,
∴∠A = 49°.
∵∠A + ∠C = 180°,
∴∠C = 180° - 49° = 131°.
2. 如图,在圆内接四边形ABCD中,AC平分BD,并且 AC ⊥BD,∠BAD=70°,求四边形ABCD其余各角的大小.
解:∵AC 平分BD,AC⊥BD,
∴AC 是弦 BD 的垂直平分线.
∴AC是⊙O 的直径.
∴∠CBA = ∠CDA = 90°.
∵∠BAD+∠BCD=180°, ∠BAD=70°,
∴∠BCD=110°.
习题 3.3
复习与巩固
1. 如图,A,B,C是⊙O上的三个点,∠ACB=30°,
求∠BAO的度数.
2. 如图,AB,CD是⊙O的弦,延长AB,CD相交于点P.
求证: ∠P的度数等于与度数的差的一半.
3. 如图,在方格纸上有一个圆.你能用不带刻度的直尺
确定它的圆心吗 说明确定圆心的方法和理由.
解:能.
方法:作两个 90°的圆周角所对的弦,使它们交于一点,这个交点就是圆心.
理由如下:90°的圆周角所对的弦是圆的直径.
4. 如图,等边三角形ABC内接于⊙O,AD为⊙O的直径.
求∠ADB和∠CBD的度数.
5. 如图,C是⊙O的直径AB上一点,过点C作弦DE,使
CD=CO. 若的度数为40°,求的度数.
6. 如图,D是△ABC的外接圆上的一点.
AD平分△ABC的外角∠EAC,
求证:BD=CD.
拓展与延伸
7. 已知⊙O是△ABC的外接圆,且BC=, ⊙O的半
径为1,求∠A的度数.
解:分两种情况:
8. △ABC中,已知∠B= 60°,AC = 3,求△ABC的
外接圆的半径.
解:如图,连接 AO并延长交⊙O 于点B′,连接 B′C.
∵AB′是⊙O的直径,
∴∠ACB=90°
9. 如图,在⊙O中,与的中点分别为点E与F,弦
EF与AB,AC分别相交于点P,Q. 试判断△APQ的形
状,并证明你的结论.
1
2
解:△APQ 是等腰三角形.
证明如下:
连接 AE,AF,如图所示.
1
2
∵AB与AC的中点分别为点 E与F,
∴= , = .
∴∠F=∠1,∠E=∠2.
∵∠APQ=∠1+∠E,
∠AQP=∠2+∠F
∴∠APQ=∠AQP.
∴△APQ 是等腰三角形.
10. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E.点F是上的任意一点,延长AF交DC的延长线于点G,连接FC,FD.
求证:∠GFC=∠AFD.
证明:如图,连接AD.
∵AB是⊙O的直径,CD⊥AB,
∴= .
∴∠ADC=∠AFD.
∵四边形ADCF是⊙O的内接四边形,
∴∠ADC=∠GFC.
∴∠GFC=∠AFD.
探索与创新
11. 如图,BC是半圆O的直径,D,E是的三等分点,
BD,CE的延长线交于点A.
(1) 判断△ADE与△DOE的形状;
解:△ADE 与△DOE 是等边三角形.
∵D,E 是的三等分点,
∴ ==.
∴∠BOD=∠DOE=∠EOC=60°.
∵OD=OE,
∴△DOE 是等边三角形,
∴∠ODE - ∠DEO = 60°.
同理∠BDO=60°,∠CEO=60°.
∴∠ADE=∠AED=60°,
∴△ADE 是等边三角形.
(2) 如果∠A的度数不变,D,E在上移动,△ADE与
△DOE的形状是否也随之改变 说明你的理由,
解:△ADE 的形状改变,
△DOE 的形状不变.
理由如下:∵∠A=60°,
∴ D,E 在上移动时,始终有∠B +∠C = 120°.
∵∠BDO=∠B,∠CEO=∠C,
∴∠B+∠BDO+∠C+∠CEO=240°.
∵∠B+∠BDO+∠BOD+∠C+∠CEO+∠EOC=360°,
∴∠BOD+∠EOC=120°,
∴∠DOE=60°,
∴△DOE 是等边三角形.
∵∠B+∠DEC=180°,∠DEC+∠AED=180°,
∴∠AED=∠B,
同理 ∠ADE=∠C.
而∠B与∠C 都不一定为 60°,
∴ ∠AED 与∠ ADE 都不一定等于 60°,
∴△ADF 不一定是等边二角形
12. 正方形ABCD内接于⊙O.
(1) 如图,在上取一点E,连接DE,AE,BE.在DE上截取点F,使DF=BE. 在图中找出与△ADF全等的三角形,并证明你的结论.
解:△ABE≌△ADF.
证明如下:
∵四边形ABCD 是正方形,
∴AB=AD.
∵∠ABE=∠ADF,BE=DF.
∴△ABE≌△ADF(SAS)
(2) 在(1)的条件下,小莹还发现 DE,BE,AE 之间满足
下列关系:DE-BE = AE. 请你说明理由
本课结束
This lesson is over
THANKS!
第3章
对圆的进一步认识
3 . 3
圆周角
回顾旧知
请说说我们是如何给圆心角下定义的,试回答?
顶点在圆心的角叫圆心角.
A
B
O
观察与思考
(1) 如图3-22,点A,B,C是⊙O上的三个点. 以A为端点作射线AB,AC,得到了一个怎样的角
(2) (1)中的∠BAC有什么特征
∠BAC 的顶点在圆上,并且它的两边在圆内的部分是圆的两条弦,像这样的角叫做圆周角 .
(3) 圆周角与心角有什么不同
圆周角与圆心角的区别:
①顶点的位置不同:圆周角的顶点在圆上,圆心角的顶点在圆心;
②角的两边是圆的不同元素:圆周角的两边在圆内的部分都是圆的弦,圆心角的两边在圆内的部分都是圆的半径.
(4) 观察图3-23 中的各角,其中哪些是圆周角 哪此是圆心角
④中的∠A 是圆周角,⑤中的∠A,∠B,∠C 是圆周角,⑥中的∠A 是圆周角,④中的∠BOC 是圆心角,⑤中的∠AOB 是圆心角,⑥中的∠BOC,∠AOC,∠AOB 是圆心角.
实验与探究
任意画一个⊙O,在圆上任意取三个点A,B,C,连接AB,AC.
(1) 圆心O与∠BAC有几种可能的位置关系
与同学交流.
圆心与同圆上的圆周角的位置关系有三种情况:
圆心在周角的一边上(图3-24①),
圆心在圆周角的内部(图3-24②),
圆心在周角的外部(图3-24 ③)
(2) 在图3-24①中,AB是⊙O的直径,连接OC,你发现∠BOC与∠BAC有什么位置关系和数量关系
在图3-24①中∠BAC是所对的圆周角,∠BOC是所对的圆心角,同时∠BOC又是等腰三角形AOC的外角.因此可以推出,此时∠BAC=∠BOC.
(3) 能将问题(2)中的结论推广到图 3-24②③吗 由此你猜想圆周角与它所对弧上的心角有怎样的数量关系 怎样证明你的结论
在图3-24②③中作出圆心角∠BOC及过A点的直径,可利用图3-24①中的结论,发现∠BAC与∠BOC之间有同样的关系.
已知:如图3-25,A,B,C是⊙O上的任意三点.
求证: ∠BAC=∠BOC.
证明:(1) 当圆心O在∠BAC的一条边上时(图3-25①).
在△OAB中,
∵ OA=OB,
∴ ∠BAO=∠OBA.
∵∠BOC=∠BAO+∠OBA.
∴∠BOC=2∠BAO.
∴∠BAC=∠BOC.
加油站
对于②③两种情况,通过作直径AD,原来的圆周角就转化为圆心 O在其一边上的两个圆周角的和或差,利用(1)的结论,就能推出 (2)和(3)的结论.
(2) 当圆心O在∠BAC的内部时,作直径AD(图3-25②).
由(1)的结论,得
∠BAD= ∠BOD,∠DAC = ∠DOC,
∴ ∠BAD+∠DAC= ∠BOD+ ∠DOC.
∵ ∠BAD + ∠DAC = ∠BAC,
∠BOD+ ∠DOC
= (∠BOD+∠DOC ) = ∠BOC,
∴ ∠BAC = ∠BOC.
(3) 当圆心O在∠BAC的外部时(图3-25 ③),你能给出证明吗 试一试,与同学交流.
归纳以上三种情况的结论,就得到
圆周角定理 圆周角等于它所对弧上的圆心角的一半.
因为圆心角与它所对弧的度数相等,因而由圆周角定理可以直接得到
推论1
圆周角的度数等于它所对弧的度数的一半.
例 1
如图3-26,在⊙O中,∠AOB =110,点C在上求∠ACB的度数.
解:点C在AB的位置有两种情况:
(1) 当点 C在劣弧 AB 上时(图3-26①),
∵ ∠AOB = 110°,
∴ 的度数 =110°.
∴ 的度数=360°-110°
=250° .
∴∠ACB = × 250° = 125°.
(2) 当点C在优弧 上时(图3-26②),
∵∠AOB= 110°,
∴∠ACB = ∠AOB
= × 110°= 55°.
练 习
1. 如图,在⊙O中,∠AOB=70°,OB⊥AC,垂足为点D,求∠OBC的度数.
2. 已知△ABC内接于O,AB=AC,且的度数为130°,求∠A的度数.
观察与思考
(1) 如图3-27①,在⊙O中,∠C1,∠C2,∠C3;都是 所对的圆周角它们的大小有什么关系 由此你能得到什么结论
因为∠C1,∠C2,∠C3 的度数都等于 度数的一半,所以∠C1=∠C2=∠C3. 由此可得同弧上的圆周角相等.
(2) 如图3-27②,在⊙O中,如果 = ,那么它们所对的圆周角∠ACB与∠DFE 相等吗 反之如果 ∠ACB与∠DFE 都是⊙O的圆周角,并且∠ACB=∠DFE,那么 与 相等吗 由此你能得到什么结论 如果在等圆中呢
因为 =,∠ACB,∠DFE 的度数分别与 , 的度数的一半相等,
所以∠ACB=∠DFE,由此可得等弧上的圆周角相等,反之亦然.
于是,便得到圆周角定理的另一个推论:
推论2
同弧或等弧上的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧相等.
(3) 如图 3-28,在⊙O中,AB 是圆的直径,C是圆上异于A,B 的一点. ∠ACB的度数是多少 为什么
反过来,如果 ∠ACB是⊙O的圆周角,∠ACB= 90°,那么它所对的弦经过圆心吗 为什么
于是,得到圆周角定理的第3个推论:
推论3
直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
例 2
如图 3-29,△ABC内接于⊙O,A为劣弧的中点,∠BAC=120°.过点B作⊙O的直径BD,连接AD. 若AD=6,求AC的长.
解:∵ A是劣弧BC的中点,
∴ = .
∴ ∠ABC=∠ACB.
在△BAC中,∠BAC =120°.
∴∠ACB= (180°-120°) =30°.
∴∠D=30°.
∵ BD是⊙O的直径,
∴∠DAB =90°.
在Rt△DAB中,AD=6,
∴ AB =AD tanD = 6×=2.
∴ AC=AB =2.
例 3
如图3-30,AD是△ABC的高,AE是△ABC的外接圆直径,点O为圆心. △ADC与△ABE相似吗 说明理由
解:△ADC∽△ABE.
理由如下:
∵AE为⊙O的直径
∴∠ABE=90°.
∵AD⊥BC,
∴∠ADC=90°,∠ADC=∠ABE.
∵∠ACD =∠AEB,
∴ △ADC∽△ABE.
挑战自我
如图3-31,AB是⊙O的直径,E为⊙O上的一点,C是 的中点. CD⊥AB,垂足为点 D. AE交CD于点F,连接AC.
求证:AF=CF.
M
如图,延长 CD交 ⊙O 于点M.
M
练 习
1. 如图,在⊙O中,弦AB//CD.
(1) 与相等吗 为什么
解:相等.
∵AB//CD,∴∠5=∠1,
∴=.
(2) 你能找出图中所有相等的圆周角吗
解:∠1=∠4=∠5=∠8,
∠2=∠7,
∠3=∠6,
∠ADC=∠BCD,
∠ABC=∠BAD.
2. 某种工件有一个凹面,凹面的横截面为半圆时为合格
品. 利用一个角尺可以检验制作的工件是否合格. 下列
四种情况中,合格的工件是________,为什么
(3)
因为只有(3)符合 90°的圆周角所对的弦是直径.
观察与思考
(1) 如图3-32,四边形ABCD的顶点与⊙O具有怎样的关系
像这样,所有顶点都在同一个圆上的多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
在图3-32 中,四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆.
(2) ∠A与∠C是四边形ABCD 的一组对角,也都是⊙O的圆周角,它们在⊙O中所对的分别是哪两条弧 这两条弧有什么关系 从而∠A与∠C具有怎样的数量关系 ∠B与∠D也具有这样的数量关系吗
因为与的度数之和为360°,由圆周角定理可知,∠A+∠C=180°.
同理,∠B+∠D=180°.
于是,得到圆周角定理的第4个推论:
推论4
圆内接四边形的对角互补.
例 4
如图,四边形ABCD 内接于⊙O,已知∠BOD=140°,求∠C的度数.
解:∵四边形ABCD内接于⊙O.
∴∠A+∠C=180°,
∵∠BOD=140°,
∴ ∠A=∠BOD
=× 140° = 70°.
∴ ∠C=180°-∠A
=180°-70°=110°.
例 5
如图3-34,△ABC内接于⊙ O,D,F分别是 与 上的点= . 连接AF并延长交CB的延长线于点E,连接AD,CD.
求证:∠CAD = ∠E.
证明:∵ BF=DA,
∴∠BAE=∠ACD.
∴四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°.
∵∠ABC+∠ABE=180°,
∴ ∠ABE =∠D.
∴ △CDA∽△ABE.
∴∠CAD =∠E.
挑战自我
如图3-35,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,设圆心为O,延长 AD,BC 交于点E.
O
E
O
E
∵四边形ABCD是圆内接四边形,∠B=90°,
∴∠ADC=180°-∠B=90°.
∴∠CDE=90°.
∵∠A=60°,
∴∠E=30°.
O
E
在Rt△ECD 中,∠E=30°,CD=1,
∴CE=2.
在Rt△ABE 中,BE=AB·tan 60°=2,
∴BC=BE-CE=2-2.
练 习
1. 如图,四边形ABCD是⊙O的内接四边形,∠BOD= 98°,求∠A与∠C的度数.
解:∵∠A =∠BOD,∠BOD = 98°,
∴∠A = 49°.
∵∠A + ∠C = 180°,
∴∠C = 180° - 49° = 131°.
2. 如图,在圆内接四边形ABCD中,AC平分BD,并且 AC ⊥BD,∠BAD=70°,求四边形ABCD其余各角的大小.
解:∵AC 平分BD,AC⊥BD,
∴AC 是弦 BD 的垂直平分线.
∴AC是⊙O 的直径.
∴∠CBA = ∠CDA = 90°.
∵∠BAD+∠BCD=180°, ∠BAD=70°,
∴∠BCD=110°.
习题 3.3
复习与巩固
1. 如图,A,B,C是⊙O上的三个点,∠ACB=30°,
求∠BAO的度数.
2. 如图,AB,CD是⊙O的弦,延长AB,CD相交于点P.
求证: ∠P的度数等于与度数的差的一半.
3. 如图,在方格纸上有一个圆.你能用不带刻度的直尺
确定它的圆心吗 说明确定圆心的方法和理由.
解:能.
方法:作两个 90°的圆周角所对的弦,使它们交于一点,这个交点就是圆心.
理由如下:90°的圆周角所对的弦是圆的直径.
4. 如图,等边三角形ABC内接于⊙O,AD为⊙O的直径.
求∠ADB和∠CBD的度数.
5. 如图,C是⊙O的直径AB上一点,过点C作弦DE,使
CD=CO. 若的度数为40°,求的度数.
6. 如图,D是△ABC的外接圆上的一点.
AD平分△ABC的外角∠EAC,
求证:BD=CD.
拓展与延伸
7. 已知⊙O是△ABC的外接圆,且BC=, ⊙O的半
径为1,求∠A的度数.
解:分两种情况:
8. △ABC中,已知∠B= 60°,AC = 3,求△ABC的
外接圆的半径.
解:如图,连接 AO并延长交⊙O 于点B′,连接 B′C.
∵AB′是⊙O的直径,
∴∠ACB=90°
9. 如图,在⊙O中,与的中点分别为点E与F,弦
EF与AB,AC分别相交于点P,Q. 试判断△APQ的形
状,并证明你的结论.
1
2
解:△APQ 是等腰三角形.
证明如下:
连接 AE,AF,如图所示.
1
2
∵AB与AC的中点分别为点 E与F,
∴= , = .
∴∠F=∠1,∠E=∠2.
∵∠APQ=∠1+∠E,
∠AQP=∠2+∠F
∴∠APQ=∠AQP.
∴△APQ 是等腰三角形.
10. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点E.点F是上的任意一点,延长AF交DC的延长线于点G,连接FC,FD.
求证:∠GFC=∠AFD.
证明:如图,连接AD.
∵AB是⊙O的直径,CD⊥AB,
∴= .
∴∠ADC=∠AFD.
∵四边形ADCF是⊙O的内接四边形,
∴∠ADC=∠GFC.
∴∠GFC=∠AFD.
探索与创新
11. 如图,BC是半圆O的直径,D,E是的三等分点,
BD,CE的延长线交于点A.
(1) 判断△ADE与△DOE的形状;
解:△ADE 与△DOE 是等边三角形.
∵D,E 是的三等分点,
∴ ==.
∴∠BOD=∠DOE=∠EOC=60°.
∵OD=OE,
∴△DOE 是等边三角形,
∴∠ODE - ∠DEO = 60°.
同理∠BDO=60°,∠CEO=60°.
∴∠ADE=∠AED=60°,
∴△ADE 是等边三角形.
(2) 如果∠A的度数不变,D,E在上移动,△ADE与
△DOE的形状是否也随之改变 说明你的理由,
解:△ADE 的形状改变,
△DOE 的形状不变.
理由如下:∵∠A=60°,
∴ D,E 在上移动时,始终有∠B +∠C = 120°.
∵∠BDO=∠B,∠CEO=∠C,
∴∠B+∠BDO+∠C+∠CEO=240°.
∵∠B+∠BDO+∠BOD+∠C+∠CEO+∠EOC=360°,
∴∠BOD+∠EOC=120°,
∴∠DOE=60°,
∴△DOE 是等边三角形.
∵∠B+∠DEC=180°,∠DEC+∠AED=180°,
∴∠AED=∠B,
同理 ∠ADE=∠C.
而∠B与∠C 都不一定为 60°,
∴ ∠AED 与∠ ADE 都不一定等于 60°,
∴△ADF 不一定是等边二角形
12. 正方形ABCD内接于⊙O.
(1) 如图,在上取一点E,连接DE,AE,BE.在DE上截取点F,使DF=BE. 在图中找出与△ADF全等的三角形,并证明你的结论.
解:△ABE≌△ADF.
证明如下:
∵四边形ABCD 是正方形,
∴AB=AD.
∵∠ABE=∠ADF,BE=DF.
∴△ABE≌△ADF(SAS)
(2) 在(1)的条件下,小莹还发现 DE,BE,AE 之间满足
下列关系:DE-BE = AE. 请你说明理由
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
