初中数学九年级上册青岛版3.4 直线与圆的位置关系 课件(共90张PPT)
文档属性
| 名称 | 初中数学九年级上册青岛版3.4 直线与圆的位置关系 课件(共90张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 71.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 07:02:47 | ||
图片预览








文档简介
(共90张PPT)
第3章
对圆的进一步认识
3 . 4
直线与圆的位置关系
实验与探究
(1) 我们过去曾学习过点与圆的位置关系.回忆一下,在平面内一个点 P与⊙O的位置关系有几种 如果已知⊙O的半径为r,通过怎样的数量关系可以确定点P与⊙O的位置关系
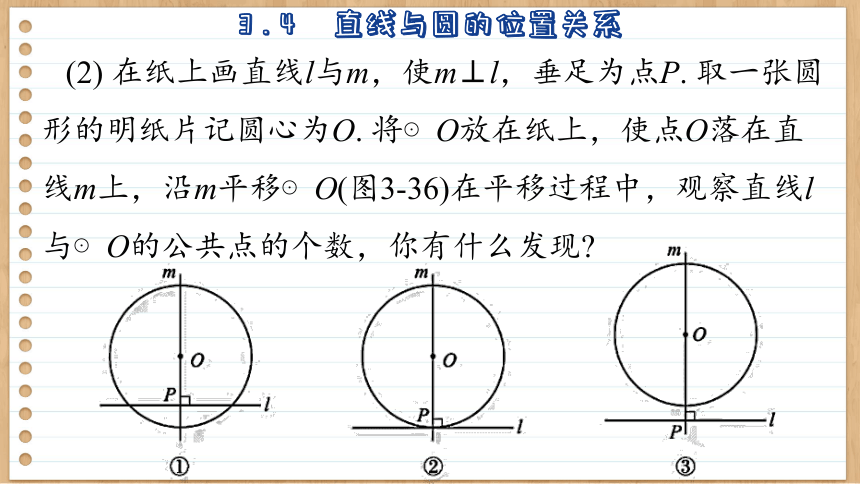
(2) 在纸上画直线l与m,使m⊥l,垂足为点P. 取一张圆形的明纸片记圆心为O. 将⊙O放在纸上,使点O落在直线m上,沿m平移⊙O(图3-36)在平移过程中,观察直线l与⊙O的公共点的个数,你有什么发现
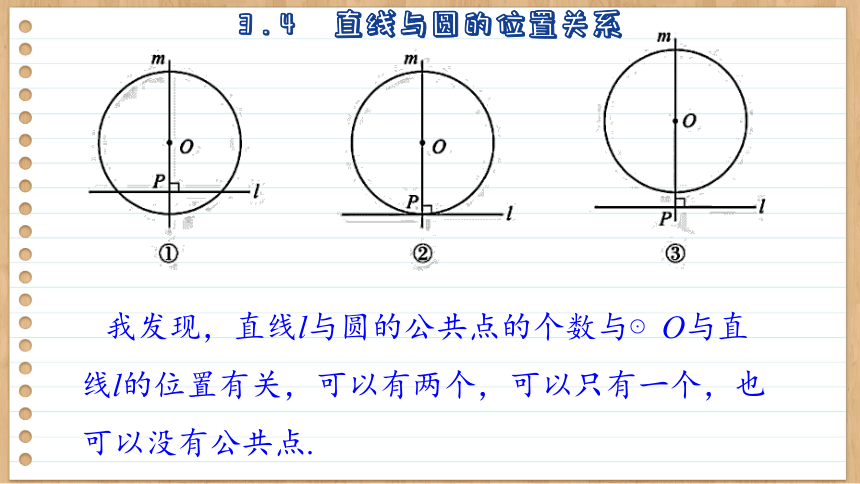
我发现,直线l与圆的公共点的个数与⊙O与直线l的位置有关,可以有两个,可以只有一个,也可以没有公共点.
当直线l与⊙O有两个公共点时(图3-36①),叫做直线l与⊙O相交. 直线l叫做⊙O的割线,两个公共点叫做交点.
当直线l与⊙O有唯一的公共点时 (图3-36②),叫做直线l与⊙O 相切.
直线l叫做⊙O的切线,唯一的公共点叫做切点.
当直线l与⊙O没有公共点时 (图3-36③),叫做直线l与⊙O相离.
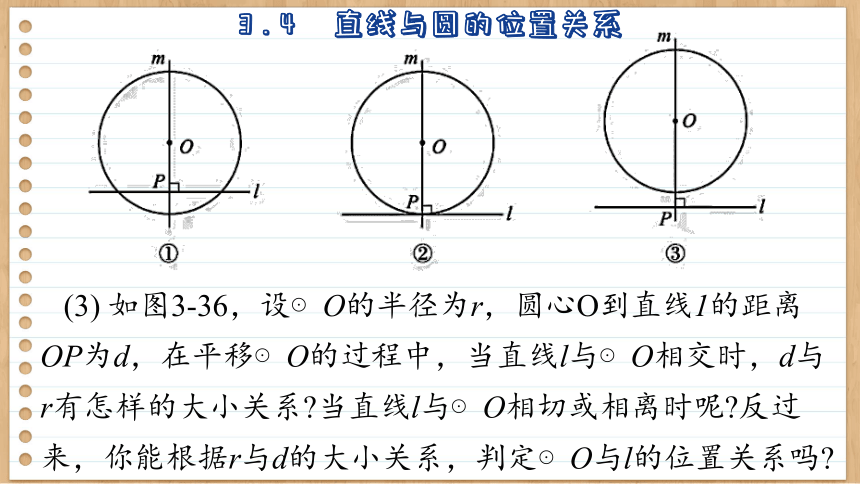
(3) 如图3-36,设⊙O的半径为r,圆心O到直线1的距离 OP为d,在平移⊙O的过程中,当直线l与⊙O相交时,d与r有怎样的大小关系 当直线l与⊙O相切或相离时呢 反过来,你能根据r与d的大小关系,判定⊙O与l的位置关系吗
当直线l与⊙O相交时,d<r;反之,当d<r 时,直线l与⊙O相交.
当直线l与⊙O相切时, ________;反之,当d=r 时,直线l与⊙O________.
当直线l与⊙O相离时,_______;反之,当d>r时,直线l与⊙O________.
d=r
相切
d>r
相离
例 1
在Rt△ABC中,∠C=90°,AC=3 cm,BC=4cm. 以点C为圆心,r为半径画圆. 当r分别取下列各值时,斜边AB 所在的直线与⊙C具有怎样的位置关系
(1) r=2 cm; (2) r=2.4 cm; (3) r=3cm .
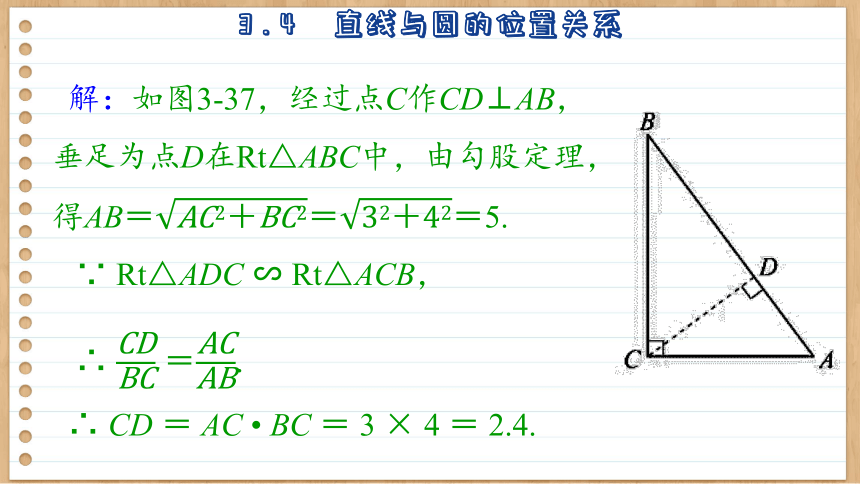
解:如图3-37,经过点C作CD⊥AB,垂足为点D在Rt△ABC中,由勾股定理,得AB===5.
∵ Rt△ADC ∽ Rt△ACB,
∴ =.
∴ CD = AC BC = 3 × 4 = 2.4.
即圆心C到AB的距离 d = 2.4 cm.
(1) 当r = 2cm时,d > r,直线AB与OC相离;
(2)当r= 2.4 cm时,d=r,直线AB与OC相切;
(3)当r=3 cm时,d < r,直线AB与OC相交.
练 习
1. 已知⊙O的半径为5 cm,点P在直线l上,若 OP=5 cm,
则直线l与⊙O有怎样的位置关系 画图说明.
相切或相交
2. 已知等腰直角三角形的直角边长为2 cm,以直角顶点
为圆心,以r为半径画圆.当r在什么范围内取值时,所
画的圆与斜边相交
观察与思考
(1) 过⊙O的半径OA的外端点A作与半径OA垂直的直线l(图3-38),你发现直线l与⊙O有怎样的位置关系 为什么
因为圆心O到直线l的距离等于⊙O的半径,所以直线l与⊙O相切.
切线的判定定理
过半径的外端并且垂直于半径的直线是圆的切线.
(2) 利用上面的定理,过⊙O 上任意一点,你会用三角尺画⊙O的切线吗 试一试
设P是⊙O上的任意一点,将三角尺的直角顶点与P点重合,一条直角边过圆心 O,再沿另外一条直角边画直线,该直线便是⊙O的经过点P的切线.
例 2
如图3-39,以△ABC的边AB 为直径作⊙O,如果⊙O经过AC的中点D,然后过D作DE⊥BC,垂足为点E. DE是⊙O的切线吗 说明理由.
解:DE是⊙O的切线.
理由如下:
连接OD.
∵AB是⊙O的直径,
∴ AO=OB.
又∵AD=DC,
∴ OD是△ABC的中位线
从而OD//BC
∵ DE⊥BC,
∴ DE⊥OD,
∴ DE是⊙O的切线.
连接OD后,把证明DE与⊙O相切转化为证明 DE⊥OD了.
在例2中,你还能由已知探索出哪些结论 说明你的理由,并与同学交流.
挑战自我
已知⊙O和圆上一点 P,你会用尺规过点 P作⊙O的切线吗 说出你的作法和作图的道理.
作法:连接 OP,过点 P作OP 的垂线l.
直线 l 就是所求作的切线.
作图的道理:过半径的外端并且垂直于半径的直线是圆的切线.
练 习
1. 如图,直线AB经过⊙O上的点 C,
并且OA=OB,CA= CB. AB是
⊙O的切线吗 为什么
解:AB 是⊙O的切线.
2. 如图,△ABC是⊙O的内接三角形,
AB为⊙O的直径,∠CAE=∠B. AE
与⊙O相切吗 为什么
你能说出切线的判定定理的逆命题吗 这个逆命题是真命题还是假命题 如果是真命题,你能给出证明吗
逆命题是“圆的切线垂直于经过切点的半径”.
不好直接证明,用反证法能行吗
已知:如图3-40,直线l与O相切于点A.
求证:OA⊥l.
证明:如图3-40,假设l与半径 OA不
垂直. 过点O作OB⊥直线l,垂足为点B.
在l上取BA′= BA,且使B点在A与A′之间,连接OA'于是OB垂直平分AA′,OA=OA′.
∵点A是切点,OA是⊙O的半径,
∴ OA′也是⊙O的半径.
这就是说,直线l与⊙O有两个公共点,即l与⊙O相交,这与已知条件“直线l与⊙O相切于点A”矛盾,所以 OA⊥l.
由此得到
切线的性质定理
圆的切线垂直于经过切点的半径.
例 3
A,B,C是⊙O上的三点,经过点A,点B分别作⊙O的切线,两切线相交于点P,如果∠P =42°,求∠ACB的度数.
(1) 如图3-41,当点C在 上时,连接OA,OB.
∵ PA,PB是⊙O的切线,A,B是切点,
∴∠OAP = ∠OBP = 90°.
在四边形OAPB中,
∵ ∠P = 42°,
∴∠AOB = 360° - ∠OAP - ∠OBP - ∠P
= 360°-90°-90°-42° = 138°.
∴ ∠ACB =∠AOB = × 138° = 69°.
在解决有关圆的切线问题时,常常需要作出过切点的半径.因为切点 A,B把⊙O分成了一条优弧和一条劣弧,所以本题应分两种情况讨论.
(2) 如图3-42,当点 C在劣弧 上时,在优弧 上任取一点 C′,连接AC′,BC′.
由(1)知,∠ACB = 69°,
在圆内接四边形ACBC′中.
∵ ∠ACB + ∠AC′B = 180°.
∴∠ACB = 180° - ∠ACB
= 180° - 69° = 111°.
练 习
1. 如图,△ABC 内接于⊙O,AB 为
直径,直线 BE切⊙O于点 B.
求证:∠A=∠CBE .
2. 如图,AB是⊙O的弦,A的延长线交过点B的⊙O的切
线于C,如果∠A=20°,求∠C的度数.
过圆上一点能画且只能画一条圆的切线,过圆外一点能画圆的几条切线
实验与探究
(1) 在透明纸上画出O,在O 上取一点 A过点A 画出⊙O的切线,在过点A的切线上任取一点 P(图3-43).
(2) 把你画出的图形沿直线 PO 对折,你发现点A关于PO的对称点 B在⊙O上吗 由此你能发现哪些结论 与同学交流.
点A关于PO的对称点B在⊙O上.连接PB,则PB与⊙O相切,点B是切点,由于PA与PB关于PO成轴对称,可以发现经过圆外一点可以画圆的两条切线PA,PB,并且PA=PB.
(3) 能证明你的结论是正确的吗
如图 3-43,已知P是⊙O外一点,PA是⊙O的切线.
过切点A作 PO的重线,垂足为点 C,交⊙O于点B,连接PB,OA,OB (图3-44 ).
图 3-43
图 3-44
图 3-44
∵ OA=OB,OP⊥AB,
∴ ∠AOP=∠BOP.
∵ OP=OP,
∴ △OPA≌ △OPB (SAS).
∵ ∠OAP=90°,
∴ ∠OBP=∠OAP=90°.
∴ PB是⊙O的切线,且PA = PB.
这就是说,经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长.
这样,就得到了
* 切线长定理
过圆外一点所画的圆的两条切线长相等.
例 4
如图3-45,P为⊙O外一点,PA,PB是⊙O的两条切线,A,B是切点,BC是⊙O的直径.
(1) 求证:AC//OP;
证明:连接OA,AB,AB交PO于点D.
∵PA,PB分别切O于A,B两点.
∴ OA=OB,PA=PB,OP =OP,△AOP≌△BOP
∴ ∠OPA=∠OPB,OP平分∠APB.
∴ PD⊥AB,∠PDA=90°
又∵BC是⊙O的直径,
∴∠CAB=90°
∴AC // OP.
(2) 如果∠APB =70°,求的度数.
∵PA=PB,
∴∠PAB =∠PBA.
∵∠APB =70°,
∴∠PBA= (180°-∠APB)
= (180° - 70°) = 55°.
∵ BC是⊙O的直径,
∴ ∠CBP = 90°.
∴∠ABC = ∠CBP - ∠PBA
= 90° - 55°=35°.
∴ 的度数= 2×∠ABC的度数
= 2 × 35°
= 70°.
挑战自我
如图 3-46①,是一个用来测量
球形物体直径的V型架,图3-46②是它抽象出的几何图形,其中PA与PB 是经过圆外一点 P的⊙O的两条切线,切点分别是A,B. ∠P =60°,如果一个乒乓球放入V型架上,量得 PA=4.5 cm,怎样求出乒乓球的直径(精确到0.1cm)
练 习
1. 如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2 cm.求∠APB的大小.
解:如图所示,连接 OA,OB.
∵PA,PB 分别切⊙O于点A,B两点,
∴OA⊥AP,OB⊥BP,OA=OB,PA=PB,OP=OP,
∴△AOP≌△BOP,
∴∠OPA=∠OPB.
设⊙O的半径为x cm,则
OP=(x+2)2cm.
由勾股定理,得 42+x2= (x+2)2,
解得x=3,
∴ OP=5 cm,
∴sin∠APO==.
∴∠APO ≈ 36.87°,
∴∠APB≈36.87°×2=73.74°.
2.如图,在直角坐标系中,OM与x轴,y轴分别相切于点A,B,已知点 B的坐标为(0,3),求点M的坐标及点M到弦AB的距离.
解:如图所示,连接 MB,MA,过点 M作MN⊥AB 于点N·
∵⊙M与轴y轴分别相切于点 A,B,
∴ ∠MBO=∠MAO=90°.
N
N
又∵∠BOA=90°,
∴四边形 AOBM 是矩形.
∵ MB=MA ,
∴矩形 AOBM 是正方形,
∴MA=MB=OB=3.
∴点M的坐标是(-3,3),∠MBA=45°.
∴点M 到弦AB的距离为MN=BM·sin45°=3×= .
习题 3.4
复习与巩固
1. 如图,⊙A的半径为2,点A (a,0) 在x轴上移动.
(1)当⊙A与y轴相离时,a的取值范围是_____________;
(2)当⊙A与y轴相切时,a的取值
是___________;
(3)当OA与y轴相交时,a的取值
范围是_____________.
a>2或a<-2
a=±2
-2< a<2
2. 如图,正方形ABCD的边长为a,AC与BD交于点E,过点E作FG//AB,分别交AD,BC于点F,G.试判断以点B为圆心,以a为半径的圆与直线AC,FG,DC 的位置关系.
3. 如图,△ABC为等腰三角形,O是底边BC的中点,
⊙O与AB相切于点D. ⊙O与AC相切吗 说明理由.
E
理由如下:如图所示,
连接 OD,过点 O作OE⊥AC 于点E.
∵△ABC 为等腰三角形,
∴∠B=∠C.
解: ⊙O与 AC 相切.
E
又∵O是BC 的中点,
∴BO=CO·
∵⊙O与AB相切于点D.
∴OD⊥AB.
又∵OE⊥AC,
∴ ∠BDO=∠CEO=90°,
∴ △BOD≌△COE,
∴OD=OE.
∴⊙O与AC 相切.
4.如图,在⊙O中,C是 的中点,过点C作直线 CD//AB.
判定CD与⊙O的位置关系,并说明理由.
解:CD与⊙O相切.
理由如下:如图所示,连接 OC.
∵C 是AB的中点,∴ OC⊥.
∵CD//AB,∴OC⊥CD,
∴ CD与⊙O相切.
5. 如图, ⊙O的半径OC= 5cm,直线l⊥OC,垂足为点
H,且l交⊙O于A,B两点AB = 8cm. 将直线l向下平移
多少时,l能与⊙O相切
解:如图所示,连接 OB.
∵ l ⊥ OC,
∴ AH = BH.
∵ AB = 8 cm,
∴ AH=BH=4 cm.
∵ OB = 5 cm,
∴ OH = = 3(cm),
∴ CH=5 - 3=2(cm),
∴ 将直线l向下平移2 cm时,
l能与⊙O相切.
6. 如图,AB是⊙O的弦,OC ⊥OA交AB于点C,过点B的直线交OC的延长线于点E. 当CE = BE时,直线BE与⊙O有怎样的位置关系 并说明你的理由.
解:直线 BE与⊙O相切.
理由如下:如图所示,连接 OB.
∵CE=BE,
∴∠EBC=∠ECB.
∵∠A+∠ACO=90°,∠ACO=∠ECB,
∴∠A+∠EBC=90°,
∴ OA=OB,
∴∠A=∠ABO,
∴∠OBE=∠ABO+∠EBC=90°,
∴ BE与⊙O相切.
7. 如图,AB为⊙O的直径,AD与⊙O相交,∠BAD的平分线交⊙O于点C,经过点C的切线交AD于点E. CE与AD垂直吗 说明理由.
解:CE与AD垂直.
如图所示,连接 OC.
∵CE与⊙O相切,
∴OC⊥EC.
∵ OC=OA,
∴∠BAC=∠ACO.
∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠DAC=∠ACO,
∴ AD//OC,
∴ CE⊥AD.
8. 如图,P是⊙O外一点,PA,PB分别与⊙O相切于点A,B,C是上任一点,过C作⊙O的切线分别交PA,PB于点D,E. 若△PDE的周长为12,求PA的长.
解:∵PA与PB是⊙O的切线,
∴PA=PB.
∴ DA,DC是⊙O的切线,
∴DA=DC.
同理,EC=EB.
∵△PDE 的周长为12,
∴PD+DC+CE+PE=12.
∴PD+DA+EB+PE=12,
即 PA+PB=12,
∴ PA=6.
拓展与延伸
9. 如图,AB是⊙O的直径,AC为⊙O的切线,BC交⊙O于点P,点Q是AC的中点. 求证:PQ是⊙O的切线.
证明:如图所示,连接 OP,AP.
∵AB 是⊙O的直径,
∴∠APB=90°,∠APC=90°.
∵Q是AC 的中点,
∴AQ=PQ,
∴∠APQ=∠PAQ.
∵OA=OP,
∴∠OPA=∠OAP.
∵AC是⊙O的切线,
∴∠BAC=90°,
∴∠OAP+∠PAQ=90°,
∴∠OPA+∠APQ=90°,
∴∠OPQ=90°,
∴PQ是⊙O的切线.
10. 如图,可以用刻度尺和一个锐角为 30°的三角尺测量计算圆形工件的直径,你能说明其中的道理吗 如果测得AB=5cm,那么圆形工件的直径是多少
C
解:如图,由刻度尺可知AB 的长度,连接 OA,OB,OC.
E
∵BA,BC与⊙O相切,
∴BA=BC.
又∵BO=BO,AO=CO,
∴△ABO≌△CBO(SSS),
∴∠ABO=∠CBO.
∵∠DBE=60°,
∴∠ABD = 120°,
C
E
∴∠ABO = 60°,
∴OA = AB · tan∠ABO = AB,
∴⊙O的直径为 2AB.
若AB= 5 cm,
则圆形工件的直径为
2×5=10(cm).
C
E
11. 如图,PC是⊙O的切线,C是切点,PO交⊙O于点A,
过点A的切线交PC干点D,CD∶DP = 1∶2,AD =
2cm.求⊙O的半径.
解:如图所示,连接 OC.
∵DC,DA 是⊙O的切线.
∴OC⊥PC,AD⊥OA,CD=AD,
∴∠DAP=∠OCP=90°.
又∵∠P=∠P,
∴ △DAP∽△OCP,
∴ =,
∴= =.
又∵AD = 2 cm,
∴CD = 2 cm ,DP = 4 cm,
∴ PC=CD+DP=6(cm).
设OC=r,则OP=2r.
在Rt△OCP 中,由勾股定理,得
OP2-OC2=PC2,
即(2r)2-r2=62,
解得 r=2 (负值舍去).
∴ ⊙O的半径是 2 cm.
12. 如图,以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于点D,DE切⊙O于点D,交BC于点E. 已知BC=10,求DE的长.
解:如图所示,连接 CD.
∵AC 是⊙O的直径,
∴∠ADC = 90°,
∴∠BDC = 90°.
∵CE ⊥ AC,
∴CE是⊙O的切线
∵ED是⊙O的切线,
∴EC=ED,
∴∠ECD=∠EDC.
∵∠ECD+∠B=90°,
∠EDC+∠EDB=90°,
∴∠B=∠EDB,
∴ED=EB,
∴EC=ED=EB.
∵BC=10,
∴DE=×10=5.
探索与创新
13. 如图,CD是⊙O的直径,直线AE切⊙O于点B,DC的延长线交AB于点A,∠A = 20°.请根据题设,写出两个你认为正确的结论,并加以证明,
答案不唯一
14. 如图,有一张紧靠墙角 (成直角 )放置的圆桌,有一把长度略小于圆的直径的刻度尺,你能用这把刻度尺测量计算这张圆桌的直径吗 请设计两种不同的方案,并说明方案的可行性.
解:方法一:测量 AB 的长度,则圆桌的直径是 2AB.
如图(1)所示,连接 OC,OB.
∵AC,AB 是⊙O的切线,
∴OC⊥AC,OB⊥AB,
∴∠ABO=∠ACO=90°.
∵∠A=90°,OC=OB,
∴四边形 ABOC 是正方形,
∴OC=AB,
∴圆桌的直径为 2OC=2AB.
方法二:测量 BC 的长度,则圆桌的直径是BC.
如图(2)所示,连接 OB,OC,BC.
∵AC,AB是⊙O的切线,
∴AB = AC,
∴∠ABC = ∠ACB.
又∵∠A = 90°,
∴∠ABC = ∠ACB = 45°.
∵sin∠ACB = ,
∴AB = BC·sin∠ACB
= BC·sin45°-BC.
∴圆的直径为2OC=2AB=2× BC
= BC.
15. 如图,在Rt△ABC中,∠C = 90°.
(1) 利用尺规按下列要求作图,并在图中标注相应字母(不写作法,保留作图痕迹 );
①作△ABC的外接圆,圆心为 O;
②以线段AC为一边,在AC的右侧作等
边三角形ACD;
③ 连接BD,交O于点E,连接AE.
略
(2) 在你作的图中,若AB=4,BC = 2.
① 判断AD与⊙O的位置关系,并证明你的结论;
② 求线段AE的长.
本课结束
This lesson is over
THANKS!
第3章
对圆的进一步认识
3 . 4
直线与圆的位置关系
实验与探究
(1) 我们过去曾学习过点与圆的位置关系.回忆一下,在平面内一个点 P与⊙O的位置关系有几种 如果已知⊙O的半径为r,通过怎样的数量关系可以确定点P与⊙O的位置关系
(2) 在纸上画直线l与m,使m⊥l,垂足为点P. 取一张圆形的明纸片记圆心为O. 将⊙O放在纸上,使点O落在直线m上,沿m平移⊙O(图3-36)在平移过程中,观察直线l与⊙O的公共点的个数,你有什么发现
我发现,直线l与圆的公共点的个数与⊙O与直线l的位置有关,可以有两个,可以只有一个,也可以没有公共点.
当直线l与⊙O有两个公共点时(图3-36①),叫做直线l与⊙O相交. 直线l叫做⊙O的割线,两个公共点叫做交点.
当直线l与⊙O有唯一的公共点时 (图3-36②),叫做直线l与⊙O 相切.
直线l叫做⊙O的切线,唯一的公共点叫做切点.
当直线l与⊙O没有公共点时 (图3-36③),叫做直线l与⊙O相离.
(3) 如图3-36,设⊙O的半径为r,圆心O到直线1的距离 OP为d,在平移⊙O的过程中,当直线l与⊙O相交时,d与r有怎样的大小关系 当直线l与⊙O相切或相离时呢 反过来,你能根据r与d的大小关系,判定⊙O与l的位置关系吗
当直线l与⊙O相交时,d<r;反之,当d<r 时,直线l与⊙O相交.
当直线l与⊙O相切时, ________;反之,当d=r 时,直线l与⊙O________.
当直线l与⊙O相离时,_______;反之,当d>r时,直线l与⊙O________.
d=r
相切
d>r
相离
例 1
在Rt△ABC中,∠C=90°,AC=3 cm,BC=4cm. 以点C为圆心,r为半径画圆. 当r分别取下列各值时,斜边AB 所在的直线与⊙C具有怎样的位置关系
(1) r=2 cm; (2) r=2.4 cm; (3) r=3cm .
解:如图3-37,经过点C作CD⊥AB,垂足为点D在Rt△ABC中,由勾股定理,得AB===5.
∵ Rt△ADC ∽ Rt△ACB,
∴ =.
∴ CD = AC BC = 3 × 4 = 2.4.
即圆心C到AB的距离 d = 2.4 cm.
(1) 当r = 2cm时,d > r,直线AB与OC相离;
(2)当r= 2.4 cm时,d=r,直线AB与OC相切;
(3)当r=3 cm时,d < r,直线AB与OC相交.
练 习
1. 已知⊙O的半径为5 cm,点P在直线l上,若 OP=5 cm,
则直线l与⊙O有怎样的位置关系 画图说明.
相切或相交
2. 已知等腰直角三角形的直角边长为2 cm,以直角顶点
为圆心,以r为半径画圆.当r在什么范围内取值时,所
画的圆与斜边相交
观察与思考
(1) 过⊙O的半径OA的外端点A作与半径OA垂直的直线l(图3-38),你发现直线l与⊙O有怎样的位置关系 为什么
因为圆心O到直线l的距离等于⊙O的半径,所以直线l与⊙O相切.
切线的判定定理
过半径的外端并且垂直于半径的直线是圆的切线.
(2) 利用上面的定理,过⊙O 上任意一点,你会用三角尺画⊙O的切线吗 试一试
设P是⊙O上的任意一点,将三角尺的直角顶点与P点重合,一条直角边过圆心 O,再沿另外一条直角边画直线,该直线便是⊙O的经过点P的切线.
例 2
如图3-39,以△ABC的边AB 为直径作⊙O,如果⊙O经过AC的中点D,然后过D作DE⊥BC,垂足为点E. DE是⊙O的切线吗 说明理由.
解:DE是⊙O的切线.
理由如下:
连接OD.
∵AB是⊙O的直径,
∴ AO=OB.
又∵AD=DC,
∴ OD是△ABC的中位线
从而OD//BC
∵ DE⊥BC,
∴ DE⊥OD,
∴ DE是⊙O的切线.
连接OD后,把证明DE与⊙O相切转化为证明 DE⊥OD了.
在例2中,你还能由已知探索出哪些结论 说明你的理由,并与同学交流.
挑战自我
已知⊙O和圆上一点 P,你会用尺规过点 P作⊙O的切线吗 说出你的作法和作图的道理.
作法:连接 OP,过点 P作OP 的垂线l.
直线 l 就是所求作的切线.
作图的道理:过半径的外端并且垂直于半径的直线是圆的切线.
练 习
1. 如图,直线AB经过⊙O上的点 C,
并且OA=OB,CA= CB. AB是
⊙O的切线吗 为什么
解:AB 是⊙O的切线.
2. 如图,△ABC是⊙O的内接三角形,
AB为⊙O的直径,∠CAE=∠B. AE
与⊙O相切吗 为什么
你能说出切线的判定定理的逆命题吗 这个逆命题是真命题还是假命题 如果是真命题,你能给出证明吗
逆命题是“圆的切线垂直于经过切点的半径”.
不好直接证明,用反证法能行吗
已知:如图3-40,直线l与O相切于点A.
求证:OA⊥l.
证明:如图3-40,假设l与半径 OA不
垂直. 过点O作OB⊥直线l,垂足为点B.
在l上取BA′= BA,且使B点在A与A′之间,连接OA'于是OB垂直平分AA′,OA=OA′.
∵点A是切点,OA是⊙O的半径,
∴ OA′也是⊙O的半径.
这就是说,直线l与⊙O有两个公共点,即l与⊙O相交,这与已知条件“直线l与⊙O相切于点A”矛盾,所以 OA⊥l.
由此得到
切线的性质定理
圆的切线垂直于经过切点的半径.
例 3
A,B,C是⊙O上的三点,经过点A,点B分别作⊙O的切线,两切线相交于点P,如果∠P =42°,求∠ACB的度数.
(1) 如图3-41,当点C在 上时,连接OA,OB.
∵ PA,PB是⊙O的切线,A,B是切点,
∴∠OAP = ∠OBP = 90°.
在四边形OAPB中,
∵ ∠P = 42°,
∴∠AOB = 360° - ∠OAP - ∠OBP - ∠P
= 360°-90°-90°-42° = 138°.
∴ ∠ACB =∠AOB = × 138° = 69°.
在解决有关圆的切线问题时,常常需要作出过切点的半径.因为切点 A,B把⊙O分成了一条优弧和一条劣弧,所以本题应分两种情况讨论.
(2) 如图3-42,当点 C在劣弧 上时,在优弧 上任取一点 C′,连接AC′,BC′.
由(1)知,∠ACB = 69°,
在圆内接四边形ACBC′中.
∵ ∠ACB + ∠AC′B = 180°.
∴∠ACB = 180° - ∠ACB
= 180° - 69° = 111°.
练 习
1. 如图,△ABC 内接于⊙O,AB 为
直径,直线 BE切⊙O于点 B.
求证:∠A=∠CBE .
2. 如图,AB是⊙O的弦,A的延长线交过点B的⊙O的切
线于C,如果∠A=20°,求∠C的度数.
过圆上一点能画且只能画一条圆的切线,过圆外一点能画圆的几条切线
实验与探究
(1) 在透明纸上画出O,在O 上取一点 A过点A 画出⊙O的切线,在过点A的切线上任取一点 P(图3-43).
(2) 把你画出的图形沿直线 PO 对折,你发现点A关于PO的对称点 B在⊙O上吗 由此你能发现哪些结论 与同学交流.
点A关于PO的对称点B在⊙O上.连接PB,则PB与⊙O相切,点B是切点,由于PA与PB关于PO成轴对称,可以发现经过圆外一点可以画圆的两条切线PA,PB,并且PA=PB.
(3) 能证明你的结论是正确的吗
如图 3-43,已知P是⊙O外一点,PA是⊙O的切线.
过切点A作 PO的重线,垂足为点 C,交⊙O于点B,连接PB,OA,OB (图3-44 ).
图 3-43
图 3-44
图 3-44
∵ OA=OB,OP⊥AB,
∴ ∠AOP=∠BOP.
∵ OP=OP,
∴ △OPA≌ △OPB (SAS).
∵ ∠OAP=90°,
∴ ∠OBP=∠OAP=90°.
∴ PB是⊙O的切线,且PA = PB.
这就是说,经过圆外一点可以画圆的两条切线,这点与其中一个切点之间的线段的长,叫做这点到圆的切线长.
这样,就得到了
* 切线长定理
过圆外一点所画的圆的两条切线长相等.
例 4
如图3-45,P为⊙O外一点,PA,PB是⊙O的两条切线,A,B是切点,BC是⊙O的直径.
(1) 求证:AC//OP;
证明:连接OA,AB,AB交PO于点D.
∵PA,PB分别切O于A,B两点.
∴ OA=OB,PA=PB,OP =OP,△AOP≌△BOP
∴ ∠OPA=∠OPB,OP平分∠APB.
∴ PD⊥AB,∠PDA=90°
又∵BC是⊙O的直径,
∴∠CAB=90°
∴AC // OP.
(2) 如果∠APB =70°,求的度数.
∵PA=PB,
∴∠PAB =∠PBA.
∵∠APB =70°,
∴∠PBA= (180°-∠APB)
= (180° - 70°) = 55°.
∵ BC是⊙O的直径,
∴ ∠CBP = 90°.
∴∠ABC = ∠CBP - ∠PBA
= 90° - 55°=35°.
∴ 的度数= 2×∠ABC的度数
= 2 × 35°
= 70°.
挑战自我
如图 3-46①,是一个用来测量
球形物体直径的V型架,图3-46②是它抽象出的几何图形,其中PA与PB 是经过圆外一点 P的⊙O的两条切线,切点分别是A,B. ∠P =60°,如果一个乒乓球放入V型架上,量得 PA=4.5 cm,怎样求出乒乓球的直径(精确到0.1cm)
练 习
1. 如图,P是⊙O外一点,PA,PB是⊙O的两条切线,A,B为切点,OP交⊙O于点C,PA=4cm,PC=2 cm.求∠APB的大小.
解:如图所示,连接 OA,OB.
∵PA,PB 分别切⊙O于点A,B两点,
∴OA⊥AP,OB⊥BP,OA=OB,PA=PB,OP=OP,
∴△AOP≌△BOP,
∴∠OPA=∠OPB.
设⊙O的半径为x cm,则
OP=(x+2)2cm.
由勾股定理,得 42+x2= (x+2)2,
解得x=3,
∴ OP=5 cm,
∴sin∠APO==.
∴∠APO ≈ 36.87°,
∴∠APB≈36.87°×2=73.74°.
2.如图,在直角坐标系中,OM与x轴,y轴分别相切于点A,B,已知点 B的坐标为(0,3),求点M的坐标及点M到弦AB的距离.
解:如图所示,连接 MB,MA,过点 M作MN⊥AB 于点N·
∵⊙M与轴y轴分别相切于点 A,B,
∴ ∠MBO=∠MAO=90°.
N
N
又∵∠BOA=90°,
∴四边形 AOBM 是矩形.
∵ MB=MA ,
∴矩形 AOBM 是正方形,
∴MA=MB=OB=3.
∴点M的坐标是(-3,3),∠MBA=45°.
∴点M 到弦AB的距离为MN=BM·sin45°=3×= .
习题 3.4
复习与巩固
1. 如图,⊙A的半径为2,点A (a,0) 在x轴上移动.
(1)当⊙A与y轴相离时,a的取值范围是_____________;
(2)当⊙A与y轴相切时,a的取值
是___________;
(3)当OA与y轴相交时,a的取值
范围是_____________.
a>2或a<-2
a=±2
-2< a<2
2. 如图,正方形ABCD的边长为a,AC与BD交于点E,过点E作FG//AB,分别交AD,BC于点F,G.试判断以点B为圆心,以a为半径的圆与直线AC,FG,DC 的位置关系.
3. 如图,△ABC为等腰三角形,O是底边BC的中点,
⊙O与AB相切于点D. ⊙O与AC相切吗 说明理由.
E
理由如下:如图所示,
连接 OD,过点 O作OE⊥AC 于点E.
∵△ABC 为等腰三角形,
∴∠B=∠C.
解: ⊙O与 AC 相切.
E
又∵O是BC 的中点,
∴BO=CO·
∵⊙O与AB相切于点D.
∴OD⊥AB.
又∵OE⊥AC,
∴ ∠BDO=∠CEO=90°,
∴ △BOD≌△COE,
∴OD=OE.
∴⊙O与AC 相切.
4.如图,在⊙O中,C是 的中点,过点C作直线 CD//AB.
判定CD与⊙O的位置关系,并说明理由.
解:CD与⊙O相切.
理由如下:如图所示,连接 OC.
∵C 是AB的中点,∴ OC⊥.
∵CD//AB,∴OC⊥CD,
∴ CD与⊙O相切.
5. 如图, ⊙O的半径OC= 5cm,直线l⊥OC,垂足为点
H,且l交⊙O于A,B两点AB = 8cm. 将直线l向下平移
多少时,l能与⊙O相切
解:如图所示,连接 OB.
∵ l ⊥ OC,
∴ AH = BH.
∵ AB = 8 cm,
∴ AH=BH=4 cm.
∵ OB = 5 cm,
∴ OH = = 3(cm),
∴ CH=5 - 3=2(cm),
∴ 将直线l向下平移2 cm时,
l能与⊙O相切.
6. 如图,AB是⊙O的弦,OC ⊥OA交AB于点C,过点B的直线交OC的延长线于点E. 当CE = BE时,直线BE与⊙O有怎样的位置关系 并说明你的理由.
解:直线 BE与⊙O相切.
理由如下:如图所示,连接 OB.
∵CE=BE,
∴∠EBC=∠ECB.
∵∠A+∠ACO=90°,∠ACO=∠ECB,
∴∠A+∠EBC=90°,
∴ OA=OB,
∴∠A=∠ABO,
∴∠OBE=∠ABO+∠EBC=90°,
∴ BE与⊙O相切.
7. 如图,AB为⊙O的直径,AD与⊙O相交,∠BAD的平分线交⊙O于点C,经过点C的切线交AD于点E. CE与AD垂直吗 说明理由.
解:CE与AD垂直.
如图所示,连接 OC.
∵CE与⊙O相切,
∴OC⊥EC.
∵ OC=OA,
∴∠BAC=∠ACO.
∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠DAC=∠ACO,
∴ AD//OC,
∴ CE⊥AD.
8. 如图,P是⊙O外一点,PA,PB分别与⊙O相切于点A,B,C是上任一点,过C作⊙O的切线分别交PA,PB于点D,E. 若△PDE的周长为12,求PA的长.
解:∵PA与PB是⊙O的切线,
∴PA=PB.
∴ DA,DC是⊙O的切线,
∴DA=DC.
同理,EC=EB.
∵△PDE 的周长为12,
∴PD+DC+CE+PE=12.
∴PD+DA+EB+PE=12,
即 PA+PB=12,
∴ PA=6.
拓展与延伸
9. 如图,AB是⊙O的直径,AC为⊙O的切线,BC交⊙O于点P,点Q是AC的中点. 求证:PQ是⊙O的切线.
证明:如图所示,连接 OP,AP.
∵AB 是⊙O的直径,
∴∠APB=90°,∠APC=90°.
∵Q是AC 的中点,
∴AQ=PQ,
∴∠APQ=∠PAQ.
∵OA=OP,
∴∠OPA=∠OAP.
∵AC是⊙O的切线,
∴∠BAC=90°,
∴∠OAP+∠PAQ=90°,
∴∠OPA+∠APQ=90°,
∴∠OPQ=90°,
∴PQ是⊙O的切线.
10. 如图,可以用刻度尺和一个锐角为 30°的三角尺测量计算圆形工件的直径,你能说明其中的道理吗 如果测得AB=5cm,那么圆形工件的直径是多少
C
解:如图,由刻度尺可知AB 的长度,连接 OA,OB,OC.
E
∵BA,BC与⊙O相切,
∴BA=BC.
又∵BO=BO,AO=CO,
∴△ABO≌△CBO(SSS),
∴∠ABO=∠CBO.
∵∠DBE=60°,
∴∠ABD = 120°,
C
E
∴∠ABO = 60°,
∴OA = AB · tan∠ABO = AB,
∴⊙O的直径为 2AB.
若AB= 5 cm,
则圆形工件的直径为
2×5=10(cm).
C
E
11. 如图,PC是⊙O的切线,C是切点,PO交⊙O于点A,
过点A的切线交PC干点D,CD∶DP = 1∶2,AD =
2cm.求⊙O的半径.
解:如图所示,连接 OC.
∵DC,DA 是⊙O的切线.
∴OC⊥PC,AD⊥OA,CD=AD,
∴∠DAP=∠OCP=90°.
又∵∠P=∠P,
∴ △DAP∽△OCP,
∴ =,
∴= =.
又∵AD = 2 cm,
∴CD = 2 cm ,DP = 4 cm,
∴ PC=CD+DP=6(cm).
设OC=r,则OP=2r.
在Rt△OCP 中,由勾股定理,得
OP2-OC2=PC2,
即(2r)2-r2=62,
解得 r=2 (负值舍去).
∴ ⊙O的半径是 2 cm.
12. 如图,以Rt△ABC的直角边AC为直径作⊙O,交斜边AB于点D,DE切⊙O于点D,交BC于点E. 已知BC=10,求DE的长.
解:如图所示,连接 CD.
∵AC 是⊙O的直径,
∴∠ADC = 90°,
∴∠BDC = 90°.
∵CE ⊥ AC,
∴CE是⊙O的切线
∵ED是⊙O的切线,
∴EC=ED,
∴∠ECD=∠EDC.
∵∠ECD+∠B=90°,
∠EDC+∠EDB=90°,
∴∠B=∠EDB,
∴ED=EB,
∴EC=ED=EB.
∵BC=10,
∴DE=×10=5.
探索与创新
13. 如图,CD是⊙O的直径,直线AE切⊙O于点B,DC的延长线交AB于点A,∠A = 20°.请根据题设,写出两个你认为正确的结论,并加以证明,
答案不唯一
14. 如图,有一张紧靠墙角 (成直角 )放置的圆桌,有一把长度略小于圆的直径的刻度尺,你能用这把刻度尺测量计算这张圆桌的直径吗 请设计两种不同的方案,并说明方案的可行性.
解:方法一:测量 AB 的长度,则圆桌的直径是 2AB.
如图(1)所示,连接 OC,OB.
∵AC,AB 是⊙O的切线,
∴OC⊥AC,OB⊥AB,
∴∠ABO=∠ACO=90°.
∵∠A=90°,OC=OB,
∴四边形 ABOC 是正方形,
∴OC=AB,
∴圆桌的直径为 2OC=2AB.
方法二:测量 BC 的长度,则圆桌的直径是BC.
如图(2)所示,连接 OB,OC,BC.
∵AC,AB是⊙O的切线,
∴AB = AC,
∴∠ABC = ∠ACB.
又∵∠A = 90°,
∴∠ABC = ∠ACB = 45°.
∵sin∠ACB = ,
∴AB = BC·sin∠ACB
= BC·sin45°-BC.
∴圆的直径为2OC=2AB=2× BC
= BC.
15. 如图,在Rt△ABC中,∠C = 90°.
(1) 利用尺规按下列要求作图,并在图中标注相应字母(不写作法,保留作图痕迹 );
①作△ABC的外接圆,圆心为 O;
②以线段AC为一边,在AC的右侧作等
边三角形ACD;
③ 连接BD,交O于点E,连接AE.
略
(2) 在你作的图中,若AB=4,BC = 2.
① 判断AD与⊙O的位置关系,并证明你的结论;
② 求线段AE的长.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
