初中数学九年级上册青岛版3.6 弧长及扇形面积的计算 课件(共40张PPT)
文档属性
| 名称 | 初中数学九年级上册青岛版3.6 弧长及扇形面积的计算 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 67.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 07:06:07 | ||
图片预览











文档简介
(共40张PPT)
第3章
对圆的进一步认识
3 . 6
弧长及扇形面积的计算
学习目标
1. 经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.
2. 了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.
新课导入
在生产和生活实际中,有时需要求一段弧的长度或一个扇形的面积.
我们过去学习过圆的周长公式和面积公式,怎样利用这两个公式分别推导出弧长及扇形的面积的计算公式呢
交流与发现
已知圆的半径为r. 思考下面的问题:
(1) 圆周上1°弧的长度是整个圆周长的多少 怎样用圆的半径r表示1°弧的长度呢
,
1°的圆心角所对的弧长为,即.
(2) 由(1),怎样用圆的半径r表示 n°弧的长度l呢
与同学交流
l=.
(3) 在⊙O中,圆心角为1°的扇形的面积是整个圆面积的多少 怎样用圆的半径下表示圆心角为1°的扇形的面积呢
,
圆心角是1°的扇形面积.
(4) 由 (3),怎样用的半径r表示圆心角为n°的扇形面积S形呢
S扇形=.
(5) 如果已知⊙O的半径r和扇形的弧长l,怎样用l与r表示这段弧所在的扇形的面积呢
因为扇形的弧长 l=,所以 =lr .于是
S扇形=.
例 1
如图3-50 所示为一段弯形管道,其中心线是一段圆弧 AB 已知AB 的圆心为O,半径OA = 60 cm,∠AOB=108°,求这段弯管的长度(精确到0.1 cm ).
解:由图3-50可知,n=108°,r=60 cm,代入弧长公式,得
l== ≈113.1 (cm)
所以,这段弯管的长度约为113.1 cm.
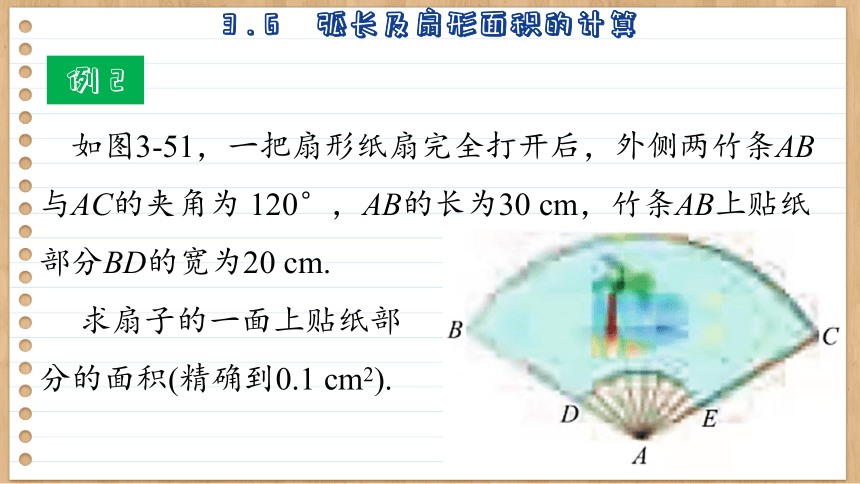
例 2
如图3-51,一把扇形纸扇完全打开后,外侧两竹条AB与AC的夹角为 120°,AB的长为30 cm,竹条AB上贴纸部分BD的宽为20 cm.
求扇子的一面上贴纸部
分的面积(精确到0.1 cm2).
解:由图3-51可知,扇形的圆心为A,圆心角n=120°,AB=30 cm,BD=20 cm,图上贴纸部分的面积等于两个扇形面积的差.由扇形的面积公式,贴纸部分的面积为
S扇形BAC-S扇形DAE
=-
= -
=π( 302 - 102) ≈837.8 (cm2)
所以,扇子的一面上贴纸部分的面积约为837.8 cm2.
挑战自我
已知扇形AOB的半径为r,∠AOB=90°,以弦AB为直径作半圆,得到图 3-52. 你会求图中“新月形”(阴影部分)的面积吗 试一试.
会
智趣园
计算花瓶形的面积
4个半径为1 cm 的等圆的位置如图 3-53 所示,其中阴影部分酷似一个花瓶的纵断面(不妨称其为花瓶形 ).你会计算这个花瓶形的面积吗
方法一:将图3-54左图的花瓶形沿图中的虚线剪成四块,可以拼成右图的正方形.
因此,所求的花瓶形的面积等于所拼成的正方形的面积.因为正方形的边长等于等圆的半径的2倍,即2cm,所以这个花瓶形的面积为2×2=4(cm2).
方法二:将图3-55 左图中的花瓶形沿图中的虚线剪成4块,也可以拼成右图的正方形,你能说出这时正方形的边长2是怎样求出的吗
方法三:将图3-56 左图的花瓶形沿图中的虚线剪成 3块,也能拼成右图的正方形,想一想,这时正方形的边长是怎样算出的
图 3-57 是另外一种计算方法的示意图,请按照图示求出花瓶形的面积.
除了上述四种方法外,你还能想出求花瓶形面积的其他方法吗
练 习
1. 如图,桥拱的形状是一段圆弧,桥拱 的度数是
90°,半径 OA为 30 m.
求桥拱 的长(精确到0.1m).
2. 如图,水平放置的排水管的横截面为圆形,圆的半径为10 cm水面宽度AB为 10 cm. 求截面中有水部分的面积(精确到0.1 cm2).
习题 3.6
复习与巩固
1. 如图,公路的拐弯处有一段弯道是圆弧形,道路长 12 m,孤所对的圆心角是 81°.求这段弧的半径r (精确到 0.1 m).
2. 扇形的弧长为3π cm,半径为8 cm. 求该扇形的面积.
3. 在矩形ABCD中,AB=1,BC=. 以BC的中点E为圆
心画弧与AD相切,切点为P,点M,N分别在AB
与CD上. 求扇形EMN的面积.
4. 如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径. 设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积. 请你说出小亮是如何算出来的.
解:如图所示,过点O作OE⊥AB 于点E,连接OA则AE=AB = .
E
设大圆的半径为 R,小圆的半径为 r.
在Rt△AOE中, OA2 = AE2 + OE2,
∵ OA = R,OE = r,AE = ,
∴ R2=()2+r2,
∴ R2- r2 = ()2 - .
故剩余部分的面积为 πR2- πr2 = (R2-r2)
=× = .
E
5. 如图,正方形的边长为a,分别以各边为直径在正方形内画半圆. 求阴影部分的面积.
拓展与延伸
解:如图所示,O为AC 的中点,
连接 AB,BO,
A
B
O
C
A
B
O
C
6. 如图,大圆⊙O的半径OA是小圆⊙O1,的直径,⊙O
的半径OC交⊙O1,于点B. 求证:与的长相等.
探索与创新
7. 如图,ABCD是边长为1的正方形,其中,,
的圆心依次是A,B,C .
(1) 求点D沿三条圆弧运动到
点 G所经过的路线长;
(2) 求图中阴影部分的面积.
本课结束
This lesson is over
THANKS!
第3章
对圆的进一步认识
3 . 6
弧长及扇形面积的计算
学习目标
1. 经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.
2. 了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.
新课导入
在生产和生活实际中,有时需要求一段弧的长度或一个扇形的面积.
我们过去学习过圆的周长公式和面积公式,怎样利用这两个公式分别推导出弧长及扇形的面积的计算公式呢
交流与发现
已知圆的半径为r. 思考下面的问题:
(1) 圆周上1°弧的长度是整个圆周长的多少 怎样用圆的半径r表示1°弧的长度呢
,
1°的圆心角所对的弧长为,即.
(2) 由(1),怎样用圆的半径r表示 n°弧的长度l呢
与同学交流
l=.
(3) 在⊙O中,圆心角为1°的扇形的面积是整个圆面积的多少 怎样用圆的半径下表示圆心角为1°的扇形的面积呢
,
圆心角是1°的扇形面积.
(4) 由 (3),怎样用的半径r表示圆心角为n°的扇形面积S形呢
S扇形=.
(5) 如果已知⊙O的半径r和扇形的弧长l,怎样用l与r表示这段弧所在的扇形的面积呢
因为扇形的弧长 l=,所以 =lr .于是
S扇形=.
例 1
如图3-50 所示为一段弯形管道,其中心线是一段圆弧 AB 已知AB 的圆心为O,半径OA = 60 cm,∠AOB=108°,求这段弯管的长度(精确到0.1 cm ).
解:由图3-50可知,n=108°,r=60 cm,代入弧长公式,得
l== ≈113.1 (cm)
所以,这段弯管的长度约为113.1 cm.
例 2
如图3-51,一把扇形纸扇完全打开后,外侧两竹条AB与AC的夹角为 120°,AB的长为30 cm,竹条AB上贴纸部分BD的宽为20 cm.
求扇子的一面上贴纸部
分的面积(精确到0.1 cm2).
解:由图3-51可知,扇形的圆心为A,圆心角n=120°,AB=30 cm,BD=20 cm,图上贴纸部分的面积等于两个扇形面积的差.由扇形的面积公式,贴纸部分的面积为
S扇形BAC-S扇形DAE
=-
= -
=π( 302 - 102) ≈837.8 (cm2)
所以,扇子的一面上贴纸部分的面积约为837.8 cm2.
挑战自我
已知扇形AOB的半径为r,∠AOB=90°,以弦AB为直径作半圆,得到图 3-52. 你会求图中“新月形”(阴影部分)的面积吗 试一试.
会
智趣园
计算花瓶形的面积
4个半径为1 cm 的等圆的位置如图 3-53 所示,其中阴影部分酷似一个花瓶的纵断面(不妨称其为花瓶形 ).你会计算这个花瓶形的面积吗
方法一:将图3-54左图的花瓶形沿图中的虚线剪成四块,可以拼成右图的正方形.
因此,所求的花瓶形的面积等于所拼成的正方形的面积.因为正方形的边长等于等圆的半径的2倍,即2cm,所以这个花瓶形的面积为2×2=4(cm2).
方法二:将图3-55 左图中的花瓶形沿图中的虚线剪成4块,也可以拼成右图的正方形,你能说出这时正方形的边长2是怎样求出的吗
方法三:将图3-56 左图的花瓶形沿图中的虚线剪成 3块,也能拼成右图的正方形,想一想,这时正方形的边长是怎样算出的
图 3-57 是另外一种计算方法的示意图,请按照图示求出花瓶形的面积.
除了上述四种方法外,你还能想出求花瓶形面积的其他方法吗
练 习
1. 如图,桥拱的形状是一段圆弧,桥拱 的度数是
90°,半径 OA为 30 m.
求桥拱 的长(精确到0.1m).
2. 如图,水平放置的排水管的横截面为圆形,圆的半径为10 cm水面宽度AB为 10 cm. 求截面中有水部分的面积(精确到0.1 cm2).
习题 3.6
复习与巩固
1. 如图,公路的拐弯处有一段弯道是圆弧形,道路长 12 m,孤所对的圆心角是 81°.求这段弧的半径r (精确到 0.1 m).
2. 扇形的弧长为3π cm,半径为8 cm. 求该扇形的面积.
3. 在矩形ABCD中,AB=1,BC=. 以BC的中点E为圆
心画弧与AD相切,切点为P,点M,N分别在AB
与CD上. 求扇形EMN的面积.
4. 如图,从一张半圆形的铁片上剪下了一个小的半圆形铁片,为了计算剩余部分的面积,小亮在图中作出一条小圆的切线,并使它平行于大圆的直径. 设这条切线交大圆于点A,B,量得AB的长是a,便可求出剩余部分的面积. 请你说出小亮是如何算出来的.
解:如图所示,过点O作OE⊥AB 于点E,连接OA则AE=AB = .
E
设大圆的半径为 R,小圆的半径为 r.
在Rt△AOE中, OA2 = AE2 + OE2,
∵ OA = R,OE = r,AE = ,
∴ R2=()2+r2,
∴ R2- r2 = ()2 - .
故剩余部分的面积为 πR2- πr2 = (R2-r2)
=× = .
E
5. 如图,正方形的边长为a,分别以各边为直径在正方形内画半圆. 求阴影部分的面积.
拓展与延伸
解:如图所示,O为AC 的中点,
连接 AB,BO,
A
B
O
C
A
B
O
C
6. 如图,大圆⊙O的半径OA是小圆⊙O1,的直径,⊙O
的半径OC交⊙O1,于点B. 求证:与的长相等.
探索与创新
7. 如图,ABCD是边长为1的正方形,其中,,
的圆心依次是A,B,C .
(1) 求点D沿三条圆弧运动到
点 G所经过的路线长;
(2) 求图中阴影部分的面积.
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
