初中数学九年级上册青岛版4.7 一元二次方程的应用 课件(共45张PPT)
文档属性
| 名称 | 初中数学九年级上册青岛版4.7 一元二次方程的应用 课件(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 61.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 09:23:04 | ||
图片预览









文档简介
(共45张PPT)
第4章
一元二次方程
4 . 7
一元二次方程的应用
学习目标
1. 使学生会用列一元二次方程的方法解有关面积、体
积方面的应用问题.
2. 进一步培养学生化实际问题为数学问题的能力和分
析问题解决问题的能力,培养用数学的意识.
交流与发现
与我们学过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活与生产中数量关系的有效模型.
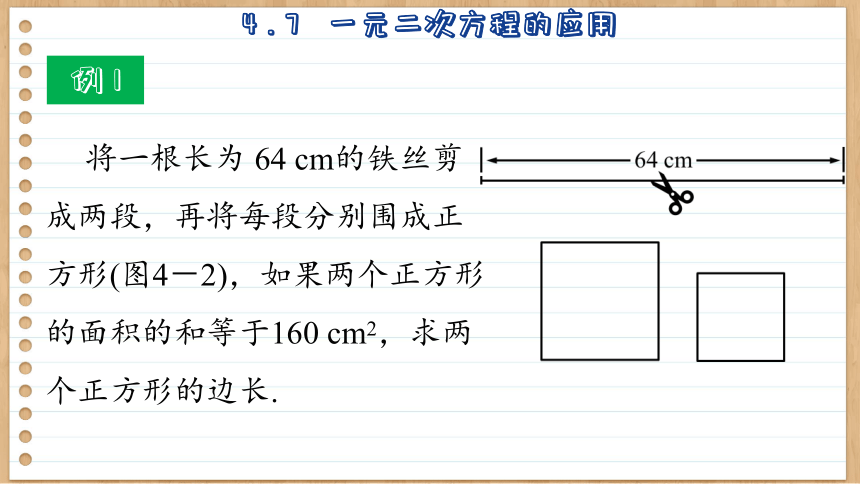
例 1
将一根长为 64 cm的铁丝剪成两段,再将每段分别围成正方形(图4-2),如果两个正方形的面积的和等于160 cm2,求两个正方形的边长.
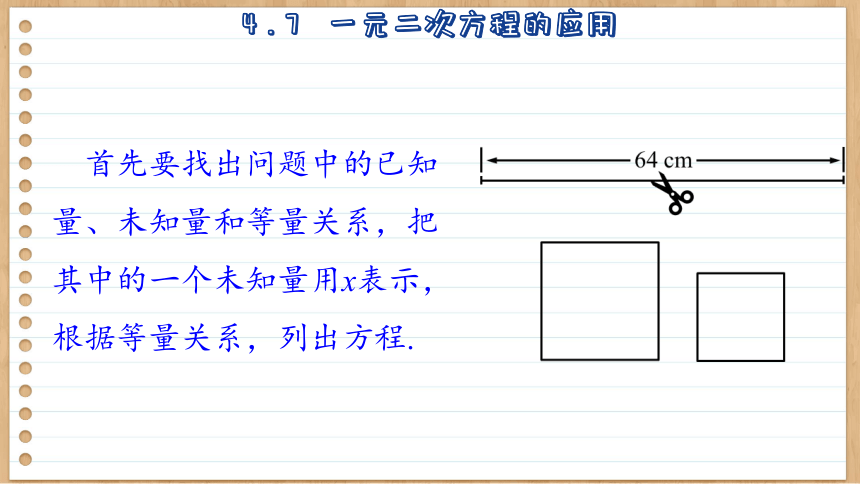
首先要找出问题中的已知量、未知量和等量关系,把其中的一个未知量用x表示,根据等量关系,列出方程.
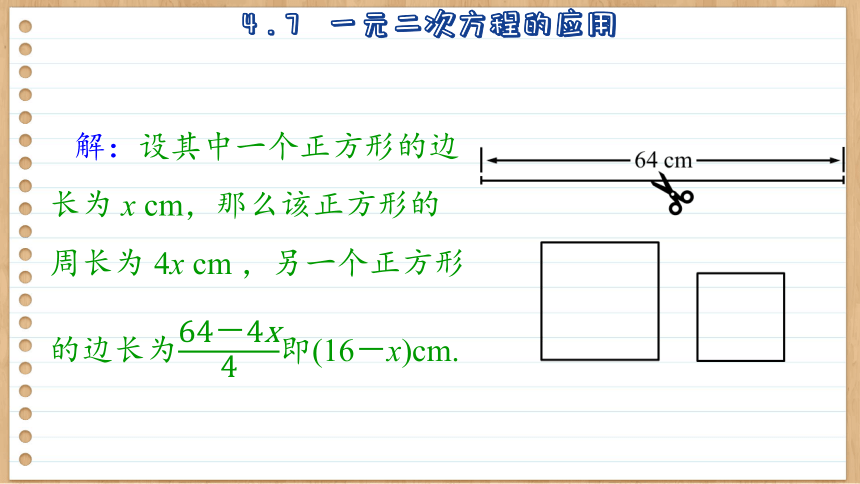
解:设其中一个正方形的边长为 x cm,那么该正方形的周长为 4x cm ,另一个正方形的边长为即(16-x)cm.
根据题意,得
x2+(16-x)2 = 160.
整理,得
x2 - 16x + 48 = 0.
解这个方程,得
x1 = 12,x2 = 4.
当 x1 = 12时,16 - x = 4;
当 x2 = 4 时,16 - x = 12;
经检验,当两个正方形的边长分别是 12 cm 和4cm 时,两个正方形的周长之和为64 cm,面积之和为160 cm. 这就是说,x=12 cm 或 x=4cm 均符合题意.
所以,两个正方形的边长分别为4 cm和12 cm.
列一元二次方程解应用题时,必须检验方程的
根是否符合题意,以决定取舍.
例 2
某花圃用花盆培育某种花卉,经市场调查发现,出售一盆花的盈利与该盆中花的棵数有关. 当每盆栽种3棵时,平均每棵盈利3元. 以同样的栽培条件,每盆增加1棵,平均每棵盈利将减少0.5元. 要使每盆的盈利达到 10元,每盆应当种植该种花卉多少棵
解:设每盆增加种植x棵,则每盆种花 (3+x)棵,平均每棵盈利为(3-0.5x) 元.
根据题意,得(3-0.5x)(3+x) =10.
整理,得 x2-3x+2=0.
解这个方程,得 x1=1,x2=2.
经检验,x1=1或x2=2 均符合题意所以,每盆应种植该种花卉4棵或 5棵.
圆中正方形
我国古代数学家经常用诗歌的形式编写数学题,称为诗题. 清代数学家梅 (jue)成(1681-1763 ) 对明代数学家程大位的《算法统宗》进行修改补充,编著了《增删算法统宗》一书. 在该书第11卷的众多诗题中,有一首“圆中正方形”:
智趣园
今有圆田一块,中间有个方池.
量田特待耕犁,恰好三分在记.
池面至周有数,每边三步无疑.
内方圆径若有知,堪作算中第一.
大意是:有一块圆形的田地,中间有一个正方形水池.量得水池外圆内田地的面积,恰好是 3 分. 从水池的每条边到圆周,最远都是 3 步 (图4-3 ).如果你能求出正方形的边长和圆的直径,那么你的运算能力就数第一了.
本题可以通过列一元二次方程解决. 设正方形的边长为x步,则圆的半径为(+3)步. 在古代,一般取 π≈3.于是,水池外圆内田地的面积为
3(+3)2-x2 = 3×24.
整理,得
x2-36x+180 = 0
练 习
1. 天泉村计划建造如图所示的矩形蔬菜温室. 要求长宽的比为 3∶1. 在温室内,沿前后两侧内墙各留 3 m 宽的空地放置工具,其他两侧内墙各留 1 m 宽的通道当矩形温室的长与宽多少时,蔬菜种植区的面积是 300 m2
解:设矩形温室的宽是 x m,则长是 3x m.
根据题意,得(3x-6)(x-2) =300.
整理,得 x2-4x-96=0.
解得 x1=12,x2=-8.
由题意,知 x2=-8 不符合题意,舍去.
所以 x=12,3x=3×12=36.
所以矩形温室的长是36 m,宽是12m时,蔬菜种植区的面积是 300m2.
2. 如图,矩形ABCD的边AB =200 cm,O为AB的中点.
OE⊥AB交CD于点E. 质点P从点A出发,以2 cm/s的速度沿AB向点B运动; 另一质点Q同时从点O出发,以 3cm/s的速度沿 OE 向点E运动. 经过多少秒时,△POQ 的面积为 1800 cm2
解:设经过 t s 时,△POQ的面积为 1800 cm2.
根据题意,得 (100-2t) ×3t=1 800
或 (2t - 100) × 3t = 1800.
整理,得 t2-50t+600=0或 t2-50t - 600 = 0.
解得 t1= 20,t2 = 30,t3= 60,t4=-10.
经检验 t=-10 不符合题意,舍去.
t=20 或 t=30 或 t=60 均符合题意.
所以经过 20 s,30 s或60 s 时,△POQ 的面积为1 800 cm2.
例 3
某养殖场2010年的产值为 500 万元,2012年的产值为605 万元求2010~2012年该养殖场产值的年平均增长率.
解:设该场2010~2012年产值的年平均增长率为x,那么2011 年的产值为500+500x =500(1+x),2012年的产值为
500 (1+x) +500 (1+x) x=500 (1+x)2
根据题意,得 500 (1+x)2=605.
解这个方程,得 x1=0.1,x2=-2.1.
根据题意,605万元 > 500万元,故年增长率 x>0,而x2=-2.1<0,因此x2=-2.1不符合题意,应当舍去,x1=0.1 符合题意.
所以,该养殖场2010~2012年产值的年平均增长率为0.1,即10%.
例 4
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
解:设该药品平均每次的降价率为x,那么第1次降价后该药品每盒的售价为原售价的(1-x),第2次降价后该药品每盒的售价为原售价的 (1-x)2.
根据问题中的等量关系,得
(1-x)2=64%.
解这个方程,得
x1=0.2,x2=1.8.
根据题意,降价率应满足 0<x<1,因而 x2=1.8 不符合题意,应当舍去而 x1=0.2 符合题意.
所以,该药品平均每次的降价率为0.2,即20%.
挑战自我
例3与例4都是增长率(包括负增长)问题,你能把这类问题中的基本数量关系用公式表示出来吗
例3与例4 这类问题中的基本数量关系可用一元二次方程表示为 a(1±x)2 = b,其中 a 表示起始量, 表示平均增长(或降低)率, 表示增长(或降低)后的终止量,增长用“+”,降低用“一”.
练 习
1. 某农机厂1月份生产联合收割机300 台,为了满足夏收季节市场的需求,3月份比1月份多生产132台. 求2月、3 月两个月的平均月增长率.
解:设2月3月两个月的平均月增长率为z根据题意,得:
300(1+x)2 = 300+132
整理,得 25x2 + 50x - 11 = 0.
解得 x1 = 0.2,x2 = - 2.2.
根据题意,知 x > 0,故 x = - 2.2 舍去.
答:2月、3月两个月的平均月增长率为 20%.
2. 某玩具厂今年每个月的产量都比上个月环比增长同样的百分数,已知该厂今年 4月份的玩具产量为5万件,6月份比5月份多生产了 12 000件.求今年产量的月增长率.
解:设今年产量的月增长率为x. 根据题意,得
5(1+x)2-5(1+x)+1.2.
整理,得 25x2+25x-6 = 0.
解得 x1=0.2,x2=-1.2.
经检验 x2=- 1.2不符合题意,舍去.
答:今年产量的月增长率为 20%.
习题 4.7
复习与巩固
1. 两个实数的和是10,积是-75. 求这两个数.
解:设其中一个数为 x,则另一个数为 10-x.
根据题意,得 x(10-x)=- 75.
整理,得 x2-10x-75=0.
解得 x1=15,x2= - 5;
当x = 15 时,10 - 15 = - 5;
当x=-5时,10 -(-5) = 15.
答:这两个数是 15 和- 5.
2. 如图,在宽为 20 m、长为36 m 的矩形草地上修建两条同样宽且互相垂直的道路,剩余草地的面积是 540 m2. 求道路的宽 (精确到0.1m ).
解:设道路的宽为 x m.
根据题意,得
(20-x)(36-x)=540.
整理,得 x2-56x+180=0.
解得 x =
==28±2.
所以 x1≈3.4,x2≈52.6.
当 x≈52.6时,不符合题意,舍去.
答:道路的宽约为 3.4 m.
3. 如图,AB与BC分别是东西方向和南北方向的道路,AB =1000 m.晨练时,小莹从点A出发,以每分钟150 m的速度向东跑; 小亮同时从点B出发,以每分钟200 m的速度向北跑,经过几分钟时,
他们之间的直线距离仍然是
1000 m
解:设经过 x min时,他们之间的直线距离仍然是1000m.
根据题意得
(1 000 - 150x)2 +(200x)2 = 1 0002.
整理,得 5x2-24x = 0.
解得 x1=0,x2=.
经检验 x1=0 不符合题意,舍去.
答:经过台min时,他们之间的直线距离仍然是1000m.
4. 一本书的长为26 cm,宽为 18.5 cm,厚为1cm.小莹准备用一张面积为1260 cm2的矩形纸包这本书的书皮(如图). 若书皮四周折进的宽度一样,折叠进去的宽度应为多少
解:设折叠进去的宽度为 x cm,
根据题意,得
(18.5×2+1+2x)(26+2x) = 1 260.
整理,得 x2 + 32x - 68 = 0.
解得 x1=-34,x2=2.
经检验 x=- 34 不符合题意,舍去.
答:折叠进去的宽度应为 2 cm.
5. 某种品牌汽车的售价为每辆 10 万元,使用两年后其价
值为 7.225 万元. 求该汽车这两年的年平均折旧率.
解:设该汽车这两年的年平均折旧率为x.
根据题意,得10(1 - x)2 = 7.225,
解得 x1= 1.85,x2 = 0.15.
由题意,知 x1 = 1.85 不符合题意,舍去.
答:该汽车这两年的年平均折旧率为 15%.
6. 解决本章“情境导航”中的问题(精确到0.1%).
解:(1) 设年平均增长率是 x .
根据题意,得 216.5(1 + x)2 - 267.4.
解得 x1≈0.111,x2≈-2.111.
经检验 x2≈-2.111 不符合题意,舍去.
答:从2000 年到 2002 年的两年间,我国荒漠化、沙化土地面积的年平均增长率是 11.1%.
(2) 设年平均降低率为 y.
根据题意,得 267.4(1 - y)2 = 263.6.
解得 y1≈0.007,y2≈1.993.
经检验 y2≈1.993 不符合题意,舍去.
答:从 2002 年到 2004 年的两年间,我国荒漠化、沙化土地的面积亚均每年降低 0.7%.
7. 山青农场去年种了10亩地的南瓜,平均亩产量为
2 000 kg. 根据市场需要,今年该农场扩大了种植面积,并且全部种了高产的新品种南瓜. 已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为 60 000 kg. 求南瓜亩产量的增长率.
解:设南瓜亩产量的增长率为,则种植面积的增长率为 2x,根据题意,得
10(1+ 2x)[2 000(1 + x)] = 60 000.
整理,得 2x2+3x-2 = 0.
解得 x1=0.5,x2= -2.
经检验 x2= -2 不符合题意,舍去.
答:南瓜亩产量的增长率是 50%.
拓展与延伸
8. 一个两位数,十位数字与个位数字的和为5,把十位数字与个位数字互换后得到的两位数与原数的积为 736. 求原两位数.
解:设原两位数的十位数字为 x,则个位数字为 5-x .
根据题意,得
[10x +(5 - x)][10(5 - x) + x] = 736.
整理,得 x2 - 5x + 6 = 0.
解得 x1=2,x2=3.
当x=2时,原两位数是 23;当x=3时,原两位数是 32.
答:原两位数是23或32.
9. 某化肥厂4月份生产某种化肥 500吨,5月份因部分设备检修,产量比4 月份减少了10%. 从6月份起产量逐月上升,7月份达到648吨. 该厂6,7两个月产量的平均月增长率是多少
解:设该厂6,7 两个月产量的平均月增长率是 x .
根据题意,得500(1-10%)(1+x)2=648.
解得 x1=0.2,x2=-2.2.
经检验 x2=-2.2 不符合题意,舍去.
答:该厂6,7 两个月产量的平均月增长率是 20%.
探索与创新
10. 一个容积为1 000 ml的容器里盛满浓度为 80% 的酒精. 第一次倒出若干毫升后,用水加满:第二次又倒出同样毫升数的溶液,再用水加满,这时容器内的酒精的浓度为20%. 求每次倒出溶液多少毫升.
解:设每次倒出溶液 x 毫升.
根据题意,得
1000×80%-1 000×20%=80%x+x.
整理,得 x2-2 000x+750 000=0.
解得 x1=500,x2=1500.
经检验 x=1 500不符合题意,舍去.
答:每次倒出溶液 500 毫升
本课结束
This lesson is over
THANKS!
第4章
一元二次方程
4 . 7
一元二次方程的应用
学习目标
1. 使学生会用列一元二次方程的方法解有关面积、体
积方面的应用问题.
2. 进一步培养学生化实际问题为数学问题的能力和分
析问题解决问题的能力,培养用数学的意识.
交流与发现
与我们学过的一元一次方程、二元一次方程组和分式方程一样,一元二次方程也是刻画现实生活与生产中数量关系的有效模型.
例 1
将一根长为 64 cm的铁丝剪成两段,再将每段分别围成正方形(图4-2),如果两个正方形的面积的和等于160 cm2,求两个正方形的边长.
首先要找出问题中的已知量、未知量和等量关系,把其中的一个未知量用x表示,根据等量关系,列出方程.
解:设其中一个正方形的边长为 x cm,那么该正方形的周长为 4x cm ,另一个正方形的边长为即(16-x)cm.
根据题意,得
x2+(16-x)2 = 160.
整理,得
x2 - 16x + 48 = 0.
解这个方程,得
x1 = 12,x2 = 4.
当 x1 = 12时,16 - x = 4;
当 x2 = 4 时,16 - x = 12;
经检验,当两个正方形的边长分别是 12 cm 和4cm 时,两个正方形的周长之和为64 cm,面积之和为160 cm. 这就是说,x=12 cm 或 x=4cm 均符合题意.
所以,两个正方形的边长分别为4 cm和12 cm.
列一元二次方程解应用题时,必须检验方程的
根是否符合题意,以决定取舍.
例 2
某花圃用花盆培育某种花卉,经市场调查发现,出售一盆花的盈利与该盆中花的棵数有关. 当每盆栽种3棵时,平均每棵盈利3元. 以同样的栽培条件,每盆增加1棵,平均每棵盈利将减少0.5元. 要使每盆的盈利达到 10元,每盆应当种植该种花卉多少棵
解:设每盆增加种植x棵,则每盆种花 (3+x)棵,平均每棵盈利为(3-0.5x) 元.
根据题意,得(3-0.5x)(3+x) =10.
整理,得 x2-3x+2=0.
解这个方程,得 x1=1,x2=2.
经检验,x1=1或x2=2 均符合题意所以,每盆应种植该种花卉4棵或 5棵.
圆中正方形
我国古代数学家经常用诗歌的形式编写数学题,称为诗题. 清代数学家梅 (jue)成(1681-1763 ) 对明代数学家程大位的《算法统宗》进行修改补充,编著了《增删算法统宗》一书. 在该书第11卷的众多诗题中,有一首“圆中正方形”:
智趣园
今有圆田一块,中间有个方池.
量田特待耕犁,恰好三分在记.
池面至周有数,每边三步无疑.
内方圆径若有知,堪作算中第一.
大意是:有一块圆形的田地,中间有一个正方形水池.量得水池外圆内田地的面积,恰好是 3 分. 从水池的每条边到圆周,最远都是 3 步 (图4-3 ).如果你能求出正方形的边长和圆的直径,那么你的运算能力就数第一了.
本题可以通过列一元二次方程解决. 设正方形的边长为x步,则圆的半径为(+3)步. 在古代,一般取 π≈3.于是,水池外圆内田地的面积为
3(+3)2-x2 = 3×24.
整理,得
x2-36x+180 = 0
练 习
1. 天泉村计划建造如图所示的矩形蔬菜温室. 要求长宽的比为 3∶1. 在温室内,沿前后两侧内墙各留 3 m 宽的空地放置工具,其他两侧内墙各留 1 m 宽的通道当矩形温室的长与宽多少时,蔬菜种植区的面积是 300 m2
解:设矩形温室的宽是 x m,则长是 3x m.
根据题意,得(3x-6)(x-2) =300.
整理,得 x2-4x-96=0.
解得 x1=12,x2=-8.
由题意,知 x2=-8 不符合题意,舍去.
所以 x=12,3x=3×12=36.
所以矩形温室的长是36 m,宽是12m时,蔬菜种植区的面积是 300m2.
2. 如图,矩形ABCD的边AB =200 cm,O为AB的中点.
OE⊥AB交CD于点E. 质点P从点A出发,以2 cm/s的速度沿AB向点B运动; 另一质点Q同时从点O出发,以 3cm/s的速度沿 OE 向点E运动. 经过多少秒时,△POQ 的面积为 1800 cm2
解:设经过 t s 时,△POQ的面积为 1800 cm2.
根据题意,得 (100-2t) ×3t=1 800
或 (2t - 100) × 3t = 1800.
整理,得 t2-50t+600=0或 t2-50t - 600 = 0.
解得 t1= 20,t2 = 30,t3= 60,t4=-10.
经检验 t=-10 不符合题意,舍去.
t=20 或 t=30 或 t=60 均符合题意.
所以经过 20 s,30 s或60 s 时,△POQ 的面积为1 800 cm2.
例 3
某养殖场2010年的产值为 500 万元,2012年的产值为605 万元求2010~2012年该养殖场产值的年平均增长率.
解:设该场2010~2012年产值的年平均增长率为x,那么2011 年的产值为500+500x =500(1+x),2012年的产值为
500 (1+x) +500 (1+x) x=500 (1+x)2
根据题意,得 500 (1+x)2=605.
解这个方程,得 x1=0.1,x2=-2.1.
根据题意,605万元 > 500万元,故年增长率 x>0,而x2=-2.1<0,因此x2=-2.1不符合题意,应当舍去,x1=0.1 符合题意.
所以,该养殖场2010~2012年产值的年平均增长率为0.1,即10%.
例 4
某种药品经过两次降价后,每盒售价为原售价的 64%,求该药品平均每次的降价率.
解:设该药品平均每次的降价率为x,那么第1次降价后该药品每盒的售价为原售价的(1-x),第2次降价后该药品每盒的售价为原售价的 (1-x)2.
根据问题中的等量关系,得
(1-x)2=64%.
解这个方程,得
x1=0.2,x2=1.8.
根据题意,降价率应满足 0<x<1,因而 x2=1.8 不符合题意,应当舍去而 x1=0.2 符合题意.
所以,该药品平均每次的降价率为0.2,即20%.
挑战自我
例3与例4都是增长率(包括负增长)问题,你能把这类问题中的基本数量关系用公式表示出来吗
例3与例4 这类问题中的基本数量关系可用一元二次方程表示为 a(1±x)2 = b,其中 a 表示起始量, 表示平均增长(或降低)率, 表示增长(或降低)后的终止量,增长用“+”,降低用“一”.
练 习
1. 某农机厂1月份生产联合收割机300 台,为了满足夏收季节市场的需求,3月份比1月份多生产132台. 求2月、3 月两个月的平均月增长率.
解:设2月3月两个月的平均月增长率为z根据题意,得:
300(1+x)2 = 300+132
整理,得 25x2 + 50x - 11 = 0.
解得 x1 = 0.2,x2 = - 2.2.
根据题意,知 x > 0,故 x = - 2.2 舍去.
答:2月、3月两个月的平均月增长率为 20%.
2. 某玩具厂今年每个月的产量都比上个月环比增长同样的百分数,已知该厂今年 4月份的玩具产量为5万件,6月份比5月份多生产了 12 000件.求今年产量的月增长率.
解:设今年产量的月增长率为x. 根据题意,得
5(1+x)2-5(1+x)+1.2.
整理,得 25x2+25x-6 = 0.
解得 x1=0.2,x2=-1.2.
经检验 x2=- 1.2不符合题意,舍去.
答:今年产量的月增长率为 20%.
习题 4.7
复习与巩固
1. 两个实数的和是10,积是-75. 求这两个数.
解:设其中一个数为 x,则另一个数为 10-x.
根据题意,得 x(10-x)=- 75.
整理,得 x2-10x-75=0.
解得 x1=15,x2= - 5;
当x = 15 时,10 - 15 = - 5;
当x=-5时,10 -(-5) = 15.
答:这两个数是 15 和- 5.
2. 如图,在宽为 20 m、长为36 m 的矩形草地上修建两条同样宽且互相垂直的道路,剩余草地的面积是 540 m2. 求道路的宽 (精确到0.1m ).
解:设道路的宽为 x m.
根据题意,得
(20-x)(36-x)=540.
整理,得 x2-56x+180=0.
解得 x =
==28±2.
所以 x1≈3.4,x2≈52.6.
当 x≈52.6时,不符合题意,舍去.
答:道路的宽约为 3.4 m.
3. 如图,AB与BC分别是东西方向和南北方向的道路,AB =1000 m.晨练时,小莹从点A出发,以每分钟150 m的速度向东跑; 小亮同时从点B出发,以每分钟200 m的速度向北跑,经过几分钟时,
他们之间的直线距离仍然是
1000 m
解:设经过 x min时,他们之间的直线距离仍然是1000m.
根据题意得
(1 000 - 150x)2 +(200x)2 = 1 0002.
整理,得 5x2-24x = 0.
解得 x1=0,x2=.
经检验 x1=0 不符合题意,舍去.
答:经过台min时,他们之间的直线距离仍然是1000m.
4. 一本书的长为26 cm,宽为 18.5 cm,厚为1cm.小莹准备用一张面积为1260 cm2的矩形纸包这本书的书皮(如图). 若书皮四周折进的宽度一样,折叠进去的宽度应为多少
解:设折叠进去的宽度为 x cm,
根据题意,得
(18.5×2+1+2x)(26+2x) = 1 260.
整理,得 x2 + 32x - 68 = 0.
解得 x1=-34,x2=2.
经检验 x=- 34 不符合题意,舍去.
答:折叠进去的宽度应为 2 cm.
5. 某种品牌汽车的售价为每辆 10 万元,使用两年后其价
值为 7.225 万元. 求该汽车这两年的年平均折旧率.
解:设该汽车这两年的年平均折旧率为x.
根据题意,得10(1 - x)2 = 7.225,
解得 x1= 1.85,x2 = 0.15.
由题意,知 x1 = 1.85 不符合题意,舍去.
答:该汽车这两年的年平均折旧率为 15%.
6. 解决本章“情境导航”中的问题(精确到0.1%).
解:(1) 设年平均增长率是 x .
根据题意,得 216.5(1 + x)2 - 267.4.
解得 x1≈0.111,x2≈-2.111.
经检验 x2≈-2.111 不符合题意,舍去.
答:从2000 年到 2002 年的两年间,我国荒漠化、沙化土地面积的年平均增长率是 11.1%.
(2) 设年平均降低率为 y.
根据题意,得 267.4(1 - y)2 = 263.6.
解得 y1≈0.007,y2≈1.993.
经检验 y2≈1.993 不符合题意,舍去.
答:从 2002 年到 2004 年的两年间,我国荒漠化、沙化土地的面积亚均每年降低 0.7%.
7. 山青农场去年种了10亩地的南瓜,平均亩产量为
2 000 kg. 根据市场需要,今年该农场扩大了种植面积,并且全部种了高产的新品种南瓜. 已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为 60 000 kg. 求南瓜亩产量的增长率.
解:设南瓜亩产量的增长率为,则种植面积的增长率为 2x,根据题意,得
10(1+ 2x)[2 000(1 + x)] = 60 000.
整理,得 2x2+3x-2 = 0.
解得 x1=0.5,x2= -2.
经检验 x2= -2 不符合题意,舍去.
答:南瓜亩产量的增长率是 50%.
拓展与延伸
8. 一个两位数,十位数字与个位数字的和为5,把十位数字与个位数字互换后得到的两位数与原数的积为 736. 求原两位数.
解:设原两位数的十位数字为 x,则个位数字为 5-x .
根据题意,得
[10x +(5 - x)][10(5 - x) + x] = 736.
整理,得 x2 - 5x + 6 = 0.
解得 x1=2,x2=3.
当x=2时,原两位数是 23;当x=3时,原两位数是 32.
答:原两位数是23或32.
9. 某化肥厂4月份生产某种化肥 500吨,5月份因部分设备检修,产量比4 月份减少了10%. 从6月份起产量逐月上升,7月份达到648吨. 该厂6,7两个月产量的平均月增长率是多少
解:设该厂6,7 两个月产量的平均月增长率是 x .
根据题意,得500(1-10%)(1+x)2=648.
解得 x1=0.2,x2=-2.2.
经检验 x2=-2.2 不符合题意,舍去.
答:该厂6,7 两个月产量的平均月增长率是 20%.
探索与创新
10. 一个容积为1 000 ml的容器里盛满浓度为 80% 的酒精. 第一次倒出若干毫升后,用水加满:第二次又倒出同样毫升数的溶液,再用水加满,这时容器内的酒精的浓度为20%. 求每次倒出溶液多少毫升.
解:设每次倒出溶液 x 毫升.
根据题意,得
1000×80%-1 000×20%=80%x+x.
整理,得 x2-2 000x+750 000=0.
解得 x1=500,x2=1500.
经检验 x=1 500不符合题意,舍去.
答:每次倒出溶液 500 毫升
本课结束
This lesson is over
THANKS!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
