人教版小学数学六年级下册总复习《统计与概率》质量调研卷(二)(含答案+详细解析)
文档属性
| 名称 | 人教版小学数学六年级下册总复习《统计与概率》质量调研卷(二)(含答案+详细解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 20:57:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版小学数学六年级下册
总复习《统计与概率》质量调研卷(二)
一、选择题(16分)
1.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
2.盒子里有3张10元和2张50元,从盒子中任意摸出两张,总钱数不可能是( )。
A.100元 B.60元 C.40元 D.20元
3.如图是小明家和小芳家2020年家庭支出情况统计图。根据统计图可以对全年教育支出费用进行判断,其中正确的是( )。
A.小明家多 B.小芳家多 C.两家一样多 D.无法判断
4.不透明的袋子里有10个球,分别标注序号1~10。从中任意摸一个,摸到号码是( )的可能性最小。
A.奇数 B.偶数 C.质数 D.合数
5.盒子中放了材质大小相同的99个红球和1个黄球。从中任意摸出一个球,下面说法中合理的是( )。
A.摸出的一定是红球 B.摸出红球的可能性大
C.不可能摸出黄球 D.摸出红球和黄球的可能性相等
6.下面适合用折线统计图表示的是( )。
A.某小学各年级的人数 B.社团兴趣小组人数占总人数的情况
C.小组内5位同学的身高情况 D.校医记录的生病学生体温变化情况
7.淘气所在六(1)班同学的平均身高是143cm,笑笑所在六(2)班同学的平均身高是145.6cm,淘气和笑关的身高相比,( )。
A.淘气更高 B.笑笑更高
C.一样高 D.以上都有可能
8.某班共有48名学生,期末评选一名学习标兵,投票情况如下表所示,下面( )能表示出这个结果。
姓名 欢欢 乐乐 笑笑 平平
票数 24 12 4 8
A. B. C. D.
二、填空题(34分)
9.四个数的平均数是45,去掉一个数,剩下的三个数的平均数43,去掉这个数是( )。
10.要统计花圃里各种花数量所占百分比情况,选用( )统计图最合适。
11.江苏省第七次全国人口普查中,南京和南通两座城市的数据如图:
(1)南京市常住人口数,改写成“万”作单位,是( )万人。南通市常住人口数,省略“万”后面的尾数,约是( )万人。
(2)对比两座城市的数据,下面说法合理的有( )(多选)。
①南京的城镇化程度更高
②南京男女比例相差得更多
③南通的老龄化程度更高
④两座城市都是15—59岁的人数最多
12.李阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜面积分布如右图。其中黄瓜的种植面积是80平方米,请根据统计图回答下面问题。
(1)总的种植面积是( )平方米。
(2)( )的种植面积最大。
(3)番茄的种植面积比黄瓜多( )%。
(4)萝卜的种植面积占( )%,是( )平方米。
13.如图,贾师傅开车从A地经过B地到达C地,办完事后返回。去时在B地稍作停留,返回时不停。去时的车速为每小时48千米/时。
(1)A地到C地之间的路程是( )千米。
(2)返回时的车速是( )千米/时。
14.下图是富春小学各年级段学生人数统计图,已知1-2年级的人数为120人。
(1)富春小学的学生总人数有( )人
(2)3-4年级的学生人数是( )人。
(3)3-4年级的学生人数是5-6年级的学生人数的( )%。
15. “1970年4月24日,中国发射了独立自主研制的第一颗航天器东方红一号卫星,迈出了走向太空的第一步。2020年11月24日到12月17日,嫦娥五号完成了23天的月球采样返回之旅,创造了中国航天史上又一个里程碑式的成就。从东方红一号到嫦娥五号,中国空间技术研究院研制并成功发射了300个航天器,俗称为“三百星”,包括第一颗人造卫星、第一艘飞船、第一颗导航卫星、第一颗月球探测器、第一个空间实验室、第一艘货运飞船……其中,发射第一个“百星”用了41年时间,完成第二个“百星”用了6年时间,而达成第三个“百星”只用了3年时间。”
(1)50年发射300星,平均每年发射( )颗星;
(2)第一个“百星”用了41年,平均每年发射( )颗星;第二个“百星”用了6年,平均每年发射( )颗星;第三个“百星”用了3年,平均每年发射( )颗星。(得数保留一位小数)
(3)看到以上数据的变化,说说你的感想:( )。
16.阳光小学对六年级学生喜欢篮球、舞蹈、书法的情况进行了统计并制成下面两幅统计图(每人只选最喜欢的一项,若三项都不喜欢可以不作选择)。根据图中信息解答:
(1)六年级喜欢这三类活动的男生共有( )人;女生共有( )人,女生喜欢舞蹈的有( )人。
(2)如果阳光小学六年级共有198名学生,那么有( )%的学生这三项活动都不喜欢。(得数保留一位小数)
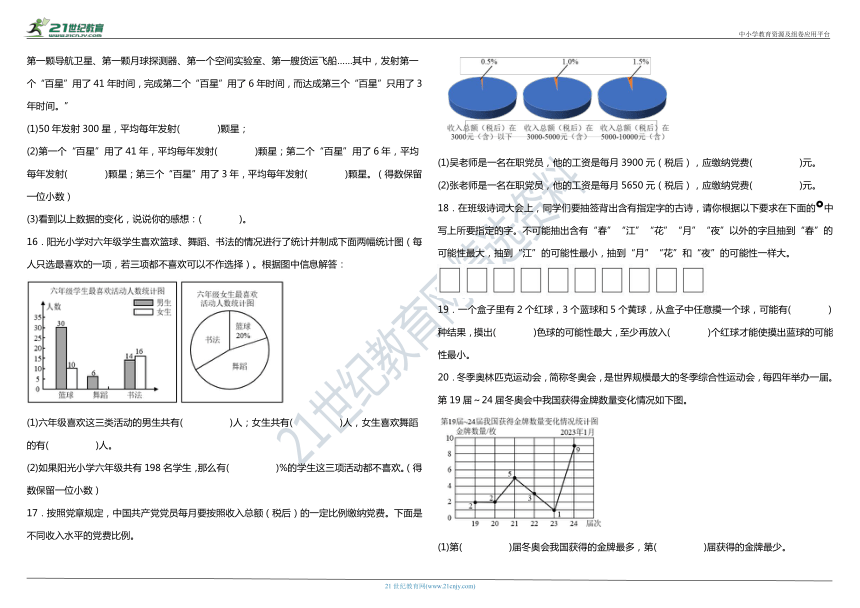
17.按照党章规定,中国共产党党员每月要按照收入总额(税后)的一定比例缴纳党费。下面是不同收入水平的党费比例。
(1)吴老师是一名在职党员,他的工资是每月3900元(税后),应缴纳党费( )元。
(2)张老师是一名在职党员,他的工资是每月5650元(税后),应缴纳党费( )元。
18.在班级诗词大会上,同学们要抽签背出含有指定字的古诗,请你根据以下要求在下面的中写上所要指定的字。不可能抽出含有“春”“江”“花”“月”“夜”以外的字且抽到“春”的可能性最大,抽到“江”的可能性最小,抽到“月”“花”和“夜”的可能性一样大。
19.一个盒子里有2个红球,3个蓝球和5个黄球,从盒子中任意摸一个球,可能有( )种结果,摸出( )色球的可能性最大,至少再放入( )个红球才能使摸出蓝球的可能性最小。
20.冬季奥林匹克运动会,简称冬奥会,是世界规模最大的冬季综合性运动会,每四年举办一届。第19届~24届冬奥会中我国获得金牌数量变化情况如下图。
(1)第( )届冬奥会我国获得的金牌最多,第( )届获得的金牌最少。
(2)第( )届到第( )届冬奥会,我国获得金牌数呈下降趋势。
三、判断题(5分)
21.弟弟比哥哥高。( )
22.一个盒子中装有15只同样的白手套和14只同样的黑手套,从盒子中取出2只手套,一定会是一双白手套或者一双黑手套。( )
23.陈东身高1.62m,在平均水深1.2m的池塘里玩水非常安全。( )
24.学校气象小组要公布上周每天平均气温的高低和变化情况,那么应选用折线统计图比较合适。( )
25.一个不透明的袋子里有2个红球和2个蓝球,每次摸出1个球后再放回,第一次摸出红球,所以第二次摸出蓝球的可能性大。( )
四、作图题(12分)
26.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
27.为开展经典诵读活动,学校购买了一批图书。下面是购买的图书情况统计图,根据信息请将条形统计图和扇形统计图补充完整。
(温馨提示:画出直条后记得标上数据哦!)
28.按要求涂一涂。
(1)摸出的可能是。
(2)摸出的不可能是。
(3)摸出的一定是。
29.“五一”期间,“振大超市”推出有奖促销活动,消费满30元可以参加“转盘”抽奖活动。要求转盘上有“奖20元”“奖5元”“欢迎光临”三个类别,请设计项方案使“奖20元”可能性小于“奖5元”的,“奖5元”的小于“欢迎光临”的。
五、解答题(33分)
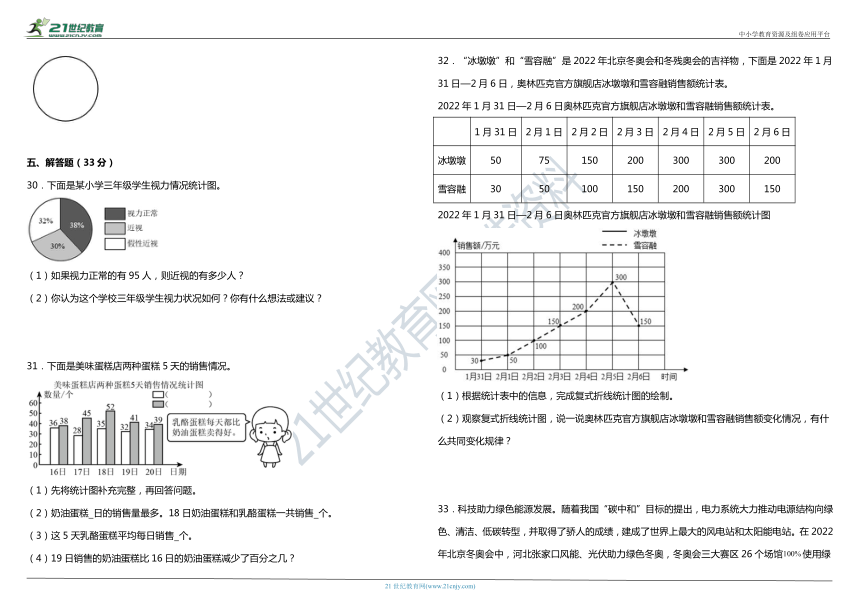
30.下面是某小学三年级学生视力情况统计图。
(1)如果视力正常的有95人,则近视的有多少人?
(2)你认为这个学校三年级学生视力状况如何?你有什么想法或建议?
31.下面是美味蛋糕店两种蛋糕5天的销售情况。
(1)先将统计图补充完整,再回答问题。
(2)奶油蛋糕 日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售 个。
(3)这5天乳酪蛋糕平均每日销售 个。
(4)19日销售的奶油蛋糕比16日的奶油蛋糕减少了百分之几?
32.“冰墩墩”和“雪容融”是2022年北京冬奥会和冬残奥会的吉祥物,下面是2022年1月31日—2月6日,奥林匹克官方旗舰店冰墩墩和雪容融销售额统计表。
2022年1月31日—2月6日奥林匹克官方旗舰店冰墩墩和雪容融销售额统计表。
1月31日 2月1日 2月2日 2月3日 2月4日 2月5日 2月6日
冰墩墩 50 75 150 200 300 300 200
雪容融 30 50 100 150 200 300 150
2022年1月31日—2月6日奥林匹克官方旗舰店冰墩墩和雪容融销售额统计图
(1)根据统计表中的信息,完成复式折线统计图的绘制。
(2)观察复式折线统计图,说一说奥林匹克官方旗舰店冰墩墩和雪容融销售额变化情况,有什么共同变化规律?
33.科技助力绿色能源发展。随着我国“碳中和”目标的提出,电力系统大力推动电源结构向绿色、清洁、低碳转型,并取得了骄人的成绩,建成了世界上最大的风电站和太阳能电站。在2022年北京冬奥会中,河北张家口风能、光伏助力绿色冬奥,冬奥会三大赛区26个场馆使用绿电。未来,接近的传统能源将由水能、风能、太阳能等清洁能源替代。下面是2022年第一季度全国新增发电装机容量统计图。
(1)2022年第一季度全国新增发电装机容量一共( )万千瓦。
(2)请把条形统计图补充完整。
(3)观察统计图,关于几种发电方式,你有什么想说的?
(4)请根据统计图中的信息提出一个用分数解答的问题并解答。(注意:提出一个一步计算的问题,并能正确解答;提出一个二步或二步以上计算的问题,并能正确解答。)
34.垃圾分类是“利国利民”的民生工程,需要全社会的共同参与。下面是某小区2021年下半年生活垃圾未分类垃圾和分类垃圾的质量情况。
(1)根据上面表中的数据绘制复式折线统计图。
(2)七月的未分类垃圾质量占七月垃圾总质量的( )。(填最简分数)
(3)十二月的分类垃圾质量比七月的分类垃圾质量多( )%。
35.表中分别是小莉和小明两位同学5次踢毽的情况统计表和统计图。
小莉5次踢毽的情况统计表
次数 第一次 第二次 第三次 第四次 第五次
个数 10 13 25 27 30
(1)请根据统计表的数据,在统计图中画出小莉踢毽情况的折线统计图。
(2)根据统计图,我们发现共有( )次两人踢毽的个数同样多。
(3)分别计算两人平均每次各踢多少个?
36.下图是某种儿童奶粉的营养成分统计图。如果这种儿童奶粉中含有蛋白质315克,那么含有维生素和矿物质多少克?
37.文峰商场5月份营业额情况如图,已知服饰类的营业额为1440万元。
(1)按规定,商场要按营业额4.5%的税率纳税,文蜂商场5月份共要纳税多少万元?
(2)家电类的营业额比百货类多多少万元?
参考答案:
1.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
2.C
【分析】口袋里有3张10元和2张50元,任意摸出两张,可能摸出两张10元,也可能摸出1张10元和1张50元,还有可能摸出两张50元,据此解答。
【详解】当摸出两张10元时,总钱数是10+10=20(元)
当摸出1张10元和1张50元时,总钱数是10+50=60(元)
当摸出两张50元时,总钱数是50+50=100(元)
则总钱数不可能是40元。
故答案为:C
【点睛】分析题意找出事件发生的所有可能性是解答题目的关键。
3.D
【分析】把小明家、小芳家2020年的家庭支出额分别看作单位“1”,虽然小明家的教育支出占23%,小芳家的教育支出占23%,但是两家的总支出不一定相同,所以无法判断。据此解答。
【详解】虽然小明家、小芳家的教育支出都占23%,但是两家的总支出不一定相同,所以无法判断。
故答案为:D。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.C
【分析】在1~10,10个数字中,奇数有:1、3、5、7、9共5个;偶数有:2、4、6、8、10共5个;质数有:2、3、5、7共4个;合数有:4、6、8、9、10共5个。再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。
【详解】根据分析可知,由于质数只有4个,少于奇数、偶数和合数,所以摸到号码是质数的可能性最小。
不透明的袋子里有10个球,分别标注序号1~10。从中任意摸一个,摸到号码是质数的可能性最小。
故答案为:C
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
5.B
【分析】由于盒子里有两种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,据此解答。
【详解】A.由于盒子里有两种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,所以一定摸出红球是错误的。
B.由于红球的个数最多,所以出红球的可能性最大,是正确的。
C.由于盒子里面有黄球,虽然摸出黄球的可能性小,但不代表不可能摸出黄球,所以这个说法也是错误的。
D.由于盒子里红球多,黄球少,所以出红球的可能性最大,黄球可能性小,所以题干说法是错误的。
因此,说法正确的是摸出红球的可能性最大。
故答案为:B
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
6.D
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】A.某小学各年级的人数可以用条形统计图表示;
B.社团兴趣小组人数占总人数的情况可以用扇形统计图表示;
C.小组内5位同学的身高情况可以用条形统计图表示;
D.校医记录的生病学生体温变化情况可以用折线统计图表示。
故答案为:D
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
7.D
【分析】平均数是反映一组数据的集中趋势的量,不能反映具体数据,据此解答即可。
【详解】淘气所在六(1)班同学的平均身高是143cm,笑笑所在六(2)班同学的平均身高是145.6cm,但是淘气和笑笑之间的高矮关系无法确定。所以淘气和笑关的身高无法进行比较。
故答案为:D
【点睛】本题考查平均数的认识。理解平均数的意义是解决本题的关键。
8.A
【分析】先根据除法的意义,分别计算出四人的票数占总票数的分率,再将四人的票数占总票数的分率与各个选项中的扇形统计图进行比较,即可解答。
【详解】总票数:24+12+4+8
=36+4+8
=40+8
=48(张)
欢欢:24÷48=
乐乐:12÷48=
笑笑:4÷48=
平平:8÷48=
由此可知,欢欢占票数的;乐乐占票数的;笑笑占票数的;平平占票数的,从4个图可以分析出,A图分成4份,其中一份占;一份占;还有两份分别占和,其它的不符合情况。
故答案为:A
【点睛】熟练掌握求一个数占另一个数的几分之几,以及扇形统计图的应用。
9.51
【分析】先根据“平均数×数的个数=总数”分别求出四个数的总数和三个数的总数,进而根据“四个数的总数-三个数的总数=去掉的数”解答即可。
【详解】45×4-43×3
=180-129
=51
所以,去掉的数是51。
【点睛】解答此题应明确:四个数的总数-三个数的总数=去掉的数。
10.扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析可得:要统计花圃里各种花数量所占百分比情况,选用扇形统计图最合适。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
11.(1) 931.4685 773
(2)①②③④
【分析】(1)改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字;
(2)观察图形图结合数据即可求解。
【详解】(1)9314685=931.4685万
7726635≈773万
南京市常住人口数,改写成“万”作单位,是931.4685万人。南通市常住人口数,省略“万”后面的尾数,约是773万人。
(2)①南京的城镇化程度更高的说法合理;
②南京男女比例相差得更多的说法合理;
③南通的老龄化程度更高的说法合理;
④两座城市都是15-59岁的人数最多说法合理。
对比两座城市的数据,下面说法合理的有:①②③④。
【点睛】本题主要考查整数改写和求近似数,注意改写和求近似数时要带计数单位。
12.(1)400
(2)番茄
(3)75
(4) 24 96
【分析】(1)把这块地的面积看作单位“1”,已知黄瓜的面积是80平方米,占这块地的20%,根据已知一个数的百分之几是多少,求这个数,用除法求出这块地的面积;
(2)根据减法的意义,用减法即可求出萝卜的面积占这块地的百分之几,再比较四种蔬菜的种植面积的百分比即可求得哪种蔬菜种植面积大;
(3)以黄瓜所占的20%为单位“1”,用番茄所占的35%减20%,再除以20%,就是番茄的种植面积比黄瓜多的百分率。
(4)根据一个数乘百分数的意义,用乘法求出萝卜面积即可。
【详解】(1)80÷20%=80÷0.2=400(平方米)
总的种植面积是(400)平方米。
(2)萝卜:1-(20%+21%+35%)
=1-76%
=24%
35%>24%>21%>20%
(番茄)的种植面积最大。
(3)(35%-20%)÷20%
=15%÷20%
=75%
番茄的种植面积比黄瓜多(75%)%。
(4)400×24%=96(平方米)
萝卜的种植面积占(24%)%,是(96)平方米。
【点睛】本题主要考查扇形统计图、统计表的特点及应用。
13.(1)432
(2)72
【分析】(1)通过观察折线统计图可知,求时从A地到B地用了3小时,从B地到C地用了6小时,先求出从A地到C地一共用了多少小时,再根据路程=速度×时间,列式解答。
(2)先求出返回用的时间,再根据速度=路程÷时间,列式解答。
【详解】(1)3+(12-6)
=3+6
=9(小时)
48×9=432(千米)
A地到C地之间的路程是432千米。
(2)24﹣18=6(小时)
432÷6=72(千米/时)
返回时的车速是72千米/时。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)480
(2)168
(3)87.5
【分析】(1)由题意可知,1-2年级的人数为120人,占总人数的25%,根据已知一个数的百分之几是多少,求这个数,用除法计算即可;
(2)再根据求一个数的百分之几是多少,用乘法计算,用总人数乘3-4年级的学生人数占总人数的百分率即可求解;
(3)用3-4年级的学生人数占总人数的百分率除以5-6年级的学生人数的百分率即可。
【详解】(1)120÷25%=480(人)
则富春小学的学生总人数有480人。
(2)480×35%=168(人)
则3-4年级的学生人数是168人。
(3)35%÷40%=87.5%
则3-4年级的学生人数是5-6年级的学生人数的87.5%。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题的关键。
15.(1)6
(2) 2.4 16.7 33.3
(3)中国科技在不断进步,我感到非常自豪
【分析】(1)利用平均分的意义,用300÷50即可解答;
(2)利用平均分的意义,用100÷41,求出第一个“百星”用了41年,平均每年发射颗数;用100÷6,求出第二个“百星”用了6年,平均每年发射颗数;用100÷3,求出第三个“百星”用了3年,平均每年发射颗数;
(3)比较三个“百星”年平均发射星的数量,看中国航天科技进步情况。合理即可。
【详解】(1)300÷50=6(颗)
50年发射300星,平均每年发射6颗星。
(2)100÷41≈2.4(颗)
100÷6≈16.7(颗)
100÷3≈33.3(颗)
第一个“百星”用了41年,平均每年发射2.4颗星;第二个“百星”用了6年,平均每年发射16.7颗星;第三个“百星”用了3年,平均每年发射33.3颗星。
(3)看到以上数据的变化,说说你的感想:中国科技在不断进步,我感到非常自豪。
【点睛】本题考查了平均数的计算及求近似数,需正确使用除法法则,计算准确。
16.(1) 50 50 24
(2)49.5
【分析】(1)根据加法的意义,把喜欢篮球、舞蹈、书法的男生人数相加即可求出男生人数;把六年级喜欢篮球、舞蹈、书法的女生人数看作单位“1”,其中喜欢篮球的占20%,是10人,用10÷20%,求出女生人数;再用女生人数减去喜欢篮球的女生人数,减去喜欢书法的女生人数,求出喜欢舞蹈的女生人数;
(2)用阳光小学六年级共有198名学生减去喜欢三项活动的男生人数和女生人数,求出不喜欢三项活动的人数,再用不喜欢三项活动的人数除以总人数,再乘100%,即可解答。
【详解】(1)30+6+14
=36+14
=50(人)
10÷20%=50(人)
50-10-16
=40-16
=24(人)
六年级喜欢这三类活动的男生共有50人;女生有50人,女生喜欢舞蹈的有24人。
(2)(198-50-50)÷198×100%
=(148-50)÷198×100%
=98÷198×100%
≈0.495×100%
=49.5%
如果阳光小学六年级共有198名学生,那么有49.5%的学生这三项活动都不喜欢。
【点睛】本题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)39
(2)84.75
【分析】(1)已知吴老师的工资在3000到5000之间,所以他缴纳的党费占工资的1.0%,把他的工资看作单位“1”,根据百分数乘法的意义,用3900×1.0%即可求出他应缴纳的党费。
(2)已知张老师的工资在5000到10000之间,所以他缴纳的党费占工资的1.5%,把他的工资看作单位“1”,根据百分数乘法的意义,用5650×1.5%即可求出他应缴纳的党费。
【详解】(1)3000<3900<5000
3900×1.0%=39(元)
吴老师应缴纳党费39元。
(2)5000<5650<10000
5650×1.5%=84.75(元)
张老师应缴纳党费84.75元。
【点睛】本题主要考查百分数的应用,明确求一个数的百分之几是多少,用乘法计算。
18.春春春江花花月月夜夜
【分析】一共有10个空格,抽到“江”的可能性最小,则有1个“江”;抽到“月”“花”和“夜”的可能性一样大,则分别有2个“月”“花”和“夜”; 抽到“春”的可能性最大,则有3个“春“。据此可得出答案。
【详解】根据题意可得:有1个“江“字,分别有2个“月”“花”和“夜”,3个”春“字。即:春春春江花花月月夜夜。
【点睛】本题主要考查的是可能性大小的应用,解题的关键是掌握可能性大小与个数的关系,进而得出答案.
19. 3/三 黄 2
【分析】盒子里有几种颜色的球,摸出球的可能性就有几种,盒子里哪种颜色球的数量越多,摸出该种颜色球的可能性就越大,盒子里哪种颜色球的数量越少,摸出该种颜色球的可能性就越小,据此解答。
【详解】盒子里有红球、蓝球、黄球三种颜色的球,从盒子中任意摸一个球,可能有3种结果,因为5>3>2,所以摸出黄色球的可能性最大,2+2=4,3<4<5,至少再放入2个红球才能使摸出蓝球的可能性最小。
【点睛】掌握判断事件发生可能性大小的方法是解答题目的关键。
20.(1) 24 23
(2) 21 23
【分析】(1)观察统计图并比较图中数据可知,第24届冬奥会我国获得的金牌最多,第23届获得的金牌最少。
(2)观察统计图可知,第19届我国获得2枚金牌,第20届我国获得2枚金牌,第21届我国获得5枚金牌,第22届我国获得3枚金牌,第23届我国获得1枚金牌,第24届我国获得9枚金牌,所以,第21届到第23届冬奥会,我国获得金牌数呈下降趋势。
【详解】(1)9>5>3>2>1
第24届冬奥会我国获得的金牌最多,第23届获得的金牌最少。
(2)观察统计图可知,
第21届到第23届冬奥会,我国获得金牌数呈下降趋势。
【点睛】熟练掌握从统计图的数据中获取信息的方法,是解答此题的关键。
21.×
【分析】根据事件的可能性的大小以及事件确定性与不确定性的判断进行解答即可。
【详解】弟弟的年龄比哥哥小,但是身高也有可能比哥哥高,也可能比哥哥矮。原题干说法错误。
故答案为:×
【点睛】解答本题的关键是掌握生活常识。注意生活经验的积累。
22.×
【分析】根据盒子里面手套颜色种类以及数量,从盒子中取出2只手套,会出现的情况有:白手套、白手套;白手套、黑手套;黑手套、黑手套,3种情况中任意一种;据此回答。
【详解】一个盒子中装有15只同样的白手套和14只同样的黑手套,从盒子中取出2只手套,有可能会是一双白手套或者一双黑手套;原题说法错误;
故答案为:×
【点睛】此题考查了可能性的知识,关键理解事件发生会出现的情况都是随机的。
23.×
【分析】平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小。池塘平均水深1.2m,可能有的地方水深超过1.2m很多,甚至能超过1.62m,所以玩水不一定没有危险,据此解答即可。
【详解】由分析可知:
陈东身高1.62m,在平均水深1.2m的池塘里玩水不一定安全。原题干说法错误。
故答案为:×
【点睛】此题主要考查了平均数含义的应用。解答此题的关键是要明确:平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小。
24.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据统计图的特点可知:学校气象小组要公布上周每天平均气温的高低和变化情况,那么应选用折线统计图比较合适。
故答案为:√。
【点睛】能够正确区分各个统计图的特点,根据特点选择合适的统计图。
25.×
【分析】每次摸出1个球后再放回,第二次摸的时候,袋子里也是有2个红球和2个蓝球,摸到红球、蓝球的可能性一样大。
【详解】第二次,摸到红球、蓝球的可能性一样大。
故答案为:×
【点睛】本题的关键是知道怎样判断可能性的大小,与红球、蓝球的数量有关,与上一次的结果没有关系。
26.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
27.见详解
【分析】将总数量看作单位“1”,科技书和连环画的总数量÷对应百分率=总数量;总数量×故事书对应百分率=故事书本数,总数量×其他对应百分率=其他本数,据此补全条形统计图;科技书本数÷总数量=科技书对应百分率,连环画本数÷总数量=连环画对应百分率,据此补全扇形统计图。
【详解】(320+200)÷(1-30%-5%)
=520÷0.65
=800(本)
800×30%=240(本)
800×5%=40(本)
320÷800=40%
200÷800=25%
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
28.(1)见详解;(2)见详解;(3)见详解
【分析】(1)不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。要使一部分是,则选一部分涂色,另一部分不涂色即可;
(2)要使摸出的不可能是,则箱子里没有一个,所以全部涂色即可;
(3)要使摸出的一定是,则箱子里全是,所以全部涂色即可。
【详解】(1)如下图:
(答案不唯一)
(2)如下图:
(3)如下图:
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
29.图见详解
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。所以面积越大,抽到对应奖项的可能性越大,因此要设计“奖20元”抽到的可能性最小,那么它对应的面积要最小,“欢迎光临”抽到的可能性最大,那么它对应的面积要最大,据此填写即可。
【详解】作图如下:
(答案不唯一)
【点睛】本题考查可能性大小的应用,理解不确定事件发生的可能性的大小与事物的数量有关。
30.(1)75人
(2)(答案不唯一)见详解。
【分析】(1)把三年级学生人数看作单位“1”,视力正常的有95人,占三年级学生人数的38%,根据已知一个数的百分之几是多少,求这个数,用除法求出三年级学生人数;再根据一个数乘百分数的意义,用乘法求出近视的人数。
(2)通过观察扇形统计图发现:视力正常的占三年级学生人数的38%,近视的占三年级学生人数的30%,假性近视的占三年级学生人数的32%,这个年级学生视力不正常的人数高达62%,据此数据阐述学生的视力状况,并提出合理的建议(答案不唯一,合理即可)。
【详解】(1)95÷38%×30%
=95÷0.38×0.3
=250×0.3
=75(人);
答:近视的有75人。
(2)我认为这个学校三年级学生的视力状况比较差。这个年级学生视力不正常的人数高达62%,建议学校按时做眼保健操,科学用眼,应让学生养成良好的用眼习惯,防止视力不良率进一步上升(答案不唯一,合理即可)。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
31.(1)见解答
(2)16,87
(3)43
(4)11.1%
【分析】(1)阴影条形每天都比空白条形高,所以阴影条形表示乳酪蛋糕,空白条形表示奶油蛋糕。
(2)奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售多少个用加法计算。
(3)五天的乳酪蛋糕的和除以天数就得平均数。
(4)用16日的奶油蛋糕数量减去19日的奶油蛋糕数量再除以16日的奶油蛋糕数量。
【详解】(1)如图:
(2)35+52=87(个)
奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售87个。
(3)(38+45+52+41+39)÷5
=215÷5
=43(个)
这5天乳酪蛋糕平均每日销售43个。
(4)(36-32)÷36
=4÷36
≈11.1%
答:19日销售的奶油蛋糕比16日的奶油蛋糕减少了11.1%。
【点睛】本题考查了学生对统计图意义的掌握及从统计图中获取信息的意识。
32.(1)见详解;
(2)由复式折线统计图可知,冰墩墩和雪容融销售额都是先增加后减少的变化趋势,最高销售额都是300万元
【分析】(1)统计图中横轴表示时间,纵轴表示销售额,单位长度表示50万元,根据表格中的数据在统计图中找出各对应点,依次连接各点,最后标注数据;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,折线呈上升趋势则销售额逐渐增加,折线呈下降趋势则销售额逐渐减少,据此解答。
【详解】(1)
(2)由复式折线统计图可知,冰墩墩和雪容融销售额都是先增加后减少的变化趋势,最高销售额都是300万元。(答案不唯一)
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
33.(1)3000;
(2)(3)(4)见详解;
【分析】(1)把2022年第一季度全国新增发电装机容量看作单位“1”,其中太阳能发电1320千瓦时,占总量的,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)把2022年第一季度全国新增发电装机容量看作单位“1”,根据减法的意义,用减法求出风电是多少千瓦时,据此完成条形统计图。
(3)答案不唯一。我想说应该加大绿色能源发展的空间,加快绿色能源发展的速度。
(4)答案不唯一。提出的问题是:①第一季度风电发电容量占2022年全国新增发电装机容量的几分之几?用风电发电容量除以总容量即可解答;②火电发电容量比水电发电容量多几分之几?用两种发电容量差除以水电发电容量即可解答。
【详解】(1)
(万千瓦时)
2022年第一季度全国新增发电装机容量一共3000万千瓦时。
(2)
(万千瓦时)
作图如下:
(3)我想说应该加大绿色能源发展的空间,加快绿色能源发展的速度;答案不唯一。
(4)①第一季度风电发电容量占2022年全国新增发电装机容量的几分之几?
780÷3000
=
=
答:第一季度风电发电容量占2022年全国新增发电装机容量的。
②火电发电容量比水电发电容量多几分之几?
(570-330)÷330
=240÷330
=
答:火电发电容量比水电发电容量多。
【点睛】此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
34.(1)见详解
(2)
(3)220
【分析】(1)根据统计表中的数据绘制复式折线统计图。
(2)求出七月垃圾总量,再用七月未分类垃圾的数量除以七月垃圾总量即可。
(3)用十二月的分类垃圾质量减去七月的分类垃圾质量的差,除以七月的分类垃圾质量即可。
【详解】(1)如图:
(2)13÷(13+5)
=13÷18
=
七月的未分类垃圾质量占七月垃圾总质量的。
(3)(16-5)÷5×100%
=11÷5×100%
=2.2×100%
=220%
十二月的分类垃圾质量比七月的分类垃圾质量多220%。
【点睛】本题主要考查统计图表的填充,关键根据统计表中的数据完成统计图并回答问题。
35.(1)见详解;
(2)3;
(3)小莉平均每次踢21个;小明平均每次踢21个。
【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据先描出个点的位置,然后顺次连接各点完成统计图。
(2)根据统计图,我们发现共有3次两人踢毽的个数同样多。
(3)首先根据加法的意义,用加法分别求出小明、小莉5次踢的总数,然后根据求平均数的方法,用除法解答。
【详解】(1)作图如下:
(2)根据统计图,我们发现共有3次两人踢毽的个数同样多。
(3)(15+13+20+27+30)÷5
=(28+20+27+30)÷5
=(48+27+30)÷5
=(75+30)÷5
=105÷5
=21(个)
(10+13+25+27+30)÷5
=(23+25+27+30)÷5
=(48+27+30)÷5
=(75+30)÷5
=105÷5
=21(个)
小莉平均每次踢21个,小明平均每次踢21个。
【点睛】此题考查的目的是理解掌握复式折线统计图的绘制方法及应用,并且根据统计图提供的信息,解决有关的实际问题。
36.35克
【分析】把儿童奶粉的总质量看作单位“1”,已知儿童奶粉中含有蛋白质315克,蛋白质占总质量的45%,根据百分数除法的意义,用315÷45%即可求出儿童奶粉的总质量;又已知维生素和矿物质占总质量的5%,根据百分数乘法的意义,用儿童奶粉的总质量乘5%,即可求出维生素和矿物质的质量。
【详解】315÷45%×5%
=700×5%
=35(克)
答:含有维生素和矿物质35克。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.(1)135万元
(2)660万元
【分析】(1)把文蜂商场5月份营业额看作单位“1”,用1减去百货类营业额占的百分比,减去家电类营业额占的百分比,求出服饰类的营业额占的百分比,用1440元除以服装类占的百分比,求出文蜂商场5月份的营业额,再用5月份的营业额×4.5%,即可得解。
(2)用文蜂商场5月份营业额×家电类的营业额比百货类多占的百分比,即可解答。
【详解】(1)1440÷(1-37%-15%)×4.5%
=1440÷(63%-15%)×4.5%
=1440÷48%×4.5%
=3000×4.5%
=135(万元)
答:文蜂商场5月份共要纳税135万元。
(2)1440÷(1-37%-15%)×(37%-15%)
=1440÷(63%-15%)×22%
=1440÷48%×22%
=3000×22%
=660(万元)
答:家电类的营业额比百货类多660万元。
【点睛】本题考查百分数、分数除法的意义及应用。已知一个数的几分之几是多少,求这个数的计算方法以及求一个数的百分之几是多少的计算方法进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版小学数学六年级下册
总复习《统计与概率》质量调研卷(二)
一、选择题(16分)
1.把下面四张扑克牌反扣在桌面上,并把它们的次序打乱,任意摸一张。下面说法错误的是( )。
A.摸到9的可能性最大
B.摸到9的可能性比7大
C.摸到7和10的可能性一样大
D.摸到7、9和10的可能性一样大
2.盒子里有3张10元和2张50元,从盒子中任意摸出两张,总钱数不可能是( )。
A.100元 B.60元 C.40元 D.20元
3.如图是小明家和小芳家2020年家庭支出情况统计图。根据统计图可以对全年教育支出费用进行判断,其中正确的是( )。
A.小明家多 B.小芳家多 C.两家一样多 D.无法判断
4.不透明的袋子里有10个球,分别标注序号1~10。从中任意摸一个,摸到号码是( )的可能性最小。
A.奇数 B.偶数 C.质数 D.合数
5.盒子中放了材质大小相同的99个红球和1个黄球。从中任意摸出一个球,下面说法中合理的是( )。
A.摸出的一定是红球 B.摸出红球的可能性大
C.不可能摸出黄球 D.摸出红球和黄球的可能性相等
6.下面适合用折线统计图表示的是( )。
A.某小学各年级的人数 B.社团兴趣小组人数占总人数的情况
C.小组内5位同学的身高情况 D.校医记录的生病学生体温变化情况
7.淘气所在六(1)班同学的平均身高是143cm,笑笑所在六(2)班同学的平均身高是145.6cm,淘气和笑关的身高相比,( )。
A.淘气更高 B.笑笑更高
C.一样高 D.以上都有可能
8.某班共有48名学生,期末评选一名学习标兵,投票情况如下表所示,下面( )能表示出这个结果。
姓名 欢欢 乐乐 笑笑 平平
票数 24 12 4 8
A. B. C. D.
二、填空题(34分)
9.四个数的平均数是45,去掉一个数,剩下的三个数的平均数43,去掉这个数是( )。
10.要统计花圃里各种花数量所占百分比情况,选用( )统计图最合适。
11.江苏省第七次全国人口普查中,南京和南通两座城市的数据如图:
(1)南京市常住人口数,改写成“万”作单位,是( )万人。南通市常住人口数,省略“万”后面的尾数,约是( )万人。
(2)对比两座城市的数据,下面说法合理的有( )(多选)。
①南京的城镇化程度更高
②南京男女比例相差得更多
③南通的老龄化程度更高
④两座城市都是15—59岁的人数最多
12.李阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜面积分布如右图。其中黄瓜的种植面积是80平方米,请根据统计图回答下面问题。
(1)总的种植面积是( )平方米。
(2)( )的种植面积最大。
(3)番茄的种植面积比黄瓜多( )%。
(4)萝卜的种植面积占( )%,是( )平方米。
13.如图,贾师傅开车从A地经过B地到达C地,办完事后返回。去时在B地稍作停留,返回时不停。去时的车速为每小时48千米/时。
(1)A地到C地之间的路程是( )千米。
(2)返回时的车速是( )千米/时。
14.下图是富春小学各年级段学生人数统计图,已知1-2年级的人数为120人。
(1)富春小学的学生总人数有( )人
(2)3-4年级的学生人数是( )人。
(3)3-4年级的学生人数是5-6年级的学生人数的( )%。
15. “1970年4月24日,中国发射了独立自主研制的第一颗航天器东方红一号卫星,迈出了走向太空的第一步。2020年11月24日到12月17日,嫦娥五号完成了23天的月球采样返回之旅,创造了中国航天史上又一个里程碑式的成就。从东方红一号到嫦娥五号,中国空间技术研究院研制并成功发射了300个航天器,俗称为“三百星”,包括第一颗人造卫星、第一艘飞船、第一颗导航卫星、第一颗月球探测器、第一个空间实验室、第一艘货运飞船……其中,发射第一个“百星”用了41年时间,完成第二个“百星”用了6年时间,而达成第三个“百星”只用了3年时间。”
(1)50年发射300星,平均每年发射( )颗星;
(2)第一个“百星”用了41年,平均每年发射( )颗星;第二个“百星”用了6年,平均每年发射( )颗星;第三个“百星”用了3年,平均每年发射( )颗星。(得数保留一位小数)
(3)看到以上数据的变化,说说你的感想:( )。
16.阳光小学对六年级学生喜欢篮球、舞蹈、书法的情况进行了统计并制成下面两幅统计图(每人只选最喜欢的一项,若三项都不喜欢可以不作选择)。根据图中信息解答:
(1)六年级喜欢这三类活动的男生共有( )人;女生共有( )人,女生喜欢舞蹈的有( )人。
(2)如果阳光小学六年级共有198名学生,那么有( )%的学生这三项活动都不喜欢。(得数保留一位小数)
17.按照党章规定,中国共产党党员每月要按照收入总额(税后)的一定比例缴纳党费。下面是不同收入水平的党费比例。
(1)吴老师是一名在职党员,他的工资是每月3900元(税后),应缴纳党费( )元。
(2)张老师是一名在职党员,他的工资是每月5650元(税后),应缴纳党费( )元。
18.在班级诗词大会上,同学们要抽签背出含有指定字的古诗,请你根据以下要求在下面的中写上所要指定的字。不可能抽出含有“春”“江”“花”“月”“夜”以外的字且抽到“春”的可能性最大,抽到“江”的可能性最小,抽到“月”“花”和“夜”的可能性一样大。
19.一个盒子里有2个红球,3个蓝球和5个黄球,从盒子中任意摸一个球,可能有( )种结果,摸出( )色球的可能性最大,至少再放入( )个红球才能使摸出蓝球的可能性最小。
20.冬季奥林匹克运动会,简称冬奥会,是世界规模最大的冬季综合性运动会,每四年举办一届。第19届~24届冬奥会中我国获得金牌数量变化情况如下图。
(1)第( )届冬奥会我国获得的金牌最多,第( )届获得的金牌最少。
(2)第( )届到第( )届冬奥会,我国获得金牌数呈下降趋势。
三、判断题(5分)
21.弟弟比哥哥高。( )
22.一个盒子中装有15只同样的白手套和14只同样的黑手套,从盒子中取出2只手套,一定会是一双白手套或者一双黑手套。( )
23.陈东身高1.62m,在平均水深1.2m的池塘里玩水非常安全。( )
24.学校气象小组要公布上周每天平均气温的高低和变化情况,那么应选用折线统计图比较合适。( )
25.一个不透明的袋子里有2个红球和2个蓝球,每次摸出1个球后再放回,第一次摸出红球,所以第二次摸出蓝球的可能性大。( )
四、作图题(12分)
26.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
27.为开展经典诵读活动,学校购买了一批图书。下面是购买的图书情况统计图,根据信息请将条形统计图和扇形统计图补充完整。
(温馨提示:画出直条后记得标上数据哦!)
28.按要求涂一涂。
(1)摸出的可能是。
(2)摸出的不可能是。
(3)摸出的一定是。
29.“五一”期间,“振大超市”推出有奖促销活动,消费满30元可以参加“转盘”抽奖活动。要求转盘上有“奖20元”“奖5元”“欢迎光临”三个类别,请设计项方案使“奖20元”可能性小于“奖5元”的,“奖5元”的小于“欢迎光临”的。
五、解答题(33分)
30.下面是某小学三年级学生视力情况统计图。
(1)如果视力正常的有95人,则近视的有多少人?
(2)你认为这个学校三年级学生视力状况如何?你有什么想法或建议?
31.下面是美味蛋糕店两种蛋糕5天的销售情况。
(1)先将统计图补充完整,再回答问题。
(2)奶油蛋糕 日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售 个。
(3)这5天乳酪蛋糕平均每日销售 个。
(4)19日销售的奶油蛋糕比16日的奶油蛋糕减少了百分之几?
32.“冰墩墩”和“雪容融”是2022年北京冬奥会和冬残奥会的吉祥物,下面是2022年1月31日—2月6日,奥林匹克官方旗舰店冰墩墩和雪容融销售额统计表。
2022年1月31日—2月6日奥林匹克官方旗舰店冰墩墩和雪容融销售额统计表。
1月31日 2月1日 2月2日 2月3日 2月4日 2月5日 2月6日
冰墩墩 50 75 150 200 300 300 200
雪容融 30 50 100 150 200 300 150
2022年1月31日—2月6日奥林匹克官方旗舰店冰墩墩和雪容融销售额统计图
(1)根据统计表中的信息,完成复式折线统计图的绘制。
(2)观察复式折线统计图,说一说奥林匹克官方旗舰店冰墩墩和雪容融销售额变化情况,有什么共同变化规律?
33.科技助力绿色能源发展。随着我国“碳中和”目标的提出,电力系统大力推动电源结构向绿色、清洁、低碳转型,并取得了骄人的成绩,建成了世界上最大的风电站和太阳能电站。在2022年北京冬奥会中,河北张家口风能、光伏助力绿色冬奥,冬奥会三大赛区26个场馆使用绿电。未来,接近的传统能源将由水能、风能、太阳能等清洁能源替代。下面是2022年第一季度全国新增发电装机容量统计图。
(1)2022年第一季度全国新增发电装机容量一共( )万千瓦。
(2)请把条形统计图补充完整。
(3)观察统计图,关于几种发电方式,你有什么想说的?
(4)请根据统计图中的信息提出一个用分数解答的问题并解答。(注意:提出一个一步计算的问题,并能正确解答;提出一个二步或二步以上计算的问题,并能正确解答。)
34.垃圾分类是“利国利民”的民生工程,需要全社会的共同参与。下面是某小区2021年下半年生活垃圾未分类垃圾和分类垃圾的质量情况。
(1)根据上面表中的数据绘制复式折线统计图。
(2)七月的未分类垃圾质量占七月垃圾总质量的( )。(填最简分数)
(3)十二月的分类垃圾质量比七月的分类垃圾质量多( )%。
35.表中分别是小莉和小明两位同学5次踢毽的情况统计表和统计图。
小莉5次踢毽的情况统计表
次数 第一次 第二次 第三次 第四次 第五次
个数 10 13 25 27 30
(1)请根据统计表的数据,在统计图中画出小莉踢毽情况的折线统计图。
(2)根据统计图,我们发现共有( )次两人踢毽的个数同样多。
(3)分别计算两人平均每次各踢多少个?
36.下图是某种儿童奶粉的营养成分统计图。如果这种儿童奶粉中含有蛋白质315克,那么含有维生素和矿物质多少克?
37.文峰商场5月份营业额情况如图,已知服饰类的营业额为1440万元。
(1)按规定,商场要按营业额4.5%的税率纳税,文蜂商场5月份共要纳税多少万元?
(2)家电类的营业额比百货类多多少万元?
参考答案:
1.D
【分析】从图中可知,9有2张,7有1张,10有1张;根据可能性大小的判断方法,数量最多的,摸到的可能性最大;反之,数量最少的,摸到的可能性就最小;数量相等的,摸到的可能性一样大。
【详解】A.9的张数最多,所以摸到9的可能性最大,原题说法正确;
B.9的张数比7的张数多,所以摸到9的可能性比7大,原题说法正确;
C.7和10的张数一样多,所以摸到7和10的可能性一样大,原题说法正确;
D.7、9、10的张数不一样多,所以摸到7、9和10的可能性不一样大,原题说法错误。
故答案为:D
【点睛】本题考查可能性的大小,根据事件数量的多少判断可能性的大小。
2.C
【分析】口袋里有3张10元和2张50元,任意摸出两张,可能摸出两张10元,也可能摸出1张10元和1张50元,还有可能摸出两张50元,据此解答。
【详解】当摸出两张10元时,总钱数是10+10=20(元)
当摸出1张10元和1张50元时,总钱数是10+50=60(元)
当摸出两张50元时,总钱数是50+50=100(元)
则总钱数不可能是40元。
故答案为:C
【点睛】分析题意找出事件发生的所有可能性是解答题目的关键。
3.D
【分析】把小明家、小芳家2020年的家庭支出额分别看作单位“1”,虽然小明家的教育支出占23%,小芳家的教育支出占23%,但是两家的总支出不一定相同,所以无法判断。据此解答。
【详解】虽然小明家、小芳家的教育支出都占23%,但是两家的总支出不一定相同,所以无法判断。
故答案为:D。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
4.C
【分析】在1~10,10个数字中,奇数有:1、3、5、7、9共5个;偶数有:2、4、6、8、10共5个;质数有:2、3、5、7共4个;合数有:4、6、8、9、10共5个。再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。
【详解】根据分析可知,由于质数只有4个,少于奇数、偶数和合数,所以摸到号码是质数的可能性最小。
不透明的袋子里有10个球,分别标注序号1~10。从中任意摸一个,摸到号码是质数的可能性最小。
故答案为:C
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
5.B
【分析】由于盒子里有两种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,据此解答。
【详解】A.由于盒子里有两种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,所以一定摸出红球是错误的。
B.由于红球的个数最多,所以出红球的可能性最大,是正确的。
C.由于盒子里面有黄球,虽然摸出黄球的可能性小,但不代表不可能摸出黄球,所以这个说法也是错误的。
D.由于盒子里红球多,黄球少,所以出红球的可能性最大,黄球可能性小,所以题干说法是错误的。
因此,说法正确的是摸出红球的可能性最大。
故答案为:B
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
6.D
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】A.某小学各年级的人数可以用条形统计图表示;
B.社团兴趣小组人数占总人数的情况可以用扇形统计图表示;
C.小组内5位同学的身高情况可以用条形统计图表示;
D.校医记录的生病学生体温变化情况可以用折线统计图表示。
故答案为:D
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
7.D
【分析】平均数是反映一组数据的集中趋势的量,不能反映具体数据,据此解答即可。
【详解】淘气所在六(1)班同学的平均身高是143cm,笑笑所在六(2)班同学的平均身高是145.6cm,但是淘气和笑笑之间的高矮关系无法确定。所以淘气和笑关的身高无法进行比较。
故答案为:D
【点睛】本题考查平均数的认识。理解平均数的意义是解决本题的关键。
8.A
【分析】先根据除法的意义,分别计算出四人的票数占总票数的分率,再将四人的票数占总票数的分率与各个选项中的扇形统计图进行比较,即可解答。
【详解】总票数:24+12+4+8
=36+4+8
=40+8
=48(张)
欢欢:24÷48=
乐乐:12÷48=
笑笑:4÷48=
平平:8÷48=
由此可知,欢欢占票数的;乐乐占票数的;笑笑占票数的;平平占票数的,从4个图可以分析出,A图分成4份,其中一份占;一份占;还有两份分别占和,其它的不符合情况。
故答案为:A
【点睛】熟练掌握求一个数占另一个数的几分之几,以及扇形统计图的应用。
9.51
【分析】先根据“平均数×数的个数=总数”分别求出四个数的总数和三个数的总数,进而根据“四个数的总数-三个数的总数=去掉的数”解答即可。
【详解】45×4-43×3
=180-129
=51
所以,去掉的数是51。
【点睛】解答此题应明确:四个数的总数-三个数的总数=去掉的数。
10.扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析可得:要统计花圃里各种花数量所占百分比情况,选用扇形统计图最合适。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
11.(1) 931.4685 773
(2)①②③④
【分析】(1)改写成用“万”作单位的数,就是在万位数的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上“万”字;省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字;
(2)观察图形图结合数据即可求解。
【详解】(1)9314685=931.4685万
7726635≈773万
南京市常住人口数,改写成“万”作单位,是931.4685万人。南通市常住人口数,省略“万”后面的尾数,约是773万人。
(2)①南京的城镇化程度更高的说法合理;
②南京男女比例相差得更多的说法合理;
③南通的老龄化程度更高的说法合理;
④两座城市都是15-59岁的人数最多说法合理。
对比两座城市的数据,下面说法合理的有:①②③④。
【点睛】本题主要考查整数改写和求近似数,注意改写和求近似数时要带计数单位。
12.(1)400
(2)番茄
(3)75
(4) 24 96
【分析】(1)把这块地的面积看作单位“1”,已知黄瓜的面积是80平方米,占这块地的20%,根据已知一个数的百分之几是多少,求这个数,用除法求出这块地的面积;
(2)根据减法的意义,用减法即可求出萝卜的面积占这块地的百分之几,再比较四种蔬菜的种植面积的百分比即可求得哪种蔬菜种植面积大;
(3)以黄瓜所占的20%为单位“1”,用番茄所占的35%减20%,再除以20%,就是番茄的种植面积比黄瓜多的百分率。
(4)根据一个数乘百分数的意义,用乘法求出萝卜面积即可。
【详解】(1)80÷20%=80÷0.2=400(平方米)
总的种植面积是(400)平方米。
(2)萝卜:1-(20%+21%+35%)
=1-76%
=24%
35%>24%>21%>20%
(番茄)的种植面积最大。
(3)(35%-20%)÷20%
=15%÷20%
=75%
番茄的种植面积比黄瓜多(75%)%。
(4)400×24%=96(平方米)
萝卜的种植面积占(24%)%,是(96)平方米。
【点睛】本题主要考查扇形统计图、统计表的特点及应用。
13.(1)432
(2)72
【分析】(1)通过观察折线统计图可知,求时从A地到B地用了3小时,从B地到C地用了6小时,先求出从A地到C地一共用了多少小时,再根据路程=速度×时间,列式解答。
(2)先求出返回用的时间,再根据速度=路程÷时间,列式解答。
【详解】(1)3+(12-6)
=3+6
=9(小时)
48×9=432(千米)
A地到C地之间的路程是432千米。
(2)24﹣18=6(小时)
432÷6=72(千米/时)
返回时的车速是72千米/时。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
14.(1)480
(2)168
(3)87.5
【分析】(1)由题意可知,1-2年级的人数为120人,占总人数的25%,根据已知一个数的百分之几是多少,求这个数,用除法计算即可;
(2)再根据求一个数的百分之几是多少,用乘法计算,用总人数乘3-4年级的学生人数占总人数的百分率即可求解;
(3)用3-4年级的学生人数占总人数的百分率除以5-6年级的学生人数的百分率即可。
【详解】(1)120÷25%=480(人)
则富春小学的学生总人数有480人。
(2)480×35%=168(人)
则3-4年级的学生人数是168人。
(3)35%÷40%=87.5%
则3-4年级的学生人数是5-6年级的学生人数的87.5%。
【点睛】本题考查已知一个数的百分之几是多少,求这个数,明确用除法是解题的关键。
15.(1)6
(2) 2.4 16.7 33.3
(3)中国科技在不断进步,我感到非常自豪
【分析】(1)利用平均分的意义,用300÷50即可解答;
(2)利用平均分的意义,用100÷41,求出第一个“百星”用了41年,平均每年发射颗数;用100÷6,求出第二个“百星”用了6年,平均每年发射颗数;用100÷3,求出第三个“百星”用了3年,平均每年发射颗数;
(3)比较三个“百星”年平均发射星的数量,看中国航天科技进步情况。合理即可。
【详解】(1)300÷50=6(颗)
50年发射300星,平均每年发射6颗星。
(2)100÷41≈2.4(颗)
100÷6≈16.7(颗)
100÷3≈33.3(颗)
第一个“百星”用了41年,平均每年发射2.4颗星;第二个“百星”用了6年,平均每年发射16.7颗星;第三个“百星”用了3年,平均每年发射33.3颗星。
(3)看到以上数据的变化,说说你的感想:中国科技在不断进步,我感到非常自豪。
【点睛】本题考查了平均数的计算及求近似数,需正确使用除法法则,计算准确。
16.(1) 50 50 24
(2)49.5
【分析】(1)根据加法的意义,把喜欢篮球、舞蹈、书法的男生人数相加即可求出男生人数;把六年级喜欢篮球、舞蹈、书法的女生人数看作单位“1”,其中喜欢篮球的占20%,是10人,用10÷20%,求出女生人数;再用女生人数减去喜欢篮球的女生人数,减去喜欢书法的女生人数,求出喜欢舞蹈的女生人数;
(2)用阳光小学六年级共有198名学生减去喜欢三项活动的男生人数和女生人数,求出不喜欢三项活动的人数,再用不喜欢三项活动的人数除以总人数,再乘100%,即可解答。
【详解】(1)30+6+14
=36+14
=50(人)
10÷20%=50(人)
50-10-16
=40-16
=24(人)
六年级喜欢这三类活动的男生共有50人;女生有50人,女生喜欢舞蹈的有24人。
(2)(198-50-50)÷198×100%
=(148-50)÷198×100%
=98÷198×100%
≈0.495×100%
=49.5%
如果阳光小学六年级共有198名学生,那么有49.5%的学生这三项活动都不喜欢。
【点睛】本题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
17.(1)39
(2)84.75
【分析】(1)已知吴老师的工资在3000到5000之间,所以他缴纳的党费占工资的1.0%,把他的工资看作单位“1”,根据百分数乘法的意义,用3900×1.0%即可求出他应缴纳的党费。
(2)已知张老师的工资在5000到10000之间,所以他缴纳的党费占工资的1.5%,把他的工资看作单位“1”,根据百分数乘法的意义,用5650×1.5%即可求出他应缴纳的党费。
【详解】(1)3000<3900<5000
3900×1.0%=39(元)
吴老师应缴纳党费39元。
(2)5000<5650<10000
5650×1.5%=84.75(元)
张老师应缴纳党费84.75元。
【点睛】本题主要考查百分数的应用,明确求一个数的百分之几是多少,用乘法计算。
18.春春春江花花月月夜夜
【分析】一共有10个空格,抽到“江”的可能性最小,则有1个“江”;抽到“月”“花”和“夜”的可能性一样大,则分别有2个“月”“花”和“夜”; 抽到“春”的可能性最大,则有3个“春“。据此可得出答案。
【详解】根据题意可得:有1个“江“字,分别有2个“月”“花”和“夜”,3个”春“字。即:春春春江花花月月夜夜。
【点睛】本题主要考查的是可能性大小的应用,解题的关键是掌握可能性大小与个数的关系,进而得出答案.
19. 3/三 黄 2
【分析】盒子里有几种颜色的球,摸出球的可能性就有几种,盒子里哪种颜色球的数量越多,摸出该种颜色球的可能性就越大,盒子里哪种颜色球的数量越少,摸出该种颜色球的可能性就越小,据此解答。
【详解】盒子里有红球、蓝球、黄球三种颜色的球,从盒子中任意摸一个球,可能有3种结果,因为5>3>2,所以摸出黄色球的可能性最大,2+2=4,3<4<5,至少再放入2个红球才能使摸出蓝球的可能性最小。
【点睛】掌握判断事件发生可能性大小的方法是解答题目的关键。
20.(1) 24 23
(2) 21 23
【分析】(1)观察统计图并比较图中数据可知,第24届冬奥会我国获得的金牌最多,第23届获得的金牌最少。
(2)观察统计图可知,第19届我国获得2枚金牌,第20届我国获得2枚金牌,第21届我国获得5枚金牌,第22届我国获得3枚金牌,第23届我国获得1枚金牌,第24届我国获得9枚金牌,所以,第21届到第23届冬奥会,我国获得金牌数呈下降趋势。
【详解】(1)9>5>3>2>1
第24届冬奥会我国获得的金牌最多,第23届获得的金牌最少。
(2)观察统计图可知,
第21届到第23届冬奥会,我国获得金牌数呈下降趋势。
【点睛】熟练掌握从统计图的数据中获取信息的方法,是解答此题的关键。
21.×
【分析】根据事件的可能性的大小以及事件确定性与不确定性的判断进行解答即可。
【详解】弟弟的年龄比哥哥小,但是身高也有可能比哥哥高,也可能比哥哥矮。原题干说法错误。
故答案为:×
【点睛】解答本题的关键是掌握生活常识。注意生活经验的积累。
22.×
【分析】根据盒子里面手套颜色种类以及数量,从盒子中取出2只手套,会出现的情况有:白手套、白手套;白手套、黑手套;黑手套、黑手套,3种情况中任意一种;据此回答。
【详解】一个盒子中装有15只同样的白手套和14只同样的黑手套,从盒子中取出2只手套,有可能会是一双白手套或者一双黑手套;原题说法错误;
故答案为:×
【点睛】此题考查了可能性的知识,关键理解事件发生会出现的情况都是随机的。
23.×
【分析】平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小。池塘平均水深1.2m,可能有的地方水深超过1.2m很多,甚至能超过1.62m,所以玩水不一定没有危险,据此解答即可。
【详解】由分析可知:
陈东身高1.62m,在平均水深1.2m的池塘里玩水不一定安全。原题干说法错误。
故答案为:×
【点睛】此题主要考查了平均数含义的应用。解答此题的关键是要明确:平均数只能反映一组数据的平均水平,并不能反映这组数据的中所有数据的大小。
24.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据统计图的特点可知:学校气象小组要公布上周每天平均气温的高低和变化情况,那么应选用折线统计图比较合适。
故答案为:√。
【点睛】能够正确区分各个统计图的特点,根据特点选择合适的统计图。
25.×
【分析】每次摸出1个球后再放回,第二次摸的时候,袋子里也是有2个红球和2个蓝球,摸到红球、蓝球的可能性一样大。
【详解】第二次,摸到红球、蓝球的可能性一样大。
故答案为:×
【点睛】本题的关键是知道怎样判断可能性的大小,与红球、蓝球的数量有关,与上一次的结果没有关系。
26.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
27.见详解
【分析】将总数量看作单位“1”,科技书和连环画的总数量÷对应百分率=总数量;总数量×故事书对应百分率=故事书本数,总数量×其他对应百分率=其他本数,据此补全条形统计图;科技书本数÷总数量=科技书对应百分率,连环画本数÷总数量=连环画对应百分率,据此补全扇形统计图。
【详解】(320+200)÷(1-30%-5%)
=520÷0.65
=800(本)
800×30%=240(本)
800×5%=40(本)
320÷800=40%
200÷800=25%
【点睛】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
28.(1)见详解;(2)见详解;(3)见详解
【分析】(1)不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。要使一部分是,则选一部分涂色,另一部分不涂色即可;
(2)要使摸出的不可能是,则箱子里没有一个,所以全部涂色即可;
(3)要使摸出的一定是,则箱子里全是,所以全部涂色即可。
【详解】(1)如下图:
(答案不唯一)
(2)如下图:
(3)如下图:
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关。
29.图见详解
【分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小。所以面积越大,抽到对应奖项的可能性越大,因此要设计“奖20元”抽到的可能性最小,那么它对应的面积要最小,“欢迎光临”抽到的可能性最大,那么它对应的面积要最大,据此填写即可。
【详解】作图如下:
(答案不唯一)
【点睛】本题考查可能性大小的应用,理解不确定事件发生的可能性的大小与事物的数量有关。
30.(1)75人
(2)(答案不唯一)见详解。
【分析】(1)把三年级学生人数看作单位“1”,视力正常的有95人,占三年级学生人数的38%,根据已知一个数的百分之几是多少,求这个数,用除法求出三年级学生人数;再根据一个数乘百分数的意义,用乘法求出近视的人数。
(2)通过观察扇形统计图发现:视力正常的占三年级学生人数的38%,近视的占三年级学生人数的30%,假性近视的占三年级学生人数的32%,这个年级学生视力不正常的人数高达62%,据此数据阐述学生的视力状况,并提出合理的建议(答案不唯一,合理即可)。
【详解】(1)95÷38%×30%
=95÷0.38×0.3
=250×0.3
=75(人);
答:近视的有75人。
(2)我认为这个学校三年级学生的视力状况比较差。这个年级学生视力不正常的人数高达62%,建议学校按时做眼保健操,科学用眼,应让学生养成良好的用眼习惯,防止视力不良率进一步上升(答案不唯一,合理即可)。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
31.(1)见解答
(2)16,87
(3)43
(4)11.1%
【分析】(1)阴影条形每天都比空白条形高,所以阴影条形表示乳酪蛋糕,空白条形表示奶油蛋糕。
(2)奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售多少个用加法计算。
(3)五天的乳酪蛋糕的和除以天数就得平均数。
(4)用16日的奶油蛋糕数量减去19日的奶油蛋糕数量再除以16日的奶油蛋糕数量。
【详解】(1)如图:
(2)35+52=87(个)
奶油蛋糕16日的销售量最多。18日奶油蛋糕和乳酪蛋糕一共销售87个。
(3)(38+45+52+41+39)÷5
=215÷5
=43(个)
这5天乳酪蛋糕平均每日销售43个。
(4)(36-32)÷36
=4÷36
≈11.1%
答:19日销售的奶油蛋糕比16日的奶油蛋糕减少了11.1%。
【点睛】本题考查了学生对统计图意义的掌握及从统计图中获取信息的意识。
32.(1)见详解;
(2)由复式折线统计图可知,冰墩墩和雪容融销售额都是先增加后减少的变化趋势,最高销售额都是300万元
【分析】(1)统计图中横轴表示时间,纵轴表示销售额,单位长度表示50万元,根据表格中的数据在统计图中找出各对应点,依次连接各点,最后标注数据;
(2)复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况,折线呈上升趋势则销售额逐渐增加,折线呈下降趋势则销售额逐渐减少,据此解答。
【详解】(1)
(2)由复式折线统计图可知,冰墩墩和雪容融销售额都是先增加后减少的变化趋势,最高销售额都是300万元。(答案不唯一)
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
33.(1)3000;
(2)(3)(4)见详解;
【分析】(1)把2022年第一季度全国新增发电装机容量看作单位“1”,其中太阳能发电1320千瓦时,占总量的,根据已知一个数的百分之几是多少,求这个数,用除法解答。
(2)把2022年第一季度全国新增发电装机容量看作单位“1”,根据减法的意义,用减法求出风电是多少千瓦时,据此完成条形统计图。
(3)答案不唯一。我想说应该加大绿色能源发展的空间,加快绿色能源发展的速度。
(4)答案不唯一。提出的问题是:①第一季度风电发电容量占2022年全国新增发电装机容量的几分之几?用风电发电容量除以总容量即可解答;②火电发电容量比水电发电容量多几分之几?用两种发电容量差除以水电发电容量即可解答。
【详解】(1)
(万千瓦时)
2022年第一季度全国新增发电装机容量一共3000万千瓦时。
(2)
(万千瓦时)
作图如下:
(3)我想说应该加大绿色能源发展的空间,加快绿色能源发展的速度;答案不唯一。
(4)①第一季度风电发电容量占2022年全国新增发电装机容量的几分之几?
780÷3000
=
=
答:第一季度风电发电容量占2022年全国新增发电装机容量的。
②火电发电容量比水电发电容量多几分之几?
(570-330)÷330
=240÷330
=
答:火电发电容量比水电发电容量多。
【点睛】此题考查的目的是理解掌握扇形统计图、条形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
34.(1)见详解
(2)
(3)220
【分析】(1)根据统计表中的数据绘制复式折线统计图。
(2)求出七月垃圾总量,再用七月未分类垃圾的数量除以七月垃圾总量即可。
(3)用十二月的分类垃圾质量减去七月的分类垃圾质量的差,除以七月的分类垃圾质量即可。
【详解】(1)如图:
(2)13÷(13+5)
=13÷18
=
七月的未分类垃圾质量占七月垃圾总质量的。
(3)(16-5)÷5×100%
=11÷5×100%
=2.2×100%
=220%
十二月的分类垃圾质量比七月的分类垃圾质量多220%。
【点睛】本题主要考查统计图表的填充,关键根据统计表中的数据完成统计图并回答问题。
35.(1)见详解;
(2)3;
(3)小莉平均每次踢21个;小明平均每次踢21个。
【分析】(1)根据折线统计图的绘制方法,按照统计表中的数据先描出个点的位置,然后顺次连接各点完成统计图。
(2)根据统计图,我们发现共有3次两人踢毽的个数同样多。
(3)首先根据加法的意义,用加法分别求出小明、小莉5次踢的总数,然后根据求平均数的方法,用除法解答。
【详解】(1)作图如下:
(2)根据统计图,我们发现共有3次两人踢毽的个数同样多。
(3)(15+13+20+27+30)÷5
=(28+20+27+30)÷5
=(48+27+30)÷5
=(75+30)÷5
=105÷5
=21(个)
(10+13+25+27+30)÷5
=(23+25+27+30)÷5
=(48+27+30)÷5
=(75+30)÷5
=105÷5
=21(个)
小莉平均每次踢21个,小明平均每次踢21个。
【点睛】此题考查的目的是理解掌握复式折线统计图的绘制方法及应用,并且根据统计图提供的信息,解决有关的实际问题。
36.35克
【分析】把儿童奶粉的总质量看作单位“1”,已知儿童奶粉中含有蛋白质315克,蛋白质占总质量的45%,根据百分数除法的意义,用315÷45%即可求出儿童奶粉的总质量;又已知维生素和矿物质占总质量的5%,根据百分数乘法的意义,用儿童奶粉的总质量乘5%,即可求出维生素和矿物质的质量。
【详解】315÷45%×5%
=700×5%
=35(克)
答:含有维生素和矿物质35克。
【点睛】此题考査的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.(1)135万元
(2)660万元
【分析】(1)把文蜂商场5月份营业额看作单位“1”,用1减去百货类营业额占的百分比,减去家电类营业额占的百分比,求出服饰类的营业额占的百分比,用1440元除以服装类占的百分比,求出文蜂商场5月份的营业额,再用5月份的营业额×4.5%,即可得解。
(2)用文蜂商场5月份营业额×家电类的营业额比百货类多占的百分比,即可解答。
【详解】(1)1440÷(1-37%-15%)×4.5%
=1440÷(63%-15%)×4.5%
=1440÷48%×4.5%
=3000×4.5%
=135(万元)
答:文蜂商场5月份共要纳税135万元。
(2)1440÷(1-37%-15%)×(37%-15%)
=1440÷(63%-15%)×22%
=1440÷48%×22%
=3000×22%
=660(万元)
答:家电类的营业额比百货类多660万元。
【点睛】本题考查百分数、分数除法的意义及应用。已知一个数的几分之几是多少,求这个数的计算方法以及求一个数的百分之几是多少的计算方法进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
