人教版小学数学六年级下册总复习《图形与几何》单元专项训练——应用题(含答案+详细解析)
文档属性
| 名称 | 人教版小学数学六年级下册总复习《图形与几何》单元专项训练——应用题(含答案+详细解析) | 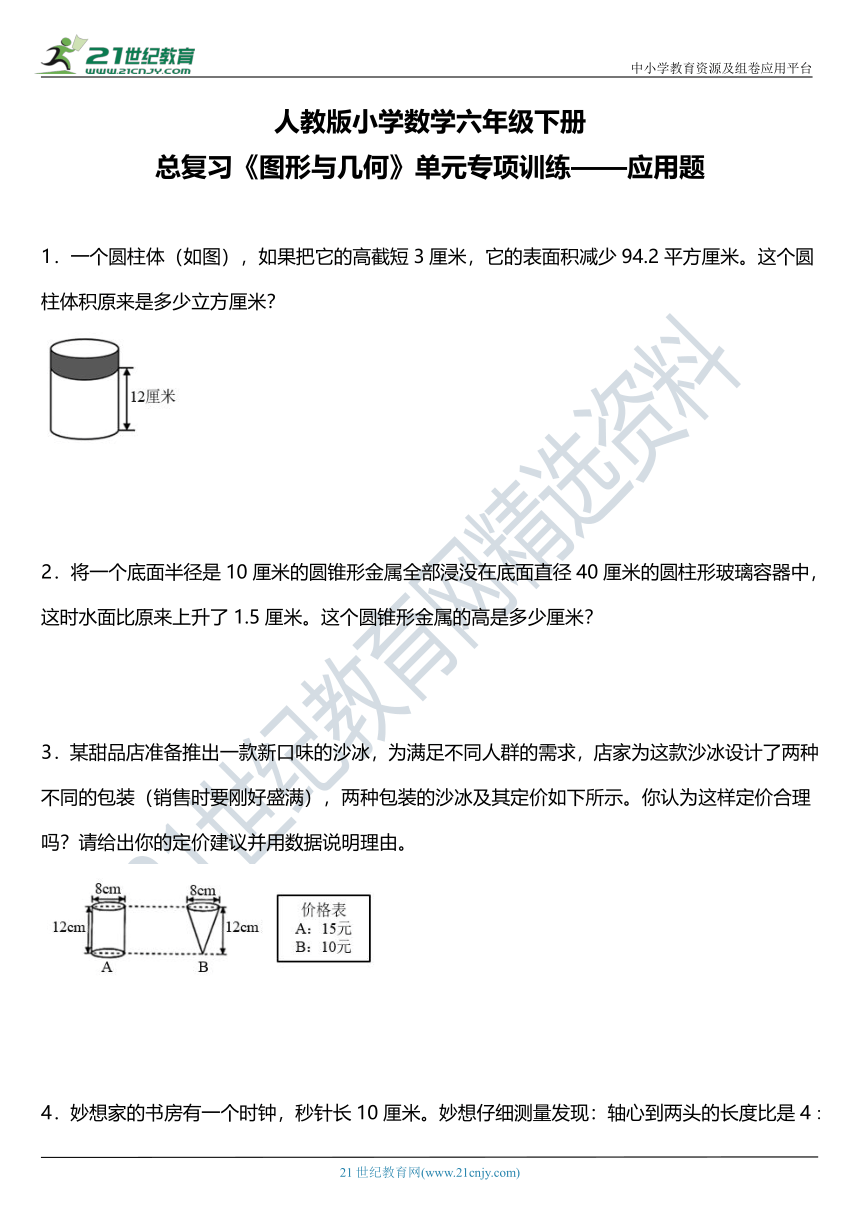 | |
| 格式 | doc | ||
| 文件大小 | 692.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 21:05:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版小学数学六年级下册
总复习《图形与几何》单元专项训练——应用题
1.一个圆柱体(如图),如果把它的高截短3厘米,它的表面积减少94.2平方厘米。这个圆柱体积原来是多少立方厘米?
2.将一个底面半径是10厘米的圆锥形金属全部浸没在底面直径40厘米的圆柱形玻璃容器中,这时水面比原来上升了1.5厘米。这个圆锥形金属的高是多少厘米?
3.某甜品店准备推出一款新口味的沙冰,为满足不同人群的需求,店家为这款沙冰设计了两种不同的包装(销售时要刚好盛满),两种包装的沙冰及其定价如下所示。你认为这样定价合理吗?请给出你的定价建议并用数据说明理由。
4.妙想家的书房有一个时钟,秒针长10厘米。妙想仔细测量发现:轴心到两头的长度比是4∶1。这根秒针的针尖绕轴心转一圈能扫过的面积是多少平方厘米?
5.如图三角形ABC是一个直角三角形,分别以三条边所在的直线为轴旋转得到三个不同的立体形体,这三个立体图形的体积分别是多少立方厘米?
6.一个圆锥形沙堆,底面积是24平方米,高是1.2米,用这堆沙去填一个长7.5米,宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
7.一个无水长方体玻璃缸,长4.8分米,宽2.5分米,高3分米,打开水龙头给玻璃缸注水,从7:00开始注水,7:04关闭水龙头停止注水,水的流量为6立方分米/分,接着在玻璃缸里放入一个长方体铁块,全部浸没水中,玻璃缸的水面高度从注水到放入铁块的变化情况如图所示。
(1)如图中点( )的位置表示停止注水。(从A、B、C中选择)
(2)7:04玻璃缸中水的高度是多少分米?
8.一块圆锥形的橡皮泥,高12厘米,底面直径为4厘米,小芳将它捏成一个高10厘米的圆柱形。圆柱形的底面积是多少平方厘米?(结果保留π)
9.一个压路机的前轮是圆柱形,轮宽1.5米,直径80厘米,每分钟滚动10周,一小时能压多少平方米的路面?
10.如图,有一个装有360毫升饮料的瓶子,瓶中饮料的高度是16厘米。把盖子拧紧后倒置放平,没有饮料的部分是圆柱形,高度是4厘米,这个瓶子的容积是多少毫升?
11.阅读下面材料并解决问题。
水是生命之源,是人类赖以生存的物质基础。党和政府历来把安全饮水列为头等民生大事,集中人力、物力全力保障职工群众的用水需求。但是好多地方每到夏季用水高峰期,出现水压低、水量小的现象,有时侯甚至无水可用,严重影响着居民日常生活。自从开展“我为群众办实事”活动以来,地方政府都积极调研。
一个山区的学校修建一个圆柱形蓄水池,水池的底面直径是8米,深是2.5米。
(1)把水池的内侧壁和底面抹上水泥,抹水泥部分的面积是多少平方米?
(2)这个蓄水池能容纳多少吨水?(1立方米水的质量是1吨)
12.把一个底面半径是4厘米、高是7厘米的圆柱形铁块,重新熔铸成一个底面半径是8厘米的圆锥体,熔转成的圆锥体的高是多少厘米?
13.做一对无盖的圆柱形水桶,每只底面周长都是12.56分米,高都是4分米,至少需铁皮都是平方分米?(得数保留整平方分米)
14.探究与实践。
图1、图2、图3都是我们学过的柱体。
(1)回顾已有知识:
V长方体=( ),V正方体=( ),V圆柱=( )。
(2)发现共同规律:V柱体=( )。
(3)尝试解决问题:
图4是一种酸奶包装盒(单位:厘米),你能计算出这种牛奶盒的容积是多少毫升吗?(厚度忽略不计)
15.有一张长方形的铁皮(如图),剪下图中的阴影部分,正好可以做成一个底面直径为8分米的圆柱形油桶。
(1)原来的长方形铁皮面积是多少平方分米?
(2)做成的这个圆柱形油桶的容积是多少升?
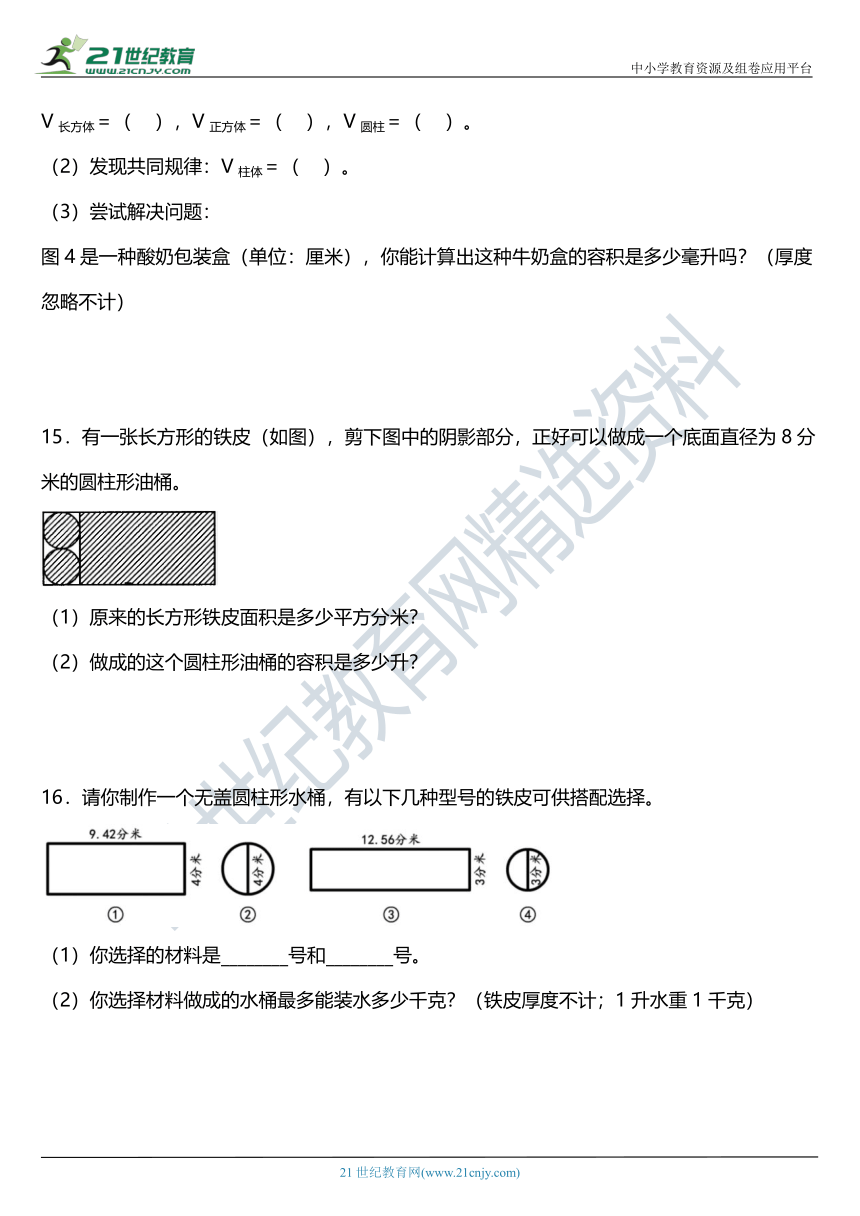
16.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你选择的材料是________号和________号。
(2)你选择材料做成的水桶最多能装水多少千克?(铁皮厚度不计;1升水重1千克)
17.有一个底面直径是20cm的圆柱形容器中装入一些水,把一个底面直径为10cm,高12cm的圆锥形钢锭浸没在水中,容器中的水面会上升多少厘米?
18.有一个长方体的水槽,槽内有一个圆锥形的零件完全浸在水中,已知水槽的长为1米,宽为5分米,水面高0.5米,零件的底面直径为40厘米。当零件从水中取出后,水面下降了6.28厘米,求这个圆锥形零件的高是多少米?
19.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不断追求的航天梦。下面是某运载火箭整流罩的简约示意图,如果忽略厚度,该整流罩的容积是多少?
20.为创建全国文明城市,阳城公园种了一块三角形的草坪,在比例尺1∶8000的平面图上量得这块草坪的底是2.5厘米,高是0.4厘米。这块三角形草地的实际面积是多少?
21.每年的3月22日是世界水日,它的设立目的是唤起公众的节水意识,加强水资源保护。玲玲家做了一个圆柱形铁皮水桶(无盖),这个水桶高6分米,底面半径2分米。做这个水桶至少要用多少铁皮?
22.工地上有一堆圆锥形沙堆,高1.5米,底面直径是6米。
(1)这个沙堆的占地面积是多少?
(2)如果每立方米沙约重1.7吨,这堆沙约重多少吨?
23.一个圆锥形沙堆,底面周长是12.56米,高1.5米,如果每立方米的沙子约重1.6吨,这堆沙子约重多少吨?(得数保留整数)
24.中国航天航空事业的发展日新月异,2023年长征系列运载火箭累计发射次数有望突破500次。小明是个小航天迷,下面是小明制作的火箭模型,请你运用所学的知识求出它的体积。
25.一个直径20厘米的圆柱形玻璃容器里,盛有30厘米高的水,将一个底面半径3厘米、高20厘米的圆锥形铁块,全部浸没在水中。这时玻璃容器中的水高多少厘米?
26.我国古代劳动人民早在2000多年前,就会计算不同形状物体的体积。《九章算术》中记载的圆柱体体积计算方法是“周自相乘,以高乘之,十二而一”,也就是底面周长的平方乘高,再除以12。
(1)想一想,上面的计算方法中,圆周率的取值是 ( )。
(2)如果一个圆柱的底面周长18厘米,高10厘米。你能分别用我们学过的方法和《九章算术》中记载的方法算出圆柱的体积吗(圆周率取近似值3)?
27.有圆柱体与正方体容器各一个。圆柱体的底面直径与正方体的棱长都是4分米。圆柱体里装有2分米高的水,这时水与圆柱体的接触面积是多少平方分米?把圆柱体中的水倒入正方体容器内,这时水面高多少分米?(计算结果保留π)
28.江海农业示范园内有200个蔬菜大棚(如图),每个大棚长15米,横截面是一个直径2米的半圆。
(1)这些大棚的种植面积共有多少平方米?
(2)搭建一个大棚大约要用多少平方米的塑料薄膜?
29.一块圆柱形的橡皮泥,高15厘米,底面直径为4厘米,小芳将它捏成一个高10厘米的长方体。这个长方体的底面积是多少平方厘米?(结果保留π)
30.一个圆锥形沙堆,底面积36平方米,高0.8米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
31.有一个近似圆锥形的稻谷堆,底面直径4米,高是1.2米。如果每立方米的稻谷约重0.5吨,这个稻谷堆大约重多少吨?(得数保留1位小数)
32.一个无盖的圆柱形水桶,高5分米,水桶外围的一圈铁箍大约长12.56分米,做个这个水桶至少要木板多少平方分米?
33.一台压路机的前轮是圆柱形,轮宽1.5米,前轮直径是10分米,前轮转动10周,压过的面积是多少平方分米?
34.小明家去年秋季收获的稻谷堆成圆锥形,高是1.5米,底面直径是4米。
(1)这堆稻谷的体积是多少?
(2)如果每立方米稻谷重650千克,这堆稻谷重多少千克?
(3)如果小明家去年收割的稻谷面积是有0.4公顷,那么平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价为2.8元,这些稻谷能卖多少钱?
35.居民小区的健身设施需要定期进行维护和修缮,李师傅运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是12.56米,高3米。
(1)这些沙子的体积是多大?
(2)沙坑的长度10米,宽6.28米,需要填沙子的厚度是20厘米,这些沙子够用吗?
参考答案:
1.1177.5立方厘米
【分析】表面积减少的侧面积,减少的侧面积÷截短的高=圆柱底面周长,底面周长÷π÷2=底面半径,再根据圆柱体积=底面积×高,求出原来体积即可。
【详解】94.2÷3=31.4(厘米)
31.4÷3.14÷2=5(厘米)
3.14×52×(12+3)
=3.14×25×15
=1177.5(立方厘米)
答:这个圆柱体积原来是1177.5立方厘米。
【点睛】关键是掌握并灵活运用圆柱侧面积和体积公式。
2.18厘米
【分析】水面上升的体积就是圆锥形铁块体积,根据圆柱体积公式,用容器底面积×上升的水的高度,即可求出铁块体积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】3.14×(40÷2)2(3.14×102)
=3.14×400×1.5×3÷(3.14×100)
=1256×1.5×3÷314
=1884×3÷314
=5652÷314
=18(厘米)
答:这个圆锥形金属的高是18厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
3.不合理;理由见详解
【分析】因为等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的价格应当是圆锥的3倍,由此即可解答。
【详解】3.14×(8÷2)2×12
=3.14×42×12
=3.14×16×12
=602.88(立方厘米)
602.88×=200.96(立方厘米)
602.88÷200.96=3
所以A包装的沙冰价格也应该是B包装的沙冰价格的3倍。
15÷10=1.5
现在的A包装的沙冰价格是B包装的沙冰价格的1.5倍,现在这样定价不合理。
15÷3=5(元)
10×3=30(元)
答:我认为这样定价不合理,A包装的价钱应当是B包装的3倍;定价建议如下:如果A包装定价为15元,则B包装定价5元,如果B包装定价为10元,则A包装定价为30元。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
4.200.96平方厘米
【分析】根据题干可知,轴心到两头的长度比是4∶1。把秒针平均分成5份,轴心到针尾的距离占1份是2厘米,轴心到针尖距离占4份是8厘米,这根秒针扫过的面积等于半径为8厘米的圆的面积,根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据代入公式解答。
【详解】3.14×(10×)2
=3.14×82
=3.14×64
=200.96(平方厘米)
答:这根秒针的针尖绕轴心转一圈能扫过的面积是200.96平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式的灵活运用。
5.37680立方厘米;50240立方厘米;30144立方厘米
【分析】将直角三角形以AB为轴为轴旋转,得到一个高为40厘米,底面半径为30厘米的圆锥,再利用圆锥的体积公式代入数据解答;
以BC为轴旋转,得到一个高为30厘米,底面半径为40厘米的圆锥,再利用圆锥的体积公式代入数据解答;
以AC为轴旋转,得到两个圆锥,借助三角形的面积公式,列式30×40÷2,求出三角形的面积是600平方厘米,再用600×2÷50求出斜边上的高为24厘米,即底面半径为24厘米,两个圆锥的高之和是50厘米,先求出底面积,进而求出两个圆锥的体积即可。
【详解】以AB为轴旋转的圆锥:
×3.14×302×40
=×3.14×900×40
=942×40
=37680(立方厘米)
以BC为轴旋转的圆锥:
×3.14×402×30
=×30×3.14×1600
=31.4×1600
=50240(立方厘米)
以AC为轴旋转的立体图形,两个圆锥半径:
30×40÷2=600(平方厘米)
600×2÷50=24(厘米)
体积:×3.14×242×50
=×3.14×576×50
=602.88×50
=30144(立方厘米)
答:以AB为轴旋转的圆锥体积37680立方厘米;以BC为轴旋转的圆锥体积50240立方厘米;以AC为轴旋转的立体图形体积是30144立方厘米。
【点睛】掌握圆锥的特征和圆锥的体积计算公式是解答题目的关键。
6.32厘米
【分析】根据题意可知把圆锥形的沙堆填在长方体沙坑里,沙的体积不变,根据圆锥的体积公式:V,求出沙的体积,然后用沙的体积除以长方体沙坑的底面积即可。据此解答。
【详解】24×1.2×÷(7.5×4)
=28.8×÷30
=9.6÷30
=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
【点睛】熟练掌握和灵活运用圆锥的体积公式、长方体的体积公式是解答本题的关键。
7.(1)B
(2)2分米
【分析】(1)因为注水速度一定,所以水面高度与注水时间成正比例,正比例的图像是一条过原点的直线。由此可知,从注水7:00开始到7:04,这段时间是注水时间,是条直线,根据图形可知,点B的位置表示停止注水,据此解答。
(2)先用每分钟水的流量×注水到关闭水龙头的时间,求出注入的水的体积,再根据长方体体积公式:体积=底面积×高;高=体积÷底面积,即可解答。
【详解】(1)根据分析可知,图中点B的位置表示停止注水。
(2)7时4分-7时=4分
6×4=24(立方分米)
24÷(4.8×2.5)
=24÷12
=2(分米)
答:玻璃缸中水的高度是2分米。
【点睛】本题考查了利用正比例图像及长方体体积公式解决问题,需熟练掌握正比例图像特点,灵活使用长方体体积公式。
8.1.6π平方厘米
【分析】根据体积的意义可知,把这块橡皮泥无论捏成什么形状,体积不变。根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】π×(4÷2)2×12÷10
π×4×12÷10
=16π÷10
=1.6π(平方厘米)
答:圆柱形的底面积是1.6π平方厘米。
【点睛】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
9.2260.8平方米
【分析】80厘米=0.8米,先根据圆柱的侧面积公式:S=πdh,用3.14×0.8×1.5即可求出滚动1周压过的面积,已知每分钟滚动10周,则用3.14×0.8×1.5×10×60即可求出一小时能压多少平方米的路面。
【详解】80厘米=0.8米
1小时=60分
3.14×0.8×1.5×10×60
=3.768×10×60
=2260.8(平方米)
答:一小时能压2260.8平方米的路面。
【点睛】本题考查了圆柱的侧面积公式的灵活应用。
10.450毫升
【分析】根据题意,先用体积360毫升除以高16厘米求出瓶子的底面积,瓶子的容积=饮料的体积+倒放时空余部分的体积,瓶子的容积也就是求高为(16+4)厘米的圆柱的容积;根据圆柱的体积(容积)公式:V=Sh,代入数据计算即可。
【详解】360÷16×(16+4)
=22.5×20
=450(毫升)
答:这个瓶子的容积是450毫升。
【点睛】解决此题的关键是理解前后两次瓶子的放置,后面空余部分的体积就是前面空余部分的体积。
11.(1)113.04平方米
(2)125.6吨
【分析】(1)由于蓄水池无盖,所以抹水泥部分是这个圆柱的侧面和一个底面,根据圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
(2)根据圆柱的体积公式:V=πr2h,把数据代入公式求出水的体积,然后用水的体积乘每立方米水的质量即可。
【详解】(1)3.14×8×2.5+3.14×(8÷2)2
=25.12×2.5+3.14×16
=62.8+50.24
=113.04(平方米)
答:抹水泥部分的面积是113.04平方米。
(2)3.14×(8÷2)2×2.5×1
=3.14×16×2.5×1
=50.24×2.5×1
=125.6×1
=125.6(吨)
答:这个蓄水池能容纳125.6吨水。
【点睛】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是熟记公式。
12.5.25厘米
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,那么h=V÷÷πr2,把数据代入公式解答。
【详解】3.14×42×7÷÷(3.14×82)
=3.14×16×7÷÷(3.14×64)
=351.68×3÷200.96
=1055.04÷200.96
=5.25(厘米)
答:熔转成的圆锥体的高是5.25厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
13.126平方分米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆柱形水桶的底面半径;因为是无盖,再根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,求出一个水桶需要的铁皮,再乘2,即可解答。
【详解】12.56÷3.14÷2
=4÷2
=2(分米)
(3.14×22+3.14×2×2×4)×2
=(3.14×4+6.28×2×4)×2
=(12.56+12.56×4)×2
=(12.56+50.24)×2
=62.8×2
=125.6
≈126(平方分米)
答:至少需铁皮126平方分米。
【点睛】熟练掌握圆柱的表面积公式是解答本题的关键。
14.(1)abh;a3;Sh;(2)Sh;(3)450毫升
【分析】(1)根据长方体体积公式:长方体的体积=长×宽×高,正方体的体积公式:正方体的体积=棱长×棱长×棱长,圆柱的体积公式:圆柱的体积=底面积×高,据此解答;
(2)因为长方体的底面积=长×宽,正方体的底面积=棱长×棱长,据此可知,柱体的体积=底面积×高,据此解答;
(3)观察发现,底面是一个梯形,根据梯形的面积公式求出底面积,然后再乘高,即可求出牛奶的容积。
【详解】(1)V长方体=abh
V正方体=a3
V圆柱=Sh
(2)发现共同规律:V柱体=Sh
(3)(5+10)×6÷2
=15×6÷2
=45(平方厘米)
45×10=450(立方厘米)
450立方厘米=450毫升
答:这种牛奶盒的容积是450毫升。
【点睛】本题主要考查了圆柱的体积公式、长方体的体积公式、正方体的体积公式的灵活应用。
15.(1)529.92平方分米;(2)803.84升
【分析】(1)观察题意可知,长方形的宽是2个底面直径,长方形的长是一个底面直径和一个底面周长的和,已知底面直径为8分米,根据底面周长公式:C=πd,用2×8即可求出长方形的宽,用8+3.14×8即可求出长方形的长,然后根据长方形的面积公式,求出原来的长方形铁皮面积;
(2)观察题意可知圆柱的底面直径是8分米,高是(8×2)分米,根据圆柱的体积公式,代入数据解答即可。
【详解】(1)2×8=16(分米)
8+3.14×8
=8+25.12
=33.12(分米)
16×33.12=529.92(平方分米)
答:原来的长方形铁皮面积是529.92平方分米。
(2)3.14×(8÷2)2×8×2
=3.14×42×8×2
=3.14×16×8×2
=803.84(立方分米)
803.84立方分米=803.84升
答:做成的这个圆柱形油桶的容积是803.84升。
【点睛】本题考查了长方形和圆柱展开图之间的关系、长方形面积公式和圆柱体积公式的灵活应用。
16.(1)①④或②③
(2)选择①④:28.26千克
选择②③:37.68千克
【分析】(1)根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开后是一个长方形,这个长方形的长等于圆柱的底面周长,这个长方形的宽等于圆柱的高。由此可知,有两种不同的选择,可以选①和④,也可以选②和③,据此解答。
(2)根据圆柱的容积(体积)公式:,把数据代入公式求出这个圆柱形水桶的容积,然后再乘每升水的质量即可。
【详解】(1)①④或②③
(2))选择①④:
=3.14××4
=3.14×2.25×4
=7.065×4
=28.26(立方分米)
28.26立方分米=28.26升=28.26千克
答:最多能装水28.26千克。
选择②③:
=3.14××3
=3.14×4×3
=12.56×3
=37.68(立方分米)
37.68立方分米=37.68升=37.68千克
答:最多能装水37.68千克。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆柱的容积(体积)公式及应用,关键是熟记公式。
17.1厘米
【分析】水面上升的体积=圆锥体积,根据圆锥体积=底面积×高÷3,求出圆锥形钢锭体积,钢锭体积÷圆柱形容器底面积=水面上升的高度,据此列式解答。
【详解】3.14××12÷3÷[3.14×]
=3.14×52×12÷3÷[3.14×102]
=3.14×25×12÷3÷[3.14×100]
=314÷314
=1(厘米)
答:容器中的水面会上升1厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
18.0.75米
【分析】水面下降的体积就是圆锥体积,水槽长×宽×水面下降的高度=圆锥体积,根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】5分米=0.5米、6.28厘米=0.0628米、40厘米=0.4米
1×0.5×0.0628=0.0314(立方米)
0.0314×3÷[3.14×(0.4÷2)2]
=0.0942÷[3.14×0.22]
=0.0942÷[3.14×0.04]
=0.0942÷0.1256
=0.75(米)
答:这个圆锥形零件的高是0.75米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式,利用转化思想,先求出圆锥体积。
19.150.72立方米
【分析】该图形的容积等于下方圆柱的容积加上上方圆锥的容积,根据圆柱的容积公式:V=πr2h,圆锥的容积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(4÷2)2×10+×3.14×(4÷2)2×(16-10)
=3.14×4×10+×3.14×4×6
=125.6+25.12
=150.72(立方米)
答:该整流罩的容积是150.72立方米。
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
20.3200平方米
【分析】根据实际距离=图上距离÷比例尺,据此求出这块草坪的底和高的实际长度,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】2.5÷=20000(厘米)=200(米)
0.4÷=3200(厘米)=32(米)
200×32÷2
=6400÷2
=3200(平方米)
答:这块三角形草地的实际面积是3200平方米。
【点睛】本题考查比例尺,结合三角形的面积的计算方法是解题的关键。
21.87.92平方分米
【分析】“”求需要铁皮的面积就是求圆柱的表面积,因为这个圆柱形水桶无盖,所以只计算圆柱的侧面积和一个底面积,据此解答。
【详解】2×3.14×2×6+3.14×22
=6.28×2×6+12.56
=12.56×6+12.56
=75.36+12.56
=87.92(平方分米)
答:做这个水桶至少要用87.92平方分米铁皮。
【点睛】本题主要考查圆柱表面积公式的应用,明确需要去掉一个圆柱的底面积是解答题目的关键。
22.(1)28.26平方米;
(2)24.021吨
【分析】(1)求这个沙堆的占地面积,实际上是求圆锥的底面积,根据圆的面积公式S=代入数据即可得解。
(2)利用圆锥的体积公式:V=,代入数据求出圆锥形沙堆的体积,再乘每立方米沙堆的重量,即可求出这堆沙大概的重量。
【详解】(1)3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26(平方米)
答:这个沙堆的占地面积是28.26平方米。
(2)28.26×1.5×1.7
=9.42×1.5×1.7
=14.13×1.7
=24.021(吨)
答:这堆沙约重24.021吨。
【点睛】此题的解题关键是灵活运用圆锥的底面积以及圆锥的体积公式求解。
23.10吨
【分析】首先根据底面周长是12.56m,求出圆锥的底面半径,再根据圆锥的体积公式:V=sh,求出沙堆的体积,然后用沙的体积乘每立方米沙的质量即可。
【详解】12.56÷3.14÷2
=4÷2
=2(米)
×3.14×22×1.5
=×(3.14×4×1.5)
=×(12.56×1.5)
=×18.84
=6.28(立方米)
6.28×1.6≈10(吨)
答:这堆沙子约重10吨。
【点睛】此题主要考查圆锥的体积公式在实际生活中的应用,掌握圆锥的体积计算公式是解答本题的关键。
24.1884立方厘米
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,用3.14×(10÷2)2×20即可求出圆柱的体积,用3.14×(10÷2)2×12×即可求出圆锥的体积,最后把两部分相加即可。
【详解】3.14×(10÷2)2×20
=3.14×52×20
=3.14×25×20
=1570(立方厘米)
3.14×(10÷2)2×12×
=3.14×52×12×
=3.14×25×12×
=314(立方厘米)
1570+314=1884(立方厘米)
答:火箭模型1884立方厘米。
【点睛】本题主要考查了圆柱体积公式和圆锥体积公式的应用。
25.30.6厘米
【分析】将圆锥浸没在水中后,水面上升部分的体积和圆锥的体积相等。圆锥体积=底面积×高÷3,圆柱体积=底面积×高。据此,先求出圆锥的体积,再将圆锥的体积除以圆柱的底面积,求出水面上升了多少,最后利用加法求出这时玻璃容器中的水高。
【详解】20÷2=10(厘米)
3.14×32×20÷3÷(3.14×102)
=188.4÷314
=0.6(厘米)
30+0.6=30.6(厘米)
答:这时玻璃容器中的水高30.6厘米。
【点睛】本题考查了圆柱和圆锥的体积,灵活运用圆柱和圆锥的体积公式是解题的关键。
26.(1)3
(2)见详解
【分析】(1)根据题干描述,古代的圆柱体积计算方法为:V=C2×h÷12,现在方法是V=Sh,通过化简即可得出圆周率的取值;
(2)现在的方法:圆柱的体积公式V=Sh,先算出底面圆的半径,再把数据代入公式,即可得出答案。
古人的方法:根据题干描述,古代的圆柱体积计算方法为:V=C2×h÷12,将数据代入公式,即可得出答案。
【详解】(1)C2×h÷12=Sh
(2r)2×h÷12=r2×h
=3
圆周率的取值是3。
(2)方法1:(18÷3÷2)2×3×10
=9×3×10
=270(立方厘米)
方法2:18×18×10÷12
=3240÷12
=270(立方厘米)
答:圆柱的体积是270立方厘米。
【点睛】本题考查学生对现代和古人求圆柱体积方法的掌握和运用,本题要注意π的取值为3。
27.12π平方分米;0.5π分米。
【分析】因为水与圆柱体的容器的接触面只有侧面和底面,根据圆柱的表面积公式S=侧面积+底面积,将数据代入即可得出答案。
把圆柱体中的水倒入正方体容器内,水的体积不变,根据圆柱的体积公式V=Sh,先求出水的体积,再根据h=V÷S(正方形面积公式S=棱长×棱长),将数据代入,即可得出水面高度
【详解】4π×2+(4÷2)2×π
=8π+22×π
=8π+4π
=12π(平方分米)
(4÷2)2×π×2÷(4×4)
=22×π×2÷16
=8π÷16
=0.5π(分米)
答:水与圆柱体的接触面积是12平方分米,水面高0.5π分米。
【点睛】本题考查学生对圆柱表面公式和圆柱体积公式的掌握和运用,解答时要注意水从圆柱体中倒入正方体容器内,水的体积不变。
28.(1)6000平方米
(2)50.24平方米
【分析】(1)先求出一个大棚的占地面积,利用长方形的面积S=长×宽即可求出一个大棚的占地面积,再乘大棚的数量;
(2)求搭建一个大棚大约要用多少平方米的塑料薄膜就是求半个圆柱的侧面积和一个底面积的和,利用公式S=πr2+πdh÷2即可。
【详解】(1)2×15×200
=30×200
=6000(平方米)
答:这些大棚的种植面积共有6000平方米。
(2)3.14×(2÷2)2+3.14×2×15÷2
=3.14×1+6.28×15÷2
=3.14+94.2÷2
=3.14+47.1
=50.24(平方米)
答:搭建一个大棚大约要用50.24平方米的塑料薄膜。
【点睛】本题考查了圆柱的侧面积计算公式的应用。
29.6π平方厘米
【分析】先根据圆柱的体积公式(V=πr2h)先算出圆柱形橡皮泥的体积,再根据橡皮泥体积不变,利用长方体体积公式(V=abh)即可求出长方体的底面积是多少平方厘米。
【详解】(4÷2)2×15×π
=4×15×π
=60π(立方厘米)
60π÷10=6π(平方厘米)
答:这个长方体的底面积是6π平方厘米。
【点睛】此题主要考查长方体和圆柱体的体积计算方法,关键是明白橡皮泥的体积不变。
30.32厘米
【分析】根据题意可知把圆锥形的沙堆填在长方体沙坑里,沙的体积不变,根据圆锥的体积公式:VSh,求出沙的体积,然后用沙的体积除以长方体沙坑的底面积即可,据此解答。
【详解】36×0.8÷(7.5×4)
=12×0.8÷30
=9.6÷30
=0.32(米)
=32(厘米)
答:沙坑里沙子的厚度是32厘米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用。
31.2.5吨
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形稻谷的体积,再用圆锥稻谷的体积×0.5,即可解答。
【详解】3.14×(4÷2)2×1.2××0.5
=3.14×4×1.2××0.5
=12.56×1.2××0.5
=15.072××0.5
=5.024×0.5
=2.512
≈2.5(吨)
答:这个稻谷堆大约2.5吨。
【点睛】熟练掌握圆锥的体积公式是解答本题的关键。
32.75.36平方分米
【分析】根据题意,水桶外围一圈的长度就是这个圆柱形水桶的底面周长,根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出底面半径;求这个水桶至少要木板多少平方分米,就是求这个水桶的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(12.56÷3.14÷2)2+12.56×5
=3.14×(4÷2)2+62.8
=3.14×4+62.8
=12.56+62.8
=75.36(平方分米)
答:做这个水桶至少要木板75.36平方分米。
【点睛】本题考查圆柱的表面积公式的应用,注意这个无盖圆柱形水桶的表面积是一个底面积与侧面积的和。
33.4710平方分米
【分析】压路机的前轮滚动一周压过的面积就是圆柱形前轮的侧面积,根据侧面积=πdh求出侧面积,再乘上10就是前轮转动10周压过的面积,据此解答即可。
【详解】1.5米=15分米
3.14×10×15×10
=31.4×15×10
=471×10
=4710(平方分米)
答:压过的面积是4710平方分米。
【点睛】此题主要考查圆柱侧面积公式的灵活运用,关键是熟记公式。
34.(1)6.28立方米;
(2)4082千克;
(3)10205千克;
(4)11429.6元
【分析】(1)根据圆锥的体积公式:V=πr2h,据此计算出这堆稻谷的体积;
(2)用稻谷的体积乘每立方米稻谷的重量即可求解;
(3)用稻谷的重量除以稻谷的面积即可;
(4)根据单价×数量=总价,用稻谷的重量乘2.8即可求解。
【详解】(1)×3.14×(4÷2)2×1.5
=×3.14×4×1.5
=×3.14×(4×1.5)
=×3.14×6
=×6×3.14
=2×3.14
=6.28(立方米)
答:这堆稻谷的体积是6.28立方米。
(2)6.28×650=4082(千克)
答:这堆稻谷重4082千克。
(3)4082÷0.4=10205(千克)
答:平均每公顷产稻谷10205千克。
(4)4082×2.8=11429.6(元)
答:这些稻谷能卖11429.6元。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
35.(1)12.56立方米
(2)够用
【分析】(1)已知圆锥形沙堆的底面周长,根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆锥形沙堆的底面半径;然后根据圆锥的体积公式V=πr2h,代入数据计算,即可求出这些沙子的体积。
(2)根据长方体的体积公式V=abh,求出长方体沙坑需要沙子的体积,再与上一题的沙子体积比较,得出结论。注意单位的换算:1米=100厘米。
【详解】(1)圆锥的底面半径:
12.56÷3.14÷2
=4÷2
=2(米)
圆锥的体积:
×3.14×22×3
=×3.14×4×3
=12.56(立方米)
答:这些沙子的体积是12.56立方米。
(2)20厘米=0.2米
10×6.28×0.2
=62.8×0.2
=12.56(立方米)
答:这些沙子够用。
【点睛】本题考查圆锥底面周长、圆锥体积、长方体体积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版小学数学六年级下册
总复习《图形与几何》单元专项训练——应用题
1.一个圆柱体(如图),如果把它的高截短3厘米,它的表面积减少94.2平方厘米。这个圆柱体积原来是多少立方厘米?
2.将一个底面半径是10厘米的圆锥形金属全部浸没在底面直径40厘米的圆柱形玻璃容器中,这时水面比原来上升了1.5厘米。这个圆锥形金属的高是多少厘米?
3.某甜品店准备推出一款新口味的沙冰,为满足不同人群的需求,店家为这款沙冰设计了两种不同的包装(销售时要刚好盛满),两种包装的沙冰及其定价如下所示。你认为这样定价合理吗?请给出你的定价建议并用数据说明理由。
4.妙想家的书房有一个时钟,秒针长10厘米。妙想仔细测量发现:轴心到两头的长度比是4∶1。这根秒针的针尖绕轴心转一圈能扫过的面积是多少平方厘米?
5.如图三角形ABC是一个直角三角形,分别以三条边所在的直线为轴旋转得到三个不同的立体形体,这三个立体图形的体积分别是多少立方厘米?
6.一个圆锥形沙堆,底面积是24平方米,高是1.2米,用这堆沙去填一个长7.5米,宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
7.一个无水长方体玻璃缸,长4.8分米,宽2.5分米,高3分米,打开水龙头给玻璃缸注水,从7:00开始注水,7:04关闭水龙头停止注水,水的流量为6立方分米/分,接着在玻璃缸里放入一个长方体铁块,全部浸没水中,玻璃缸的水面高度从注水到放入铁块的变化情况如图所示。
(1)如图中点( )的位置表示停止注水。(从A、B、C中选择)
(2)7:04玻璃缸中水的高度是多少分米?
8.一块圆锥形的橡皮泥,高12厘米,底面直径为4厘米,小芳将它捏成一个高10厘米的圆柱形。圆柱形的底面积是多少平方厘米?(结果保留π)
9.一个压路机的前轮是圆柱形,轮宽1.5米,直径80厘米,每分钟滚动10周,一小时能压多少平方米的路面?
10.如图,有一个装有360毫升饮料的瓶子,瓶中饮料的高度是16厘米。把盖子拧紧后倒置放平,没有饮料的部分是圆柱形,高度是4厘米,这个瓶子的容积是多少毫升?
11.阅读下面材料并解决问题。
水是生命之源,是人类赖以生存的物质基础。党和政府历来把安全饮水列为头等民生大事,集中人力、物力全力保障职工群众的用水需求。但是好多地方每到夏季用水高峰期,出现水压低、水量小的现象,有时侯甚至无水可用,严重影响着居民日常生活。自从开展“我为群众办实事”活动以来,地方政府都积极调研。
一个山区的学校修建一个圆柱形蓄水池,水池的底面直径是8米,深是2.5米。
(1)把水池的内侧壁和底面抹上水泥,抹水泥部分的面积是多少平方米?
(2)这个蓄水池能容纳多少吨水?(1立方米水的质量是1吨)
12.把一个底面半径是4厘米、高是7厘米的圆柱形铁块,重新熔铸成一个底面半径是8厘米的圆锥体,熔转成的圆锥体的高是多少厘米?
13.做一对无盖的圆柱形水桶,每只底面周长都是12.56分米,高都是4分米,至少需铁皮都是平方分米?(得数保留整平方分米)
14.探究与实践。
图1、图2、图3都是我们学过的柱体。
(1)回顾已有知识:
V长方体=( ),V正方体=( ),V圆柱=( )。
(2)发现共同规律:V柱体=( )。
(3)尝试解决问题:
图4是一种酸奶包装盒(单位:厘米),你能计算出这种牛奶盒的容积是多少毫升吗?(厚度忽略不计)
15.有一张长方形的铁皮(如图),剪下图中的阴影部分,正好可以做成一个底面直径为8分米的圆柱形油桶。
(1)原来的长方形铁皮面积是多少平方分米?
(2)做成的这个圆柱形油桶的容积是多少升?
16.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你选择的材料是________号和________号。
(2)你选择材料做成的水桶最多能装水多少千克?(铁皮厚度不计;1升水重1千克)
17.有一个底面直径是20cm的圆柱形容器中装入一些水,把一个底面直径为10cm,高12cm的圆锥形钢锭浸没在水中,容器中的水面会上升多少厘米?
18.有一个长方体的水槽,槽内有一个圆锥形的零件完全浸在水中,已知水槽的长为1米,宽为5分米,水面高0.5米,零件的底面直径为40厘米。当零件从水中取出后,水面下降了6.28厘米,求这个圆锥形零件的高是多少米?
19.探索浩瀚宇宙,发展航天事业,建设航天强国,是我国不断追求的航天梦。下面是某运载火箭整流罩的简约示意图,如果忽略厚度,该整流罩的容积是多少?
20.为创建全国文明城市,阳城公园种了一块三角形的草坪,在比例尺1∶8000的平面图上量得这块草坪的底是2.5厘米,高是0.4厘米。这块三角形草地的实际面积是多少?
21.每年的3月22日是世界水日,它的设立目的是唤起公众的节水意识,加强水资源保护。玲玲家做了一个圆柱形铁皮水桶(无盖),这个水桶高6分米,底面半径2分米。做这个水桶至少要用多少铁皮?
22.工地上有一堆圆锥形沙堆,高1.5米,底面直径是6米。
(1)这个沙堆的占地面积是多少?
(2)如果每立方米沙约重1.7吨,这堆沙约重多少吨?
23.一个圆锥形沙堆,底面周长是12.56米,高1.5米,如果每立方米的沙子约重1.6吨,这堆沙子约重多少吨?(得数保留整数)
24.中国航天航空事业的发展日新月异,2023年长征系列运载火箭累计发射次数有望突破500次。小明是个小航天迷,下面是小明制作的火箭模型,请你运用所学的知识求出它的体积。
25.一个直径20厘米的圆柱形玻璃容器里,盛有30厘米高的水,将一个底面半径3厘米、高20厘米的圆锥形铁块,全部浸没在水中。这时玻璃容器中的水高多少厘米?
26.我国古代劳动人民早在2000多年前,就会计算不同形状物体的体积。《九章算术》中记载的圆柱体体积计算方法是“周自相乘,以高乘之,十二而一”,也就是底面周长的平方乘高,再除以12。
(1)想一想,上面的计算方法中,圆周率的取值是 ( )。
(2)如果一个圆柱的底面周长18厘米,高10厘米。你能分别用我们学过的方法和《九章算术》中记载的方法算出圆柱的体积吗(圆周率取近似值3)?
27.有圆柱体与正方体容器各一个。圆柱体的底面直径与正方体的棱长都是4分米。圆柱体里装有2分米高的水,这时水与圆柱体的接触面积是多少平方分米?把圆柱体中的水倒入正方体容器内,这时水面高多少分米?(计算结果保留π)
28.江海农业示范园内有200个蔬菜大棚(如图),每个大棚长15米,横截面是一个直径2米的半圆。
(1)这些大棚的种植面积共有多少平方米?
(2)搭建一个大棚大约要用多少平方米的塑料薄膜?
29.一块圆柱形的橡皮泥,高15厘米,底面直径为4厘米,小芳将它捏成一个高10厘米的长方体。这个长方体的底面积是多少平方厘米?(结果保留π)
30.一个圆锥形沙堆,底面积36平方米,高0.8米。用这堆沙子去填一个长7.5米、宽4米的长方体沙坑,沙坑里沙子的厚度是多少厘米?
31.有一个近似圆锥形的稻谷堆,底面直径4米,高是1.2米。如果每立方米的稻谷约重0.5吨,这个稻谷堆大约重多少吨?(得数保留1位小数)
32.一个无盖的圆柱形水桶,高5分米,水桶外围的一圈铁箍大约长12.56分米,做个这个水桶至少要木板多少平方分米?
33.一台压路机的前轮是圆柱形,轮宽1.5米,前轮直径是10分米,前轮转动10周,压过的面积是多少平方分米?
34.小明家去年秋季收获的稻谷堆成圆锥形,高是1.5米,底面直径是4米。
(1)这堆稻谷的体积是多少?
(2)如果每立方米稻谷重650千克,这堆稻谷重多少千克?
(3)如果小明家去年收割的稻谷面积是有0.4公顷,那么平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价为2.8元,这些稻谷能卖多少钱?
35.居民小区的健身设施需要定期进行维护和修缮,李师傅运来一车沙子要用来维护小区的一个沙坑。这些沙子堆成了一个圆锥形,量得底面周长是12.56米,高3米。
(1)这些沙子的体积是多大?
(2)沙坑的长度10米,宽6.28米,需要填沙子的厚度是20厘米,这些沙子够用吗?
参考答案:
1.1177.5立方厘米
【分析】表面积减少的侧面积,减少的侧面积÷截短的高=圆柱底面周长,底面周长÷π÷2=底面半径,再根据圆柱体积=底面积×高,求出原来体积即可。
【详解】94.2÷3=31.4(厘米)
31.4÷3.14÷2=5(厘米)
3.14×52×(12+3)
=3.14×25×15
=1177.5(立方厘米)
答:这个圆柱体积原来是1177.5立方厘米。
【点睛】关键是掌握并灵活运用圆柱侧面积和体积公式。
2.18厘米
【分析】水面上升的体积就是圆锥形铁块体积,根据圆柱体积公式,用容器底面积×上升的水的高度,即可求出铁块体积,再根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】3.14×(40÷2)2(3.14×102)
=3.14×400×1.5×3÷(3.14×100)
=1256×1.5×3÷314
=1884×3÷314
=5652÷314
=18(厘米)
答:这个圆锥形金属的高是18厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
3.不合理;理由见详解
【分析】因为等底等高的圆柱的体积是圆锥的体积的3倍,所以等底等高的圆柱的价格应当是圆锥的3倍,由此即可解答。
【详解】3.14×(8÷2)2×12
=3.14×42×12
=3.14×16×12
=602.88(立方厘米)
602.88×=200.96(立方厘米)
602.88÷200.96=3
所以A包装的沙冰价格也应该是B包装的沙冰价格的3倍。
15÷10=1.5
现在的A包装的沙冰价格是B包装的沙冰价格的1.5倍,现在这样定价不合理。
15÷3=5(元)
10×3=30(元)
答:我认为这样定价不合理,A包装的价钱应当是B包装的3倍;定价建议如下:如果A包装定价为15元,则B包装定价5元,如果B包装定价为10元,则A包装定价为30元。
【点睛】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
4.200.96平方厘米
【分析】根据题干可知,轴心到两头的长度比是4∶1。把秒针平均分成5份,轴心到针尾的距离占1份是2厘米,轴心到针尖距离占4份是8厘米,这根秒针扫过的面积等于半径为8厘米的圆的面积,根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据代入公式解答。
【详解】3.14×(10×)2
=3.14×82
=3.14×64
=200.96(平方厘米)
答:这根秒针的针尖绕轴心转一圈能扫过的面积是200.96平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式的灵活运用。
5.37680立方厘米;50240立方厘米;30144立方厘米
【分析】将直角三角形以AB为轴为轴旋转,得到一个高为40厘米,底面半径为30厘米的圆锥,再利用圆锥的体积公式代入数据解答;
以BC为轴旋转,得到一个高为30厘米,底面半径为40厘米的圆锥,再利用圆锥的体积公式代入数据解答;
以AC为轴旋转,得到两个圆锥,借助三角形的面积公式,列式30×40÷2,求出三角形的面积是600平方厘米,再用600×2÷50求出斜边上的高为24厘米,即底面半径为24厘米,两个圆锥的高之和是50厘米,先求出底面积,进而求出两个圆锥的体积即可。
【详解】以AB为轴旋转的圆锥:
×3.14×302×40
=×3.14×900×40
=942×40
=37680(立方厘米)
以BC为轴旋转的圆锥:
×3.14×402×30
=×30×3.14×1600
=31.4×1600
=50240(立方厘米)
以AC为轴旋转的立体图形,两个圆锥半径:
30×40÷2=600(平方厘米)
600×2÷50=24(厘米)
体积:×3.14×242×50
=×3.14×576×50
=602.88×50
=30144(立方厘米)
答:以AB为轴旋转的圆锥体积37680立方厘米;以BC为轴旋转的圆锥体积50240立方厘米;以AC为轴旋转的立体图形体积是30144立方厘米。
【点睛】掌握圆锥的特征和圆锥的体积计算公式是解答题目的关键。
6.32厘米
【分析】根据题意可知把圆锥形的沙堆填在长方体沙坑里,沙的体积不变,根据圆锥的体积公式:V,求出沙的体积,然后用沙的体积除以长方体沙坑的底面积即可。据此解答。
【详解】24×1.2×÷(7.5×4)
=28.8×÷30
=9.6÷30
=0.32(米)
0.32米=32厘米
答:沙坑里沙子的厚度是32厘米。
【点睛】熟练掌握和灵活运用圆锥的体积公式、长方体的体积公式是解答本题的关键。
7.(1)B
(2)2分米
【分析】(1)因为注水速度一定,所以水面高度与注水时间成正比例,正比例的图像是一条过原点的直线。由此可知,从注水7:00开始到7:04,这段时间是注水时间,是条直线,根据图形可知,点B的位置表示停止注水,据此解答。
(2)先用每分钟水的流量×注水到关闭水龙头的时间,求出注入的水的体积,再根据长方体体积公式:体积=底面积×高;高=体积÷底面积,即可解答。
【详解】(1)根据分析可知,图中点B的位置表示停止注水。
(2)7时4分-7时=4分
6×4=24(立方分米)
24÷(4.8×2.5)
=24÷12
=2(分米)
答:玻璃缸中水的高度是2分米。
【点睛】本题考查了利用正比例图像及长方体体积公式解决问题,需熟练掌握正比例图像特点,灵活使用长方体体积公式。
8.1.6π平方厘米
【分析】根据体积的意义可知,把这块橡皮泥无论捏成什么形状,体积不变。根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】π×(4÷2)2×12÷10
π×4×12÷10
=16π÷10
=1.6π(平方厘米)
答:圆柱形的底面积是1.6π平方厘米。
【点睛】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
9.2260.8平方米
【分析】80厘米=0.8米,先根据圆柱的侧面积公式:S=πdh,用3.14×0.8×1.5即可求出滚动1周压过的面积,已知每分钟滚动10周,则用3.14×0.8×1.5×10×60即可求出一小时能压多少平方米的路面。
【详解】80厘米=0.8米
1小时=60分
3.14×0.8×1.5×10×60
=3.768×10×60
=2260.8(平方米)
答:一小时能压2260.8平方米的路面。
【点睛】本题考查了圆柱的侧面积公式的灵活应用。
10.450毫升
【分析】根据题意,先用体积360毫升除以高16厘米求出瓶子的底面积,瓶子的容积=饮料的体积+倒放时空余部分的体积,瓶子的容积也就是求高为(16+4)厘米的圆柱的容积;根据圆柱的体积(容积)公式:V=Sh,代入数据计算即可。
【详解】360÷16×(16+4)
=22.5×20
=450(毫升)
答:这个瓶子的容积是450毫升。
【点睛】解决此题的关键是理解前后两次瓶子的放置,后面空余部分的体积就是前面空余部分的体积。
11.(1)113.04平方米
(2)125.6吨
【分析】(1)由于蓄水池无盖,所以抹水泥部分是这个圆柱的侧面和一个底面,根据圆柱的侧面积=底面周长×高,圆的面积公式:S=πr2,把数据代入公式解答。
(2)根据圆柱的体积公式:V=πr2h,把数据代入公式求出水的体积,然后用水的体积乘每立方米水的质量即可。
【详解】(1)3.14×8×2.5+3.14×(8÷2)2
=25.12×2.5+3.14×16
=62.8+50.24
=113.04(平方米)
答:抹水泥部分的面积是113.04平方米。
(2)3.14×(8÷2)2×2.5×1
=3.14×16×2.5×1
=50.24×2.5×1
=125.6×1
=125.6(吨)
答:这个蓄水池能容纳125.6吨水。
【点睛】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是熟记公式。
12.5.25厘米
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,那么h=V÷÷πr2,把数据代入公式解答。
【详解】3.14×42×7÷÷(3.14×82)
=3.14×16×7÷÷(3.14×64)
=351.68×3÷200.96
=1055.04÷200.96
=5.25(厘米)
答:熔转成的圆锥体的高是5.25厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,关键是熟记公式。
13.126平方分米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆柱形水桶的底面半径;因为是无盖,再根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,求出一个水桶需要的铁皮,再乘2,即可解答。
【详解】12.56÷3.14÷2
=4÷2
=2(分米)
(3.14×22+3.14×2×2×4)×2
=(3.14×4+6.28×2×4)×2
=(12.56+12.56×4)×2
=(12.56+50.24)×2
=62.8×2
=125.6
≈126(平方分米)
答:至少需铁皮126平方分米。
【点睛】熟练掌握圆柱的表面积公式是解答本题的关键。
14.(1)abh;a3;Sh;(2)Sh;(3)450毫升
【分析】(1)根据长方体体积公式:长方体的体积=长×宽×高,正方体的体积公式:正方体的体积=棱长×棱长×棱长,圆柱的体积公式:圆柱的体积=底面积×高,据此解答;
(2)因为长方体的底面积=长×宽,正方体的底面积=棱长×棱长,据此可知,柱体的体积=底面积×高,据此解答;
(3)观察发现,底面是一个梯形,根据梯形的面积公式求出底面积,然后再乘高,即可求出牛奶的容积。
【详解】(1)V长方体=abh
V正方体=a3
V圆柱=Sh
(2)发现共同规律:V柱体=Sh
(3)(5+10)×6÷2
=15×6÷2
=45(平方厘米)
45×10=450(立方厘米)
450立方厘米=450毫升
答:这种牛奶盒的容积是450毫升。
【点睛】本题主要考查了圆柱的体积公式、长方体的体积公式、正方体的体积公式的灵活应用。
15.(1)529.92平方分米;(2)803.84升
【分析】(1)观察题意可知,长方形的宽是2个底面直径,长方形的长是一个底面直径和一个底面周长的和,已知底面直径为8分米,根据底面周长公式:C=πd,用2×8即可求出长方形的宽,用8+3.14×8即可求出长方形的长,然后根据长方形的面积公式,求出原来的长方形铁皮面积;
(2)观察题意可知圆柱的底面直径是8分米,高是(8×2)分米,根据圆柱的体积公式,代入数据解答即可。
【详解】(1)2×8=16(分米)
8+3.14×8
=8+25.12
=33.12(分米)
16×33.12=529.92(平方分米)
答:原来的长方形铁皮面积是529.92平方分米。
(2)3.14×(8÷2)2×8×2
=3.14×42×8×2
=3.14×16×8×2
=803.84(立方分米)
803.84立方分米=803.84升
答:做成的这个圆柱形油桶的容积是803.84升。
【点睛】本题考查了长方形和圆柱展开图之间的关系、长方形面积公式和圆柱体积公式的灵活应用。
16.(1)①④或②③
(2)选择①④:28.26千克
选择②③:37.68千克
【分析】(1)根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开后是一个长方形,这个长方形的长等于圆柱的底面周长,这个长方形的宽等于圆柱的高。由此可知,有两种不同的选择,可以选①和④,也可以选②和③,据此解答。
(2)根据圆柱的容积(体积)公式:,把数据代入公式求出这个圆柱形水桶的容积,然后再乘每升水的质量即可。
【详解】(1)①④或②③
(2))选择①④:
=3.14××4
=3.14×2.25×4
=7.065×4
=28.26(立方分米)
28.26立方分米=28.26升=28.26千克
答:最多能装水28.26千克。
选择②③:
=3.14××3
=3.14×4×3
=12.56×3
=37.68(立方分米)
37.68立方分米=37.68升=37.68千克
答:最多能装水37.68千克。
【点睛】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆柱的容积(体积)公式及应用,关键是熟记公式。
17.1厘米
【分析】水面上升的体积=圆锥体积,根据圆锥体积=底面积×高÷3,求出圆锥形钢锭体积,钢锭体积÷圆柱形容器底面积=水面上升的高度,据此列式解答。
【详解】3.14××12÷3÷[3.14×]
=3.14×52×12÷3÷[3.14×102]
=3.14×25×12÷3÷[3.14×100]
=314÷314
=1(厘米)
答:容器中的水面会上升1厘米。
【点睛】关键是掌握并灵活运用圆柱和圆锥的体积公式。
18.0.75米
【分析】水面下降的体积就是圆锥体积,水槽长×宽×水面下降的高度=圆锥体积,根据圆锥的高=体积×3÷底面积,列式解答即可。
【详解】5分米=0.5米、6.28厘米=0.0628米、40厘米=0.4米
1×0.5×0.0628=0.0314(立方米)
0.0314×3÷[3.14×(0.4÷2)2]
=0.0942÷[3.14×0.22]
=0.0942÷[3.14×0.04]
=0.0942÷0.1256
=0.75(米)
答:这个圆锥形零件的高是0.75米。
【点睛】关键是掌握并灵活运用长方体和圆锥体积公式,利用转化思想,先求出圆锥体积。
19.150.72立方米
【分析】该图形的容积等于下方圆柱的容积加上上方圆锥的容积,根据圆柱的容积公式:V=πr2h,圆锥的容积公式:V=πr2h,据此代入数值进行计算即可。
【详解】3.14×(4÷2)2×10+×3.14×(4÷2)2×(16-10)
=3.14×4×10+×3.14×4×6
=125.6+25.12
=150.72(立方米)
答:该整流罩的容积是150.72立方米。
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
20.3200平方米
【分析】根据实际距离=图上距离÷比例尺,据此求出这块草坪的底和高的实际长度,再根据三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】2.5÷=20000(厘米)=200(米)
0.4÷=3200(厘米)=32(米)
200×32÷2
=6400÷2
=3200(平方米)
答:这块三角形草地的实际面积是3200平方米。
【点睛】本题考查比例尺,结合三角形的面积的计算方法是解题的关键。
21.87.92平方分米
【分析】“”求需要铁皮的面积就是求圆柱的表面积,因为这个圆柱形水桶无盖,所以只计算圆柱的侧面积和一个底面积,据此解答。
【详解】2×3.14×2×6+3.14×22
=6.28×2×6+12.56
=12.56×6+12.56
=75.36+12.56
=87.92(平方分米)
答:做这个水桶至少要用87.92平方分米铁皮。
【点睛】本题主要考查圆柱表面积公式的应用,明确需要去掉一个圆柱的底面积是解答题目的关键。
22.(1)28.26平方米;
(2)24.021吨
【分析】(1)求这个沙堆的占地面积,实际上是求圆锥的底面积,根据圆的面积公式S=代入数据即可得解。
(2)利用圆锥的体积公式:V=,代入数据求出圆锥形沙堆的体积,再乘每立方米沙堆的重量,即可求出这堆沙大概的重量。
【详解】(1)3.14×(6÷2)2
=3.14×32
=3.14×9
=28.26(平方米)
答:这个沙堆的占地面积是28.26平方米。
(2)28.26×1.5×1.7
=9.42×1.5×1.7
=14.13×1.7
=24.021(吨)
答:这堆沙约重24.021吨。
【点睛】此题的解题关键是灵活运用圆锥的底面积以及圆锥的体积公式求解。
23.10吨
【分析】首先根据底面周长是12.56m,求出圆锥的底面半径,再根据圆锥的体积公式:V=sh,求出沙堆的体积,然后用沙的体积乘每立方米沙的质量即可。
【详解】12.56÷3.14÷2
=4÷2
=2(米)
×3.14×22×1.5
=×(3.14×4×1.5)
=×(12.56×1.5)
=×18.84
=6.28(立方米)
6.28×1.6≈10(吨)
答:这堆沙子约重10吨。
【点睛】此题主要考查圆锥的体积公式在实际生活中的应用,掌握圆锥的体积计算公式是解答本题的关键。
24.1884立方厘米
【分析】根据圆柱的体积公式:V=πr2h,圆锥的体积公式:V=πr2h,用3.14×(10÷2)2×20即可求出圆柱的体积,用3.14×(10÷2)2×12×即可求出圆锥的体积,最后把两部分相加即可。
【详解】3.14×(10÷2)2×20
=3.14×52×20
=3.14×25×20
=1570(立方厘米)
3.14×(10÷2)2×12×
=3.14×52×12×
=3.14×25×12×
=314(立方厘米)
1570+314=1884(立方厘米)
答:火箭模型1884立方厘米。
【点睛】本题主要考查了圆柱体积公式和圆锥体积公式的应用。
25.30.6厘米
【分析】将圆锥浸没在水中后,水面上升部分的体积和圆锥的体积相等。圆锥体积=底面积×高÷3,圆柱体积=底面积×高。据此,先求出圆锥的体积,再将圆锥的体积除以圆柱的底面积,求出水面上升了多少,最后利用加法求出这时玻璃容器中的水高。
【详解】20÷2=10(厘米)
3.14×32×20÷3÷(3.14×102)
=188.4÷314
=0.6(厘米)
30+0.6=30.6(厘米)
答:这时玻璃容器中的水高30.6厘米。
【点睛】本题考查了圆柱和圆锥的体积,灵活运用圆柱和圆锥的体积公式是解题的关键。
26.(1)3
(2)见详解
【分析】(1)根据题干描述,古代的圆柱体积计算方法为:V=C2×h÷12,现在方法是V=Sh,通过化简即可得出圆周率的取值;
(2)现在的方法:圆柱的体积公式V=Sh,先算出底面圆的半径,再把数据代入公式,即可得出答案。
古人的方法:根据题干描述,古代的圆柱体积计算方法为:V=C2×h÷12,将数据代入公式,即可得出答案。
【详解】(1)C2×h÷12=Sh
(2r)2×h÷12=r2×h
=3
圆周率的取值是3。
(2)方法1:(18÷3÷2)2×3×10
=9×3×10
=270(立方厘米)
方法2:18×18×10÷12
=3240÷12
=270(立方厘米)
答:圆柱的体积是270立方厘米。
【点睛】本题考查学生对现代和古人求圆柱体积方法的掌握和运用,本题要注意π的取值为3。
27.12π平方分米;0.5π分米。
【分析】因为水与圆柱体的容器的接触面只有侧面和底面,根据圆柱的表面积公式S=侧面积+底面积,将数据代入即可得出答案。
把圆柱体中的水倒入正方体容器内,水的体积不变,根据圆柱的体积公式V=Sh,先求出水的体积,再根据h=V÷S(正方形面积公式S=棱长×棱长),将数据代入,即可得出水面高度
【详解】4π×2+(4÷2)2×π
=8π+22×π
=8π+4π
=12π(平方分米)
(4÷2)2×π×2÷(4×4)
=22×π×2÷16
=8π÷16
=0.5π(分米)
答:水与圆柱体的接触面积是12平方分米,水面高0.5π分米。
【点睛】本题考查学生对圆柱表面公式和圆柱体积公式的掌握和运用,解答时要注意水从圆柱体中倒入正方体容器内,水的体积不变。
28.(1)6000平方米
(2)50.24平方米
【分析】(1)先求出一个大棚的占地面积,利用长方形的面积S=长×宽即可求出一个大棚的占地面积,再乘大棚的数量;
(2)求搭建一个大棚大约要用多少平方米的塑料薄膜就是求半个圆柱的侧面积和一个底面积的和,利用公式S=πr2+πdh÷2即可。
【详解】(1)2×15×200
=30×200
=6000(平方米)
答:这些大棚的种植面积共有6000平方米。
(2)3.14×(2÷2)2+3.14×2×15÷2
=3.14×1+6.28×15÷2
=3.14+94.2÷2
=3.14+47.1
=50.24(平方米)
答:搭建一个大棚大约要用50.24平方米的塑料薄膜。
【点睛】本题考查了圆柱的侧面积计算公式的应用。
29.6π平方厘米
【分析】先根据圆柱的体积公式(V=πr2h)先算出圆柱形橡皮泥的体积,再根据橡皮泥体积不变,利用长方体体积公式(V=abh)即可求出长方体的底面积是多少平方厘米。
【详解】(4÷2)2×15×π
=4×15×π
=60π(立方厘米)
60π÷10=6π(平方厘米)
答:这个长方体的底面积是6π平方厘米。
【点睛】此题主要考查长方体和圆柱体的体积计算方法,关键是明白橡皮泥的体积不变。
30.32厘米
【分析】根据题意可知把圆锥形的沙堆填在长方体沙坑里,沙的体积不变,根据圆锥的体积公式:VSh,求出沙的体积,然后用沙的体积除以长方体沙坑的底面积即可,据此解答。
【详解】36×0.8÷(7.5×4)
=12×0.8÷30
=9.6÷30
=0.32(米)
=32(厘米)
答:沙坑里沙子的厚度是32厘米。
【点睛】此题主要考查圆锥的体积公式、长方体的体积公式的灵活运用。
31.2.5吨
【分析】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形稻谷的体积,再用圆锥稻谷的体积×0.5,即可解答。
【详解】3.14×(4÷2)2×1.2××0.5
=3.14×4×1.2××0.5
=12.56×1.2××0.5
=15.072××0.5
=5.024×0.5
=2.512
≈2.5(吨)
答:这个稻谷堆大约2.5吨。
【点睛】熟练掌握圆锥的体积公式是解答本题的关键。
32.75.36平方分米
【分析】根据题意,水桶外围一圈的长度就是这个圆柱形水桶的底面周长,根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出底面半径;求这个水桶至少要木板多少平方分米,就是求这个水桶的表面积,根据圆柱的表面积公式:表面积=底面积+侧面积,代入数据,即可解答。
【详解】3.14×(12.56÷3.14÷2)2+12.56×5
=3.14×(4÷2)2+62.8
=3.14×4+62.8
=12.56+62.8
=75.36(平方分米)
答:做这个水桶至少要木板75.36平方分米。
【点睛】本题考查圆柱的表面积公式的应用,注意这个无盖圆柱形水桶的表面积是一个底面积与侧面积的和。
33.4710平方分米
【分析】压路机的前轮滚动一周压过的面积就是圆柱形前轮的侧面积,根据侧面积=πdh求出侧面积,再乘上10就是前轮转动10周压过的面积,据此解答即可。
【详解】1.5米=15分米
3.14×10×15×10
=31.4×15×10
=471×10
=4710(平方分米)
答:压过的面积是4710平方分米。
【点睛】此题主要考查圆柱侧面积公式的灵活运用,关键是熟记公式。
34.(1)6.28立方米;
(2)4082千克;
(3)10205千克;
(4)11429.6元
【分析】(1)根据圆锥的体积公式:V=πr2h,据此计算出这堆稻谷的体积;
(2)用稻谷的体积乘每立方米稻谷的重量即可求解;
(3)用稻谷的重量除以稻谷的面积即可;
(4)根据单价×数量=总价,用稻谷的重量乘2.8即可求解。
【详解】(1)×3.14×(4÷2)2×1.5
=×3.14×4×1.5
=×3.14×(4×1.5)
=×3.14×6
=×6×3.14
=2×3.14
=6.28(立方米)
答:这堆稻谷的体积是6.28立方米。
(2)6.28×650=4082(千克)
答:这堆稻谷重4082千克。
(3)4082÷0.4=10205(千克)
答:平均每公顷产稻谷10205千克。
(4)4082×2.8=11429.6(元)
答:这些稻谷能卖11429.6元。
【点睛】本题考查圆锥的体积,熟记公式是解题的关键。
35.(1)12.56立方米
(2)够用
【分析】(1)已知圆锥形沙堆的底面周长,根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆锥形沙堆的底面半径;然后根据圆锥的体积公式V=πr2h,代入数据计算,即可求出这些沙子的体积。
(2)根据长方体的体积公式V=abh,求出长方体沙坑需要沙子的体积,再与上一题的沙子体积比较,得出结论。注意单位的换算:1米=100厘米。
【详解】(1)圆锥的底面半径:
12.56÷3.14÷2
=4÷2
=2(米)
圆锥的体积:
×3.14×22×3
=×3.14×4×3
=12.56(立方米)
答:这些沙子的体积是12.56立方米。
(2)20厘米=0.2米
10×6.28×0.2
=62.8×0.2
=12.56(立方米)
答:这些沙子够用。
【点睛】本题考查圆锥底面周长、圆锥体积、长方体体积公式的灵活应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
