人教版小学数学三年级下册第八单元《数学广场——搭配(二)》专项训练——应用题(含答案)
文档属性
| 名称 | 人教版小学数学三年级下册第八单元《数学广场——搭配(二)》专项训练——应用题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 06:26:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版小学数学三年级下册
第八单元《数学广场——搭配二》专项训练——应用题
1.小明有10元和5元面值的人民币各5张,如果买一个50元的书包,有几种恰好付50元的方式?你喜欢哪种,说明原因。(用列表的方法解答)
2.一列“复兴号”高铁在苏州与南京之间往返行驶,中途经停无锡、常州两站,高铁站共需准备多少种不同车票?
3.书架上有3本不同的数学书,5本不同的语文书,6本不同的英语书。
(1)若从这些书中任取一本,有多少种不同的取法?
(2)若从这书中取数学书、语文书、英语书各一本,有多少种不同的取法?
(3)若是从这些书中取不同科目的两本,有多少种不同的取法?
4.小刚有5元和2元面值的人民币无数张,如果要买一个16元的钢笔,他可以怎样付钱?有几种情况?
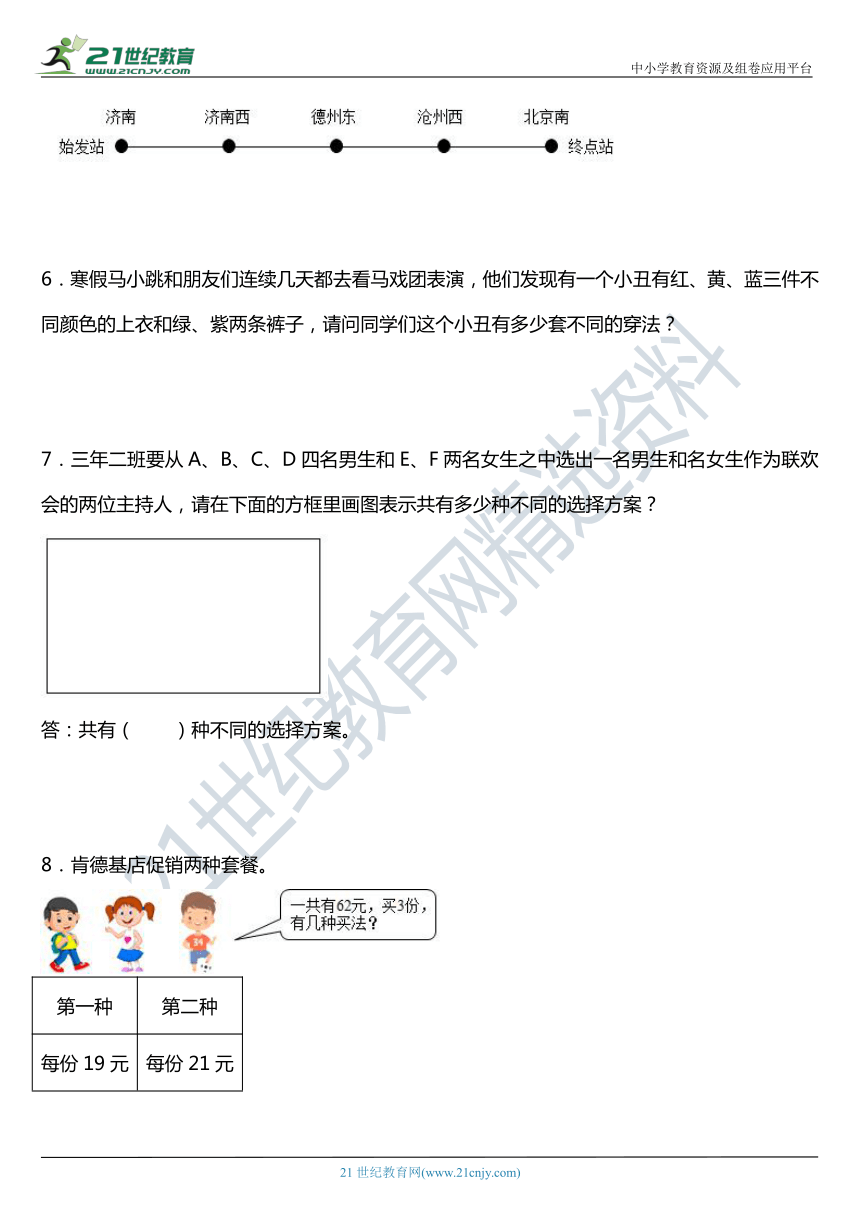
5.高铁G334次列车,在济南到北京的铁路沿线上共有5站(如下图)。请问铁路部门要为这趟列车准备多少种单程车票?
6.寒假马小跳和朋友们连续几天都去看马戏团表演,他们发现有一个小丑有红、黄、蓝三件不同颜色的上衣和绿、紫两条裤子,请问同学们这个小丑有多少套不同的穿法?
7.三年二班要从A、B、C、D四名男生和E、F两名女生之中选出一名男生和名女生作为联欢会的两位主持人,请在下面的方框里画图表示共有多少种不同的选择方案?
答:共有( )种不同的选择方案。
8.肯德基店促销两种套餐。
第一种 第二种
每份19元 每份21元
9.在《一千零一夜》里《阿里巴巴和四十大盗》的故事中,阿里巴巴最后战胜了大盗们,拥有了宝藏山洞,山洞打开的暗语之前是“芝麻开门”,现在同学们依然用这四个字,帮阿里巴巴编出其它不同的暗语,试着把它们全部写出来。
10.小军想买一份荤菜和一份素菜。
(1)根据上面的菜单,他有几种不同的选菜方法?
(2)总价不超过15元的有多少种选法?
(3)最便宜的搭配要花多少元?
11.下面有四本书,小明想从中任选两本书,共有( )种选法。(画出分析示意图)
12.17支排球队分成三组,其中两组各6支队,第三组5支队,第一阶段各组进行单循环比赛;第二阶段,由各组前两名举行单循环比赛,决出冠亚军,共需举行多少场比赛?若第二阶段中,原同一组的两队免赛,共需举行多少场比赛?若17支球队不分组,直接利用单循环赛制,共要赛多少场?
13.六一儿童节这天,王老师打算从下面4名同学中任选2名同学表演节目,有几种不同的选法?(画图表示,并回答问题)
14.小明一家要照一张全家福。要求爸爸、妈妈站中间位置,小明、妹妹站两边位置,一共有多少种不同的站法?(用自己喜欢的方法记录你的想法)
15.用0、2、6、8能组成多少个没有重复数字的小数?写出来?
(1)小于1而小数部分是三位小数。
(2)大于8而小数部分是三位小数。
16.小、莫、萱三人玩传球游戏,每次持球的人都可以把球传给另外两个人中的任何一个,先由小拿球,经过4次传球之后,球又回到了小的手里,那么一共有多少种不同的传球过程?
17.乌龟、兔子、米老鼠站成一排,如果乌龟不站在第1个,兔子不站在第2个,米老鼠不站在第3个,那么,它们共有多少种不同的站法?
18.如下图,如果小高站在1号地毯上,他想要走到5号地毯上,每次只能走到相邻的编号(两个六边形如果有公共边就成为相邻),而且只能向右边走(例如1→2→3→5就是一种可能的走法) ,那么小高一共有多少种不同的走法?
19.在寻宝游戏中小温通过努力,终于获得了一只宝箱。这只宝箱的密码是一个用2、5、7组成的没有重复数字的两位数。
(1)密码可能是哪个数?请把它们全部写出来,并把这些数按照从小到大的顺序排列。
(2)如果这组两位数按照以上的排列顺序不断重复出现,第145个数就是这只宝箱的密码,这个密码是什么数?(请写出你的思考过程。)
20.早餐时,粥和主食各取一种,共有( )种不同的搭配方法?连一连。
21.三年级4个班要在周五下午进行体育活动,项目是花样跳绳和足球。
(1)花样跳绳比赛14:20开始,每场比赛20分钟,准备10分钟。请你把表格里的比赛时间补充完整。
场次及班级 时间 地点
第一场:三1班 14:20—14:40 学校操场
第二场:三2班 ( )—15:10
第三场:三3班 ( )—( )
第四场:三4班 15:50—( )
(2)足球比赛项目,每两个班都要踢一场,一共踢( )场,请你在下面用画图的方式表示出踢的次数。
22.文具店里有3种不同的书包,4种不同的文具盒,妈妈要给小明买一个书包和一个文具盒,有多少种不同的买法?
23.刺绣是针线在织物上绣制各种装饰图案的总称,在中国至少有三千年的历史,主要有苏绣、湘绣、蜀绣和粤绣四大门类。下面是一家刺绣店的几款刺绣。
(1)如果买两个不同的绣屏,有几种不同的买法?
(2)如果买一个荷花绣屏和一个锦鲤绣屏,一共要付多少元?
24.小雪准备购买早餐,早餐饮品和主食织能各逃择一种。
(1)共有多少种早餐搭配方案?
(2)小雪只带了5元钱,她买了一称牛奶,剩下的钱够买一根油条吗?
25.小甲和小乙两人进行围棋赛,谁先胜三局就赢得比赛,如果最后小甲获胜了,那么比赛的过程有多少种可能?
参考答案:
1.见详解
【分析】先全部付10元的人民币得5张,然后10元人民币张数逐渐减少,5元人民币张数增加,注意10元减少1张,5元得增加2张,但5元人民币不得超过5张,据此列表即可解答
【详解】
方案 10元 5元 总钱数
① 5张 0张 50元
② 4张 2张 50元
③ 3张 4张 50元
一共有3种方式,我喜欢付5张10元,这样简单。
【点睛】不管哪种方式,付出10元和5元面值的人民币钱数和等于50元,这是解答本题的关键。
2.12种
【分析】仔细读题,已知条件“一列高铁在苏州与南京之间往返行驶”,说明苏州和南京分别是起点与终点,加上中间停靠2站,此路线共有4站,如下左图可得出答案。
【详解】由题意及分析得:要准备车票3+2+1=6(种)。还要考虑“往返”,准备的车票应是6×2=12(种)。
答:高铁站共需准备12种不同车票。
【点睛】本题主要考查的是搭配问题,解题的关键是熟练运用每种搭配,确保不遗漏每一次搭配,进而得出答案。
3.(1)14种;
(2)90种;
(3)63种
【分析】(1)若从这些书中任取一本,可以有3类办法:第一类办法是从3本不同的数学书任取一本,有3种取法;同理,从5本不同的语文书取一本有5种取法;从6本不同的英语书取一本有6种取法,这样一共有3+5+6=14(种);
(2)若从这书中取数学书、语文书、英语书各一本,需要分成三个步骤完成,第一步取1本数学书,有3种取法;第二步取1本语文书,有5种取法;第三步取1本英语书,有6种取法,根据乘法原理共有:3×5×6=90(种)取法;
(3)若是从这些书中取不同科目的两本,可以有3类办法:第一类办法是数学书、语文书各取一本,需要两个步骤,有3×5=15种方法;第二类办法取数学书和英语书各取一本,需要两个步骤,有3×6=18种方法;第三类办法取语文书和英语书各取一本,需要两个步骤,有5×6=30种方法;一共有30+15+18=63(种)。
【详解】由分析得,
(1)3+5+6
=8+6
=14(种)
答:若从这些书中任取一本,有14种不同的取法。
(2)3×5×6
=15×6
=90(种)
答:若从这书中取数学书、语文书、英语书各一本,有90种不同的取法
(3)语英:5×6=30(种)
语数:5×3=15(种)
英数:3×6=18(种)
总:30+15+18
=45+18
=63(种)
答:若是从这些书中取不同科目的两本,有63种不同的取法。
【点睛】此题考查的是排列组合,解答此题关键是为了做到不遗漏不重复,按一定顺序排列组合。
4.5元2张,2元3张或者2元8张;有两种情况。
【分析】纸币只有5元和2元,16元里有几个5元和几个2元的组合,分贝列举出来即可。
【详解】情况一:5元2张,2元3张;
5×2+2×3
=10+6
=16(元)
情况二:2元8张;
2×8=16(元)
答:可以付2张5元,3张2元;或8张2元的;有2种情况。
【点睛】解答此题的关键是分别列举出情况。
5.10种
【分析】从济南出发有4种单程票;
从济南西出发有3种单程票;
从德州东出发有2种单程票;
从沧州西出发1种单程票;
因此将这些单程票的种类加起来即可。
【详解】4+3+2+1=10(种)
答:铁路部门要为这趟列车准备10种单程车票。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
6.6套
【分析】根据题意,用画图连线的形式表示出裤子和上衣,连线表示一种穿法,数出连线数即可。
【详解】搭配方式如图:
由图可知总共有6套不同的穿法。
答:小丑有6套不同的穿法。
【点睛】本题为典型的搭配问题,用图示方法个人能够容易理解搭配问题的解法。
7.图见详解过程;8
【分析】根据题意,A与E、F有2种方案,B与E、F有2种方案,C与E、F有2种方案,D与E、F有2种方案,一共有4×2=8种选择方案,据此解答即可。
【详解】如图所示:
4×2=8(种)
答:共有8种不同的选择方案。
【点睛】乘法原理:即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法……,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×……×Mn种不同的方法。
8.三种
【分析】已知总共只有62元,需要买3份,则需要满足三份的价钱不超过62元即可,以此列出有几种可能。
【详解】19×3=57<62,所以第一种最多买3份
21×3=63>62,所以第二种最多买2份
综合上述可得到以下几种方案:①第一种3份;②第一种2份、第二种1份;③第一种1份、第2种两份。所以62元买3份有三种买法。
答:62元买3份有三种买法。
【点睛】本题考查数量运算解决实际问题,明确两种不同套餐最多/少买几份是解答此题的关键。
9.见详解
【分析】当第1个字是芝时,还可以组成芝麻门开、芝开麻门、芝开门麻、芝门麻开、芝门开麻;同理可以写出第1个字是麻、开或门的组成暗语,据此即可解答。
【详解】根据分析可得:
芝麻门开、芝开麻门、芝开门麻、芝门麻开、芝门开麻;
麻芝开门、麻芝门开、麻开芝门、麻开门芝、麻门芝开、麻门开芝;
开芝麻门、开芝门麻、开麻芝门、开麻门芝、开门麻芝、开门芝麻;
门芝麻开、门芝开麻、门麻芝开、门麻开芝、门开芝麻、门开麻芝。
【点睛】本题主要考查学生对搭配知识的掌握和灵活运用。
10.(1)9种
(2)6种
(3)11.4元
【分析】(1)小军要选一份荤菜和一份,菜单中荤菜共3种,青菜也是3种,共有3×3=9(种)不同的选菜方法;
(2)将每一种搭配按照价钱算出来与15元进行比较即可知道总价不超过15元的有多少种选法;
(3)根据第二问直接得到最便宜的搭配方法。
【详解】(1)3×3=9(种)
答:他有9种不同的选菜方法。
(2)熏干芹菜+宫保鸡丁=3.8+8.8=12.6(元)<15元;
熏干芹菜+炸肉串=3.8+9.5=13.3(元)<15元;
熏干芹菜+炖排骨=3.8+12.6=16.4(元);
炒胡萝卜+宫保鸡丁=3.2+8.8=12(元)<15元;
炒胡萝卜+炸肉串=3.2+9.5=12.7(元)<15元;
炒胡萝卜+炖排骨=3.2+12.6=15.8(元);
烧茄子+宫保鸡丁=2.6+8.8=11.4(元)<15元;
烧茄子+炸肉串=2.6+9.5=12.1(元)<15元;
烧茄子+炖排骨=2.6+12.6=15.2(元);
答:总价不超过15元的有6种选法。
(3)最便宜的为烧茄子+宫保鸡丁=2.6+8.8=11.4(元)
答:最便宜的搭配要花11.4元。
【点睛】本题考查的是简单的搭配问题,关键是注意搞清楚搭配,做到不重不漏。
11.6;画图见详解
【分析】根据搭配的方法进行两两连线,应依次连线,避免遗漏,但是又不能重复。
【详解】
如图所示,小明想从中任选两本书,一共有6种不同的选法。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
12.55场;52场;136场
【分析】单循环赛制的场数=队伍数×(队伍数-1)÷2,根据这个公式分别计算;注意第二种情况下,三组各有两队不需要再比赛,因此要减少3场比赛。
【详解】6×(6-1)÷2×2+5×(5-1)÷2
=6×5÷2×2+5×4÷2
=30+10
=40(场)
40+6×(6-1)÷2
=40+6×5÷2
=40+15
=55(场)
55-3=52(场)
17×(17-1)÷2
=17×16÷2
=136(场)
答:第一种情况共需要55场;第二种情况共需要52场;第三种情况共需要136场。
【点睛】本题考查排列组合的知识,关键是掌握循环赛问题的求解方法。
13.6种
【分析】每个人都可以和其他的1个人一起表演节目,即两两组合,据此列举即可。
【详解】如图:
①和②、①和③、①和④、②和③、②和④、③和④;
所以共有6种不同的选法。
答:共有6种选法;①和②、①和③、①和④、②和③、②和④、③和④。
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人比较多可以用公式:握手次数解答。
14.4种
【分析】根据题意,4个人的位置按题目要求排列,列举出所有情况,得出结论。
【详解】4个人的不同站法如下:
①小明、爸爸、妈妈、妹妹;
②小明、妈妈、爸爸、妹妹;
③妹妹、爸爸、妈妈、小明;
④妹妹、妈妈、爸爸、小明;
答:一共有4种不同的站法。
【点睛】也可以用乘法原理解答,爸爸、妈妈站中间位置,有2种选择;小明、妹妹站两边位置,也有2种选择;一共有2×2=4种不同的站法。
15.(1)0.268、0.286、0.628、0.682、0.826、0.862
(2)8.062、8.026、8.620、8.602、8.260、8.206
【分析】(1)整数部分只能是0,剩下3个数字都在小数部分,列举即可。
(2)要求大于8,这四个数字中,最大的就是8,小数部分又是三位数的小数,所以整数部分是8,其余在小数部分,列举即可。
【详解】(1)小于1而小数部分是三位小数:0.268、0.286、0.628、0.682、0.826、0.862。
(2)大于8而小数部分是三位的小数:8.062、8.026、8.620、8.602、8.260、8.206。
【点睛】本题考查了排列组合知识的灵活应用,关键是确定整数部分。
16.6种
【分析】先考虑第1次有多少种传法?然后用树形图画出每次传球后给谁。要注意只有第4次传球后回到小手上的才是符合题意的传法。
【详解】由题意可知,小先拿球,则第1次可以给莫也可以给萱。
由题意画树形图如下:
由图可知,共有6种情况符合要求。
答:一共有6种不同的传球过程。
【点睛】根据题意分析出第1次只能给莫或萱,据此正确画出树形图是解题关键。
17.2种
【分析】可以先考虑第1个位置可以站哪些小动物?再考虑第2个位置。以第一个位置站的小动物为“树根”,画出树形图,即可得到所有的站法。
【详解】由题意,画树形图如下:
由图可知,有2种不同的站法。
答:它们共有2种不同的站法。
【点睛】树形图是枚举法的一种,可以使我们的枚举过程更加直观,有条理又不易重复或遗漏。
18.5种
【分析】根据题意,小高第一步可以走到2号地毯或3号地毯,据此注意分析即可,注意题目中的限定条件:相邻编号地毯和只能向右走,另外只有结束在5号地毯的才符合题意。
【详解】根据题意,画图如下:
数一数可知,一共5种可能。
答:小高一共有5种不同的走法。
【点睛】解答此类问题,按照树形图的画法逐一画出所有的分叉即可。注意不重复不遗漏。
19.(1)密码可能是:25、27、52、57、72、75,从小到大排列为:25<27<52<57<72<75;
(2)25,根据题意可知,这组两位数按照以上的排列顺序不断重复出现,每六个数是一组,145除以6,总共出现了24组,余下一个数,即这个数的密码就是第一个数为25
【分析】(1)先将组成的两位数依次写出来,分别由25、52、57、75、27、72,然后按照数的大小依次排列即可;(2)根据题意可知,这组两位数按照以上的排列顺序不断重复的,每六个数是一组,用145除以6,会发现共有24组,余下一个数就是第145个数为25,据此解答。
【详解】(1)密码可能是哪个数?请把它们全部写出来,并把这些数按照从小到大的顺序排列。
答:组成没有重复的两位数:25、27、52、57、72、75;从小到大的顺序排列为:25<27<52<57<72<75。
(2)如果这组两位数按照以上的排列顺序不断重复出现,第145个数就是这只宝箱的密码,这个密码是什么数?(请写出你的思考过程。)
根据题意可知,这组两位数按照以上的排列顺序不断重复出现,每六个数是一组,145除以6,总共出现了24组,余下一个数,即这个数的密码就是第一个数为25。
【点睛】熟练掌握根据给出的数字组成没有重复的数字的方法是解答本题的关键。
20.9;见详解
【分析】每种主食都可以和每种粥搭配在一起,则小米粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。绿豆粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。蔬菜粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。则一共能3+3+3=9种不同的搭配方法。
【详解】早餐时,粥和主食各取一种,共有9种不同的搭配方法。
【点睛】本题考查搭配问题,采用枚举法解答。
21.(1)14:50;15:20;15:40;16:10;
(2)6;图见详解
【分析】(1)经过的时间等于结束的时间减去开始的时间即可;
(2)根据题意,每两个班都要踢一次,画出一个长方形,再画出它的对角线,四个角标出1~4,就是所踢的次数,据此解答。
【详解】(1)花样跳绳比赛14:20开始,每场比赛20分钟,准备10分钟。请你把表格里的比赛时间补充完整。
场次及班级 时间 地点
第一场:三1班 14:20—14:40 学校操场
第二场:三2班 (14:50)—15:10
第三场:三3班 (15:20)—(15:40)
第四场:三4班 15:50—(16:10)
(2)足球比赛项目,每两个班都要踢一场,一共踢(6)场,请你在下面用画图的方式表示出踢的次数。
【点睛】本题主要考查时间和日期以及握手问题,熟练掌握并灵活运用。
22.12种
【分析】妈妈要给小明买一个书包和一个文具盒,从3种不同的书包中选1种,有3种选法;从4种不同的文具盒中选1种,有4种选法;根据乘法原理共有3×4=12(种)不同的买法。
【详解】根据分析得:
3×4=12(种)
答:有12种不同的买法。
【点睛】做这类搭配类题目时,我们要做到有序、不重复、不遗漏。所以一定要按照一定顺序来思考问题才能考虑周全。
23.(1)6种;(2)93.2元
【分析】(1)如果买两个不同的绣屏,就相当于4选2,根据握手问题的计算方法:握手次数=人数×(人数-1)÷2,代入数据计算即可。
(2)求买一个荷花绣屏和一个锦鲤绣屏,一共要付多少元,把两种物品的单价相加即可。
【详解】(1)4×(4-1)÷2
=4×3÷2
=12÷2
=6(种)
答:如果买两个不同的绣屏,有6种不同的买法。
(2)23.7+69.5=93.2(元)
答:如果买一个荷花绣屏和一个锦鲤绣屏,一共要付93.2元。
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式:握手次数=人数×(人数-1)÷2解答解答。
24.(1)6种;(2)够
【分析】(1)用饮料的种类乘主食的种类,可以计算出共有多少种早餐搭配方案。
(2)用小雪带的钱数减去牛奶的钱数,可以计算出剩余的钱数,再用剩余的钱数与油条的钱数比较即可。
【详解】(1)2×3=6(种)
答:共有6种早餐搭配方案。
(2)5-2.8=2.2(元)
2.2>2
答:剩下的钱够买一根油条。
【点睛】本题解题关键是熟练掌握搭配原理的计算方法,再根据小数减法的意义列式计算。
25.10种
【分析】试着把每场比赛的结果用树形图表示出来。注意:不会有“小乙-小甲-小乙-小乙-小甲”这样的过程出现,因为这种情况下,塞完第4场后小乙已经获胜,不合题意。
【详解】第一场小甲胜时:
第一场小乙胜时:
综上,共有10种可能。
答:比赛的过程有10种可能。
【点睛】树形图是枚举法的一种,可以使我们的枚举过程更加直观,有条理又不易重复或遗漏。
26.2种
【分析】首先根据题意,甲、丁都不站在第1个,所以第1个只能是乙或者丙,以此为“树根”,画树形图解答即可。
【详解】由题意可知:第1个只能是乙或者丙。
第1个是乙时:
第1个是丙时:
综上,一共有2种。
答:一共有2种不同的站队方法。
【点睛】树形图是枚举法的一种,画树状图的关键一是确定层数,二是确定每层分叉的个数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版小学数学三年级下册
第八单元《数学广场——搭配二》专项训练——应用题
1.小明有10元和5元面值的人民币各5张,如果买一个50元的书包,有几种恰好付50元的方式?你喜欢哪种,说明原因。(用列表的方法解答)
2.一列“复兴号”高铁在苏州与南京之间往返行驶,中途经停无锡、常州两站,高铁站共需准备多少种不同车票?
3.书架上有3本不同的数学书,5本不同的语文书,6本不同的英语书。
(1)若从这些书中任取一本,有多少种不同的取法?
(2)若从这书中取数学书、语文书、英语书各一本,有多少种不同的取法?
(3)若是从这些书中取不同科目的两本,有多少种不同的取法?
4.小刚有5元和2元面值的人民币无数张,如果要买一个16元的钢笔,他可以怎样付钱?有几种情况?
5.高铁G334次列车,在济南到北京的铁路沿线上共有5站(如下图)。请问铁路部门要为这趟列车准备多少种单程车票?
6.寒假马小跳和朋友们连续几天都去看马戏团表演,他们发现有一个小丑有红、黄、蓝三件不同颜色的上衣和绿、紫两条裤子,请问同学们这个小丑有多少套不同的穿法?
7.三年二班要从A、B、C、D四名男生和E、F两名女生之中选出一名男生和名女生作为联欢会的两位主持人,请在下面的方框里画图表示共有多少种不同的选择方案?
答:共有( )种不同的选择方案。
8.肯德基店促销两种套餐。
第一种 第二种
每份19元 每份21元
9.在《一千零一夜》里《阿里巴巴和四十大盗》的故事中,阿里巴巴最后战胜了大盗们,拥有了宝藏山洞,山洞打开的暗语之前是“芝麻开门”,现在同学们依然用这四个字,帮阿里巴巴编出其它不同的暗语,试着把它们全部写出来。
10.小军想买一份荤菜和一份素菜。
(1)根据上面的菜单,他有几种不同的选菜方法?
(2)总价不超过15元的有多少种选法?
(3)最便宜的搭配要花多少元?
11.下面有四本书,小明想从中任选两本书,共有( )种选法。(画出分析示意图)
12.17支排球队分成三组,其中两组各6支队,第三组5支队,第一阶段各组进行单循环比赛;第二阶段,由各组前两名举行单循环比赛,决出冠亚军,共需举行多少场比赛?若第二阶段中,原同一组的两队免赛,共需举行多少场比赛?若17支球队不分组,直接利用单循环赛制,共要赛多少场?
13.六一儿童节这天,王老师打算从下面4名同学中任选2名同学表演节目,有几种不同的选法?(画图表示,并回答问题)
14.小明一家要照一张全家福。要求爸爸、妈妈站中间位置,小明、妹妹站两边位置,一共有多少种不同的站法?(用自己喜欢的方法记录你的想法)
15.用0、2、6、8能组成多少个没有重复数字的小数?写出来?
(1)小于1而小数部分是三位小数。
(2)大于8而小数部分是三位小数。
16.小、莫、萱三人玩传球游戏,每次持球的人都可以把球传给另外两个人中的任何一个,先由小拿球,经过4次传球之后,球又回到了小的手里,那么一共有多少种不同的传球过程?
17.乌龟、兔子、米老鼠站成一排,如果乌龟不站在第1个,兔子不站在第2个,米老鼠不站在第3个,那么,它们共有多少种不同的站法?
18.如下图,如果小高站在1号地毯上,他想要走到5号地毯上,每次只能走到相邻的编号(两个六边形如果有公共边就成为相邻),而且只能向右边走(例如1→2→3→5就是一种可能的走法) ,那么小高一共有多少种不同的走法?
19.在寻宝游戏中小温通过努力,终于获得了一只宝箱。这只宝箱的密码是一个用2、5、7组成的没有重复数字的两位数。
(1)密码可能是哪个数?请把它们全部写出来,并把这些数按照从小到大的顺序排列。
(2)如果这组两位数按照以上的排列顺序不断重复出现,第145个数就是这只宝箱的密码,这个密码是什么数?(请写出你的思考过程。)
20.早餐时,粥和主食各取一种,共有( )种不同的搭配方法?连一连。
21.三年级4个班要在周五下午进行体育活动,项目是花样跳绳和足球。
(1)花样跳绳比赛14:20开始,每场比赛20分钟,准备10分钟。请你把表格里的比赛时间补充完整。
场次及班级 时间 地点
第一场:三1班 14:20—14:40 学校操场
第二场:三2班 ( )—15:10
第三场:三3班 ( )—( )
第四场:三4班 15:50—( )
(2)足球比赛项目,每两个班都要踢一场,一共踢( )场,请你在下面用画图的方式表示出踢的次数。
22.文具店里有3种不同的书包,4种不同的文具盒,妈妈要给小明买一个书包和一个文具盒,有多少种不同的买法?
23.刺绣是针线在织物上绣制各种装饰图案的总称,在中国至少有三千年的历史,主要有苏绣、湘绣、蜀绣和粤绣四大门类。下面是一家刺绣店的几款刺绣。
(1)如果买两个不同的绣屏,有几种不同的买法?
(2)如果买一个荷花绣屏和一个锦鲤绣屏,一共要付多少元?
24.小雪准备购买早餐,早餐饮品和主食织能各逃择一种。
(1)共有多少种早餐搭配方案?
(2)小雪只带了5元钱,她买了一称牛奶,剩下的钱够买一根油条吗?
25.小甲和小乙两人进行围棋赛,谁先胜三局就赢得比赛,如果最后小甲获胜了,那么比赛的过程有多少种可能?
参考答案:
1.见详解
【分析】先全部付10元的人民币得5张,然后10元人民币张数逐渐减少,5元人民币张数增加,注意10元减少1张,5元得增加2张,但5元人民币不得超过5张,据此列表即可解答
【详解】
方案 10元 5元 总钱数
① 5张 0张 50元
② 4张 2张 50元
③ 3张 4张 50元
一共有3种方式,我喜欢付5张10元,这样简单。
【点睛】不管哪种方式,付出10元和5元面值的人民币钱数和等于50元,这是解答本题的关键。
2.12种
【分析】仔细读题,已知条件“一列高铁在苏州与南京之间往返行驶”,说明苏州和南京分别是起点与终点,加上中间停靠2站,此路线共有4站,如下左图可得出答案。
【详解】由题意及分析得:要准备车票3+2+1=6(种)。还要考虑“往返”,准备的车票应是6×2=12(种)。
答:高铁站共需准备12种不同车票。
【点睛】本题主要考查的是搭配问题,解题的关键是熟练运用每种搭配,确保不遗漏每一次搭配,进而得出答案。
3.(1)14种;
(2)90种;
(3)63种
【分析】(1)若从这些书中任取一本,可以有3类办法:第一类办法是从3本不同的数学书任取一本,有3种取法;同理,从5本不同的语文书取一本有5种取法;从6本不同的英语书取一本有6种取法,这样一共有3+5+6=14(种);
(2)若从这书中取数学书、语文书、英语书各一本,需要分成三个步骤完成,第一步取1本数学书,有3种取法;第二步取1本语文书,有5种取法;第三步取1本英语书,有6种取法,根据乘法原理共有:3×5×6=90(种)取法;
(3)若是从这些书中取不同科目的两本,可以有3类办法:第一类办法是数学书、语文书各取一本,需要两个步骤,有3×5=15种方法;第二类办法取数学书和英语书各取一本,需要两个步骤,有3×6=18种方法;第三类办法取语文书和英语书各取一本,需要两个步骤,有5×6=30种方法;一共有30+15+18=63(种)。
【详解】由分析得,
(1)3+5+6
=8+6
=14(种)
答:若从这些书中任取一本,有14种不同的取法。
(2)3×5×6
=15×6
=90(种)
答:若从这书中取数学书、语文书、英语书各一本,有90种不同的取法
(3)语英:5×6=30(种)
语数:5×3=15(种)
英数:3×6=18(种)
总:30+15+18
=45+18
=63(种)
答:若是从这些书中取不同科目的两本,有63种不同的取法。
【点睛】此题考查的是排列组合,解答此题关键是为了做到不遗漏不重复,按一定顺序排列组合。
4.5元2张,2元3张或者2元8张;有两种情况。
【分析】纸币只有5元和2元,16元里有几个5元和几个2元的组合,分贝列举出来即可。
【详解】情况一:5元2张,2元3张;
5×2+2×3
=10+6
=16(元)
情况二:2元8张;
2×8=16(元)
答:可以付2张5元,3张2元;或8张2元的;有2种情况。
【点睛】解答此题的关键是分别列举出情况。
5.10种
【分析】从济南出发有4种单程票;
从济南西出发有3种单程票;
从德州东出发有2种单程票;
从沧州西出发1种单程票;
因此将这些单程票的种类加起来即可。
【详解】4+3+2+1=10(种)
答:铁路部门要为这趟列车准备10种单程车票。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
6.6套
【分析】根据题意,用画图连线的形式表示出裤子和上衣,连线表示一种穿法,数出连线数即可。
【详解】搭配方式如图:
由图可知总共有6套不同的穿法。
答:小丑有6套不同的穿法。
【点睛】本题为典型的搭配问题,用图示方法个人能够容易理解搭配问题的解法。
7.图见详解过程;8
【分析】根据题意,A与E、F有2种方案,B与E、F有2种方案,C与E、F有2种方案,D与E、F有2种方案,一共有4×2=8种选择方案,据此解答即可。
【详解】如图所示:
4×2=8(种)
答:共有8种不同的选择方案。
【点睛】乘法原理:即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法……,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×……×Mn种不同的方法。
8.三种
【分析】已知总共只有62元,需要买3份,则需要满足三份的价钱不超过62元即可,以此列出有几种可能。
【详解】19×3=57<62,所以第一种最多买3份
21×3=63>62,所以第二种最多买2份
综合上述可得到以下几种方案:①第一种3份;②第一种2份、第二种1份;③第一种1份、第2种两份。所以62元买3份有三种买法。
答:62元买3份有三种买法。
【点睛】本题考查数量运算解决实际问题,明确两种不同套餐最多/少买几份是解答此题的关键。
9.见详解
【分析】当第1个字是芝时,还可以组成芝麻门开、芝开麻门、芝开门麻、芝门麻开、芝门开麻;同理可以写出第1个字是麻、开或门的组成暗语,据此即可解答。
【详解】根据分析可得:
芝麻门开、芝开麻门、芝开门麻、芝门麻开、芝门开麻;
麻芝开门、麻芝门开、麻开芝门、麻开门芝、麻门芝开、麻门开芝;
开芝麻门、开芝门麻、开麻芝门、开麻门芝、开门麻芝、开门芝麻;
门芝麻开、门芝开麻、门麻芝开、门麻开芝、门开芝麻、门开麻芝。
【点睛】本题主要考查学生对搭配知识的掌握和灵活运用。
10.(1)9种
(2)6种
(3)11.4元
【分析】(1)小军要选一份荤菜和一份,菜单中荤菜共3种,青菜也是3种,共有3×3=9(种)不同的选菜方法;
(2)将每一种搭配按照价钱算出来与15元进行比较即可知道总价不超过15元的有多少种选法;
(3)根据第二问直接得到最便宜的搭配方法。
【详解】(1)3×3=9(种)
答:他有9种不同的选菜方法。
(2)熏干芹菜+宫保鸡丁=3.8+8.8=12.6(元)<15元;
熏干芹菜+炸肉串=3.8+9.5=13.3(元)<15元;
熏干芹菜+炖排骨=3.8+12.6=16.4(元);
炒胡萝卜+宫保鸡丁=3.2+8.8=12(元)<15元;
炒胡萝卜+炸肉串=3.2+9.5=12.7(元)<15元;
炒胡萝卜+炖排骨=3.2+12.6=15.8(元);
烧茄子+宫保鸡丁=2.6+8.8=11.4(元)<15元;
烧茄子+炸肉串=2.6+9.5=12.1(元)<15元;
烧茄子+炖排骨=2.6+12.6=15.2(元);
答:总价不超过15元的有6种选法。
(3)最便宜的为烧茄子+宫保鸡丁=2.6+8.8=11.4(元)
答:最便宜的搭配要花11.4元。
【点睛】本题考查的是简单的搭配问题,关键是注意搞清楚搭配,做到不重不漏。
11.6;画图见详解
【分析】根据搭配的方法进行两两连线,应依次连线,避免遗漏,但是又不能重复。
【详解】
如图所示,小明想从中任选两本书,一共有6种不同的选法。
【点睛】熟练掌握搭配问题的计算是解答此题的关键。
12.55场;52场;136场
【分析】单循环赛制的场数=队伍数×(队伍数-1)÷2,根据这个公式分别计算;注意第二种情况下,三组各有两队不需要再比赛,因此要减少3场比赛。
【详解】6×(6-1)÷2×2+5×(5-1)÷2
=6×5÷2×2+5×4÷2
=30+10
=40(场)
40+6×(6-1)÷2
=40+6×5÷2
=40+15
=55(场)
55-3=52(场)
17×(17-1)÷2
=17×16÷2
=136(场)
答:第一种情况共需要55场;第二种情况共需要52场;第三种情况共需要136场。
【点睛】本题考查排列组合的知识,关键是掌握循环赛问题的求解方法。
13.6种
【分析】每个人都可以和其他的1个人一起表演节目,即两两组合,据此列举即可。
【详解】如图:
①和②、①和③、①和④、②和③、②和④、③和④;
所以共有6种不同的选法。
答:共有6种选法;①和②、①和③、①和④、②和③、②和④、③和④。
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果人比较少可以用枚举法解答,如果人比较多可以用公式:握手次数解答。
14.4种
【分析】根据题意,4个人的位置按题目要求排列,列举出所有情况,得出结论。
【详解】4个人的不同站法如下:
①小明、爸爸、妈妈、妹妹;
②小明、妈妈、爸爸、妹妹;
③妹妹、爸爸、妈妈、小明;
④妹妹、妈妈、爸爸、小明;
答:一共有4种不同的站法。
【点睛】也可以用乘法原理解答,爸爸、妈妈站中间位置,有2种选择;小明、妹妹站两边位置,也有2种选择;一共有2×2=4种不同的站法。
15.(1)0.268、0.286、0.628、0.682、0.826、0.862
(2)8.062、8.026、8.620、8.602、8.260、8.206
【分析】(1)整数部分只能是0,剩下3个数字都在小数部分,列举即可。
(2)要求大于8,这四个数字中,最大的就是8,小数部分又是三位数的小数,所以整数部分是8,其余在小数部分,列举即可。
【详解】(1)小于1而小数部分是三位小数:0.268、0.286、0.628、0.682、0.826、0.862。
(2)大于8而小数部分是三位的小数:8.062、8.026、8.620、8.602、8.260、8.206。
【点睛】本题考查了排列组合知识的灵活应用,关键是确定整数部分。
16.6种
【分析】先考虑第1次有多少种传法?然后用树形图画出每次传球后给谁。要注意只有第4次传球后回到小手上的才是符合题意的传法。
【详解】由题意可知,小先拿球,则第1次可以给莫也可以给萱。
由题意画树形图如下:
由图可知,共有6种情况符合要求。
答:一共有6种不同的传球过程。
【点睛】根据题意分析出第1次只能给莫或萱,据此正确画出树形图是解题关键。
17.2种
【分析】可以先考虑第1个位置可以站哪些小动物?再考虑第2个位置。以第一个位置站的小动物为“树根”,画出树形图,即可得到所有的站法。
【详解】由题意,画树形图如下:
由图可知,有2种不同的站法。
答:它们共有2种不同的站法。
【点睛】树形图是枚举法的一种,可以使我们的枚举过程更加直观,有条理又不易重复或遗漏。
18.5种
【分析】根据题意,小高第一步可以走到2号地毯或3号地毯,据此注意分析即可,注意题目中的限定条件:相邻编号地毯和只能向右走,另外只有结束在5号地毯的才符合题意。
【详解】根据题意,画图如下:
数一数可知,一共5种可能。
答:小高一共有5种不同的走法。
【点睛】解答此类问题,按照树形图的画法逐一画出所有的分叉即可。注意不重复不遗漏。
19.(1)密码可能是:25、27、52、57、72、75,从小到大排列为:25<27<52<57<72<75;
(2)25,根据题意可知,这组两位数按照以上的排列顺序不断重复出现,每六个数是一组,145除以6,总共出现了24组,余下一个数,即这个数的密码就是第一个数为25
【分析】(1)先将组成的两位数依次写出来,分别由25、52、57、75、27、72,然后按照数的大小依次排列即可;(2)根据题意可知,这组两位数按照以上的排列顺序不断重复的,每六个数是一组,用145除以6,会发现共有24组,余下一个数就是第145个数为25,据此解答。
【详解】(1)密码可能是哪个数?请把它们全部写出来,并把这些数按照从小到大的顺序排列。
答:组成没有重复的两位数:25、27、52、57、72、75;从小到大的顺序排列为:25<27<52<57<72<75。
(2)如果这组两位数按照以上的排列顺序不断重复出现,第145个数就是这只宝箱的密码,这个密码是什么数?(请写出你的思考过程。)
根据题意可知,这组两位数按照以上的排列顺序不断重复出现,每六个数是一组,145除以6,总共出现了24组,余下一个数,即这个数的密码就是第一个数为25。
【点睛】熟练掌握根据给出的数字组成没有重复的数字的方法是解答本题的关键。
20.9;见详解
【分析】每种主食都可以和每种粥搭配在一起,则小米粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。绿豆粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。蔬菜粥分别和馒头、面包、豆沙包搭配一起,有3种搭配方法。则一共能3+3+3=9种不同的搭配方法。
【详解】早餐时,粥和主食各取一种,共有9种不同的搭配方法。
【点睛】本题考查搭配问题,采用枚举法解答。
21.(1)14:50;15:20;15:40;16:10;
(2)6;图见详解
【分析】(1)经过的时间等于结束的时间减去开始的时间即可;
(2)根据题意,每两个班都要踢一次,画出一个长方形,再画出它的对角线,四个角标出1~4,就是所踢的次数,据此解答。
【详解】(1)花样跳绳比赛14:20开始,每场比赛20分钟,准备10分钟。请你把表格里的比赛时间补充完整。
场次及班级 时间 地点
第一场:三1班 14:20—14:40 学校操场
第二场:三2班 (14:50)—15:10
第三场:三3班 (15:20)—(15:40)
第四场:三4班 15:50—(16:10)
(2)足球比赛项目,每两个班都要踢一场,一共踢(6)场,请你在下面用画图的方式表示出踢的次数。
【点睛】本题主要考查时间和日期以及握手问题,熟练掌握并灵活运用。
22.12种
【分析】妈妈要给小明买一个书包和一个文具盒,从3种不同的书包中选1种,有3种选法;从4种不同的文具盒中选1种,有4种选法;根据乘法原理共有3×4=12(种)不同的买法。
【详解】根据分析得:
3×4=12(种)
答:有12种不同的买法。
【点睛】做这类搭配类题目时,我们要做到有序、不重复、不遗漏。所以一定要按照一定顺序来思考问题才能考虑周全。
23.(1)6种;(2)93.2元
【分析】(1)如果买两个不同的绣屏,就相当于4选2,根据握手问题的计算方法:握手次数=人数×(人数-1)÷2,代入数据计算即可。
(2)求买一个荷花绣屏和一个锦鲤绣屏,一共要付多少元,把两种物品的单价相加即可。
【详解】(1)4×(4-1)÷2
=4×3÷2
=12÷2
=6(种)
答:如果买两个不同的绣屏,有6种不同的买法。
(2)23.7+69.5=93.2(元)
答:如果买一个荷花绣屏和一个锦鲤绣屏,一共要付93.2元。
【点睛】本题考查了握手问题的实际应用,要注意去掉重复计算的情况,如果数量比较少可以用枚举法解答,如果数量比较多可以用公式:握手次数=人数×(人数-1)÷2解答解答。
24.(1)6种;(2)够
【分析】(1)用饮料的种类乘主食的种类,可以计算出共有多少种早餐搭配方案。
(2)用小雪带的钱数减去牛奶的钱数,可以计算出剩余的钱数,再用剩余的钱数与油条的钱数比较即可。
【详解】(1)2×3=6(种)
答:共有6种早餐搭配方案。
(2)5-2.8=2.2(元)
2.2>2
答:剩下的钱够买一根油条。
【点睛】本题解题关键是熟练掌握搭配原理的计算方法,再根据小数减法的意义列式计算。
25.10种
【分析】试着把每场比赛的结果用树形图表示出来。注意:不会有“小乙-小甲-小乙-小乙-小甲”这样的过程出现,因为这种情况下,塞完第4场后小乙已经获胜,不合题意。
【详解】第一场小甲胜时:
第一场小乙胜时:
综上,共有10种可能。
答:比赛的过程有10种可能。
【点睛】树形图是枚举法的一种,可以使我们的枚举过程更加直观,有条理又不易重复或遗漏。
26.2种
【分析】首先根据题意,甲、丁都不站在第1个,所以第1个只能是乙或者丙,以此为“树根”,画树形图解答即可。
【详解】由题意可知:第1个只能是乙或者丙。
第1个是乙时:
第1个是丙时:
综上,一共有2种。
答:一共有2种不同的站队方法。
【点睛】树形图是枚举法的一种,画树状图的关键一是确定层数,二是确定每层分叉的个数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
