小升初知识点分类汇编(北京)-07平面图形(试题)-六年级数学下册北京版(含解析)
文档属性
| 名称 | 小升初知识点分类汇编(北京)-07平面图形(试题)-六年级数学下册北京版(含解析) | 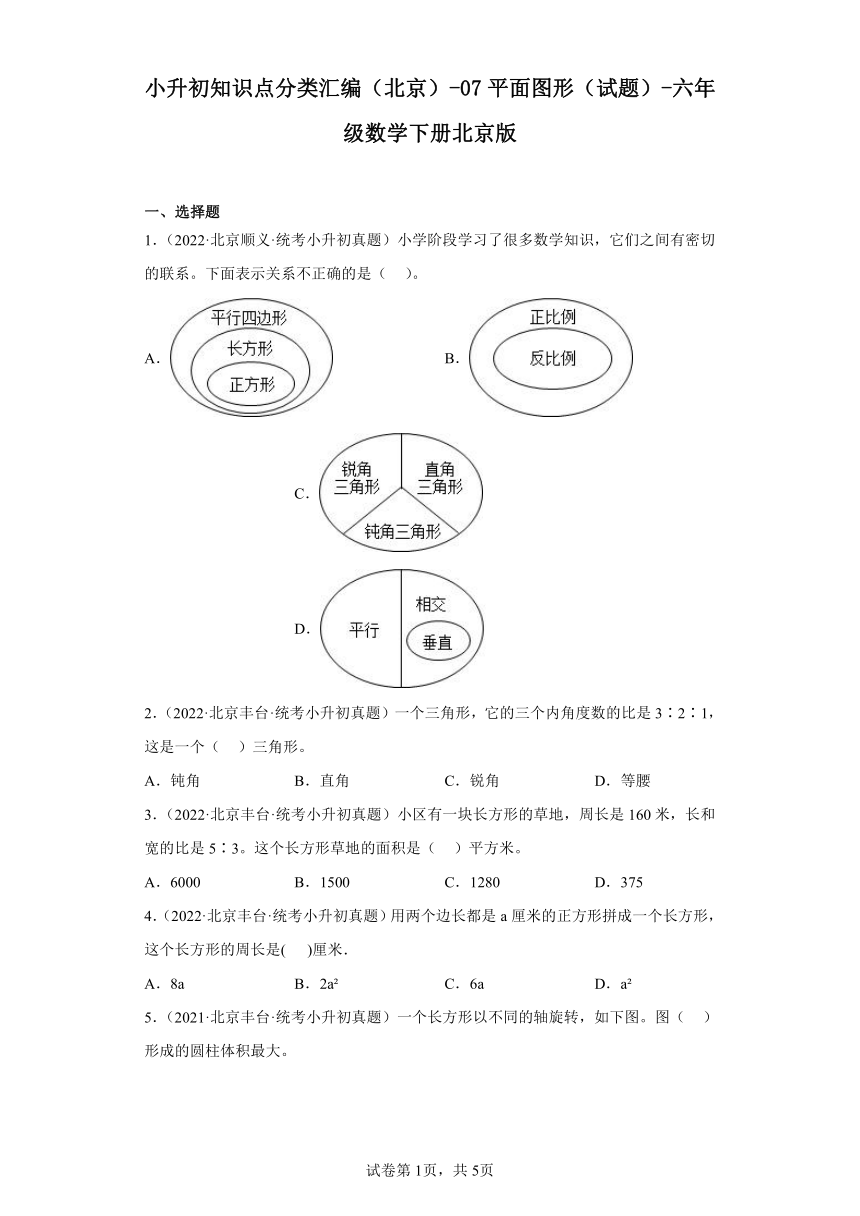 | |
| 格式 | doc | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 11:05:07 | ||
图片预览



文档简介
小升初知识点分类汇编(北京)-07平面图形(试题)-六年级数学下册北京版
一、选择题
1.(2022·北京顺义·统考小升初真题)小学阶段学习了很多数学知识,它们之间有密切的联系。下面表示关系不正确的是( )。
A. B. C. D.
2.(2022·北京丰台·统考小升初真题)一个三角形,它的三个内角度数的比是3∶2∶1,这是一个( )三角形。
A.钝角 B.直角 C.锐角 D.等腰
3.(2022·北京丰台·统考小升初真题)小区有一块长方形的草地,周长是160米,长和宽的比是5∶3。这个长方形草地的面积是( )平方米。
A.6000 B.1500 C.1280 D.375
4.(2022·北京丰台·统考小升初真题)用两个边长都是a厘米的正方形拼成一个长方形,这个长方形的周长是( )厘米.
A.8a B.2a C.6a D.a
5.(2021·北京丰台·统考小升初真题)一个长方形以不同的轴旋转,如下图。图( )形成的圆柱体积最大。
A. B. C. D.
6.(2021·北京丰台·统考小升初真题)下面每组数是三根小棒的长度,用它们不能首尾相接拼成一个三角形的是( )。
A.6、6、l B.5、7、2 C.5、6、9 D.5、6、5
7.(2020·北京大兴·统考小升初真题)一个圆柱侧面展开后是正方形,这个圆柱的底面半径与高的比为( )。
A.π∶1 B.1∶2π C.1∶1 D.2π∶1
8.(2020·北京大兴·统考小升初真题)一个三角形,三个内角度数的比是1∶2∶3,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
9.(2020·北京大兴·统考小升初真题)两个完全一样的梯形可以拼成一个平行四边形。拼好的平行四边形底是16厘米,高是10厘米。其中一个梯形的面积是( )平方厘米。
A.320 B.160 C.80 D.40
10.(2020·北京顺义·统考小升初真题)三角形三个内角的度数比是2∶4∶3,这个三角形是( )。
A.钝角三角形 B.锐角三角形 C.等边三角形 D.等腰三角形
二、填空题
11.(2022·北京昌平·统考小升初真题)小明用圆规在纸上画一个周长是12.56厘米的圆。这时圆规两脚间的距离是( )厘米。
12.(2022·北京丰台·统考小升初真题)用长4厘米,宽3厘米的长方形密铺成一个正方形,至少需要( )个这样的长方形。
13.(2022·北京丰台·统考小升初真题)春天来了,明明和爸爸骑着不同型号(如图)的脚踏车去郊游。明明和爸爸脚踏车车轮分别转动一周前进距离的比是( )。
14.(2021·北京丰台·统考小升初真题)小圆半径是大圆半径的,小圆与大圆的周长比是( )。
15.(2020·北京大兴·统考小升初真题)下图中长方形的长是20厘米,涂色部分的面积是( )平方厘米。
16.(2020·北京昌平·统考小升初真题)观察下图:小蜗牛后面藏的四边形可能是( )。
17.(2020·北京昌平·统考小升初真题)把圆规两脚叉开2厘米画圆,所画出的圆半径是( )厘米,面积是( )平方厘米。
18.(2020·北京顺义·统考小升初真题)一块长方形草地的周长是160米,长和宽的比是5∶3,草地的面积是( )平方米。
三、解答题
19.(2022·北京顺义·统考小升初真题)按要求画图。
①图中每个小方格的边长是1厘米,在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形,这个三角形的面积是( )平方厘米。
②按照2∶1的比,在方格纸中画出三角形ABC放大后的三角形,它的面积是( )平方厘米。
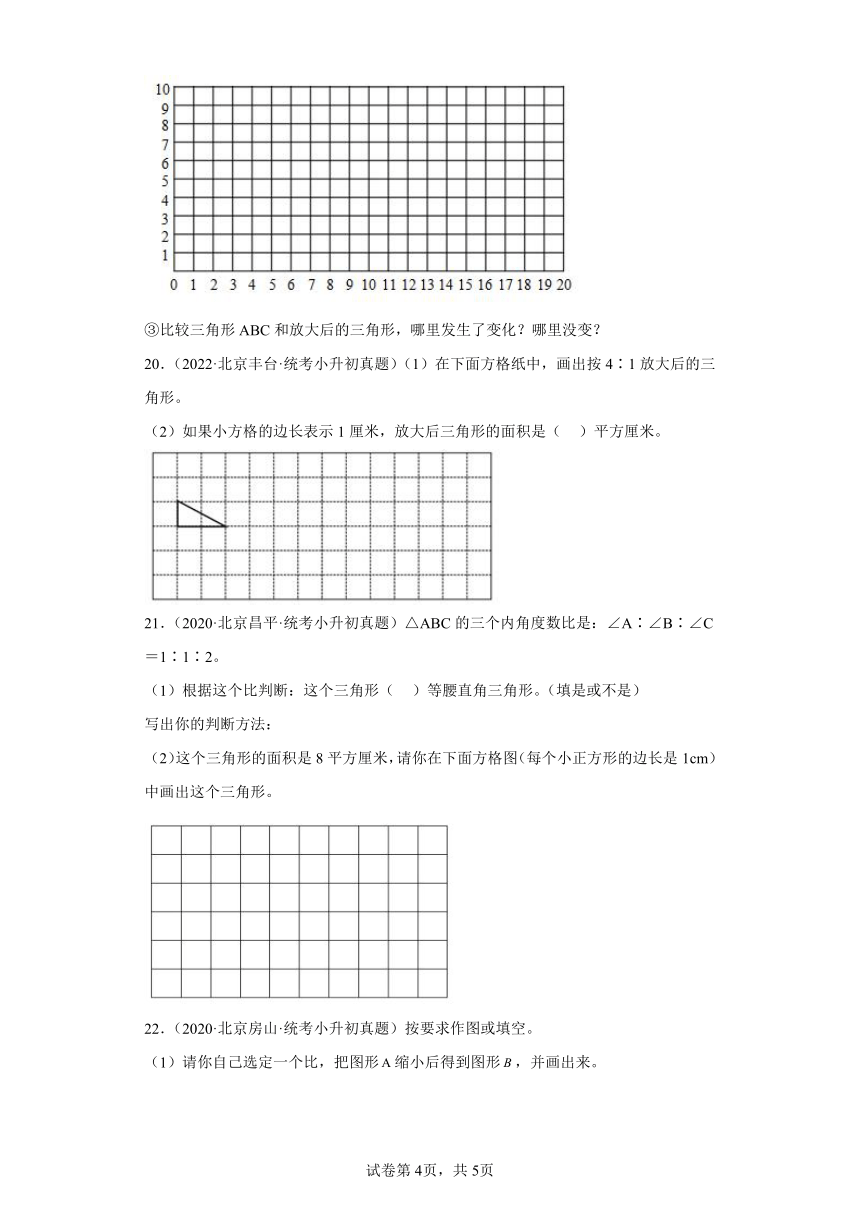
③比较三角形ABC和放大后的三角形,哪里发生了变化?哪里没变?
20.(2022·北京丰台·统考小升初真题)(1)在下面方格纸中,画出按4∶1放大后的三角形。
(2)如果小方格的边长表示1厘米,放大后三角形的面积是( )平方厘米。
21.(2020·北京昌平·统考小升初真题)△ABC的三个内角度数比是:∠A∶∠B∶∠C=1∶1∶2。
(1)根据这个比判断:这个三角形( )等腰直角三角形。(填是或不是)
写出你的判断方法:
(2)这个三角形的面积是8平方厘米,请你在下面方格图(每个小正方形的边长是1cm)中画出这个三角形。
22.(2020·北京房山·统考小升初真题)按要求作图或填空。
(1)请你自己选定一个比,把图形缩小后得到图形,并画出来。
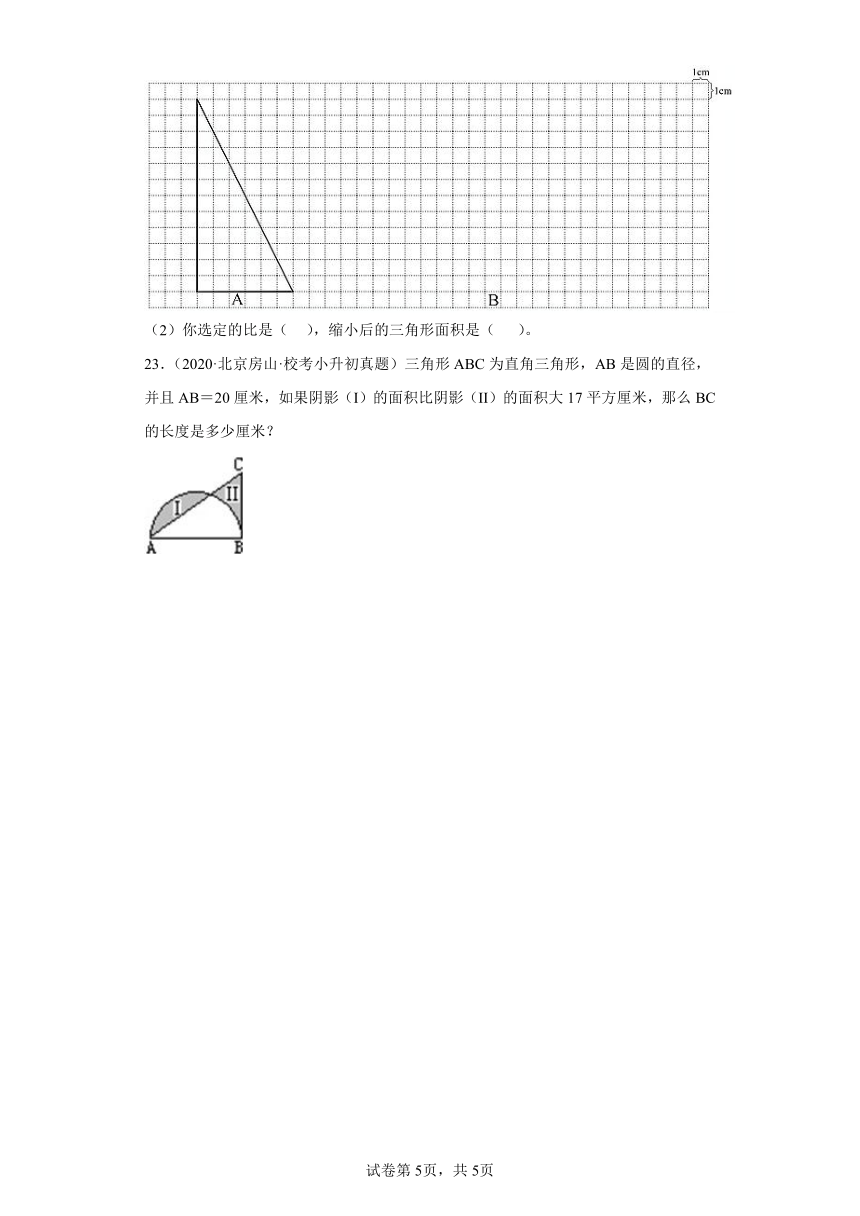
(2)你选定的比是( ),缩小后的三角形面积是( )。
23.(2020·北京房山·校考小升初真题)三角形ABC为直角三角形,AB是圆的直径,并且AB=20厘米,如果阴影(I)的面积比阴影(II)的面积大17平方厘米,那么BC的长度是多少厘米?
参考答案:
1.B
【分析】A.正方形是特殊的长方形,正方形和长方形都是特殊的平行四边形,据此分析;
B.x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析;
C.三角形按角分类,可以分成锐角三角形、直角三角形、钝角三角形,据此分析;
D.同一平面内,两条直线除了平行就是相交,两条直线相交成直角时,这两条直线相互垂直,据此分析。
【详解】A.,关系表示正确;
B. 正比例和反比例是两种不同的数量关系,关系表示错误;
C.,关系表示正确;
D.,关系表示正确。
故答案为:B
【点睛】本题考查的知识点较多,要综合运用所学知识。
2.B
【分析】三角形的内角和是180°,已知三个内角度数的比是3∶2∶1,那么总份数是(3+2+1)份,用内角和除以总份数,求出一份数,再用一份数乘3,求出三角形最大内角的度数,根据三角形的分类,得出三角形的类型。
【详解】180°÷(3+2+1)
=180°÷6
=30°
最大的内角是:30°×3=90°
这是一个直角三角形。
故答案为:B
【点睛】掌握三角形的内角和以及按比例分配的解题方法,明确要分配的总量是多少,以及按照什么比例进行分配,求出一份数是解题的关键。
3.B
【分析】周长÷2,先求出长+宽的和,长宽和÷总份数,求出一份数,一份数分别乘长和宽的对应份数,求出长和宽,再根据长方形面积=长×宽,列式计算即可。
【详解】160÷2÷(5+3)
=80÷8
=10(米)
10×5=50(米)
10×3=30(米)
50×30=1500(平方米)
故答案为:B
【点睛】关键是理解比的意义,掌握长方形面积公式。
4.C
【详解】略
5.B
【分析】假设这个长方形的长是4厘米,宽是2厘米,根据圆柱的体积=底面积×高,分别算出体积,进行比较即可选择。
【详解】假设这个长方形的长是4厘米,宽是2厘米
A.3.14×2×2×4=50.24(立方厘米)
B.3.14×4×4×2=100.48(立方厘米)
C.3.14×1×1×4=12.56(立方厘米)
D.3.14×2×2×2=25.12(立方厘米)
12.56<25.12<50.24<100.48
故答案为:B
【点睛】熟练掌握圆柱的体积公式,是解答此题的关键。
6.B
【分析】根据三角形的特性:任意两边之和大于第三边,任意两边之差小于第三边,进行分析即可。
【详解】A.因为6+1>6,所以能围成一个三角形;
B.因为5+2=7,所以不能围成一个三角形;
C.因为6+5>9,所以能围成一个三角形;
D.因为5+5>6,所以能围成一个三角形;
故答案为:B
【点睛】解答此题的关键是根据三角形的特性进行分析、解答即可。
7.B
【分析】根据题意,圆柱侧面展开后是正方形,那么这个圆柱的底面周长与高相等;由圆的周长公式C=2πr可得出,高h也等于2πr;然后根据比的意义,写出圆柱的底面半径与高的比,再化简即可。
【详解】设圆柱的底面半径是r。
因为圆柱侧面展开后是正方形,所以高=底面周长,即h=2πr。
r∶h
= r∶2πr
=1∶2π
这个圆柱的底面半径与高的比为1∶2π。
故答案为:B
【点睛】本题考查圆柱侧面展开图的特点、圆周长公式的运用、比的意义及化简比,明确圆柱侧面展开图是正方形时,圆柱的底面周长与高相等。
8.B
【分析】根据三角形内角和180°,利用按比例分配的方法求出最大角的度数,从而根据最大角的度数就能确定其形状。
【详解】180°×=90°
90°的角是直角,有一个角是直角的三角形是直角三角形。
故答案为:B
【点睛】此题主要考查学生对三角形内角和定理及三角形形状的判断的综合运用。
9.C
【分析】拼成的平行四边形面积是梯形面积的2倍,用底×高,求出平行四边形面积,除2即可。
【详解】16×10÷2=80(平方厘米)
故答案为:C
【点睛】关键是掌握梯形面积推导过程,梯形面积=(上底+下底)×高÷2。
10.B
【分析】三角形内角和180°,三个内角分别占2份、4份、3份,先求出一份数,再分别求出三个角的度数,根据三个内角度数分析是什么三角形即可。
【详解】180÷(2+4+3)
=180÷9
=20(度)
20×2=40(度)
20×4=80(度)
20×3=60(度)
三个角都是锐角,所以是锐角三角形。
故答案为:B
【点睛】本题考查了按比例分配应用题、三角形的内角和及分类,将比的各项看成份数比较好理解。
11.2
【分析】画圆时,圆规两脚间的距离就是所画圆的半径,圆的周长已知,根据圆的周长公式,代入数值计算即可求出半径。
【详解】12.56÷3.14÷2
=4÷2
=2(厘米)
【点睛】解答本题的关键是理解用圆规画圆时,圆规两脚间的距离就是所画圆的半径。
12.12
【分析】先求出正方形的边长最小是多少厘米,即求4和3的最小公倍数;然后根据求出的正方形的边长进行分析:看能放几排,几列,然后相乘即可。
【详解】4×3=12
所以4和3的最小公倍数是12
(12÷4)×(12÷3)
=3×4
=12(块)
【点睛】解决本题先理解怎么样才能拼成一个正方形,然后找出这个正方形的边长,再求几个长(几个宽)才能拼成边长,进而求解。
13.
【分析】车轮转动一圈的距离即为车轮圆的周长,根据圆的周长=,得出两个车轮的周长,在运用比的基本性质化简得到答案。
【详解】由题意可得:爸爸的脚踏车转动一圈距离为:28π英寸,明明的脚踏车车轮转动一圈的距离为:20π英寸;故明明和爸爸脚踏车车轮分别转动一周前进距离的比为:。
【点睛】本题主要考查的是圆的周长及比的应用,解题的关键是熟练掌握比的化简方法,进而得出答案。
14.3∶4
【分析】由圆的周长公式可知,圆的周长与圆的半径有关,小圆与大圆的周长比等于小圆与大圆的半径比,据此解答。
【详解】假设大圆的半径为1,则小圆的半径为。
小圆的周长∶大圆的周长=∶1=3∶4
【点睛】两个圆的半径比等于直径比等于周长比,注意比的前项和后项是解答题目的关键。
15.157
【分析】从图中可知,长方形长的一半就是圆的半径,涂色部分的面积就是半圆的面积,据圆的面积公式,即可求出图中涂色部分的面积。
【详解】20÷2=10(厘米)
3.14×(10×10)÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
【点睛】理解图中长方形长的一半就是圆的半径,涂色部分的面积就是半圆的面积,这是解决此题的关键。
16.长方形
【分析】长方形特征:对边平行且相等,4个角都是直角的四边形,据此解答。
【详解】根据长方形的特征可知,小蜗牛后面藏的四边形可能是长方形。
【点睛】掌握长方形的特征是解答此题的关键。
17. 2 12.56
【分析】圆规两脚叉开的距离即为圆半径,根据圆的面积:S=πr2即可求出面积。
【详解】圆的半径为:2厘米;
圆的面积为:3.14×22
=3.14×4
=12.56(平方厘米)。
【点睛】此题考查了圆的面积,此题应明确:圆规两脚叉开的距离即为圆半径。
18.1500
【分析】先求出一组长和宽的和,长是5份,宽是3份,用长和宽的和÷(5+3),求出一份数,据此求出长和宽,再根据长方形的面积公式计算即可。
【详解】160÷2÷(5+3)
=80÷8
=10(米)
10×5=50(米)
10×3=30(米)
50×30=1500(平方米)
故答案为:1500
【点睛】本题考查了按比例分配应用题和长方形的周长及面积,长方形周长=(长+宽)×2,长方形面积=长×宽。
19.①见详解;9
②见详解;36
③见详解
【分析】①用数对表示位置,数对的第一个数表示列,第二个数表示行;在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形;再根据三角形的面积=底×高÷2,求出这个三角形的面积。
②把三角形ABC的各边按2∶1的比放大,再根据三角形的面积公式求出放大后的三角形的面积。
③图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】①三角形ABC的底是6厘米,高是3厘米;
三角形ABC的面积是:
6×3÷2
=18÷2
=9(平方厘米)
②放大后的三角形的底是:6×2=12(厘米)
放大后的三角形的高是:3×2=6(厘米)
放大后三角形的面积是:
12×6÷2
=72÷2
=36(平方厘米)
如图:
③比较三角形ABC和放大后的三角形,大小发生了变化,形状没变。
【点睛】掌握根据数对找位置、三角形的面积的计算、作放大后的图形以及图形放大的特点是解题的关键。
20.(1)见详解(2)16
【分析】(1)观图可知:三角形的两条直角边是1和2,按4∶1的比画出扩大后的三角形的两条直角边分别是1×4=4(厘米),2×4=8(厘米),据此即可画图;
(2)根据三角形的面积S=ah÷2,代入数据解答即可。
【详解】(1)1×4=4(厘米)
2×4=8(厘米)
作图如下:
(2)4×8÷2
=32÷2
=16(平方厘米)
【点睛】此题考查了图形的放大与缩小及三角形面积公式的应用。
21.(1)是;因为最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等。
(2)
【分析】(1)根据∠A∶∠B∶∠C=1∶1∶2,可知最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等,所以这个三角形是等腰直角三角形。
(2)三角形的面积=底×高÷2,那么底×高=三角形的面积×2,根据(1)可知这个三角形是等腰直角三角形,那么底和高相等,进而求出腰长,据此画图。
【详解】略
22.(1)
(2)1∶3;4平方厘米
【分析】图形缩小的意义:图形按照一定比例变小,但形状没有发生变化。
【详解】原图形底为6 cm,高为12 cm。
按1∶3缩小,缩小后底为:(cm),高为:(cm)
缩小后面积为:2×4×=8×=4(cm2)
【点睛】选定的缩小的比的后项,得是原图形的底和高的公因数。这样原图形的底和高才能被比的后项整除,得到整数长的底和高。
23.14厘米
【分析】阴影(I)的面积比阴影(II)的面积大17平方厘米,也就是半圆的面积比三角形ABC的面积大17平方厘米,据此可知本题的数量的关系:半圆面积﹣三角形ABC面积=17,据此数量关系可列方程解答。
【详解】解:设BC长x厘米,根据题意得:
3.14×(20÷2)2÷2﹣20x÷2=17
3.14×100÷2﹣10x=17
157﹣10x=17
157﹣17=10x
10x=140
x=14
答:BC的长度是14厘米。
【点睛】本题的关键是根据半圆的面积比三角形ABC的面积大17平方厘米,找出数量关系,再列方程解答。
试卷第1页,共3页
试卷第1页,共3页
一、选择题
1.(2022·北京顺义·统考小升初真题)小学阶段学习了很多数学知识,它们之间有密切的联系。下面表示关系不正确的是( )。
A. B. C. D.
2.(2022·北京丰台·统考小升初真题)一个三角形,它的三个内角度数的比是3∶2∶1,这是一个( )三角形。
A.钝角 B.直角 C.锐角 D.等腰
3.(2022·北京丰台·统考小升初真题)小区有一块长方形的草地,周长是160米,长和宽的比是5∶3。这个长方形草地的面积是( )平方米。
A.6000 B.1500 C.1280 D.375
4.(2022·北京丰台·统考小升初真题)用两个边长都是a厘米的正方形拼成一个长方形,这个长方形的周长是( )厘米.
A.8a B.2a C.6a D.a
5.(2021·北京丰台·统考小升初真题)一个长方形以不同的轴旋转,如下图。图( )形成的圆柱体积最大。
A. B. C. D.
6.(2021·北京丰台·统考小升初真题)下面每组数是三根小棒的长度,用它们不能首尾相接拼成一个三角形的是( )。
A.6、6、l B.5、7、2 C.5、6、9 D.5、6、5
7.(2020·北京大兴·统考小升初真题)一个圆柱侧面展开后是正方形,这个圆柱的底面半径与高的比为( )。
A.π∶1 B.1∶2π C.1∶1 D.2π∶1
8.(2020·北京大兴·统考小升初真题)一个三角形,三个内角度数的比是1∶2∶3,这个三角形是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
9.(2020·北京大兴·统考小升初真题)两个完全一样的梯形可以拼成一个平行四边形。拼好的平行四边形底是16厘米,高是10厘米。其中一个梯形的面积是( )平方厘米。
A.320 B.160 C.80 D.40
10.(2020·北京顺义·统考小升初真题)三角形三个内角的度数比是2∶4∶3,这个三角形是( )。
A.钝角三角形 B.锐角三角形 C.等边三角形 D.等腰三角形
二、填空题
11.(2022·北京昌平·统考小升初真题)小明用圆规在纸上画一个周长是12.56厘米的圆。这时圆规两脚间的距离是( )厘米。
12.(2022·北京丰台·统考小升初真题)用长4厘米,宽3厘米的长方形密铺成一个正方形,至少需要( )个这样的长方形。
13.(2022·北京丰台·统考小升初真题)春天来了,明明和爸爸骑着不同型号(如图)的脚踏车去郊游。明明和爸爸脚踏车车轮分别转动一周前进距离的比是( )。
14.(2021·北京丰台·统考小升初真题)小圆半径是大圆半径的,小圆与大圆的周长比是( )。
15.(2020·北京大兴·统考小升初真题)下图中长方形的长是20厘米,涂色部分的面积是( )平方厘米。
16.(2020·北京昌平·统考小升初真题)观察下图:小蜗牛后面藏的四边形可能是( )。
17.(2020·北京昌平·统考小升初真题)把圆规两脚叉开2厘米画圆,所画出的圆半径是( )厘米,面积是( )平方厘米。
18.(2020·北京顺义·统考小升初真题)一块长方形草地的周长是160米,长和宽的比是5∶3,草地的面积是( )平方米。
三、解答题
19.(2022·北京顺义·统考小升初真题)按要求画图。
①图中每个小方格的边长是1厘米,在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形,这个三角形的面积是( )平方厘米。
②按照2∶1的比,在方格纸中画出三角形ABC放大后的三角形,它的面积是( )平方厘米。
③比较三角形ABC和放大后的三角形,哪里发生了变化?哪里没变?
20.(2022·北京丰台·统考小升初真题)(1)在下面方格纸中,画出按4∶1放大后的三角形。
(2)如果小方格的边长表示1厘米,放大后三角形的面积是( )平方厘米。
21.(2020·北京昌平·统考小升初真题)△ABC的三个内角度数比是:∠A∶∠B∶∠C=1∶1∶2。
(1)根据这个比判断:这个三角形( )等腰直角三角形。(填是或不是)
写出你的判断方法:
(2)这个三角形的面积是8平方厘米,请你在下面方格图(每个小正方形的边长是1cm)中画出这个三角形。
22.(2020·北京房山·统考小升初真题)按要求作图或填空。
(1)请你自己选定一个比,把图形缩小后得到图形,并画出来。
(2)你选定的比是( ),缩小后的三角形面积是( )。
23.(2020·北京房山·校考小升初真题)三角形ABC为直角三角形,AB是圆的直径,并且AB=20厘米,如果阴影(I)的面积比阴影(II)的面积大17平方厘米,那么BC的长度是多少厘米?
参考答案:
1.B
【分析】A.正方形是特殊的长方形,正方形和长方形都是特殊的平行四边形,据此分析;
B.x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,据此分析;
C.三角形按角分类,可以分成锐角三角形、直角三角形、钝角三角形,据此分析;
D.同一平面内,两条直线除了平行就是相交,两条直线相交成直角时,这两条直线相互垂直,据此分析。
【详解】A.,关系表示正确;
B. 正比例和反比例是两种不同的数量关系,关系表示错误;
C.,关系表示正确;
D.,关系表示正确。
故答案为:B
【点睛】本题考查的知识点较多,要综合运用所学知识。
2.B
【分析】三角形的内角和是180°,已知三个内角度数的比是3∶2∶1,那么总份数是(3+2+1)份,用内角和除以总份数,求出一份数,再用一份数乘3,求出三角形最大内角的度数,根据三角形的分类,得出三角形的类型。
【详解】180°÷(3+2+1)
=180°÷6
=30°
最大的内角是:30°×3=90°
这是一个直角三角形。
故答案为:B
【点睛】掌握三角形的内角和以及按比例分配的解题方法,明确要分配的总量是多少,以及按照什么比例进行分配,求出一份数是解题的关键。
3.B
【分析】周长÷2,先求出长+宽的和,长宽和÷总份数,求出一份数,一份数分别乘长和宽的对应份数,求出长和宽,再根据长方形面积=长×宽,列式计算即可。
【详解】160÷2÷(5+3)
=80÷8
=10(米)
10×5=50(米)
10×3=30(米)
50×30=1500(平方米)
故答案为:B
【点睛】关键是理解比的意义,掌握长方形面积公式。
4.C
【详解】略
5.B
【分析】假设这个长方形的长是4厘米,宽是2厘米,根据圆柱的体积=底面积×高,分别算出体积,进行比较即可选择。
【详解】假设这个长方形的长是4厘米,宽是2厘米
A.3.14×2×2×4=50.24(立方厘米)
B.3.14×4×4×2=100.48(立方厘米)
C.3.14×1×1×4=12.56(立方厘米)
D.3.14×2×2×2=25.12(立方厘米)
12.56<25.12<50.24<100.48
故答案为:B
【点睛】熟练掌握圆柱的体积公式,是解答此题的关键。
6.B
【分析】根据三角形的特性:任意两边之和大于第三边,任意两边之差小于第三边,进行分析即可。
【详解】A.因为6+1>6,所以能围成一个三角形;
B.因为5+2=7,所以不能围成一个三角形;
C.因为6+5>9,所以能围成一个三角形;
D.因为5+5>6,所以能围成一个三角形;
故答案为:B
【点睛】解答此题的关键是根据三角形的特性进行分析、解答即可。
7.B
【分析】根据题意,圆柱侧面展开后是正方形,那么这个圆柱的底面周长与高相等;由圆的周长公式C=2πr可得出,高h也等于2πr;然后根据比的意义,写出圆柱的底面半径与高的比,再化简即可。
【详解】设圆柱的底面半径是r。
因为圆柱侧面展开后是正方形,所以高=底面周长,即h=2πr。
r∶h
= r∶2πr
=1∶2π
这个圆柱的底面半径与高的比为1∶2π。
故答案为:B
【点睛】本题考查圆柱侧面展开图的特点、圆周长公式的运用、比的意义及化简比,明确圆柱侧面展开图是正方形时,圆柱的底面周长与高相等。
8.B
【分析】根据三角形内角和180°,利用按比例分配的方法求出最大角的度数,从而根据最大角的度数就能确定其形状。
【详解】180°×=90°
90°的角是直角,有一个角是直角的三角形是直角三角形。
故答案为:B
【点睛】此题主要考查学生对三角形内角和定理及三角形形状的判断的综合运用。
9.C
【分析】拼成的平行四边形面积是梯形面积的2倍,用底×高,求出平行四边形面积,除2即可。
【详解】16×10÷2=80(平方厘米)
故答案为:C
【点睛】关键是掌握梯形面积推导过程,梯形面积=(上底+下底)×高÷2。
10.B
【分析】三角形内角和180°,三个内角分别占2份、4份、3份,先求出一份数,再分别求出三个角的度数,根据三个内角度数分析是什么三角形即可。
【详解】180÷(2+4+3)
=180÷9
=20(度)
20×2=40(度)
20×4=80(度)
20×3=60(度)
三个角都是锐角,所以是锐角三角形。
故答案为:B
【点睛】本题考查了按比例分配应用题、三角形的内角和及分类,将比的各项看成份数比较好理解。
11.2
【分析】画圆时,圆规两脚间的距离就是所画圆的半径,圆的周长已知,根据圆的周长公式,代入数值计算即可求出半径。
【详解】12.56÷3.14÷2
=4÷2
=2(厘米)
【点睛】解答本题的关键是理解用圆规画圆时,圆规两脚间的距离就是所画圆的半径。
12.12
【分析】先求出正方形的边长最小是多少厘米,即求4和3的最小公倍数;然后根据求出的正方形的边长进行分析:看能放几排,几列,然后相乘即可。
【详解】4×3=12
所以4和3的最小公倍数是12
(12÷4)×(12÷3)
=3×4
=12(块)
【点睛】解决本题先理解怎么样才能拼成一个正方形,然后找出这个正方形的边长,再求几个长(几个宽)才能拼成边长,进而求解。
13.
【分析】车轮转动一圈的距离即为车轮圆的周长,根据圆的周长=,得出两个车轮的周长,在运用比的基本性质化简得到答案。
【详解】由题意可得:爸爸的脚踏车转动一圈距离为:28π英寸,明明的脚踏车车轮转动一圈的距离为:20π英寸;故明明和爸爸脚踏车车轮分别转动一周前进距离的比为:。
【点睛】本题主要考查的是圆的周长及比的应用,解题的关键是熟练掌握比的化简方法,进而得出答案。
14.3∶4
【分析】由圆的周长公式可知,圆的周长与圆的半径有关,小圆与大圆的周长比等于小圆与大圆的半径比,据此解答。
【详解】假设大圆的半径为1,则小圆的半径为。
小圆的周长∶大圆的周长=∶1=3∶4
【点睛】两个圆的半径比等于直径比等于周长比,注意比的前项和后项是解答题目的关键。
15.157
【分析】从图中可知,长方形长的一半就是圆的半径,涂色部分的面积就是半圆的面积,据圆的面积公式,即可求出图中涂色部分的面积。
【详解】20÷2=10(厘米)
3.14×(10×10)÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
【点睛】理解图中长方形长的一半就是圆的半径,涂色部分的面积就是半圆的面积,这是解决此题的关键。
16.长方形
【分析】长方形特征:对边平行且相等,4个角都是直角的四边形,据此解答。
【详解】根据长方形的特征可知,小蜗牛后面藏的四边形可能是长方形。
【点睛】掌握长方形的特征是解答此题的关键。
17. 2 12.56
【分析】圆规两脚叉开的距离即为圆半径,根据圆的面积:S=πr2即可求出面积。
【详解】圆的半径为:2厘米;
圆的面积为:3.14×22
=3.14×4
=12.56(平方厘米)。
【点睛】此题考查了圆的面积,此题应明确:圆规两脚叉开的距离即为圆半径。
18.1500
【分析】先求出一组长和宽的和,长是5份,宽是3份,用长和宽的和÷(5+3),求出一份数,据此求出长和宽,再根据长方形的面积公式计算即可。
【详解】160÷2÷(5+3)
=80÷8
=10(米)
10×5=50(米)
10×3=30(米)
50×30=1500(平方米)
故答案为:1500
【点睛】本题考查了按比例分配应用题和长方形的周长及面积,长方形周长=(长+宽)×2,长方形面积=长×宽。
19.①见详解;9
②见详解;36
③见详解
【分析】①用数对表示位置,数对的第一个数表示列,第二个数表示行;在方格纸中描出A(1,1)、B(3,4)、C(7,1)三个点,依次连接成封闭图形;再根据三角形的面积=底×高÷2,求出这个三角形的面积。
②把三角形ABC的各边按2∶1的比放大,再根据三角形的面积公式求出放大后的三角形的面积。
③图形的放大与缩小的特点:形状相同,大小不同;据此解答。
【详解】①三角形ABC的底是6厘米,高是3厘米;
三角形ABC的面积是:
6×3÷2
=18÷2
=9(平方厘米)
②放大后的三角形的底是:6×2=12(厘米)
放大后的三角形的高是:3×2=6(厘米)
放大后三角形的面积是:
12×6÷2
=72÷2
=36(平方厘米)
如图:
③比较三角形ABC和放大后的三角形,大小发生了变化,形状没变。
【点睛】掌握根据数对找位置、三角形的面积的计算、作放大后的图形以及图形放大的特点是解题的关键。
20.(1)见详解(2)16
【分析】(1)观图可知:三角形的两条直角边是1和2,按4∶1的比画出扩大后的三角形的两条直角边分别是1×4=4(厘米),2×4=8(厘米),据此即可画图;
(2)根据三角形的面积S=ah÷2,代入数据解答即可。
【详解】(1)1×4=4(厘米)
2×4=8(厘米)
作图如下:
(2)4×8÷2
=32÷2
=16(平方厘米)
【点睛】此题考查了图形的放大与缩小及三角形面积公式的应用。
21.(1)是;因为最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等。
(2)
【分析】(1)根据∠A∶∠B∶∠C=1∶1∶2,可知最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等,所以这个三角形是等腰直角三角形。
(2)三角形的面积=底×高÷2,那么底×高=三角形的面积×2,根据(1)可知这个三角形是等腰直角三角形,那么底和高相等,进而求出腰长,据此画图。
【详解】略
22.(1)
(2)1∶3;4平方厘米
【分析】图形缩小的意义:图形按照一定比例变小,但形状没有发生变化。
【详解】原图形底为6 cm,高为12 cm。
按1∶3缩小,缩小后底为:(cm),高为:(cm)
缩小后面积为:2×4×=8×=4(cm2)
【点睛】选定的缩小的比的后项,得是原图形的底和高的公因数。这样原图形的底和高才能被比的后项整除,得到整数长的底和高。
23.14厘米
【分析】阴影(I)的面积比阴影(II)的面积大17平方厘米,也就是半圆的面积比三角形ABC的面积大17平方厘米,据此可知本题的数量的关系:半圆面积﹣三角形ABC面积=17,据此数量关系可列方程解答。
【详解】解:设BC长x厘米,根据题意得:
3.14×(20÷2)2÷2﹣20x÷2=17
3.14×100÷2﹣10x=17
157﹣10x=17
157﹣17=10x
10x=140
x=14
答:BC的长度是14厘米。
【点睛】本题的关键是根据半圆的面积比三角形ABC的面积大17平方厘米,找出数量关系,再列方程解答。
试卷第1页,共3页
试卷第1页,共3页
同课章节目录
