6.1平面向量的概念 课件(共17张PPT)
文档属性
| 名称 | 6.1平面向量的概念 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 496.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-16 19:44:00 | ||
图片预览





文档简介
(共17张PPT)
平面向量的概念
五一期间,小张同学发来消息说她考上了省内地级市的高职院校,离象山县直线距离210公里,让老师猜她在哪个地级市?
一、情景引入
不仅考虑大小,还要考虑方向.
A
B
问题1:你能否再举出既有大小,又有方向的量?
重力、电场强度、速度、加速度等等
追问:有没有只有大小的量?
身高、体重、年龄、面积、体积等等
一、情景引入
1、定义
在数学中,我们把这种既有大小又有方向的量叫做向量.
只有大小的量叫做数量.
例1 下列哪些量是向量?(p4)
拉力、压强、摩擦力、频率、加速度
二、构建概念
1、定义
在数学中,我们把这种既有大小又有方向的量叫做向量.
只有大小的量叫做数量.
二、构建概念
数量:定义
——表示法
——特殊的数量
——关系
——运算
向量:定义
——表示法
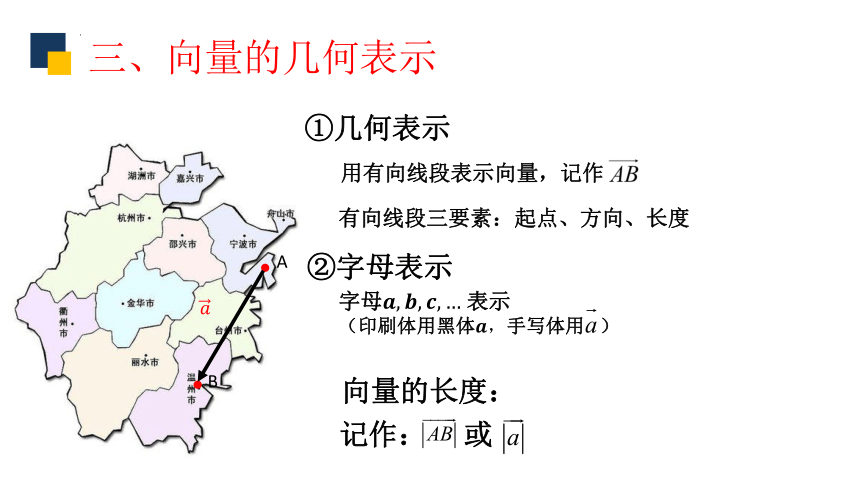
三、向量的几何表示
①几何表示
用有向线段表示向量,记作
记作: 或
向量的长度:
②字母表示
字母 表示
(印刷体用黑体手写体用 )
有向线段三要素:起点、方向、长度
A
B
思考:“向量就是有向线段,有向线段就是向量”,这种说法对吗?
三、向量的几何表示
有向线段三要素:起点、方向、长度
①零向量:长度为0的向量叫做零向量,记作
②单位向量:长度等于1 个单位的向量,叫做单位向量
四、特殊向量
.
方向任意
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
(1)图中哪些向量是单位向量?
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
(2)向量的方向有何关系?
方向相同
相反
方向相反
平行向量:方向相同或相反的非零向量.
记作: 或者
规定:零向量与任意向量平行,即对任意向量,
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
相等向量:长度相等且方向相同的向量
记作:或者
(3)在大小和方向上有何关系?
大小相等,方向相同
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
思考:能否将图中所有的向量都平移到同一条直线上?
任一组平行向量都可以平移到同一条直线上,所以平行向量也叫做共线向量.
平行向量
共线向量
1、判断下列结论与否正确,并说明理由.
(1)若与都是单位向量,则
(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.
(3)直角坐标平面上的轴、轴都是向量.
(4)若与是平行向量,则
(5)若用有向线段表示的向量与不相等,则M和N不重合.
(6)海拔、温度、角度都不是向量.
六、巩固应用
×
×
×
√
√
√
2、如图,设O是正六边形ABCDEF的中心.
(1)写出图中的共线向量;
是共线向量;
是共线向量;
是共线向量.
六、巩固应用
A
B
C
D
E
F
O
2、如图,设O是正六边形ABCDEF的中心.
(2)分别写出与的向量.
;
;
六、巩固应用
A
B
C
D
E
F
O
向量
向量定义:大小、方向
特殊关系
平行向量(共线向量)
相等向量
几何表示
七、课堂小结
向量表示
特殊向量
符号表示
模:
零向量
单位向量
作业:课后习题
谢谢聆听!
平面向量的概念
五一期间,小张同学发来消息说她考上了省内地级市的高职院校,离象山县直线距离210公里,让老师猜她在哪个地级市?
一、情景引入
不仅考虑大小,还要考虑方向.
A
B
问题1:你能否再举出既有大小,又有方向的量?
重力、电场强度、速度、加速度等等
追问:有没有只有大小的量?
身高、体重、年龄、面积、体积等等
一、情景引入
1、定义
在数学中,我们把这种既有大小又有方向的量叫做向量.
只有大小的量叫做数量.
例1 下列哪些量是向量?(p4)
拉力、压强、摩擦力、频率、加速度
二、构建概念
1、定义
在数学中,我们把这种既有大小又有方向的量叫做向量.
只有大小的量叫做数量.
二、构建概念
数量:定义
——表示法
——特殊的数量
——关系
——运算
向量:定义
——表示法
三、向量的几何表示
①几何表示
用有向线段表示向量,记作
记作: 或
向量的长度:
②字母表示
字母 表示
(印刷体用黑体手写体用 )
有向线段三要素:起点、方向、长度
A
B
思考:“向量就是有向线段,有向线段就是向量”,这种说法对吗?
三、向量的几何表示
有向线段三要素:起点、方向、长度
①零向量:长度为0的向量叫做零向量,记作
②单位向量:长度等于1 个单位的向量,叫做单位向量
四、特殊向量
.
方向任意
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
(1)图中哪些向量是单位向量?
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
(2)向量的方向有何关系?
方向相同
相反
方向相反
平行向量:方向相同或相反的非零向量.
记作: 或者
规定:零向量与任意向量平行,即对任意向量,
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
相等向量:长度相等且方向相同的向量
记作:或者
(3)在大小和方向上有何关系?
大小相等,方向相同
五、向量之间的关系
注:每个小正方形网格边长为1 的单位长度
1
A
B
C
D
E
F
G
H
J
K
思考:能否将图中所有的向量都平移到同一条直线上?
任一组平行向量都可以平移到同一条直线上,所以平行向量也叫做共线向量.
平行向量
共线向量
1、判断下列结论与否正确,并说明理由.
(1)若与都是单位向量,则
(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.
(3)直角坐标平面上的轴、轴都是向量.
(4)若与是平行向量,则
(5)若用有向线段表示的向量与不相等,则M和N不重合.
(6)海拔、温度、角度都不是向量.
六、巩固应用
×
×
×
√
√
√
2、如图,设O是正六边形ABCDEF的中心.
(1)写出图中的共线向量;
是共线向量;
是共线向量;
是共线向量.
六、巩固应用
A
B
C
D
E
F
O
2、如图,设O是正六边形ABCDEF的中心.
(2)分别写出与的向量.
;
;
六、巩固应用
A
B
C
D
E
F
O
向量
向量定义:大小、方向
特殊关系
平行向量(共线向量)
相等向量
几何表示
七、课堂小结
向量表示
特殊向量
符号表示
模:
零向量
单位向量
作业:课后习题
谢谢聆听!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
