浙教版初中数学模拟试卷2023年05月衢州适用(含解析)
文档属性
| 名称 | 浙教版初中数学模拟试卷2023年05月衢州适用(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 00:00:00 | ||
图片预览


文档简介
浙教版初中数学模拟试卷2023年05月衢州适用
一、选择题(本题共有10小题,每小题3分,共30分)
1.下列图形中,是中心对称的有( )
A.1个 B.2个 C.3个 D.4个
2.-3的绝对值是()
A.3 B.-3 C. D.
3.如果 ,那么点P 所在象限为( )
A.第二象限 B.第四象限
C.第一或第三象限 D.第二或第四象限
4.甲、乙两图分别表示2018年和2019年郑州市财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )
A.2018年教育经费占财政经费支出比例较高
B.2018年教育经费支出金额比较多
C.2018年教育经费支出增幅比较大
D.2018年财政经费支出总额比较小
5.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+k+2=0的两根,则k的值为( )
A.30 B.34或30 C.36或30 D.34
6.某校体育器材室有篮球和足球共66个,其中篮球比足球的2倍多3个,设篮球有x个,足球有y个,根据题意可得方程组( )
A. B.
C. D.
7.若关于x的一元一次不等式组 的解集是x a,且关于y的分式方程 有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
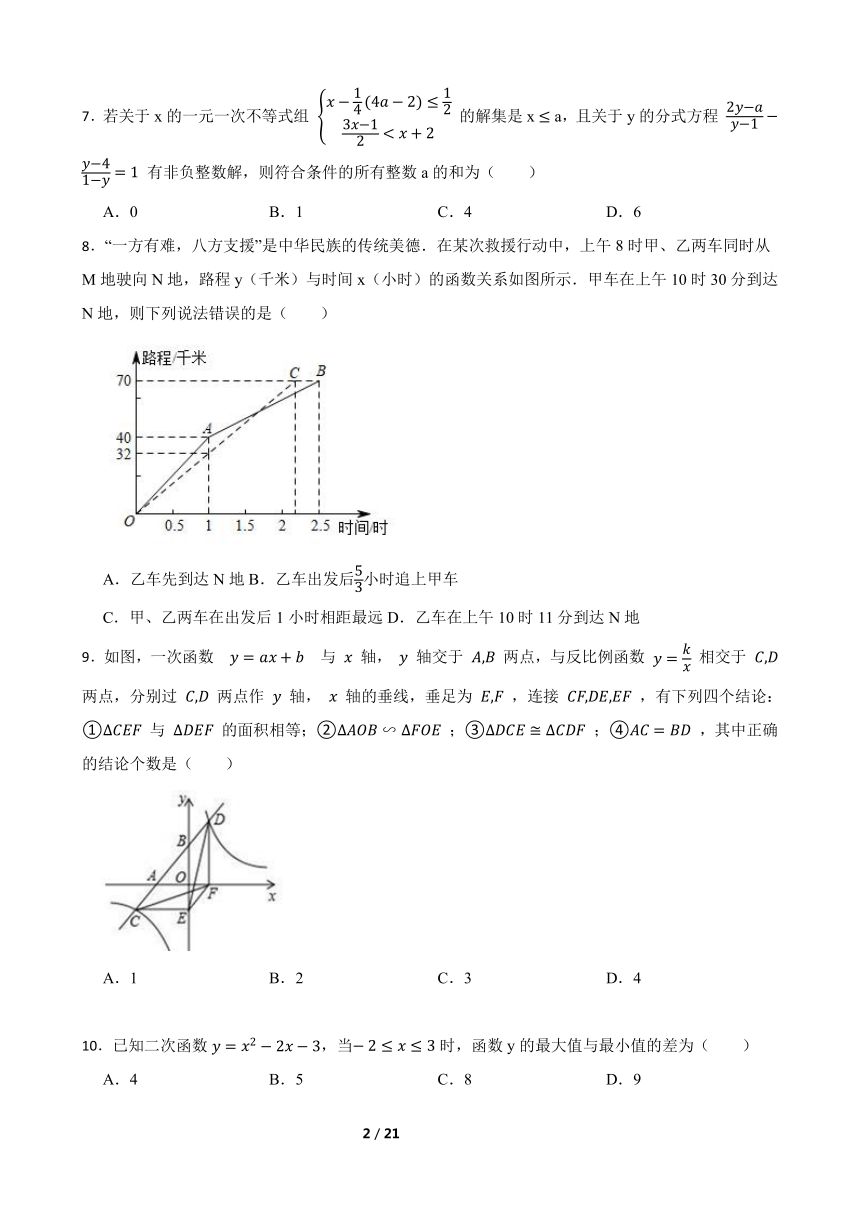
8.“一方有难,八方支援”是中华民族的传统美德.在某次救援行动中,上午8时甲、乙两车同时从M地驶向N地,路程y(千米)与时间x(小时)的函数关系如图所示.甲车在上午10时30分到达N地,则下列说法错误的是( )
A.乙车先到达N地B.乙车出发后小时追上甲车
C.甲、乙两车在出发后1小时相距最远D.乙车在上午10时11分到达N地
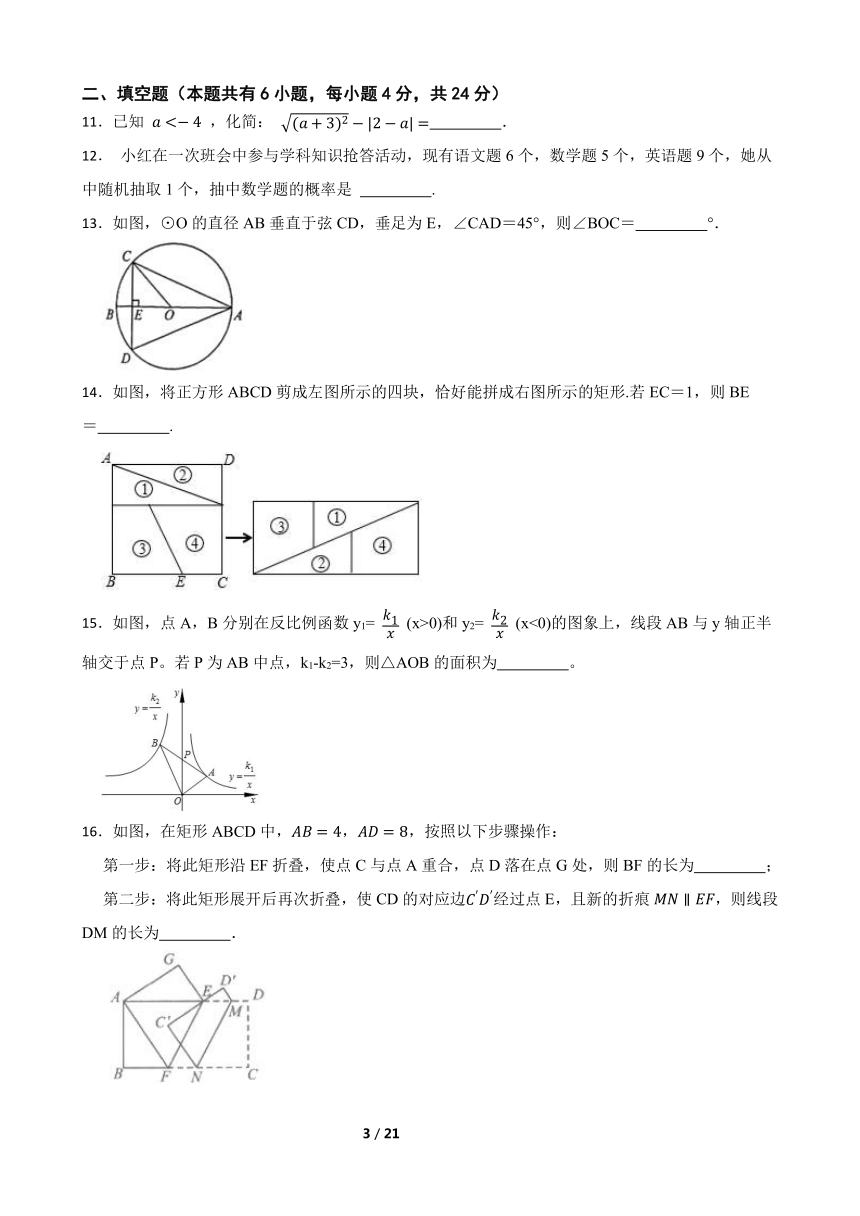
9.如图,一次函数 与 轴, 轴交于 两点,与反比例函数 相交于 两点,分别过 两点作 轴, 轴的垂线,垂足为 ,连接 ,有下列四个结论:① 与 的面积相等;② ∽ ;③ ;④ ,其中正确的结论个数是( )
A.1 B.2 C.3 D.4
10.已知二次函数,当时,函数y的最大值与最小值的差为( )
A.4 B.5 C.8 D.9
二、填空题(本题共有6小题,每小题4分,共24分)
11.已知 ,化简: .
12. 小红在一次班会中参与学科知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是 .
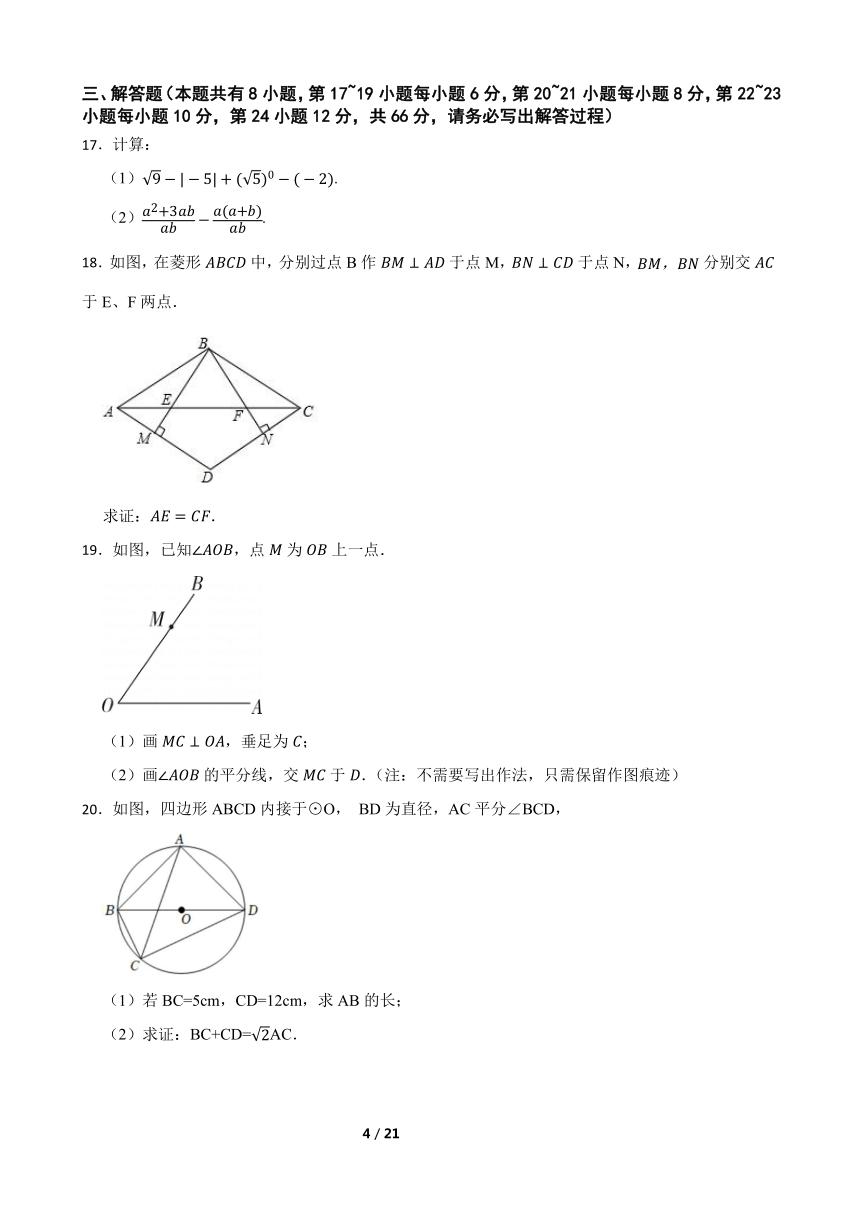
13.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠CAD=45°,则∠BOC= °.
14.如图,将正方形ABCD剪成左图所示的四块,恰好能拼成右图所示的矩形.若EC=1,则BE= .
15.如图,点A,B分别在反比例函数y1= (x>0)和y2= (x<0)的图象上,线段AB与y轴正半轴交于点P。若P为AB中点,k1-k2=3,则△AOB的面积为 。
16.如图,在矩形ABCD中,,,按照以下步骤操作:
第一步:将此矩形沿EF折叠,使点C与点A重合,点D落在点G处,则BF的长为 ;
第二步:将此矩形展开后再次折叠,使CD的对应边经过点E,且新的折痕,则线段DM的长为 .
三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分,请务必写出解答过程)
17.计算:
(1).
(2).
18.如图,在菱形中,分别过点B作于点M,于点N,分别交于E、F两点.
求证:.
19.如图,已知,点为上一点.
(1)画,垂足为;
(2)画的平分线,交于.(注:不需要写出作法,只需保留作图痕迹)
20.如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,
(1)若BC=5cm,CD=12cm,求AB的长;
(2)求证:BC+CD=AC.
21.今年3月5日是第58个“学习雷锋纪念日”,某校组织七、八年级全体学生开展“学习雷锋知识竞赛活动”.为了解竞赛成绩情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级80,80,85,85,90,90,90,95,95,100;八年级80,85,85,90,90,90,90,95,95,100.分析数据如表:
平均数 中位数 众数 方差
七年级 a 90 90 39
八年级 90 90 b 30
根据以上信息回答下列问题:
(1)求出表格中a,b的值;
(2)通过数据分析,你认为哪个年级的成绩比较好?请说明理由.
22.我市某公司分两次采购了一批原料,已知第二次的采购数量是第一次采购数量的两倍,其它信息如下表:
第一次 第二次
每吨原料的价格(元) m+500 m-500
采购费用(万元) 40 60
(1)求m的值,并求出这两次共采购了多少吨原料?
(2)该公司可将原料加工成A型产品或B型产品,而受设备限制每天只能安排加工一种型号产品.经统计,加工A型产品与B型产品各1天共需用原料数为20吨,加工3天A型产品与加工2天B型产品所需用原料数相等.请求出加工成A,B型产品每天所需的原料数分别是多少吨?
(3)该公司将生产的两种产品全部出口国外,每吨原料加工成A,B型产品后的获利分别是1000元与600元,但要求加工时间不超过30天.为了使总利润获得最大,应采用怎样的加工方案?
23.跳台滑雪是北京冬奥会的比赛项目之一.下图是某跳台滑雪场地的截面示意图. 平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米.经实验表明:h=6t2,l=vt.
(1)求k的值;
(2)当v=5,t=1时,通过计算判断运动员是否落在滑道上;
(3)若运动员甲、乙同时从A处飞出,已知甲离开点A的速度是5米/秒.当甲距x轴4.5米时,乙恰好位于甲右侧4.5米的位置,求t的值与运动员乙离开A的速度.
24.如图,在 中, ,点 是 上一动点 ,以点 为圆心, 长为半径作 交线段 于点 ,连结 并延长交 于点 .
(1)求 的长.
(2)当 为何值时, 是等腰三角形?
(3)求 取到最大值时 的长.
答案解析部分
1.【答案】B
【解析】【解答】解:从左到右,第一、第二、第三个图形是中心对称图形,第四个图形不是中心对称图形.
故中心对称图形有3个.
故答案为:B.
【分析】根据中心对称图形的定义逐项判断即可。
2.【答案】A
【解析】【分析】计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号.
【解答】-3的绝对值是3.故选:A
【点评】规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
3.【答案】D
【解析】【解答】解:∵ab<0,
∴①a<0时,b>0,
此时点P(a,b)在第二象限,
②a>0时,b<0,
此时,点P(a,b)在第四象限,
所以,点P(a,b)在第二或第四象限.
故答案为:D.
【分析】根据有理数乘法同号得正,异号得负确定出a、b是异号两数,再根据各象限内点的特点解答.
4.【答案】A
【解析】【解答】解:通过2个扇形图比较,2018年教育支出的扇形面积大于2019年教育支出的扇形面积
故2018年教育支出占财经支出的比例比2019年高
而我们不知2018、2019年的具体总支出,其它信息不可得出
故答案为:A.
【分析】 因为2018年和2019年财政经费支出的总数额未知,教育经费支出增幅也看不出来,通过扇形统计图只能看出教育经费占财政经费支出比率可以比较,由此可知2018年教育经费占财政经费支出比率较高.
5.【答案】D
【解析】【解答】解:当 时, 时,
是关于x的一元二次方程 的两根,
,
不符合;
当 时, ,
是关于x的一元二次方程 的两根,
,
不符合;
当 时,
是关于x的一元二次方程 的两根,
,
,
,
;
故答案为:D.
【分析】当a=4时,根据三角形的三边关系确定出b的范围,根据根与系数的关系可得4+b=12,求出b的值,然后进行验证;当b=4时,根据三角形的三边关系确定出a的范围,根据根与系数的关系可得4+a=12,求出a的值,然后进行验证;当a=b时,根据根与系数的关系可得12=2a=2b,求出a、b的值,然后根据ab=k+2就可得到k的值.
6.【答案】B
【解析】【解答】解:设篮球有x个,足球有y个,
依题意,得: .
故答案为:B.
【分析】设篮球有x个,足球有y个,根据题意可得:篮球的个数+足球的个数=66,篮球的个数=足球个数的2倍+3,分别代入未知数建立二元一次方程组,据此选择即得.
7.【答案】B
【解析】【解答】解:由不等式组 ,解得:
∵解集是x≤a,
∴a<5;
由关于y的分式方程 得2y-a+y-4=y-1
又∵该方程有非负整数解,
∴a≥-3,
∴a=-3,a=-1(舍,此时分式方程为增根),a=1,a=3,
∴符合条件的所有整数a的和为 1.
故答案为:B.
【分析】先解关于x的一元一次不等式组 ,再根据其解集是x≤a,得a小于5;再解分式方程,根据其有非负整数解,同时考虑增根的情况,得出a的值,再求和即可.
8.【答案】D
【解析】【解答】A.根据图像可得,乙车的速度是32÷1=32(千米/小时),
故乙车到达N地需要:70÷32==2.1875(小时),
∵2.5>2.1875,
∴乙车先到达N地,不符合题意;
B.甲车在第1个小时行驶了40km,在AB段的速度是:(千米/小时),
可设乙车出发t小时后追上甲车,
则有:40+20(t-1)=32t,
解得:,不符合题意;
C.根据图像可得甲、乙两车在出发后1小时相距40-32=8(千米),
当乙车到达N地时,两车相距:(千米),
∵8>6.25,
∴甲、乙两车在出发后1小时相距最远,不符合题意;
D.根据题意得:乙车到达N地需要:70÷32=(小时),
8+小时=10时11.25分,
故乙车在上午10时11.25分到达N地,符合题意;
故答案为:D
【分析】根据函数图象中数据,再结合速度、时间和路程的关系求解即可。
9.【答案】C
【解析】【解答】解:①设D(x, ),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是 × ×x= k,
同理可知:△CEF的面积是 k,
∴△CEF的面积等于△DEF的面积,∴①正确;②即△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
∴EF∥CD,
即AB∥EF,
∴△AOB∽△FOE,∴②正确;③条件不足,无法证出两三角形全等的条件,∴③错误;④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,∴④正确;
正确的有3个,
故答案为:C.
【分析】设D(x, ),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据面积相等,推出边EF上的高相等,推出CD∥EF,根据相似三角形的判定判断②即可;根据全等三角形的判定判断③即可;证出平行四边形BDFE和平行四边形ACEF,推出△ACF和△BDE的面积相等,根据三角形的面积公式推出BD=AC即可.
10.【答案】D
【解析】【解答】解:,如图,
∴二次函数的开口向上,对称轴为,
∴当时,函数有最小值,
当时,,当时,
∴当时,有最大值
,
故答案为:D.
【分析】由于二次函数的开口向上,对称轴为,在内,当x=-2时y为最大值,当x=1时y为最小值,分别求值再相减即可.
11.【答案】-5
【解析】【解答】∵ ,
∴a+3<0,2-a>0,
∴ -a-3-2+a=-5,
故答案为:-5.
【分析】利用二次根式及绝对值的性质化简,再合并同类项即可。
12.【答案】
【解析】【解答】解:P(抽到数学)= 。
故答案为: 。
【分析】由抽到数学题的概率=数学题的数量÷所有题目的数量即可算出答案。
13.【答案】45
【解析】【解答】解:∵⊙O的直径AB垂直于弦CD,
∴CE=DE,
∴ AB垂直平分CD
∴AC=AD
∴△ACD是等腰三角形
∴∠BAC=∠CAD=×45°=22.5°
∴∠BOC=2∠BAC=45°,
故答案为:45.
【分析】先证明△ACD是等腰三角形,再利用等腰三角形的性质可得∠BAC=∠CAD=×45°=22.5°,最后利用圆周角的性质可得∠BOC=2∠BAC=45°。
14.【答案】
【解析】【解答】设BE=b,EC=a,依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b= ,而b不能为负,
∴BE=b= ,
故答案为: .
【分析】设BE=b,EC=a,由图知:正方形的边长为(a+b);长方形的长为(a+a+b),宽为b;所以根据正方形的面积等于长方形的面积可得等式:(a+b)2=b(b+a+b);把EC=a=1代入等式可得关于b的方程,解方程即可求解。
15.【答案】
【解析】【解答】解:设A(a,b),B(m,n),
∴P(),
∴ ,
∴a=-m,
∵ab=k1, mn=k2,
∵△AOB的面积=(xA×OP+xB×OP),
=(xA+xB)×OP
=(a-m)×
=×2a×
=
=
=
=.
故答案为:.
【分析】设A(a,b),B(m,n), 用中点坐标公式把P点坐标表示出来,得出a=-m, 再用三角形面积公式求出 △AOB的面积表达式,结合反比例函数的坐标特点,把面积转化为用含k1、k2的代数式表示,代入 k1-k2=3即可求出其面积.
16.【答案】3;
【解析】【解答】解:第一步:由题意得:,
,
∴在Rt△ABF中,
即,
解得;
第二步:由折叠的性质可知,,,
,
,,
,
,
又
,
由第一步知,,,
,
设,则,
∵,
∴,
解得,
∴.
故答案为:3,.
【分析】第一步:根据折叠的性质可得,,在Rt△ABF中,根据勾股定理可得即,解得;第二步:由折叠的性质可知,,
证明,,由第一步知,,,,设,则,,,解得,则.
17.【答案】(1)解:原式
;
(2)解:原式
.
【解析】【分析】(1)此题的运算顺序:先算乘方和开方运算,再利用有理数的加减法法则进行计算.
(2)利用同分母分式相减的法则:分母不变,把分子相减,再约分即可.
18.【答案】证明:∵四边形是菱形,
∴,
∴,
又∵,
∴,
∴.
在和中,
,
∴,
∴.
【解析】【分析】根据菱形的性质可得AB=BC,∠BAE=∠DAE=∠DCA=∠BCF,由垂直的概念可得∠AMB=∠CNB=90°,根据同角的余角相等可得∠ABE=∠CBF,证明△ABE≌△CBF,据此可得结论.
19.【答案】(1)解:如图,为所作;
(2)解:如图,为所作;
【解析】【分析】根据要求作出图象即可。
20.【答案】(1)解:∵BD为直径,
∴∠BAD=∠BCD=90°,
∵CD=12cm,BC=5cm,
∴BD=13(cm),
∵AC平分∠BCD,
∴∠ABD=∠ADB=45°,
∴AB=AD,
∴AB=AD=BD=,故AB的长为
(2)证明:将△ACD绕点A顺时针旋转90°后可得△ABC′,
由旋转性质可得:△ACD△ABC′,∠CAC′=90°,CA=C′A,
∴AC′=AC,CD=BC′,∠ADC=ABC′,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC+∠AD′B=180°,
又∵∠CAC′=90°,CA=C′A,
∴△C′AC是等腰直角三角形,
∴CC′=,
∴BC+C′B=,
∴BC+CD=.
【解析】【分析】(1)因为AC平分,同一个圆内圆周角度数相同对应的弦长也相同,所以AB=AD,为等腰直角三角形,根据已知条件,利用勾股定理就可以求出AB
(2)顺时针旋转90°,根据旋转的性质得到 ∠CAC′=90°,CA=C′A , CD=BC′,∠ADC=ABC ,再证明C'在CB的延长线上,于是判断为等腰直角,从而证明。
21.【答案】(1)解:a= ×(80×2+85×2+90×3+95×3+100)=89,b=90
(2)解:七,八年级学生成绩的中位数与众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更整齐,
∴八年级学生成绩较好.
【解析】【分析】(1)根据平均数和众数的定义求解即可;(2)从平均数、中位数及方差的意义求解即可.
22.【答案】(1)解:根据题意得: ,
解得:m=3500,经检验是原方程的根且符合题意;
共采购原料= 吨
(2)解:设加工成A,B型产品每天所需的原料数分别是x,y吨,
则 ,解得: ;
答:加工成A,B型产品每天所需的原料数分别是8吨、12吨。
(3)解:设加工成A型产品的原料数为a吨,总利润为y元,
则: ,解得:a≤120;
又y=1000a+600(300-a)=400a+180000
∵y随着a的增大而增大,∴当a=120时,获得最大利润;
∴原料120吨加工成A型产品,原料180吨加工成B型产品
【解析】【分析】(1)根据总价除以单价等于数量得出,第一次采购的数量为吨,第二次采购的数量为吨,根据 第二次的采购数量是第一次采购数量的两倍列出方程,求解并检验即可;
(2) 设加工成A,B型产品每天所需的原料数分别是x,y吨 ,根据 加工A型产品与B型产品各1天共需用原料数为20吨 及 加工3天A型产品与加工2天B型产品所需用原料数相等 列出方程,求解即可;
(3) 设加工成A型产品的原料数为a吨,总利润为y元, 则a吨原材料加工成A产品的时间为天,(300-a)吨原材料加工成B产品的时间为天,根据加工A产品的时间+加工B产品的时间 不超过30天 列出不等式,求解即可得出a的取值范围;根据销售A产品的利润+销售B产品的利润等于总利润建立出y与a的函数关系式,根据所得函数的性质即可解决问题。
23.【答案】(1)解:由题意:A(1,18),
把A(1,18)代入得18=,
解得k=18;
(2)解:当v=5,t=1时,h=6t2=6,l=vt=5,
xM=1+5=6,yM=18-6=12,即M(6,12),
把x=6代入得y=3≠12,
∴运动员不在滑道上
(3)解:由题意知h甲=18-4.5=6t2,
解得:t=1.5;
∵,
∴1.5(v乙-5)=4.5,解得v乙=8
答:t的值为1.5,运动员乙离开A的速度为8米/秒.
【解析】【分析】(1)把A(1,18)代入中,求出k值;
(2)先求出M坐标,再将其代入 中检验即可;
(3) 由题意知h甲=18-4.5=6t2,解得t=1.5,根据建立方程,求解即可.
24.【答案】(1)解: ,
.
(2)解: ,
,
①当 时,如图1,
,
,
.
②当 时,如图2.
过 作 ,
∵AD=BD,∠BAO=90°,
∴BF=AF,DF∥OA,
为 的中点,
,
,
.
③当 时,如图3.
过 作 ,
设 ,则 ,
由勾股定理得 ,
解得 或 .
(舍去)或 ,
.
综上所述, 或 或 .
(3)解:分别过点 作 的垂线段,垂足为 ,如图4.
,
,
,
,
,
,
即 ,
, .
设半径为 ,
,
.
又 ,在 范围内,
∴当 时, 取得最大值,此时, .
取到最大值时 的长为 .
【解析】【分析】(1)在Rt△BAO中利用余弦三角函数即可求出AB的长;
(2)首先利用勾股定理求出OA的长,然后分三种情况讨论,即 ①当 时, 先求出OD的长,则半径OC长可求,然后根据线段的和差关系即可求出AC的长; ②当 时,过作 , 根据三角形的中位线定理求出OD的长,则AC长可求; ③当 时,过 作 , 设,在Rt△DGO中利用勾股定理列式求出OD长,则AC长可求;
(3) 分别过点 作 的垂线段,垂足为 , 先证明△AMD∽△OND,利用相似三角形的性质得出AD·DN=DM·OD,设圆的半径为r,用圆的半径表示出AD和DE的乘积,构造二次函数求解即可.
1 / 1
一、选择题(本题共有10小题,每小题3分,共30分)
1.下列图形中,是中心对称的有( )
A.1个 B.2个 C.3个 D.4个
2.-3的绝对值是()
A.3 B.-3 C. D.
3.如果 ,那么点P 所在象限为( )
A.第二象限 B.第四象限
C.第一或第三象限 D.第二或第四象限
4.甲、乙两图分别表示2018年和2019年郑州市财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )
A.2018年教育经费占财政经费支出比例较高
B.2018年教育经费支出金额比较多
C.2018年教育经费支出增幅比较大
D.2018年财政经费支出总额比较小
5.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2﹣12x+k+2=0的两根,则k的值为( )
A.30 B.34或30 C.36或30 D.34
6.某校体育器材室有篮球和足球共66个,其中篮球比足球的2倍多3个,设篮球有x个,足球有y个,根据题意可得方程组( )
A. B.
C. D.
7.若关于x的一元一次不等式组 的解集是x a,且关于y的分式方程 有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
8.“一方有难,八方支援”是中华民族的传统美德.在某次救援行动中,上午8时甲、乙两车同时从M地驶向N地,路程y(千米)与时间x(小时)的函数关系如图所示.甲车在上午10时30分到达N地,则下列说法错误的是( )
A.乙车先到达N地B.乙车出发后小时追上甲车
C.甲、乙两车在出发后1小时相距最远D.乙车在上午10时11分到达N地
9.如图,一次函数 与 轴, 轴交于 两点,与反比例函数 相交于 两点,分别过 两点作 轴, 轴的垂线,垂足为 ,连接 ,有下列四个结论:① 与 的面积相等;② ∽ ;③ ;④ ,其中正确的结论个数是( )
A.1 B.2 C.3 D.4
10.已知二次函数,当时,函数y的最大值与最小值的差为( )
A.4 B.5 C.8 D.9
二、填空题(本题共有6小题,每小题4分,共24分)
11.已知 ,化简: .
12. 小红在一次班会中参与学科知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是 .
13.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠CAD=45°,则∠BOC= °.
14.如图,将正方形ABCD剪成左图所示的四块,恰好能拼成右图所示的矩形.若EC=1,则BE= .
15.如图,点A,B分别在反比例函数y1= (x>0)和y2= (x<0)的图象上,线段AB与y轴正半轴交于点P。若P为AB中点,k1-k2=3,则△AOB的面积为 。
16.如图,在矩形ABCD中,,,按照以下步骤操作:
第一步:将此矩形沿EF折叠,使点C与点A重合,点D落在点G处,则BF的长为 ;
第二步:将此矩形展开后再次折叠,使CD的对应边经过点E,且新的折痕,则线段DM的长为 .
三、解答题(本题共有8小题,第17~19小题每小题6分,第20~21小题每小题8分,第22~23小题每小题10分,第24小题12分,共66分,请务必写出解答过程)
17.计算:
(1).
(2).
18.如图,在菱形中,分别过点B作于点M,于点N,分别交于E、F两点.
求证:.
19.如图,已知,点为上一点.
(1)画,垂足为;
(2)画的平分线,交于.(注:不需要写出作法,只需保留作图痕迹)
20.如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,
(1)若BC=5cm,CD=12cm,求AB的长;
(2)求证:BC+CD=AC.
21.今年3月5日是第58个“学习雷锋纪念日”,某校组织七、八年级全体学生开展“学习雷锋知识竞赛活动”.为了解竞赛成绩情况,从两个年级各随机抽取了10名同学的成绩(满分为100分),收集数据为:七年级80,80,85,85,90,90,90,95,95,100;八年级80,85,85,90,90,90,90,95,95,100.分析数据如表:
平均数 中位数 众数 方差
七年级 a 90 90 39
八年级 90 90 b 30
根据以上信息回答下列问题:
(1)求出表格中a,b的值;
(2)通过数据分析,你认为哪个年级的成绩比较好?请说明理由.
22.我市某公司分两次采购了一批原料,已知第二次的采购数量是第一次采购数量的两倍,其它信息如下表:
第一次 第二次
每吨原料的价格(元) m+500 m-500
采购费用(万元) 40 60
(1)求m的值,并求出这两次共采购了多少吨原料?
(2)该公司可将原料加工成A型产品或B型产品,而受设备限制每天只能安排加工一种型号产品.经统计,加工A型产品与B型产品各1天共需用原料数为20吨,加工3天A型产品与加工2天B型产品所需用原料数相等.请求出加工成A,B型产品每天所需的原料数分别是多少吨?
(3)该公司将生产的两种产品全部出口国外,每吨原料加工成A,B型产品后的获利分别是1000元与600元,但要求加工时间不超过30天.为了使总利润获得最大,应采用怎样的加工方案?
23.跳台滑雪是北京冬奥会的比赛项目之一.下图是某跳台滑雪场地的截面示意图. 平台AB长1米(即AB=1),平台AB距地面18米.以地面所在直线为x轴,过点B垂直于地面的直线为y轴,取1米为单位长度,建立平面直角坐标系.已知滑道对应的函数为.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落过程中的某位置(忽略空气阻力).设运动员飞出时间为t秒,运动员与点A的竖直距离为h米,运动员与点A的水平距离为l米.经实验表明:h=6t2,l=vt.
(1)求k的值;
(2)当v=5,t=1时,通过计算判断运动员是否落在滑道上;
(3)若运动员甲、乙同时从A处飞出,已知甲离开点A的速度是5米/秒.当甲距x轴4.5米时,乙恰好位于甲右侧4.5米的位置,求t的值与运动员乙离开A的速度.
24.如图,在 中, ,点 是 上一动点 ,以点 为圆心, 长为半径作 交线段 于点 ,连结 并延长交 于点 .
(1)求 的长.
(2)当 为何值时, 是等腰三角形?
(3)求 取到最大值时 的长.
答案解析部分
1.【答案】B
【解析】【解答】解:从左到右,第一、第二、第三个图形是中心对称图形,第四个图形不是中心对称图形.
故中心对称图形有3个.
故答案为:B.
【分析】根据中心对称图形的定义逐项判断即可。
2.【答案】A
【解析】【分析】计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号.
【解答】-3的绝对值是3.故选:A
【点评】规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
3.【答案】D
【解析】【解答】解:∵ab<0,
∴①a<0时,b>0,
此时点P(a,b)在第二象限,
②a>0时,b<0,
此时,点P(a,b)在第四象限,
所以,点P(a,b)在第二或第四象限.
故答案为:D.
【分析】根据有理数乘法同号得正,异号得负确定出a、b是异号两数,再根据各象限内点的特点解答.
4.【答案】A
【解析】【解答】解:通过2个扇形图比较,2018年教育支出的扇形面积大于2019年教育支出的扇形面积
故2018年教育支出占财经支出的比例比2019年高
而我们不知2018、2019年的具体总支出,其它信息不可得出
故答案为:A.
【分析】 因为2018年和2019年财政经费支出的总数额未知,教育经费支出增幅也看不出来,通过扇形统计图只能看出教育经费占财政经费支出比率可以比较,由此可知2018年教育经费占财政经费支出比率较高.
5.【答案】D
【解析】【解答】解:当 时, 时,
是关于x的一元二次方程 的两根,
,
不符合;
当 时, ,
是关于x的一元二次方程 的两根,
,
不符合;
当 时,
是关于x的一元二次方程 的两根,
,
,
,
;
故答案为:D.
【分析】当a=4时,根据三角形的三边关系确定出b的范围,根据根与系数的关系可得4+b=12,求出b的值,然后进行验证;当b=4时,根据三角形的三边关系确定出a的范围,根据根与系数的关系可得4+a=12,求出a的值,然后进行验证;当a=b时,根据根与系数的关系可得12=2a=2b,求出a、b的值,然后根据ab=k+2就可得到k的值.
6.【答案】B
【解析】【解答】解:设篮球有x个,足球有y个,
依题意,得: .
故答案为:B.
【分析】设篮球有x个,足球有y个,根据题意可得:篮球的个数+足球的个数=66,篮球的个数=足球个数的2倍+3,分别代入未知数建立二元一次方程组,据此选择即得.
7.【答案】B
【解析】【解答】解:由不等式组 ,解得:
∵解集是x≤a,
∴a<5;
由关于y的分式方程 得2y-a+y-4=y-1
又∵该方程有非负整数解,
∴a≥-3,
∴a=-3,a=-1(舍,此时分式方程为增根),a=1,a=3,
∴符合条件的所有整数a的和为 1.
故答案为:B.
【分析】先解关于x的一元一次不等式组 ,再根据其解集是x≤a,得a小于5;再解分式方程,根据其有非负整数解,同时考虑增根的情况,得出a的值,再求和即可.
8.【答案】D
【解析】【解答】A.根据图像可得,乙车的速度是32÷1=32(千米/小时),
故乙车到达N地需要:70÷32==2.1875(小时),
∵2.5>2.1875,
∴乙车先到达N地,不符合题意;
B.甲车在第1个小时行驶了40km,在AB段的速度是:(千米/小时),
可设乙车出发t小时后追上甲车,
则有:40+20(t-1)=32t,
解得:,不符合题意;
C.根据图像可得甲、乙两车在出发后1小时相距40-32=8(千米),
当乙车到达N地时,两车相距:(千米),
∵8>6.25,
∴甲、乙两车在出发后1小时相距最远,不符合题意;
D.根据题意得:乙车到达N地需要:70÷32=(小时),
8+小时=10时11.25分,
故乙车在上午10时11.25分到达N地,符合题意;
故答案为:D
【分析】根据函数图象中数据,再结合速度、时间和路程的关系求解即可。
9.【答案】C
【解析】【解答】解:①设D(x, ),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是 × ×x= k,
同理可知:△CEF的面积是 k,
∴△CEF的面积等于△DEF的面积,∴①正确;②即△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
∴EF∥CD,
即AB∥EF,
∴△AOB∽△FOE,∴②正确;③条件不足,无法证出两三角形全等的条件,∴③错误;④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,∴④正确;
正确的有3个,
故答案为:C.
【分析】设D(x, ),得出F(x,0),根据三角形的面积求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据面积相等,推出边EF上的高相等,推出CD∥EF,根据相似三角形的判定判断②即可;根据全等三角形的判定判断③即可;证出平行四边形BDFE和平行四边形ACEF,推出△ACF和△BDE的面积相等,根据三角形的面积公式推出BD=AC即可.
10.【答案】D
【解析】【解答】解:,如图,
∴二次函数的开口向上,对称轴为,
∴当时,函数有最小值,
当时,,当时,
∴当时,有最大值
,
故答案为:D.
【分析】由于二次函数的开口向上,对称轴为,在内,当x=-2时y为最大值,当x=1时y为最小值,分别求值再相减即可.
11.【答案】-5
【解析】【解答】∵ ,
∴a+3<0,2-a>0,
∴ -a-3-2+a=-5,
故答案为:-5.
【分析】利用二次根式及绝对值的性质化简,再合并同类项即可。
12.【答案】
【解析】【解答】解:P(抽到数学)= 。
故答案为: 。
【分析】由抽到数学题的概率=数学题的数量÷所有题目的数量即可算出答案。
13.【答案】45
【解析】【解答】解:∵⊙O的直径AB垂直于弦CD,
∴CE=DE,
∴ AB垂直平分CD
∴AC=AD
∴△ACD是等腰三角形
∴∠BAC=∠CAD=×45°=22.5°
∴∠BOC=2∠BAC=45°,
故答案为:45.
【分析】先证明△ACD是等腰三角形,再利用等腰三角形的性质可得∠BAC=∠CAD=×45°=22.5°,最后利用圆周角的性质可得∠BOC=2∠BAC=45°。
14.【答案】
【解析】【解答】设BE=b,EC=a,依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b= ,而b不能为负,
∴BE=b= ,
故答案为: .
【分析】设BE=b,EC=a,由图知:正方形的边长为(a+b);长方形的长为(a+a+b),宽为b;所以根据正方形的面积等于长方形的面积可得等式:(a+b)2=b(b+a+b);把EC=a=1代入等式可得关于b的方程,解方程即可求解。
15.【答案】
【解析】【解答】解:设A(a,b),B(m,n),
∴P(),
∴ ,
∴a=-m,
∵ab=k1, mn=k2,
∵△AOB的面积=(xA×OP+xB×OP),
=(xA+xB)×OP
=(a-m)×
=×2a×
=
=
=
=.
故答案为:.
【分析】设A(a,b),B(m,n), 用中点坐标公式把P点坐标表示出来,得出a=-m, 再用三角形面积公式求出 △AOB的面积表达式,结合反比例函数的坐标特点,把面积转化为用含k1、k2的代数式表示,代入 k1-k2=3即可求出其面积.
16.【答案】3;
【解析】【解答】解:第一步:由题意得:,
,
∴在Rt△ABF中,
即,
解得;
第二步:由折叠的性质可知,,,
,
,,
,
,
又
,
由第一步知,,,
,
设,则,
∵,
∴,
解得,
∴.
故答案为:3,.
【分析】第一步:根据折叠的性质可得,,在Rt△ABF中,根据勾股定理可得即,解得;第二步:由折叠的性质可知,,
证明,,由第一步知,,,,设,则,,,解得,则.
17.【答案】(1)解:原式
;
(2)解:原式
.
【解析】【分析】(1)此题的运算顺序:先算乘方和开方运算,再利用有理数的加减法法则进行计算.
(2)利用同分母分式相减的法则:分母不变,把分子相减,再约分即可.
18.【答案】证明:∵四边形是菱形,
∴,
∴,
又∵,
∴,
∴.
在和中,
,
∴,
∴.
【解析】【分析】根据菱形的性质可得AB=BC,∠BAE=∠DAE=∠DCA=∠BCF,由垂直的概念可得∠AMB=∠CNB=90°,根据同角的余角相等可得∠ABE=∠CBF,证明△ABE≌△CBF,据此可得结论.
19.【答案】(1)解:如图,为所作;
(2)解:如图,为所作;
【解析】【分析】根据要求作出图象即可。
20.【答案】(1)解:∵BD为直径,
∴∠BAD=∠BCD=90°,
∵CD=12cm,BC=5cm,
∴BD=13(cm),
∵AC平分∠BCD,
∴∠ABD=∠ADB=45°,
∴AB=AD,
∴AB=AD=BD=,故AB的长为
(2)证明:将△ACD绕点A顺时针旋转90°后可得△ABC′,
由旋转性质可得:△ACD△ABC′,∠CAC′=90°,CA=C′A,
∴AC′=AC,CD=BC′,∠ADC=ABC′,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC+∠AD′B=180°,
又∵∠CAC′=90°,CA=C′A,
∴△C′AC是等腰直角三角形,
∴CC′=,
∴BC+C′B=,
∴BC+CD=.
【解析】【分析】(1)因为AC平分,同一个圆内圆周角度数相同对应的弦长也相同,所以AB=AD,为等腰直角三角形,根据已知条件,利用勾股定理就可以求出AB
(2)顺时针旋转90°,根据旋转的性质得到 ∠CAC′=90°,CA=C′A , CD=BC′,∠ADC=ABC ,再证明C'在CB的延长线上,于是判断为等腰直角,从而证明。
21.【答案】(1)解:a= ×(80×2+85×2+90×3+95×3+100)=89,b=90
(2)解:七,八年级学生成绩的中位数与众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更整齐,
∴八年级学生成绩较好.
【解析】【分析】(1)根据平均数和众数的定义求解即可;(2)从平均数、中位数及方差的意义求解即可.
22.【答案】(1)解:根据题意得: ,
解得:m=3500,经检验是原方程的根且符合题意;
共采购原料= 吨
(2)解:设加工成A,B型产品每天所需的原料数分别是x,y吨,
则 ,解得: ;
答:加工成A,B型产品每天所需的原料数分别是8吨、12吨。
(3)解:设加工成A型产品的原料数为a吨,总利润为y元,
则: ,解得:a≤120;
又y=1000a+600(300-a)=400a+180000
∵y随着a的增大而增大,∴当a=120时,获得最大利润;
∴原料120吨加工成A型产品,原料180吨加工成B型产品
【解析】【分析】(1)根据总价除以单价等于数量得出,第一次采购的数量为吨,第二次采购的数量为吨,根据 第二次的采购数量是第一次采购数量的两倍列出方程,求解并检验即可;
(2) 设加工成A,B型产品每天所需的原料数分别是x,y吨 ,根据 加工A型产品与B型产品各1天共需用原料数为20吨 及 加工3天A型产品与加工2天B型产品所需用原料数相等 列出方程,求解即可;
(3) 设加工成A型产品的原料数为a吨,总利润为y元, 则a吨原材料加工成A产品的时间为天,(300-a)吨原材料加工成B产品的时间为天,根据加工A产品的时间+加工B产品的时间 不超过30天 列出不等式,求解即可得出a的取值范围;根据销售A产品的利润+销售B产品的利润等于总利润建立出y与a的函数关系式,根据所得函数的性质即可解决问题。
23.【答案】(1)解:由题意:A(1,18),
把A(1,18)代入得18=,
解得k=18;
(2)解:当v=5,t=1时,h=6t2=6,l=vt=5,
xM=1+5=6,yM=18-6=12,即M(6,12),
把x=6代入得y=3≠12,
∴运动员不在滑道上
(3)解:由题意知h甲=18-4.5=6t2,
解得:t=1.5;
∵,
∴1.5(v乙-5)=4.5,解得v乙=8
答:t的值为1.5,运动员乙离开A的速度为8米/秒.
【解析】【分析】(1)把A(1,18)代入中,求出k值;
(2)先求出M坐标,再将其代入 中检验即可;
(3) 由题意知h甲=18-4.5=6t2,解得t=1.5,根据建立方程,求解即可.
24.【答案】(1)解: ,
.
(2)解: ,
,
①当 时,如图1,
,
,
.
②当 时,如图2.
过 作 ,
∵AD=BD,∠BAO=90°,
∴BF=AF,DF∥OA,
为 的中点,
,
,
.
③当 时,如图3.
过 作 ,
设 ,则 ,
由勾股定理得 ,
解得 或 .
(舍去)或 ,
.
综上所述, 或 或 .
(3)解:分别过点 作 的垂线段,垂足为 ,如图4.
,
,
,
,
,
,
即 ,
, .
设半径为 ,
,
.
又 ,在 范围内,
∴当 时, 取得最大值,此时, .
取到最大值时 的长为 .
【解析】【分析】(1)在Rt△BAO中利用余弦三角函数即可求出AB的长;
(2)首先利用勾股定理求出OA的长,然后分三种情况讨论,即 ①当 时, 先求出OD的长,则半径OC长可求,然后根据线段的和差关系即可求出AC的长; ②当 时,过作 , 根据三角形的中位线定理求出OD的长,则AC长可求; ③当 时,过 作 , 设,在Rt△DGO中利用勾股定理列式求出OD长,则AC长可求;
(3) 分别过点 作 的垂线段,垂足为 , 先证明△AMD∽△OND,利用相似三角形的性质得出AD·DN=DM·OD,设圆的半径为r,用圆的半径表示出AD和DE的乘积,构造二次函数求解即可.
1 / 1
同课章节目录
