图形的全等 复习课

课件15张PPT。 全等三角形 (复习 课)
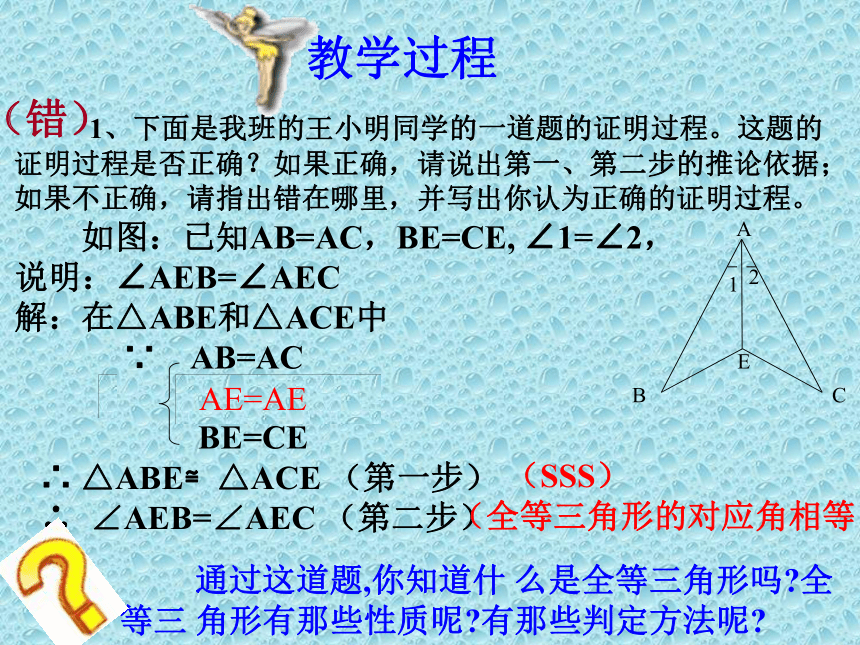
赞化学校 朱爱华一、? 复习目标与要求1、了解全等形、全等三角形的概念和性质；2、能够辨认全等三角形中对应的元素；3、会正确使用全等符号“≌”标注两个三角形全等；4、能灵活运用“SAS”、“ASA”、“AAS”、 “SSS”、5、会用三角形全等的条件推理和计算有关问“HL”判定三角形全等； 题；教学过程 1、下面是我班的王小明同学的一道题的证明过程。这题的证明过程是否正确？如果正确，请说出第一、第二步的推论依据；如果不正确，请指出错在哪里，并写出你认为正确的证明过程。 如图：已知AB=AC，BE=CE, ∠1=∠2，
说明：∠AEB=∠AEC
解：在△ABE和△ACE中
∵ AB=AC
∠1=∠2
BE=CE
∴ △ABE≌△ACE （第一步）
∴ ∠AEB=∠AEC （第二步） （错）（SSS）（全等三角形的对应角相等）∠1=∠2 × AE=AE 通过这道题,你知道什 么是全等三角形吗?全
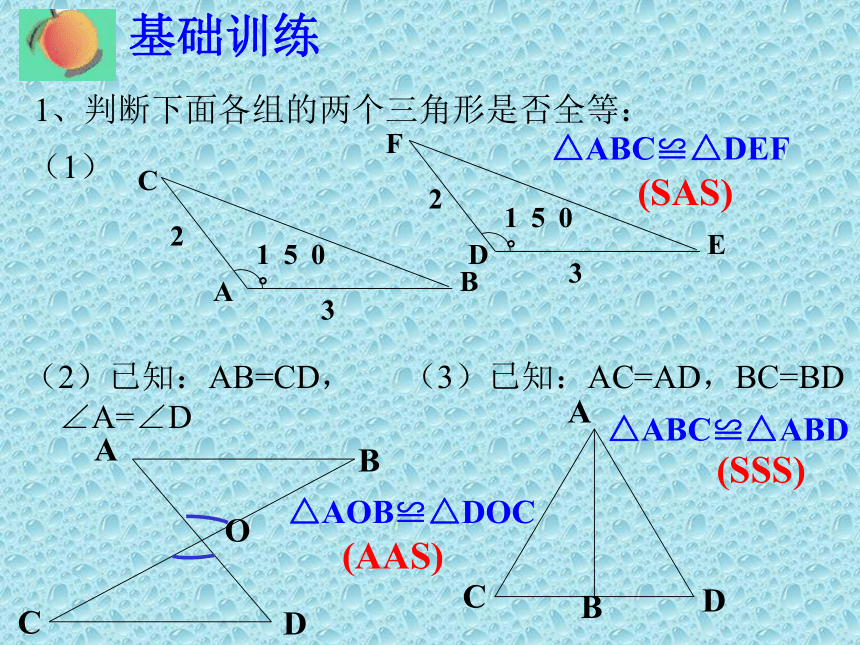
等三 角形有那些性质呢?有那些判定方法呢? 复习知识与要点能够完全重合的两个三角形，叫做全等三角形。 （1）对应边相等 （2）对应角相等1、全等三角形的概念：2、全等三角形的性质：3、全等三角形的判定方法：（1）SAS：（2）AAS：（4）SSS：（3）ASA：（5）HL有两边和它们的夹角对应相等的两个三角形全等有两个角和其中一角的对边对应相等的两个三角形全等有两个角和它们的夹边对应相等的两个三角形全等三边对应相等的两个三角形全等有斜边和一条直角边对应相等的两个直角三角形全等基础训练1、判断下面各组的两个三角形是否全等： （1） （2）已知：AB=CD， （3）已知：AC=AD，BC=BD
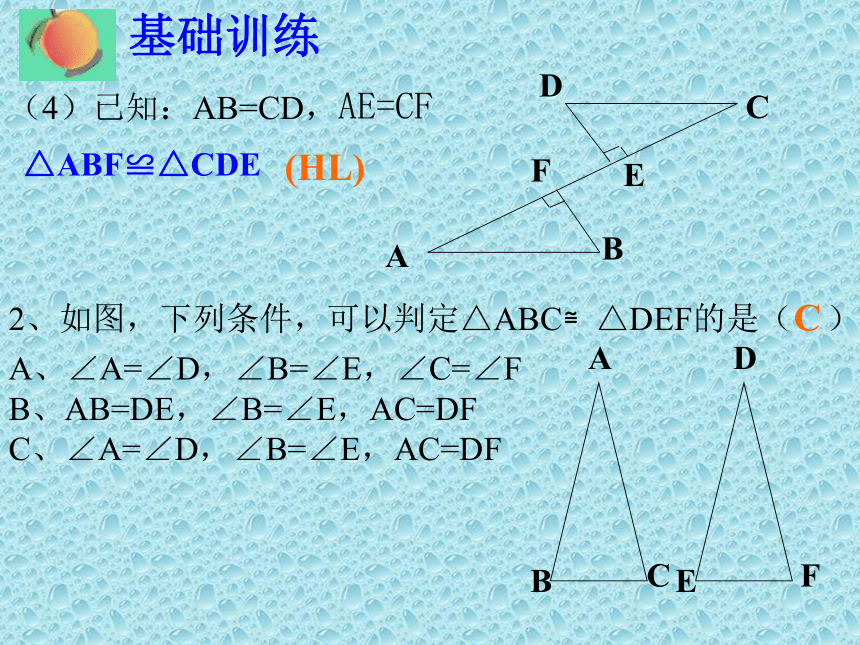
∠A=∠D(SAS) (AAS)(SSS)△ABC≌△DEF △AOB≌△DOC △ABC≌△ABD 基础训练（4）已知：AB=CD，AE=CF2、如图，下列条件，可以判定△ABC≌△DEF的是（ ）A、∠A=∠D，∠B=∠E，∠C=∠F
B、AB=DE，∠B=∠E，AC=DF
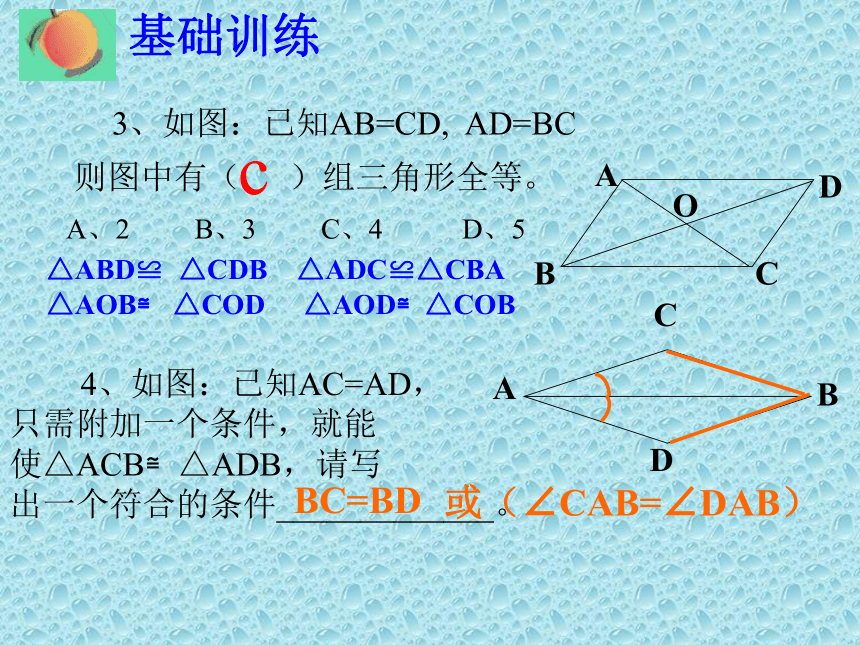
C、∠A=∠D，∠B=∠E，AC=DF (HL) △ABF≌△CDE C 基础训练 3、如图：已知AB=CD, AD=BC
则图中有（ ）组三角形全等。
A、2 B、3 C、4 D、5 4、如图：已知AC=AD，
只需附加一个条件，就能
使△ACB≌△ADB，请写
出一个符合的条件_____________。
△ABD≌ △CDB
△AOB≌ △COD△ADC≌△CBA
△AOD≌△COB
BC=BD 或（∠CAB=∠DAB） c基础训练 5、已知：AB=AC，AD=AE，试说明：△ABE≌△ACD解：在△ABE和△ACD中∵∴AB=AC
∠A=∠A
AＥ=AＤ△ABE≌△ACD　（ＳＡＳ）比一比,看谁方法多 1、已知：在AB、AC上各取一点D、E，使AD=AE，
连结BE、 CD相交于点O，∠1=∠2，试说明：∠B=∠C已知：
AO=AO
∠1=∠2已知：
AD=AE
∠DAC=∠EAB已知：
∠DOB=∠EOC 1、已知：在AB、AC上各取一点D、E，使AD=AE，
连结BE、 CD相交于点O，∠1=∠2，试说明：∠B=∠CAD=AE ∠1=∠2 AO=AO∠DOB=∠EOC在△AOD和△AOE 中∴ △AOD≌△AOE (SAS)∴ ∠DOA=∠EOA在△AOB和△AOC 中∴ ∠AOB=∠AOC∠1=∠2 AO=AO ∠ AOB= ∠ AOC ∴ △AOB≌△AOC (ASA) ∴ ∠B=∠C又∵已知解：还有更好的证明方法吗？试一试,你准行 2、已知：AB=AC，EB=EC，AE的延长线交BC于D，
试说明：BD=CD解：在△ABE和△ACE中
AB=AC，EB=EC，AE=AE
∴ △ABE≌△ACE (SSS)
∴∠BAE＝∠CAE
在△ABD和△ACD中
∵AB=AC ∠BAE= ∠CAE AD=AD
∴ △ABD≌ △ACD (SAS )
∴ BD = CD议一议如图,在△ABC中, ∠ACB=90°,AO是角平分线,点D在AC的延长线上,DE过点O且DE⊥AB,垂足为E.
(1) 请你找出图中一对相等的线段,并说明它们相等的理由; 解：∵∠ACB=90°
∴BC⊥AC
∵AO平分∠BAC
又DE⊥AB BC⊥AC
∴OE=OC（角平分线上的点到角两边的距离相等 （2）图中共有多少对相等线段，一一把它们找出来，
并说明理由 课堂小结与课外作业（3）全等三角形的判定方法； （1）全等三角形的概念；（2）全等三角形的性质；1、小结：2、作业
书P158 . 5, 6, 7, 8. 再见！欢
迎
大
家
批
评
指
正
！