解决问题专项:分数加法和减法-小学数学五年级下册苏教版(含答案)
文档属性
| 名称 | 解决问题专项:分数加法和减法-小学数学五年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
解决问题专项:分数加法和减法-小学数学五年级下册苏教版
1.一节课有40分钟。同学们合作探究用了15分钟,老师讲解用了小时,其余时间用来做练习。
(1)合作探究用了( )小时。
(2)做练习用了多少小时?
2.修一条路,甲队先修了全长的,乙队接着修了全长的。剩下的两队合修,两队合修了全长的几分之几?
3.一根彩带两次用完,第一次用去全长的,第二次用去米,哪一次用去的长一些?请简要说明理由。(可以画图)
4.淘气过生日,妈妈买了一个蛋糕。爸爸吃了,妈妈和淘气各吃了,三人共吃了这个蛋糕的几分之几?估计一下,剩下的蛋糕比多还是比少?
5.李明用一根1m长的铁丝围了一个三角形,量得三角形一边是m,另一边是m,第三条边长多少米,它是一个什么三角形?
6.一次数学竞赛,结果参赛的学生中有得优,得良,得中,其余得差,已知参加竞赛的学生不满50人,得差的学生的人数是几人?
7.江苏省盐城市的何首乌产量居全国第一,据了解2018年春季产量占全年的,夏季产量占全年的,春季和夏季产量一共占全年的几分之几?
8.蔬菜批发市场昨天卖出青萝卜吨,红萝卜吨,白菜吨,卖出的萝卜比白菜多多少吨?
9.一节课有小时,教师讲授新知大约占了全部时间的,学生小组活动大约用了全部时间的,其余的时间是自主测试。自主测试大约占全部时间的几分之几?
10.修一条千米长的公路,第一天修了全长的,第二天比第一天多修了全长的。第二天修了全长的几分之几?还剩下全长的几分之几没有修?
11.小娟和爸爸去登山,先用小时走了全程的,又用15分钟走了剩下的一半。已经走了多少小时?还剩全程的几分之几没有走?
12.甲乙两筐苹果,甲筐重千克,从甲筐中取出千克放入乙筐,两筐苹果一样重。乙筐原有多少千克苹果?两筐苹果一共多少千克?
13.一个等腰三角形,其中两条边的长度分别是米和米,它的周长是多少米?
14.有一批零件,李师傅完成,王师傅完成,这两个师傅一共完成这批零件的几分之几?
15.
(1)从健身中心经过学校到图书馆,一共要行多少千米?
(2)从健身中心到学校比从图书馆到学校少行多少千米?
16.有三根跳绳,第一根比第二根短米,第三根比第二根短米。第三根和第一根跳绳哪根长?比另一根长多少米?
17.化肥厂计划运进原料万吨,结果第一次运进万吨,第二次运进万吨,则两次运进的原料超过计划多少万吨?
18.本场数学考试时间设定为小时,当你做到此题时,估计时间已经过去了, 照此推算,你下面可用的时间占本场考试总时间的几分之几?
19.修一条千米长的路,两天一共修了全长的几分之几?
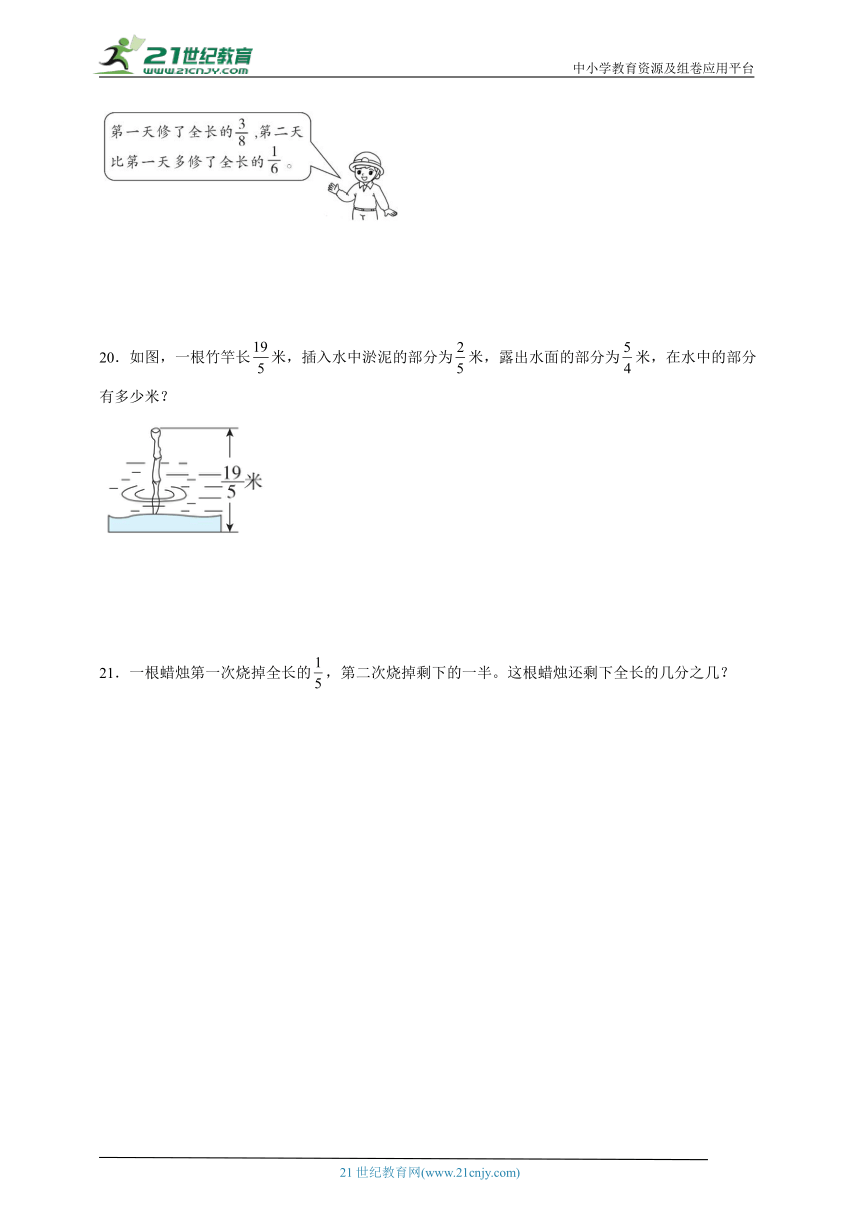
20.如图,一根竹竿长米,插入水中淤泥的部分为米,露出水面的部分为米,在水中的部分有多少米?
21.一根蜡烛第一次烧掉全长的,第二次烧掉剩下的一半。这根蜡烛还剩下全长的几分之几?
参考答案:
1.(1)
(2)小时
【分析】(1)先把15分钟化为小时为单位的数,1时=60分,用15÷60,即可解答;
(2)把40分钟化为以小时为单位的数,再根据分数减法的意义依次减去合作探究用的时间、老师讲解的时间,即可解答。
【详解】(1)1小时=60分
15÷60=(小时)
答:合作探究用了小时。
(2)40÷60=(小时)
--
=--
=-
=(小时)
答:做练习用了小时。
【点睛】本题考查单位名数的互换,低价单位化成高级点位除以进率,高级单位化成低级单位乘进率,以及分数减法的计算能力。
2.
【分析】把这条路的全长看作单位“1”,减去甲先修的,再减去乙接着修的即可。
【详解】
= -
=
答:两队合修了全长的。
【点睛】此题考查了异分母分数的连减运算,用分母的最小公倍数作公分母通分计算即可。
3.见详解
【分析】全长的和米不能直接比较。一根彩带两次用完,第一次用去全长的,那么可以先求出第二次用去全长的几分之几,再进行比较。
【详解】第二次用去的长一些。理由如下:把“全长”看作单位“1”,第一次用去全长的,第二次用去的是剩下部分,是全长的1-=,<,所以第二次用去的长一些。
画图:
【点睛】本题考查分数意义的应用。根据“一根彩带两次用完”这一信息求出第二次用去全长的几分之几是解题的关键。
4.;比少
【分析】三人一共吃了蛋糕的几分之几等于三人各自吃的蛋糕几分之几之和。根据分数的意义,来估计剩下的蛋糕比多还是比少。
【详解】
=
=;
把蛋糕分成4份,妈妈和淘气各吃了,如果爸爸也吃,那么剩下的正好是,实际上爸爸吃的比多,所以剩下的就比少。
答:三人共吃了这个蛋糕的,剩下的蛋糕比少 。
【点睛】此题考查了异分母分数连加的实际应用以及分数的意义,计算时用分数的最小公倍数做分母,最后结果要化到最简。
5.米 等腰三角形
【分析】根据题意知道1米是围成的三角形的周长,用周长减去两条边的长度就是第三条边的长度;根据边的长度的特点判断三角形的形状.
【详解】1﹣﹣=(米),
因为有两条边的长度相等,所以此三角形是等腰三角形.
答:第三条边长米;按边分它是一个等腰三角形.
6.1人
【详解】试题分析:首先把全班人数看作单位“1”,再把,,,进行通分,首先找分母7、3、2的最小公倍数,2、3、7又两两互质所以7、3、2的最小公倍数是2×3×7=42,
再通分,又知学生数不满50人,得出总人数,由此可求出得差的学生的人数.
解:首先找分母7、3、2的最小公倍数,
++=++=,
1﹣=又因为总人数不到50人,人数只能为整数获下的占;所以总人数为42人,
42×=1(人);
答:得差的学生的人数是的为1人.
点评:此题主要是把全班人数看作单位“1”,再求出题里分数中分母的最小公倍数,从而求出得差占的几分之几,一定要注意不满50人,就解决了.
7.
【分析】用春季产量的分率加上夏季产量的分率就是春夏两季一共占全年的分率。
【详解】+
=
=
答:春季和夏季产量一共占全年的。
【点睛】本题考查的是分数的加法,异分母分数相加减,先通分,然后再计算。
8.吨
【分析】青萝卜的吨数+红萝卜的吨数-白菜的吨数,即为卖出的萝卜比白菜多的吨数。
【详解】+-
=+-
=(吨)
答:卖出的萝卜比白菜多吨。
【点睛】异分母分数相加 减,要先通分,再按照同分母分数加减法的方法进行计算。
9.
【分析】把一节课的总时间看作单位“1”,用单位“1”减去教师讲授新知的时间,再减去学生小组活动所用的时间,剩下的就是自主测试所占的时间。
【详解】1--
=1-
=
答:自主测试大约占全部时间的。
【点睛】找准单位“1”是解决此题的关键,注意区分具体的量和分率。
10.;
【分析】把这条公路看成单位“1”,找出题目所给信息之间的等量关系,第一天修了全长的,第二天比第一天多修了全长的,则第二天修的分率=+,剩下的分率=1-(第一天已修分率+第二天已修分率),据此即可解答。
【详解】第二天:+=+=
剩下的: 1--
=1--
=-
=
答:第二天修了全长的,还剩下全长的没有修。
【点睛】此题考查单位“1”判断和分率的计算,熟练掌握分数加减法运算才是解题的关键。
11.小时;
【分析】第一小问要把分钟换成小时,才能够进行相加;
第二问要求还剩全程的几分之几,把全程看做单位“1”,减去第一次和第二次走的路程的占比和就是还剩全程的几分之几。但第二次走的路程是剩下的一半,所以要把第一次走后剩下的路程求出来,再利用分数的意义可以得出第二次走的路程的占比。
【详解】15分钟=小时
(小时)
的一半是
1-
答:已经走了小时,还剩全程的没有走。
【点睛】此题考查异分母分数加减法以及分数的意义,注意后来走的是剩下的一半也就是的一半,认真读题解答即可。
12.千克;千克
【分析】从甲筐中取出千克放入乙筐后,则现在的甲=-,现在的乙=原来的乙+,又因为现在两筐一样重,所以-=原来的乙+,说明原来的甲比原来的乙多了2个,用减去2个,即可求出原来的乙,进而可以求出原有甲乙的总重量。
【详解】--=(千克);
+=(千克)
答:乙筐原有千克,两筐苹果一共千克。
【点睛】理解原有甲、乙两筐到底相差多少是解决此题的关键,同时注意异分母加减法的运算方法。
13.米
【分析】根据“三角形的任意两边之和大于第三边”,如果腰是米,根据等腰三角形的特点,则三角形的三边分别是米、米和米,米+米>米,即任意两边之和大于第三边,所以能够成三角形,再把三边加起来即可求出周长;如果腰是米,则三角形的三边分别是米,米和米,米+米=米,不能围成三角形。
【详解】米+米>米,能构成三角形,
三角形的周长=(米)
答:它的周长是米。
【点睛】掌握三角形的特性:三角形的任意两边长度和大于第三边。
14.
【分析】单位“1”相同,李师傅完成这批零件的分率+王师傅完成这批零件的分率即可。
【详解】+
=
=
答:这两个师傅一共完成这批零件的。
【点睛】此题主要考查了异分母分数的加法计算,两个分数分母的最小公倍数做公分母,通分计算。
15.(1)千米
(2)千米
【分析】(1)健身中心到学校的距离+学校到图书馆的距离即为一共要行多少千米;
(2)图书馆到学校的距离-健身中心到学校的距离即为少行多少千米。
【详解】(1)=(千米)
答:一共要行千米。
(2)=(千米)
答:从健身中心到学校比从图书馆到学校少行千米。
【点睛】异分母分数相加 减,要先通分,再按照同分母分数加减法的方法进行计算。
16.第一根;米
【分析】把第二根绳子的长度设为1米,由此求出第一根与第三根绳子的长度,然后再进行比较,据此解答。
【详解】假设第二根绳子的长度是1米。
1-=(米)
1-=(米)
因为>,所以第一根跳绳长。
-
=
=(米)
答:第一根跳绳长,比另一根长米。
【点睛】解答此题的关键是假设第二根绳子一个具体的长度,再根据数量之间的关系解决问题。
17.万吨
【分析】将两次运进的原料加起来,减去计划运进的原料即可。
【详解】+-=(万吨)
答:两次运进的原料超过计划万吨。
【点睛】本题考查了分数加减混合应用题,异分母分数相加减,先通分再计算。
18.
【分析】把本场数学考试时间看作单位“1”,时间已经过去了,还剩,用减法计算。
【详解】1-=
【点睛】同分母分数加减法,要把分子相加减,分母不变。
19.
【分析】把全长看作单位“1”,第一天修了全长的,第二天修了全长的+,两天修的分率和即为两天一共修了全长的几分之几。
【详解】++
=+
=+
=
答:两天一共修了全长的。
【点睛】解答此题的关键是确定单位“1”,根据分数加法的意义求出两天一共修了全长的几分之几。
20.米
【分析】根据题意,竹竿在水中部分的长度=竹竿长度-插入淤泥部分长度-露出水面部分长度,代入数据解答即可。
【详解】--
=
=(米)
答:在水中的部分有米。
【点睛】此题中的分数后面都带有单位表示具体数值,可以直接相加减。注意通分的公分母用最小公倍数比较简便。
21.
【分析】全长-第一次烧掉的-第二次烧掉的=剩下的,据此解答。
【详解】第一次烧掉全长的,剩下全长的,的一半就是,烧掉两次后还剩下:1--=
答:这根蜡烛还剩下全长的。
【点睛】本题主要考查分数连减的简单应用,解题时注意“第二次烧掉剩下的一半”,就是全长的的一半。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
解决问题专项:分数加法和减法-小学数学五年级下册苏教版
1.一节课有40分钟。同学们合作探究用了15分钟,老师讲解用了小时,其余时间用来做练习。
(1)合作探究用了( )小时。
(2)做练习用了多少小时?
2.修一条路,甲队先修了全长的,乙队接着修了全长的。剩下的两队合修,两队合修了全长的几分之几?
3.一根彩带两次用完,第一次用去全长的,第二次用去米,哪一次用去的长一些?请简要说明理由。(可以画图)
4.淘气过生日,妈妈买了一个蛋糕。爸爸吃了,妈妈和淘气各吃了,三人共吃了这个蛋糕的几分之几?估计一下,剩下的蛋糕比多还是比少?
5.李明用一根1m长的铁丝围了一个三角形,量得三角形一边是m,另一边是m,第三条边长多少米,它是一个什么三角形?
6.一次数学竞赛,结果参赛的学生中有得优,得良,得中,其余得差,已知参加竞赛的学生不满50人,得差的学生的人数是几人?
7.江苏省盐城市的何首乌产量居全国第一,据了解2018年春季产量占全年的,夏季产量占全年的,春季和夏季产量一共占全年的几分之几?
8.蔬菜批发市场昨天卖出青萝卜吨,红萝卜吨,白菜吨,卖出的萝卜比白菜多多少吨?
9.一节课有小时,教师讲授新知大约占了全部时间的,学生小组活动大约用了全部时间的,其余的时间是自主测试。自主测试大约占全部时间的几分之几?
10.修一条千米长的公路,第一天修了全长的,第二天比第一天多修了全长的。第二天修了全长的几分之几?还剩下全长的几分之几没有修?
11.小娟和爸爸去登山,先用小时走了全程的,又用15分钟走了剩下的一半。已经走了多少小时?还剩全程的几分之几没有走?
12.甲乙两筐苹果,甲筐重千克,从甲筐中取出千克放入乙筐,两筐苹果一样重。乙筐原有多少千克苹果?两筐苹果一共多少千克?
13.一个等腰三角形,其中两条边的长度分别是米和米,它的周长是多少米?
14.有一批零件,李师傅完成,王师傅完成,这两个师傅一共完成这批零件的几分之几?
15.
(1)从健身中心经过学校到图书馆,一共要行多少千米?
(2)从健身中心到学校比从图书馆到学校少行多少千米?
16.有三根跳绳,第一根比第二根短米,第三根比第二根短米。第三根和第一根跳绳哪根长?比另一根长多少米?
17.化肥厂计划运进原料万吨,结果第一次运进万吨,第二次运进万吨,则两次运进的原料超过计划多少万吨?
18.本场数学考试时间设定为小时,当你做到此题时,估计时间已经过去了, 照此推算,你下面可用的时间占本场考试总时间的几分之几?
19.修一条千米长的路,两天一共修了全长的几分之几?
20.如图,一根竹竿长米,插入水中淤泥的部分为米,露出水面的部分为米,在水中的部分有多少米?
21.一根蜡烛第一次烧掉全长的,第二次烧掉剩下的一半。这根蜡烛还剩下全长的几分之几?
参考答案:
1.(1)
(2)小时
【分析】(1)先把15分钟化为小时为单位的数,1时=60分,用15÷60,即可解答;
(2)把40分钟化为以小时为单位的数,再根据分数减法的意义依次减去合作探究用的时间、老师讲解的时间,即可解答。
【详解】(1)1小时=60分
15÷60=(小时)
答:合作探究用了小时。
(2)40÷60=(小时)
--
=--
=-
=(小时)
答:做练习用了小时。
【点睛】本题考查单位名数的互换,低价单位化成高级点位除以进率,高级单位化成低级单位乘进率,以及分数减法的计算能力。
2.
【分析】把这条路的全长看作单位“1”,减去甲先修的,再减去乙接着修的即可。
【详解】
= -
=
答:两队合修了全长的。
【点睛】此题考查了异分母分数的连减运算,用分母的最小公倍数作公分母通分计算即可。
3.见详解
【分析】全长的和米不能直接比较。一根彩带两次用完,第一次用去全长的,那么可以先求出第二次用去全长的几分之几,再进行比较。
【详解】第二次用去的长一些。理由如下:把“全长”看作单位“1”,第一次用去全长的,第二次用去的是剩下部分,是全长的1-=,<,所以第二次用去的长一些。
画图:
【点睛】本题考查分数意义的应用。根据“一根彩带两次用完”这一信息求出第二次用去全长的几分之几是解题的关键。
4.;比少
【分析】三人一共吃了蛋糕的几分之几等于三人各自吃的蛋糕几分之几之和。根据分数的意义,来估计剩下的蛋糕比多还是比少。
【详解】
=
=;
把蛋糕分成4份,妈妈和淘气各吃了,如果爸爸也吃,那么剩下的正好是,实际上爸爸吃的比多,所以剩下的就比少。
答:三人共吃了这个蛋糕的,剩下的蛋糕比少 。
【点睛】此题考查了异分母分数连加的实际应用以及分数的意义,计算时用分数的最小公倍数做分母,最后结果要化到最简。
5.米 等腰三角形
【分析】根据题意知道1米是围成的三角形的周长,用周长减去两条边的长度就是第三条边的长度;根据边的长度的特点判断三角形的形状.
【详解】1﹣﹣=(米),
因为有两条边的长度相等,所以此三角形是等腰三角形.
答:第三条边长米;按边分它是一个等腰三角形.
6.1人
【详解】试题分析:首先把全班人数看作单位“1”,再把,,,进行通分,首先找分母7、3、2的最小公倍数,2、3、7又两两互质所以7、3、2的最小公倍数是2×3×7=42,
再通分,又知学生数不满50人,得出总人数,由此可求出得差的学生的人数.
解:首先找分母7、3、2的最小公倍数,
++=++=,
1﹣=又因为总人数不到50人,人数只能为整数获下的占;所以总人数为42人,
42×=1(人);
答:得差的学生的人数是的为1人.
点评:此题主要是把全班人数看作单位“1”,再求出题里分数中分母的最小公倍数,从而求出得差占的几分之几,一定要注意不满50人,就解决了.
7.
【分析】用春季产量的分率加上夏季产量的分率就是春夏两季一共占全年的分率。
【详解】+
=
=
答:春季和夏季产量一共占全年的。
【点睛】本题考查的是分数的加法,异分母分数相加减,先通分,然后再计算。
8.吨
【分析】青萝卜的吨数+红萝卜的吨数-白菜的吨数,即为卖出的萝卜比白菜多的吨数。
【详解】+-
=+-
=(吨)
答:卖出的萝卜比白菜多吨。
【点睛】异分母分数相加 减,要先通分,再按照同分母分数加减法的方法进行计算。
9.
【分析】把一节课的总时间看作单位“1”,用单位“1”减去教师讲授新知的时间,再减去学生小组活动所用的时间,剩下的就是自主测试所占的时间。
【详解】1--
=1-
=
答:自主测试大约占全部时间的。
【点睛】找准单位“1”是解决此题的关键,注意区分具体的量和分率。
10.;
【分析】把这条公路看成单位“1”,找出题目所给信息之间的等量关系,第一天修了全长的,第二天比第一天多修了全长的,则第二天修的分率=+,剩下的分率=1-(第一天已修分率+第二天已修分率),据此即可解答。
【详解】第二天:+=+=
剩下的: 1--
=1--
=-
=
答:第二天修了全长的,还剩下全长的没有修。
【点睛】此题考查单位“1”判断和分率的计算,熟练掌握分数加减法运算才是解题的关键。
11.小时;
【分析】第一小问要把分钟换成小时,才能够进行相加;
第二问要求还剩全程的几分之几,把全程看做单位“1”,减去第一次和第二次走的路程的占比和就是还剩全程的几分之几。但第二次走的路程是剩下的一半,所以要把第一次走后剩下的路程求出来,再利用分数的意义可以得出第二次走的路程的占比。
【详解】15分钟=小时
(小时)
的一半是
1-
答:已经走了小时,还剩全程的没有走。
【点睛】此题考查异分母分数加减法以及分数的意义,注意后来走的是剩下的一半也就是的一半,认真读题解答即可。
12.千克;千克
【分析】从甲筐中取出千克放入乙筐后,则现在的甲=-,现在的乙=原来的乙+,又因为现在两筐一样重,所以-=原来的乙+,说明原来的甲比原来的乙多了2个,用减去2个,即可求出原来的乙,进而可以求出原有甲乙的总重量。
【详解】--=(千克);
+=(千克)
答:乙筐原有千克,两筐苹果一共千克。
【点睛】理解原有甲、乙两筐到底相差多少是解决此题的关键,同时注意异分母加减法的运算方法。
13.米
【分析】根据“三角形的任意两边之和大于第三边”,如果腰是米,根据等腰三角形的特点,则三角形的三边分别是米、米和米,米+米>米,即任意两边之和大于第三边,所以能够成三角形,再把三边加起来即可求出周长;如果腰是米,则三角形的三边分别是米,米和米,米+米=米,不能围成三角形。
【详解】米+米>米,能构成三角形,
三角形的周长=(米)
答:它的周长是米。
【点睛】掌握三角形的特性:三角形的任意两边长度和大于第三边。
14.
【分析】单位“1”相同,李师傅完成这批零件的分率+王师傅完成这批零件的分率即可。
【详解】+
=
=
答:这两个师傅一共完成这批零件的。
【点睛】此题主要考查了异分母分数的加法计算,两个分数分母的最小公倍数做公分母,通分计算。
15.(1)千米
(2)千米
【分析】(1)健身中心到学校的距离+学校到图书馆的距离即为一共要行多少千米;
(2)图书馆到学校的距离-健身中心到学校的距离即为少行多少千米。
【详解】(1)=(千米)
答:一共要行千米。
(2)=(千米)
答:从健身中心到学校比从图书馆到学校少行千米。
【点睛】异分母分数相加 减,要先通分,再按照同分母分数加减法的方法进行计算。
16.第一根;米
【分析】把第二根绳子的长度设为1米,由此求出第一根与第三根绳子的长度,然后再进行比较,据此解答。
【详解】假设第二根绳子的长度是1米。
1-=(米)
1-=(米)
因为>,所以第一根跳绳长。
-
=
=(米)
答:第一根跳绳长,比另一根长米。
【点睛】解答此题的关键是假设第二根绳子一个具体的长度,再根据数量之间的关系解决问题。
17.万吨
【分析】将两次运进的原料加起来,减去计划运进的原料即可。
【详解】+-=(万吨)
答:两次运进的原料超过计划万吨。
【点睛】本题考查了分数加减混合应用题,异分母分数相加减,先通分再计算。
18.
【分析】把本场数学考试时间看作单位“1”,时间已经过去了,还剩,用减法计算。
【详解】1-=
【点睛】同分母分数加减法,要把分子相加减,分母不变。
19.
【分析】把全长看作单位“1”,第一天修了全长的,第二天修了全长的+,两天修的分率和即为两天一共修了全长的几分之几。
【详解】++
=+
=+
=
答:两天一共修了全长的。
【点睛】解答此题的关键是确定单位“1”,根据分数加法的意义求出两天一共修了全长的几分之几。
20.米
【分析】根据题意,竹竿在水中部分的长度=竹竿长度-插入淤泥部分长度-露出水面部分长度,代入数据解答即可。
【详解】--
=
=(米)
答:在水中的部分有米。
【点睛】此题中的分数后面都带有单位表示具体数值,可以直接相加减。注意通分的公分母用最小公倍数比较简便。
21.
【分析】全长-第一次烧掉的-第二次烧掉的=剩下的,据此解答。
【详解】第一次烧掉全长的,剩下全长的,的一半就是,烧掉两次后还剩下:1--=
答:这根蜡烛还剩下全长的。
【点睛】本题主要考查分数连减的简单应用,解题时注意“第二次烧掉剩下的一半”,就是全长的的一半。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
