6.2.1向量的加法运算 说课稿课件(共34张PPT)
文档属性
| 名称 | 6.2.1向量的加法运算 说课稿课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 684.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 05:15:51 | ||
图片预览








文档简介
(共23张PPT)
一、教材分析
二、教学方法
三、学法指导
四、教学程序
我将从教材分析、教学方法、学法指导、教学程序四个方面
对本节课的教学进行汇报
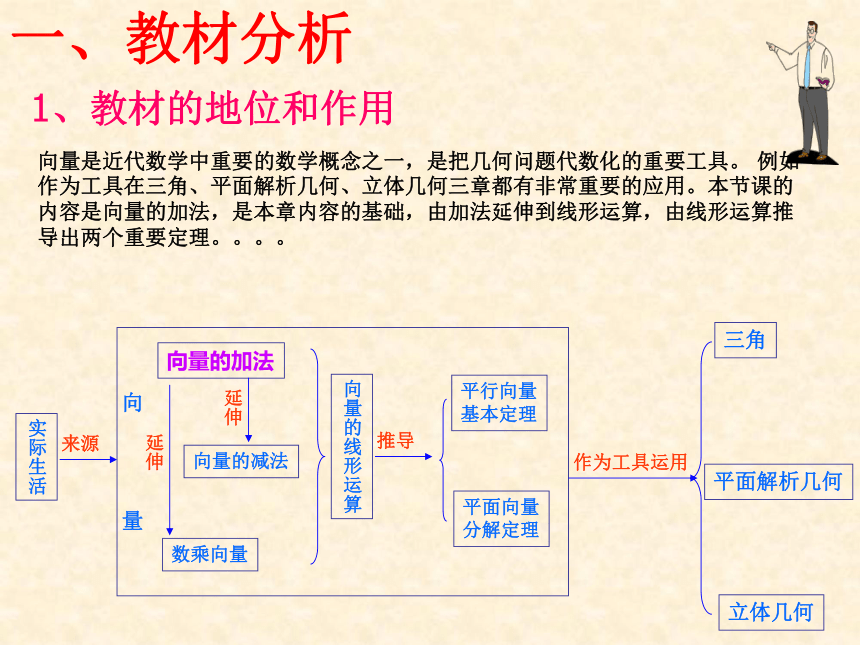
1、教材的地位和作用
一、教材分析
向量的加法
向量的减法
数乘向量
向量的线形运算
三角
平面解析几何
向 量
来源
实际生活
延伸
延伸
平行向量
基本定理
平面向量
分解定理
推导
立体几何
作为工具运用
向量是近代数学中重要的数学概念之一,是把几何问题代数化的重要工具。 例如
作为工具在三角、平面解析几何、立体几何三章都有非常重要的应用。本节课的
内容是向量的加法,是本章内容的基础,由加法延伸到线形运算,由线形运算推
导出两个重要定理。。。。
因此学好本节课将为后面学习向量的其它知识
奠定基础,为用“数”的运算解决“形”的问题
提供工具和方法。
2、教学目标
两个向量的和的概念是向量加法的基础,而向量加法是
向量其他运算的基础。
知识目标:理解向量的和,掌握向量加法的
三角形法则和平行四边形法则,向量加法的
运算律。
教学过程中,主要由学生自己动手,在解决问题的过程中发现
、归纳新知识,因此,制定能力目标为:
能力目标:提高学生观察、归纳、迁移能力和
动手能力;培养学生的转化思想。
本节课的教学从实际问题入手引出新知识,主要知识均
由学生发现、总结
德育目标:注重培养学生积极思考、勇于探索的科学精神
以及总结规律、尊重规律的观念。
本节课的知识均由学生发现、总结,在不知不觉
中提高了学生的学习兴趣,形成了良好的课堂学习气氛
情感目标: 培养学生与知识间的情感;促进学生与学生之间、
学生与老师之间的沟通、交流、合作;形成学生
间、师生间和谐、融洽、民主、互动的氛围。
3、教学重点和难点
向量加法是向量其他运算的基础,
重点:向量加法的三角形法则和平行
四边形法则,向量加法的运算律。
两个向量的和的概念是向量加法的基础,而许多学生又以为向量的和与
向量的加法是一个概念
难点:对向量和的理解。
二、教学方法
在教学过程中体现以教师为主导,学生为主体的教学思想,深化教学改革,确定本课主要的教法为:
1、引导发现法:
通过引导,由学生在自己动手解决问题的过程中发现新问题并加以解决,建构整节课的内容。
2、多媒体辅助教学:
借助多媒体引导学生观察,使问题变得直观,易于突破;同时其灵活多样的形式可以极大地提高学生的学习兴趣;其软件交互功能可以帮助教师更好地实施教学,加大一堂课的信息量,使教学目标更好的实现。
三、学法指导
现代教学论认为:教学的关键是使学生实现由“学会”到“会学”
的质的飞跃。本节课,我尝试对学生的学法作一定的指导:
1、引导学生自己发现问题、提出问题并予以解决。
2、培养学生善于从实际生活中抽象出数学模型,提高观
察、归纳、分析、总结能力。
3、逐步学会合作交流、自我认知、自我建构。
(一)导入新课
1、复习回顾:(1)向量的定义、表示方法。
(2)自由向量、相等向量。
3、多媒体演示实例
2、练习
A
.
恰当设置题目,使学生既能复习前面所学知识,又能为本节课发现新的规律奠定基础
第1.2题的目的是复习巩固上节课知识,同时为学生自己动手解决本节课问题
奠定基础
第3题是多媒体演示实例,目的:一是数学问题实际化,消除学生对纯数学研究的
恐惧心理,并培养学生用数学解决问题的思想意识,二是借助多媒体使问题变的直观
易于突破,具体问题是
一位台湾同胞要从台北到北京探亲,但因为台湾和大陆没有直航,所以他需要先从台北
到广州,再从广州到北京。这一过程中,从台北到广州,从广州到北京这两段位移
的效果相当于从台北到北京位移的效果,而位移可以看作向量,由此得出新知
(二)学习新课
1、向量的和
+
+
2、向量加法的三角形法则
强调(1)两个向量的位置关系
(2)和向量的方向
那么怎样求向量得和呢?回顾刚才得实例,分析三个向量得位置关系,得出向量
加法得三角形法则,可以由学生总结,老师加以规范,特别要强调。。。
练习1:如图:已知向量 , ,求作:
+
(1)
(4)
(3)
(2)
接着通过练习加以巩固,方式是由学生自己作图求。。。这时老师留心学生的作图
方式,有针对性的找两位同学做同一个题
3、向量加法的平行四边形法则
+
强调(1)两个向量的位置关系
(2)和向量的方向
比如,第二题,有两种作图情况
1、平移向量b,使向量b的试点
于向量a的终点重合,作出两向量
的和,
2、。。。。
通过分析得出向量加法的平行
四边形法则
规律仍由学生总结
但还是要强调
练习2:如图:已知向量 , ,求作:
+
(1)
(4)
(3)
(2)
将第一题改为利用向量加法的平行四边形法则作出两向量的和加以巩固
练习3:如图:已知平行四边形ABCD,填空
D
C
B
A
+
(1)
=
+
(2)
=
+
+
+
( )
( )
+
(4)
(5)
=
=
+
=
(3)
练习3是在给定的图形中找出与
所给向量表达式相等的向量。
目的:一是巩固所学
二是通过答案可知(1)(3)的
结果一样(4)(5)的结论一样
推广到一般情况就总结出
(2)结合律
4、向量加法的运算律
(1)交换律
+
+
=
+
+
( )
=
+
+
( )
+
+
=
注意:
=
需要强调特殊情况
练习4:如图:已知向量 , ,求作:
+
+
+
这时,给出两向量平行时,求两向量的和,本节课的内容都是由学生的自己在解决
问题时发现归纳的,所以很多同学迫不及待的自己解答,发现因为平行,不能构成
平行四边形和三角形,陷入思考,问题的解决还是要回到实际生活中,利用位移来求
和,发现符合向量加法的三角形法则规律,从而解决特殊情况的求和问题
最终总结出求两个向量和时三角形法则都适用,并推广到多个向量求和的情况
(三)归纳小结
1、一个概念: 向量的和
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
数学思想方法方面:
1、具体与抽象的数学思维方法,
2、类比的思想方法
(四)、布置作业
1、基础题目:
2、探索题目:
针对学生素质的差异进行分层训练,既能使学生掌握
基础知识,又能使学有余力的学生有所提高,
从而达到拔尖和“减负”的目的。 充分照顾到每一位学生,
体现课堂教学的公平性
(五)板书设计
向量的加法
1、向量的和
2、三角形法则
3、平行四边形法则
4、运算律
练1
练2
练3
练4
归纳小结
布置作业
教学环节
时间分配
导入新课
5分钟
学习新课
15分钟
练习反馈
20分钟
归纳小结
4分钟
布置作业
1分钟
(六)时间安排
一、教材分析
二、教学方法
三、学法指导
四、教学程序
我将从教材分析、教学方法、学法指导、教学程序四个方面
对本节课的教学进行汇报
1、教材的地位和作用
一、教材分析
向量的加法
向量的减法
数乘向量
向量的线形运算
三角
平面解析几何
向 量
来源
实际生活
延伸
延伸
平行向量
基本定理
平面向量
分解定理
推导
立体几何
作为工具运用
向量是近代数学中重要的数学概念之一,是把几何问题代数化的重要工具。 例如
作为工具在三角、平面解析几何、立体几何三章都有非常重要的应用。本节课的
内容是向量的加法,是本章内容的基础,由加法延伸到线形运算,由线形运算推
导出两个重要定理。。。。
因此学好本节课将为后面学习向量的其它知识
奠定基础,为用“数”的运算解决“形”的问题
提供工具和方法。
2、教学目标
两个向量的和的概念是向量加法的基础,而向量加法是
向量其他运算的基础。
知识目标:理解向量的和,掌握向量加法的
三角形法则和平行四边形法则,向量加法的
运算律。
教学过程中,主要由学生自己动手,在解决问题的过程中发现
、归纳新知识,因此,制定能力目标为:
能力目标:提高学生观察、归纳、迁移能力和
动手能力;培养学生的转化思想。
本节课的教学从实际问题入手引出新知识,主要知识均
由学生发现、总结
德育目标:注重培养学生积极思考、勇于探索的科学精神
以及总结规律、尊重规律的观念。
本节课的知识均由学生发现、总结,在不知不觉
中提高了学生的学习兴趣,形成了良好的课堂学习气氛
情感目标: 培养学生与知识间的情感;促进学生与学生之间、
学生与老师之间的沟通、交流、合作;形成学生
间、师生间和谐、融洽、民主、互动的氛围。
3、教学重点和难点
向量加法是向量其他运算的基础,
重点:向量加法的三角形法则和平行
四边形法则,向量加法的运算律。
两个向量的和的概念是向量加法的基础,而许多学生又以为向量的和与
向量的加法是一个概念
难点:对向量和的理解。
二、教学方法
在教学过程中体现以教师为主导,学生为主体的教学思想,深化教学改革,确定本课主要的教法为:
1、引导发现法:
通过引导,由学生在自己动手解决问题的过程中发现新问题并加以解决,建构整节课的内容。
2、多媒体辅助教学:
借助多媒体引导学生观察,使问题变得直观,易于突破;同时其灵活多样的形式可以极大地提高学生的学习兴趣;其软件交互功能可以帮助教师更好地实施教学,加大一堂课的信息量,使教学目标更好的实现。
三、学法指导
现代教学论认为:教学的关键是使学生实现由“学会”到“会学”
的质的飞跃。本节课,我尝试对学生的学法作一定的指导:
1、引导学生自己发现问题、提出问题并予以解决。
2、培养学生善于从实际生活中抽象出数学模型,提高观
察、归纳、分析、总结能力。
3、逐步学会合作交流、自我认知、自我建构。
(一)导入新课
1、复习回顾:(1)向量的定义、表示方法。
(2)自由向量、相等向量。
3、多媒体演示实例
2、练习
A
.
恰当设置题目,使学生既能复习前面所学知识,又能为本节课发现新的规律奠定基础
第1.2题的目的是复习巩固上节课知识,同时为学生自己动手解决本节课问题
奠定基础
第3题是多媒体演示实例,目的:一是数学问题实际化,消除学生对纯数学研究的
恐惧心理,并培养学生用数学解决问题的思想意识,二是借助多媒体使问题变的直观
易于突破,具体问题是
一位台湾同胞要从台北到北京探亲,但因为台湾和大陆没有直航,所以他需要先从台北
到广州,再从广州到北京。这一过程中,从台北到广州,从广州到北京这两段位移
的效果相当于从台北到北京位移的效果,而位移可以看作向量,由此得出新知
(二)学习新课
1、向量的和
+
+
2、向量加法的三角形法则
强调(1)两个向量的位置关系
(2)和向量的方向
那么怎样求向量得和呢?回顾刚才得实例,分析三个向量得位置关系,得出向量
加法得三角形法则,可以由学生总结,老师加以规范,特别要强调。。。
练习1:如图:已知向量 , ,求作:
+
(1)
(4)
(3)
(2)
接着通过练习加以巩固,方式是由学生自己作图求。。。这时老师留心学生的作图
方式,有针对性的找两位同学做同一个题
3、向量加法的平行四边形法则
+
强调(1)两个向量的位置关系
(2)和向量的方向
比如,第二题,有两种作图情况
1、平移向量b,使向量b的试点
于向量a的终点重合,作出两向量
的和,
2、。。。。
通过分析得出向量加法的平行
四边形法则
规律仍由学生总结
但还是要强调
练习2:如图:已知向量 , ,求作:
+
(1)
(4)
(3)
(2)
将第一题改为利用向量加法的平行四边形法则作出两向量的和加以巩固
练习3:如图:已知平行四边形ABCD,填空
D
C
B
A
+
(1)
=
+
(2)
=
+
+
+
( )
( )
+
(4)
(5)
=
=
+
=
(3)
练习3是在给定的图形中找出与
所给向量表达式相等的向量。
目的:一是巩固所学
二是通过答案可知(1)(3)的
结果一样(4)(5)的结论一样
推广到一般情况就总结出
(2)结合律
4、向量加法的运算律
(1)交换律
+
+
=
+
+
( )
=
+
+
( )
+
+
=
注意:
=
需要强调特殊情况
练习4:如图:已知向量 , ,求作:
+
+
+
这时,给出两向量平行时,求两向量的和,本节课的内容都是由学生的自己在解决
问题时发现归纳的,所以很多同学迫不及待的自己解答,发现因为平行,不能构成
平行四边形和三角形,陷入思考,问题的解决还是要回到实际生活中,利用位移来求
和,发现符合向量加法的三角形法则规律,从而解决特殊情况的求和问题
最终总结出求两个向量和时三角形法则都适用,并推广到多个向量求和的情况
(三)归纳小结
1、一个概念: 向量的和
2、两个法则: 向量加法的三角形法则和平行四边形法则
3、两条运算律: 向量加法的交换律
结合律
+
+
=
+
+
( )
=
+
+
( )
知识方面:
+
+
=
=
数学思想方法方面:
1、具体与抽象的数学思维方法,
2、类比的思想方法
(四)、布置作业
1、基础题目:
2、探索题目:
针对学生素质的差异进行分层训练,既能使学生掌握
基础知识,又能使学有余力的学生有所提高,
从而达到拔尖和“减负”的目的。 充分照顾到每一位学生,
体现课堂教学的公平性
(五)板书设计
向量的加法
1、向量的和
2、三角形法则
3、平行四边形法则
4、运算律
练1
练2
练3
练4
归纳小结
布置作业
教学环节
时间分配
导入新课
5分钟
学习新课
15分钟
练习反馈
20分钟
归纳小结
4分钟
布置作业
1分钟
(六)时间安排
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
