6.2.1向量的加法运算 说课课件(共26张PPT)
文档属性
| 名称 | 6.2.1向量的加法运算 说课课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 05:32:49 | ||
图片预览





文档简介
(共26张PPT)
向量的加法运算
人教A版 必修第二册
教材分析
教法学法
过程设计
课后反思
说课流程
(一)教材的地位及前后联系
向量是沟通代数、几何与三角函数的重要工具.
本节课是向量运算的起始课,为后继学习向量的其他运算以及空间向量奠定了基础.
本节内容在教材中占有极其重要的地位,在知识体系上起着承上启下的作用.
一、教材分析
1
知识目标
2
能力目标
3
情感目标
(二)教育教学目标
(三)教学重点难点
重点
两个向量的和的概念及其几何意义.
动手操作验证向量加法的运算律.
难点
学情分析:
物理学中位移和力等知识的学习,为学生学习本节课提供了知识背景.
二、教法学法设计
教学方法:
学习方法: 类比、迁移、分类、归纳.
教学手段:多媒体辅助教学.
启发-探究.
复习引入
作业推荐
法则探究
定义建构
运算律探究
学生总结
新知应用
三、教学过程设计
(一)复习引入
1.向量的概念及表示方法?
2.什么叫相等向量?
3.什么叫共线向量?
问题1 两个实数能进行加法运算,那么,
向量是否也能进行加法运算?
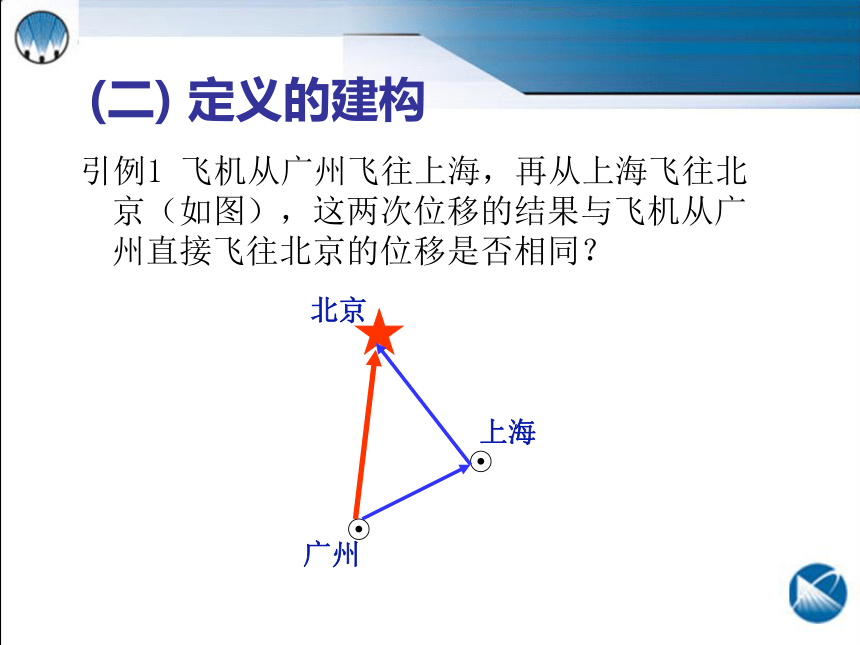
(二) 定义的建构
引例1 飞机从广州飞往上海,再从上海飞往北京(如图),这两次位移的结果与飞机从广州直接飞往北京的位移是否相同?
广州
上海
北京
(二) 定义的建构
引例2 求弹簧所受的拉力的合力
问题2 请结合“合位移”问题和“弹簧所受拉力的合力”问题,
试着给出向量加法的定义.
(三) 法则的探究
问题3 怎样求两个向量的和
A
a
b
B
C
a+b
a
b
三角形法则
(三) 法则的探究
A
b
B
C
a
b
平行四边形法则
a
a+b
(三) 法则的探究
2、方向相反
a
a
b
b
A
B
B
A
C
C
AC = a + b
AC = a + b
对于两个非零共线向量,能否通过两种加法法则求出他们的和?
a
b
1、方向相同
b
a
(三) 法则的探究
问题4 两种法则有何特征?
名称
运算结果
首尾关系
适用范围
向量
向量
首尾相连
任意非零向量
起点相同
不共线向量
角度
三角形法则
平行四边形法则
问题5 已知 是非零向量,则 与 之间
有什么关系?
结论 向量加法的三角形不等式
(三) 法则的探究
问题6 定义了一种新运算,自然要研究其运算律问题. 你
(四) 运算律的探究
类比旧知---猜想结论
动手操作---验证结论
能说出实数加法的运算律吗?向量的加法是否也
有运算律?有哪些运算律呢?
问题7 向量加法的交换律是否成立 请探究.
问题8 类比向量加法的交换律,向量加法的结合律是否
成立 请探究.
(四) 运算律的探究
向量加法的交换律
A
B
C
D
a
a
b
b
(四) 运算律的探究
向量加法的结合律
A
B
C
D
a
c
c
b
a
b
例2化简 (1) ; (2) ;
(3)
(五) 新知的初步应用
例1 如图,已知非零向量 ,求作向量 .
(1)
(2)
(五) 新知的初步应用
求有限个向量的和
(五) 新知的初步应用
例3 在长江南岸某渡口处,江水以12.5km/h的速 度向东流,渡船的速度为25km/h. 渡船要垂直的度过长江,其航向应如何确定.
(六)学生代表总结发言
(七) 分层次推荐作业
作业
思考题:
(1)向量的减法是如何定义的?其几何意义是什么?
(2)向量减法有哪些运算律?
(3)向量的减法与加法有何联系?
附: 板书设计
向量的加法运算
1.向量的加法定义
2.两个向量的和向量的作法
⑴平行四边形法则
⑵三角形法则
3.向量的运算律
例1
例2
引申
小结
作业
四、课后反思
通过创设问题情境, 层层设问的方式,“启发-探究”
注意讲练结合,做到教与学的有机结合.
采取小组总结发言, 提高学生的归纳、表达能力.
通过分层次推荐作业, 体现教学的巩固性和发展性原则.
的教学方法和“多媒体辅助教学”,让学生在探索中
获取和应用新知.
恳请批评指正!
谢谢!
向量的加法运算
人教A版 必修第二册
教材分析
教法学法
过程设计
课后反思
说课流程
(一)教材的地位及前后联系
向量是沟通代数、几何与三角函数的重要工具.
本节课是向量运算的起始课,为后继学习向量的其他运算以及空间向量奠定了基础.
本节内容在教材中占有极其重要的地位,在知识体系上起着承上启下的作用.
一、教材分析
1
知识目标
2
能力目标
3
情感目标
(二)教育教学目标
(三)教学重点难点
重点
两个向量的和的概念及其几何意义.
动手操作验证向量加法的运算律.
难点
学情分析:
物理学中位移和力等知识的学习,为学生学习本节课提供了知识背景.
二、教法学法设计
教学方法:
学习方法: 类比、迁移、分类、归纳.
教学手段:多媒体辅助教学.
启发-探究.
复习引入
作业推荐
法则探究
定义建构
运算律探究
学生总结
新知应用
三、教学过程设计
(一)复习引入
1.向量的概念及表示方法?
2.什么叫相等向量?
3.什么叫共线向量?
问题1 两个实数能进行加法运算,那么,
向量是否也能进行加法运算?
(二) 定义的建构
引例1 飞机从广州飞往上海,再从上海飞往北京(如图),这两次位移的结果与飞机从广州直接飞往北京的位移是否相同?
广州
上海
北京
(二) 定义的建构
引例2 求弹簧所受的拉力的合力
问题2 请结合“合位移”问题和“弹簧所受拉力的合力”问题,
试着给出向量加法的定义.
(三) 法则的探究
问题3 怎样求两个向量的和
A
a
b
B
C
a+b
a
b
三角形法则
(三) 法则的探究
A
b
B
C
a
b
平行四边形法则
a
a+b
(三) 法则的探究
2、方向相反
a
a
b
b
A
B
B
A
C
C
AC = a + b
AC = a + b
对于两个非零共线向量,能否通过两种加法法则求出他们的和?
a
b
1、方向相同
b
a
(三) 法则的探究
问题4 两种法则有何特征?
名称
运算结果
首尾关系
适用范围
向量
向量
首尾相连
任意非零向量
起点相同
不共线向量
角度
三角形法则
平行四边形法则
问题5 已知 是非零向量,则 与 之间
有什么关系?
结论 向量加法的三角形不等式
(三) 法则的探究
问题6 定义了一种新运算,自然要研究其运算律问题. 你
(四) 运算律的探究
类比旧知---猜想结论
动手操作---验证结论
能说出实数加法的运算律吗?向量的加法是否也
有运算律?有哪些运算律呢?
问题7 向量加法的交换律是否成立 请探究.
问题8 类比向量加法的交换律,向量加法的结合律是否
成立 请探究.
(四) 运算律的探究
向量加法的交换律
A
B
C
D
a
a
b
b
(四) 运算律的探究
向量加法的结合律
A
B
C
D
a
c
c
b
a
b
例2化简 (1) ; (2) ;
(3)
(五) 新知的初步应用
例1 如图,已知非零向量 ,求作向量 .
(1)
(2)
(五) 新知的初步应用
求有限个向量的和
(五) 新知的初步应用
例3 在长江南岸某渡口处,江水以12.5km/h的速 度向东流,渡船的速度为25km/h. 渡船要垂直的度过长江,其航向应如何确定.
(六)学生代表总结发言
(七) 分层次推荐作业
作业
思考题:
(1)向量的减法是如何定义的?其几何意义是什么?
(2)向量减法有哪些运算律?
(3)向量的减法与加法有何联系?
附: 板书设计
向量的加法运算
1.向量的加法定义
2.两个向量的和向量的作法
⑴平行四边形法则
⑵三角形法则
3.向量的运算律
例1
例2
引申
小结
作业
四、课后反思
通过创设问题情境, 层层设问的方式,“启发-探究”
注意讲练结合,做到教与学的有机结合.
采取小组总结发言, 提高学生的归纳、表达能力.
通过分层次推荐作业, 体现教学的巩固性和发展性原则.
的教学方法和“多媒体辅助教学”,让学生在探索中
获取和应用新知.
恳请批评指正!
谢谢!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
