河北省邢台市任泽区2023年九年级下册4月月考数学试卷(含答案)
文档属性
| 名称 | 河北省邢台市任泽区2023年九年级下册4月月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 153.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 16:32:13 | ||
图片预览




文档简介
2023年河北省邢台市任泽区中考数学月考试卷(4月份)
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 到的值是( )
A. B. C. D.
2. 下列命题中,真命题是( )
A. 两个锐角的和一定是钝角 B. 两点之间线段最短
C. 不是对顶角的两个角不相等 D. 带根号的数一定是无理数
3. 下列计算结果正确的是( )
A. B. C. D.
4. 下列说法正确的是( )
A. 平方根是 B. 的算术平方根是
C. 的算术平方根是 D. 的立方根是
5. 如图,下列条件能判断直线的有( )
;;;;
A. 个 B. 个 C. 个 D. 个
6. 若关于的方程有两个相等的实数根,则的值是( )
A. B. C. D.
7. 如图是某校七年级二班参加课外兴趣小组人数的扇形统计图,根据图中信息,你认为哪一个兴趣小组参加人数最多的是( )
A. 唱歌
B. 绘画
C. 编程
D. 舞蹈
8. 一元二次方程的根的情况是( )
A. 只有一个实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 没有实数根
9. 新冠病毒的直径约为纳米到纳米,在一次检测中检测人员把个新冠病毒排列在一起测得长度有米,则每一个新冠病毒的直径用科学记数法表示为多少米( )
A. B. C. D.
10. 下列图形属于中心对称的有( )
A. 个 B. 个 C. 个 D. 个
11. 如图,在平行四边形中,对角线,相交于,过点作交于若,,,则的长为( )
A. B.
C. D.
12. 一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )
A. B.
C. D.
13. 如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走米至坡顶处,再从处沿水平方向继续前行若干米到点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度根据以上数据,计算出建筑物的高度约为结果精确到参考数据:,,( )
A. 米 B. 米 C. 米 D. 米
14. 如图,在直角坐标系中,已知点,点为轴正半轴上一动点,连接,以为一边向下作等边三角形,连接,则的最小值为( )
A.
B.
C.
D.
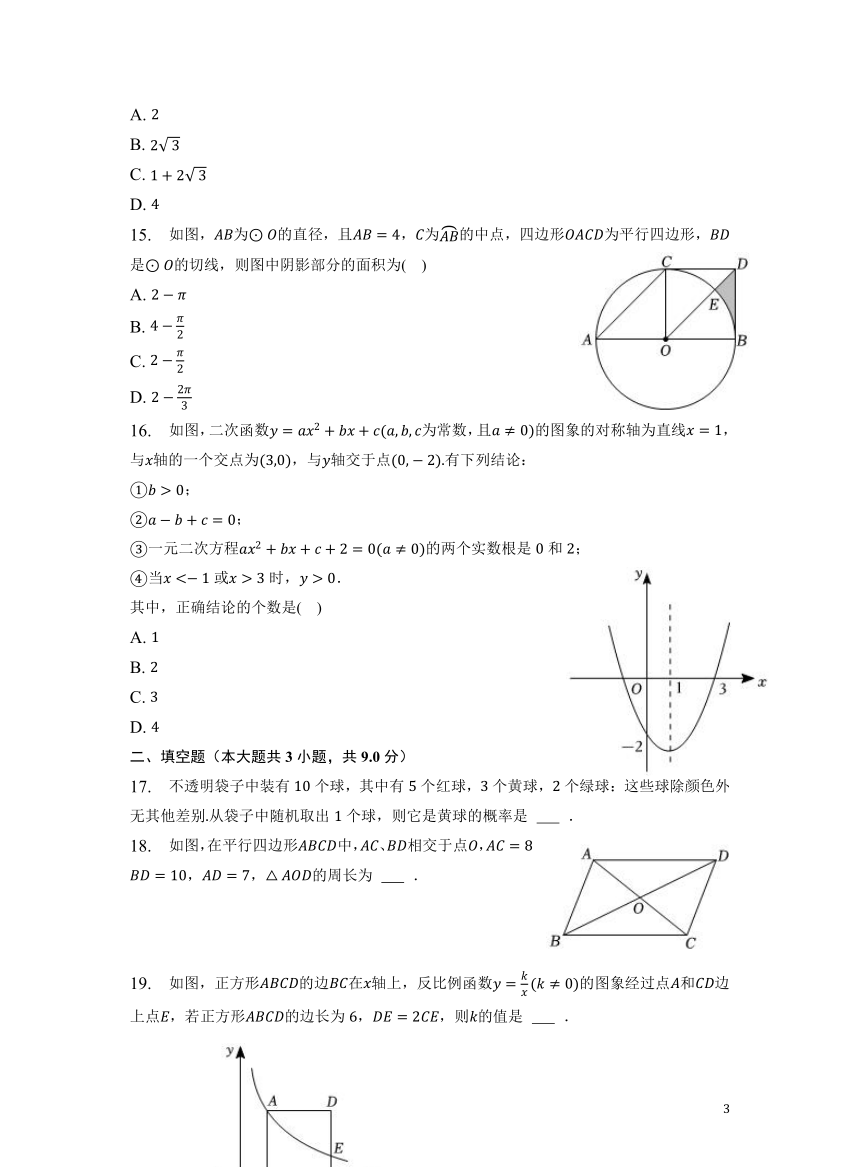
15. 如图,为的直径,且,为的中点,四边形为平行四边形,是的切线,则图中阴影部分的面积为( )
A.
B.
C.
D.
16. 如图,二次函数为常数,且的图象的对称轴为直线,与轴的一个交点为,与轴交于点有下列结论:
;
;
一元二次方程的两个实数根是和;
当或时,.
其中,正确结论的个数是( )
A.
B.
C.
D.
二、填空题(本大题共3小题,共9.0分)
17. 不透明袋子中装有个球,其中有个红球,个黄球,个绿球:这些球除颜色外无其他差别从袋子中随机取出个球,则它是黄球的概率是 .
18. 如图,在平行四边形中,、相交于点,,,,的周长为 .
19. 如图,正方形的边在轴上,反比例函数的图象经过点和边上点,若正方形的边长为,,则的值是 .
三、计算题(本大题共2小题,共9.0分)
20.(4.0分)计算:.
21.(5.0分)先化简,再求值:,其中.
四、解答题(本大题共6小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
22. 分我们知道,的几何意义是:在数轴上数对应的点到原点的距离,类似的,的几何意义就是:数轴上数,对应点之间的距离.比如:和两点之间的距离可以用表示,通过计算可以得到他们的距离是.
数轴上和两点之间的距离可以用______表示,通过计算可以得到他们的距离是______.
数轴上表示和的两点、之间的距离可以表示为______;如果,结合几何意义,那么的值为______;
代数式表示的几何意义是______,该代数式的最小值是______.
23. 分在“双减”政策背景下,越来越多的家长和孩子更加重观体育锻炼某兴趣小组为了解本校学生每天参加课外体育锻炼的情况,从全校学生中随机抽取了名学生进行问卷调查把每名学生平均每天参加课外体育锻炼的时间分成五个时间段进行统计,整理并绘制了如图两幅尚不完整的统计图根据上述信息,解答下列问题:
抽取的总人数 ,扇形统计图中“”对应扇形的圆心角的大小为 ,并请补全频数分布直方图.
本次调查学生每天的课外体育锻炼时间的中位数落在哪一组直接写出结果.
请估计该校名学生中,每天参加课外体育锻炼的时间不低于分钟的人数.
组别 体育锻炼时间分钟
24. 分如图,为的切线,为切点,过作的垂线,垂足为点交于点,延长与交于点,与的延长线交于点.
求证:为的切线;
若,求.
25. 分华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法甲、乙两人住同一小区,该小区到华山的距离为千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离千米与时间小时之间的函数关系;线段表示乙离开家的距离千米与时间小时之间的函数关系,点在线段上,请根据图象解答下列问题:
求点的坐标;
在整个过程中,求为何值时,甲、乙两人之间的距离恰好为千米.
26. 分已知:是等边三角形,点是包含边界平面内一点,连接,将线段绕逆时针旋转得到线段,连接,,,并延长交于点.
观察填空:当点在图所示的位置时,填空:
与全等的三角形是 .
的度数为 .
猜想证明:在图中,猜想线段,,之间有什么数量关系?直接写出答案.
拓展应用:如图,当边长为,时,请直接写出线段的最大值.
27. 分如图,平面直角坐标系中,抛物线交轴于,两点,交轴于点,点是线段上一个动点,过点作轴的垂线,交直线于点,交抛物线于点.
求抛物线的解析式;
当面积最大时,求点的坐标;
如图,是否存在以点、、为顶点的三角形与相似,若存在,求点的坐标;若不存在,请说明理由.
答案
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 12. 13. 14. 15.
16.
17. 18. 19.
20.解:
.
21.解:
,
当时,原式.
22. 或 数轴上表示数的点到和两点的距离的和
23.解:(1)由题意可得,m=3÷6%=50,
扇形统计图中“D”对应扇形的圆心角的大小为360°×20%=72°,
D组人数为:50×20%=10(人),B组人数为50-(3+18+10+8)=11(人),
补全频数分布直方图如下:
故答案为:50、72;
(2)∵一共50个数据,其中位数为第25、26个数据的平均数,而这2个数据均落在C组,
∴这组数据的中位数落在C组;
(3)3000×=2160(人),
答:估计每天参加课外体育锻炼的时间不低于40分钟的约有2160人.
24.证明:于点,
,
,
,
,
,
为的切线,为切点,
,
,
是的半径,且,
为的切线.
解:,
,
,
,
设,,,则,
,
,
,
,
,
,
,
将代入,得,
整理得,
.
25.解:设线段解析式为,
把,代入得:
,
解得,
线段解析式为,
令得,
的坐标为;
设线段解析式为,
把代入得:,
解得,
线段解析式为;
当乙未出发时,
在中,令,得,
乙出发后还未追上甲,
,
解得,
乙追上甲后,
,
解得,
综上所述,为或或时,甲、乙两人之间的距离恰好为千米.
26.解:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠ACB=∠ABC=∠BAC=60°,
∵线段CD绕C逆时针旋转60°得到线段CE,
∴∠DCE=60°,CD=CE,
∴∠ACD+∠DCB=∠BCE+∠DCB=60°,则∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
②∵△ACD≌△BCE,
∴∠DAC=∠EBC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠EBC+∠BAD=60°,
∴∠APB=180°-∠ABP-∠BAP=180°-∠ABC-∠EBC-∠BAP=180°-60°-60°=60°,
故答案为:①△BCE;②60°;
(2)结论:PD+PE=PC.
理由:由(1)②知,∠APB=∠ACB=60°,
则点A、B、C、D四点共圆,
∴∠APC=∠ABC=60°,
在PC上取一点F,使PF=PD,连接DF,则△PDF为等边三角形,
∴PD=DF,∠PDF=60°,
∵∠DCE=60°,CD=CE,
∴△CDE为等边三角形,
∴CD=DE,∠CDE=60°,
∴∠CDF=∠EDP,
在△CDF和△EDP中,
,
∴△CDF≌△EDP(SAS),
∴CF=PE,
∵PF+CF=PC,
∴PD+PE=PC;
(3)如图2,∵△ABC是等边三角形,
∴AC=4,
∴CD≤AC+AD=4+2=6,当且仅当点D在CA的延长线上时取等号,
∴CD的最大值为6,
又∵CD=CE,
∴CE的最大值为6.
27.解:抛物线过点,,,
代入得,,
解得,,
抛物线的解析式为:;
设,则,
设直线解析式为,
直线经过点,,
,
解得,
直线的解析式为,
,
,
,
当时,即当时,;
存在以点,,为顶点的三角形与相似,理由如下:
设,则,.
,
如图,过点作轴于点,则,
由可得:,,,
,
是等腰直角三角形,
当以点,,为顶点的三角形与相似时,与为对应顶点,
当∽时,,即,
解得:或舍去,
;
当∽时,,即,
解得:或舍去,
.
综上所述,或.
1
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
1. 到的值是( )
A. B. C. D.
2. 下列命题中,真命题是( )
A. 两个锐角的和一定是钝角 B. 两点之间线段最短
C. 不是对顶角的两个角不相等 D. 带根号的数一定是无理数
3. 下列计算结果正确的是( )
A. B. C. D.
4. 下列说法正确的是( )
A. 平方根是 B. 的算术平方根是
C. 的算术平方根是 D. 的立方根是
5. 如图,下列条件能判断直线的有( )
;;;;
A. 个 B. 个 C. 个 D. 个
6. 若关于的方程有两个相等的实数根,则的值是( )
A. B. C. D.
7. 如图是某校七年级二班参加课外兴趣小组人数的扇形统计图,根据图中信息,你认为哪一个兴趣小组参加人数最多的是( )
A. 唱歌
B. 绘画
C. 编程
D. 舞蹈
8. 一元二次方程的根的情况是( )
A. 只有一个实数根 B. 有两个相等的实数根
C. 有两个不相等的实数根 D. 没有实数根
9. 新冠病毒的直径约为纳米到纳米,在一次检测中检测人员把个新冠病毒排列在一起测得长度有米,则每一个新冠病毒的直径用科学记数法表示为多少米( )
A. B. C. D.
10. 下列图形属于中心对称的有( )
A. 个 B. 个 C. 个 D. 个
11. 如图,在平行四边形中,对角线,相交于,过点作交于若,,,则的长为( )
A. B.
C. D.
12. 一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )
A. B.
C. D.
13. 如图,为了测量某建筑物的高度,小颖采用了如下的方法:先从与建筑物底端在同一水平线上的点出发,沿斜坡行走米至坡顶处,再从处沿水平方向继续前行若干米到点处,在点测得该建筑物顶端的仰角为,建筑物底端的俯角为,点、、、、在同一平面内,斜坡的坡度根据以上数据,计算出建筑物的高度约为结果精确到参考数据:,,( )
A. 米 B. 米 C. 米 D. 米
14. 如图,在直角坐标系中,已知点,点为轴正半轴上一动点,连接,以为一边向下作等边三角形,连接,则的最小值为( )
A.
B.
C.
D.
15. 如图,为的直径,且,为的中点,四边形为平行四边形,是的切线,则图中阴影部分的面积为( )
A.
B.
C.
D.
16. 如图,二次函数为常数,且的图象的对称轴为直线,与轴的一个交点为,与轴交于点有下列结论:
;
;
一元二次方程的两个实数根是和;
当或时,.
其中,正确结论的个数是( )
A.
B.
C.
D.
二、填空题(本大题共3小题,共9.0分)
17. 不透明袋子中装有个球,其中有个红球,个黄球,个绿球:这些球除颜色外无其他差别从袋子中随机取出个球,则它是黄球的概率是 .
18. 如图,在平行四边形中,、相交于点,,,,的周长为 .
19. 如图,正方形的边在轴上,反比例函数的图象经过点和边上点,若正方形的边长为,,则的值是 .
三、计算题(本大题共2小题,共9.0分)
20.(4.0分)计算:.
21.(5.0分)先化简,再求值:,其中.
四、解答题(本大题共6小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
22. 分我们知道,的几何意义是:在数轴上数对应的点到原点的距离,类似的,的几何意义就是:数轴上数,对应点之间的距离.比如:和两点之间的距离可以用表示,通过计算可以得到他们的距离是.
数轴上和两点之间的距离可以用______表示,通过计算可以得到他们的距离是______.
数轴上表示和的两点、之间的距离可以表示为______;如果,结合几何意义,那么的值为______;
代数式表示的几何意义是______,该代数式的最小值是______.
23. 分在“双减”政策背景下,越来越多的家长和孩子更加重观体育锻炼某兴趣小组为了解本校学生每天参加课外体育锻炼的情况,从全校学生中随机抽取了名学生进行问卷调查把每名学生平均每天参加课外体育锻炼的时间分成五个时间段进行统计,整理并绘制了如图两幅尚不完整的统计图根据上述信息,解答下列问题:
抽取的总人数 ,扇形统计图中“”对应扇形的圆心角的大小为 ,并请补全频数分布直方图.
本次调查学生每天的课外体育锻炼时间的中位数落在哪一组直接写出结果.
请估计该校名学生中,每天参加课外体育锻炼的时间不低于分钟的人数.
组别 体育锻炼时间分钟
24. 分如图,为的切线,为切点,过作的垂线,垂足为点交于点,延长与交于点,与的延长线交于点.
求证:为的切线;
若,求.
25. 分华山古称“西岳”,为五岳之一,中华的“华”源于华山,因此华山有了“华夏之根”之称,华山南接秦岭山脉,北瞰黄渭,自古以来就有“奇险天下第一山”的说法甲、乙两人住同一小区,该小区到华山的距离为千米,两人先后从家出发沿同一路线驾车驶向华山,如图,线段表示甲离开家的距离千米与时间小时之间的函数关系;线段表示乙离开家的距离千米与时间小时之间的函数关系,点在线段上,请根据图象解答下列问题:
求点的坐标;
在整个过程中,求为何值时,甲、乙两人之间的距离恰好为千米.
26. 分已知:是等边三角形,点是包含边界平面内一点,连接,将线段绕逆时针旋转得到线段,连接,,,并延长交于点.
观察填空:当点在图所示的位置时,填空:
与全等的三角形是 .
的度数为 .
猜想证明:在图中,猜想线段,,之间有什么数量关系?直接写出答案.
拓展应用:如图,当边长为,时,请直接写出线段的最大值.
27. 分如图,平面直角坐标系中,抛物线交轴于,两点,交轴于点,点是线段上一个动点,过点作轴的垂线,交直线于点,交抛物线于点.
求抛物线的解析式;
当面积最大时,求点的坐标;
如图,是否存在以点、、为顶点的三角形与相似,若存在,求点的坐标;若不存在,请说明理由.
答案
1. 2. 3. 4. 5.
6. 7. 8. 9. 10.
11. 12. 13. 14. 15.
16.
17. 18. 19.
20.解:
.
21.解:
,
当时,原式.
22. 或 数轴上表示数的点到和两点的距离的和
23.解:(1)由题意可得,m=3÷6%=50,
扇形统计图中“D”对应扇形的圆心角的大小为360°×20%=72°,
D组人数为:50×20%=10(人),B组人数为50-(3+18+10+8)=11(人),
补全频数分布直方图如下:
故答案为:50、72;
(2)∵一共50个数据,其中位数为第25、26个数据的平均数,而这2个数据均落在C组,
∴这组数据的中位数落在C组;
(3)3000×=2160(人),
答:估计每天参加课外体育锻炼的时间不低于40分钟的约有2160人.
24.证明:于点,
,
,
,
,
,
为的切线,为切点,
,
,
是的半径,且,
为的切线.
解:,
,
,
,
设,,,则,
,
,
,
,
,
,
,
将代入,得,
整理得,
.
25.解:设线段解析式为,
把,代入得:
,
解得,
线段解析式为,
令得,
的坐标为;
设线段解析式为,
把代入得:,
解得,
线段解析式为;
当乙未出发时,
在中,令,得,
乙出发后还未追上甲,
,
解得,
乙追上甲后,
,
解得,
综上所述,为或或时,甲、乙两人之间的距离恰好为千米.
26.解:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠ACB=∠ABC=∠BAC=60°,
∵线段CD绕C逆时针旋转60°得到线段CE,
∴∠DCE=60°,CD=CE,
∴∠ACD+∠DCB=∠BCE+∠DCB=60°,则∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS);
②∵△ACD≌△BCE,
∴∠DAC=∠EBC,
∵∠DAC+∠BAD=∠BAC=60°,
∴∠EBC+∠BAD=60°,
∴∠APB=180°-∠ABP-∠BAP=180°-∠ABC-∠EBC-∠BAP=180°-60°-60°=60°,
故答案为:①△BCE;②60°;
(2)结论:PD+PE=PC.
理由:由(1)②知,∠APB=∠ACB=60°,
则点A、B、C、D四点共圆,
∴∠APC=∠ABC=60°,
在PC上取一点F,使PF=PD,连接DF,则△PDF为等边三角形,
∴PD=DF,∠PDF=60°,
∵∠DCE=60°,CD=CE,
∴△CDE为等边三角形,
∴CD=DE,∠CDE=60°,
∴∠CDF=∠EDP,
在△CDF和△EDP中,
,
∴△CDF≌△EDP(SAS),
∴CF=PE,
∵PF+CF=PC,
∴PD+PE=PC;
(3)如图2,∵△ABC是等边三角形,
∴AC=4,
∴CD≤AC+AD=4+2=6,当且仅当点D在CA的延长线上时取等号,
∴CD的最大值为6,
又∵CD=CE,
∴CE的最大值为6.
27.解:抛物线过点,,,
代入得,,
解得,,
抛物线的解析式为:;
设,则,
设直线解析式为,
直线经过点,,
,
解得,
直线的解析式为,
,
,
,
当时,即当时,;
存在以点,,为顶点的三角形与相似,理由如下:
设,则,.
,
如图,过点作轴于点,则,
由可得:,,,
,
是等腰直角三角形,
当以点,,为顶点的三角形与相似时,与为对应顶点,
当∽时,,即,
解得:或舍去,
;
当∽时,,即,
解得:或舍去,
.
综上所述,或.
1
同课章节目录
