湖北省天门市2022届九年级下学期期中学业质量检测数学试卷(含解析)
文档属性
| 名称 | 湖北省天门市2022届九年级下学期期中学业质量检测数学试卷(含解析) | 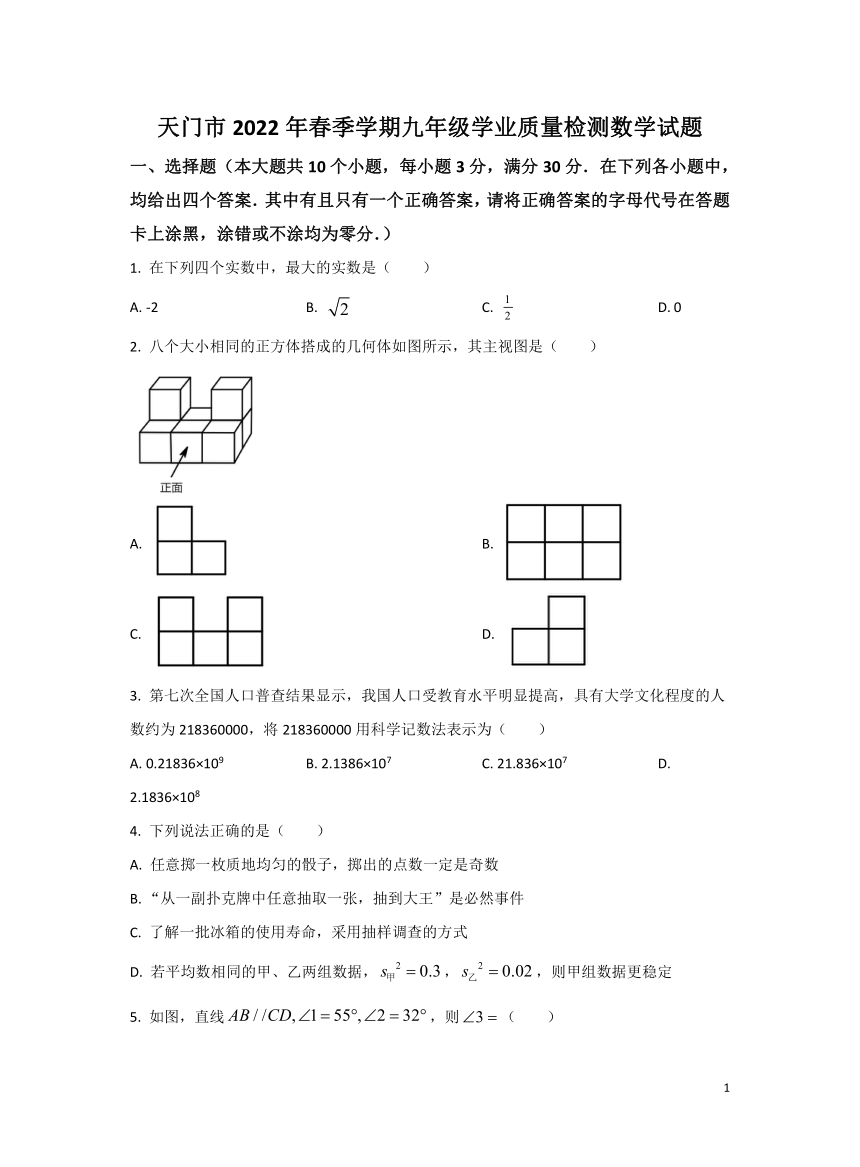 | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 17:10:40 | ||
图片预览




文档简介
天门市2022年春季学期九年级学业质量检测数学试题
一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案.其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)
1. 在下列四个实数中,最大的实数是( )
A. -2 B. C. D. 0
2. 八个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
3. 第七次全国人口普查结果显示,我国人口受教育水平明显提高,具有大学文化程度的人数约为218360000,将218360000用科学记数法表示为( )
A. 0.21836×109 B. 2.1386×107 C. 21.836×107 D. 2.1836×108
4. 下列说法正确的是( )
A. 任意掷一枚质地均匀的骰子,掷出的点数一定是奇数
B. “从一副扑克牌中任意抽取一张,抽到大王”是必然事件
C. 了解一批冰箱的使用寿命,采用抽样调查的方式
D. 若平均数相同的甲、乙两组数据,,,则甲组数据更稳定
5. 如图,直线,则( )
A. B. C. D.
6. 下列计算中,正确的是( )
A. B. C. D.
7. 若圆锥的侧面积为,底面半径为3.则该圆锥的母线长是( )
A 3 B. 4 C. 5 D. 6
8. 已知一次函数过点,则下列结论正确的是( )
A. y随x增大而增大 B.
C. 直线过点 D. 与坐标轴围成的三角形面积为2
9. 已知一元二次方程的两根为,,则的值为( )
A. B. C. 2 D. 5
10. 已知二次函数的图象交轴于两点.若其图象上有且只有三点满足,则的值是( )
A. 1 B. C. 2 D. 4
二.填空题(共5小题.每小题3分,满分15分)
11. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是_____.
12. 我国明代数学读本《算法统宗》有一道题,其题意:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两,银子共有_______两.(注:明代时1斤=16两)
13. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
14. 在桌面上放有四张背面完全一样的卡片.卡片的正面分别标有数字﹣1,0,1,3.把四张卡片背面朝上,随机抽取一张,记下数字且放回洗匀,再从中随机抽取一张.则两次抽取卡片上的数字之积为负数的概率是_______.
15. 如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为______.
三.解答题(共9小题,满分75分)
16. (1)先化简,再求值:,其中.
(2)解不等式组: .
17. 等腰中,,以为直径作圆交于点D,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画一条弦,使这条弦的长度等于弦.(保留作图痕迹,不写作法)
(1)如图1,;
(2)如图2,.
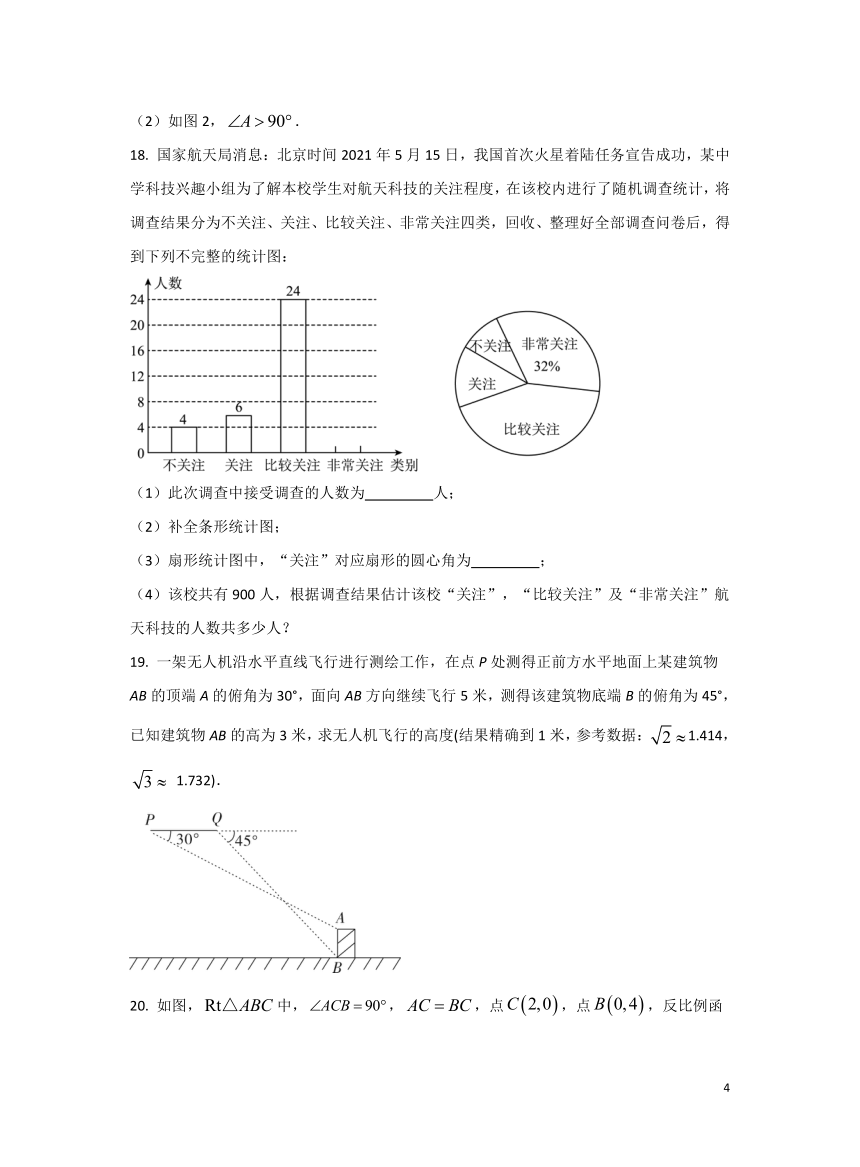
18. 国家航天局消息:北京时间2021年5月15日,我国首次火星着陆任务宣告成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图:
(1)此次调查中接受调查的人数为 人;
(2)补全条形统计图;
(3)扇形统计图中,“关注”对应扇形的圆心角为 ;
(4)该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?
19. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:1.414, 1.732).
20. 如图,中,,,点,点,反比例函数图象经过点A.
(1)求反比例函数的解析式;
(2)将直线向上平移个单位后经过反比例函数,图象上的点,求,的值.
21. 如图,是的外接圆,是的直径,于点.
(1)求证:;
(2)连接并延长,交于点,交于点,连接.若的半径为5,,求和的长.
22. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数(万人)与各自接种时间(天)之间的关系如图所示.
(1)直接写出乙地每天接种的人数及的值;
(2)当甲地接种速度放缓后,求关于的函数解析式,并写出自变量的取值范围;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
23. 在中,,,点在边上,,将线段绕点顺时针旋转至,记旋转角为,连接,,以为斜边在其一侧制作等腰直角三角形.连接.
(1)如图1,当时,请直接写出线段与线段的数量关系;
(2)当时,
①如图2,(1)中线段与线段的数量关系是否仍然成立?请说明理由;
②如图3,当,,三点共线时,连接,判断四边形的形状,并说明理由.
24. 如图,直线与x,y轴分别交于点B,A,顶点为P抛物线过点A.
(1)求出点A,B的坐标及c的值;
(2)若函数在时有最大值为,求a的值;
(3)若,连接AP,过点A作AP垂线交x轴于点M.设△BMP的面积为S.
①直接写出S关于a的函数关系式及a的取值范围;
②结合S与a的函数图象,直接写出时a的取值范围.
答案
1. B
解析:解:正数大于0,负数小于0,正数大于负数,
,
故选:B.
2. C
解析:解:由题意得该几何体的主视图为;
故选C.
3. D
解析:解:218360000=2.1836×108,
故选:D.
4. C
解析:解:.任意掷一枚质地均匀的骰子,掷出的点数不一定是奇数,故原说法错误,不合题意;
.“从一副扑克牌中任意抽取一张,抽到大王”是随机事件,故原说法错误,不合题意;
.了解一批冰箱的使用寿命,适合采用抽样调查的方式,说法正确,符合题意;
.若平均数相同的甲、乙两组数据,,,则乙组数据更稳定,故原说法错误,不合题意;
故选:.
5. A
解析:解:∵,
∴,
∴,
故选:A.
6. C
解析:解:2a+3a=5a,故选项A不符合题意;
a2 a3=a5,故选项B不符合题意;
2a 3a=6a2,故选项C符合题意;
(a2)3=a6,故选项D不符合题意;
故选:C.
7. D
解析:解:底面半径为3,圆锥的侧面积为,
设该圆锥的母线长是l,
由S=πrl可得18π=3πl.
解得:l=6,
故答案选:D.
8. C
解析:解:∵一次函数过点,
∴,解得,
∴一次函数为,y随x增大而减小,故A和B错误;
当时,,故C正确;
该一次函数与x轴交于点,与y轴交于点,
∴与坐标轴围成的三角形面积为,故D错误;
故选:C.
9. A
解析:解:∵一元二次方程的两根为,,
∴,即:,+=3,
∴=-2(+)=-1-2×3=-7.
故选A.
10. C
解析:解:假设点A在点B的左侧,
∵二次函数的图象交轴于两点,
∴令时,则有,解得:,
∴,
∴,
∵图象上有且只有三点满足,
∴点的纵坐标的绝对值相等,如图所示:
∵,
∴点,
∴;
故选C.
11. 720°##720度
解析:这个正多边形的边数为=6,
所以这个正多边形的内角和是(6﹣2)×180°=720°,
故答案为:720°.
12. 46
解析:解:设有人一起分银子,根据题意建立等式得,
,
解得:,
银子共有:(两)
故答案是:46.
13. 11
解析:解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
14. 解析:画树状图如图:
共有16个等可能的结果,两次抽取的卡片上的数字之积为负数的结果有4个,
∴两次抽取的卡片上的数字之积为负数的概率=.
故答案为:.
15. ①②④
解析:∵四边形ABCD为正方形,PD⊥DE,
∴∠PDA+∠PDC=90°,∠EDC+∠PDC=90°,AD=CD,
∴∠EDC=∠PDA,
在△APD和△CED中,
∴△APD≌△CED,故①正确,
∴∠APD=∠DEC,
∵DP=DE,∠PDE=90°,
∴∠DPE=∠DEP=45°,
∴∠APD=∠DEC=135°,
∴∠PEC=∠DEC-∠DEP=90°,
∴AE⊥CE,故②正确,
如图,过C作CF⊥DE,交DE的延长线于F,
∵,∠PDE=90°,
∴PE=,
∵,∠PEC=90°,
∴CE==2,
∵∠DEP=45°,∠PEC=90°,
∴∠FEC=45°,
∵∠EFC=90°,
∴△CEF是等腰直角三角形,
∴CF=EF==,
∴点到直线的距离为,故③错误,
∴DF=EF+DE=+1,
∴CD2===,
∴,故④正确,
综上所述:正确的结论有①②④,
故答案为:①②④
16. 解析:解∶(1)
当时,原式;
(2),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为.
17. (1)解:如图,为所作,
理由:连接,
∵为直径,
∴,
∵,
∴平分,即,
∴;
(2)解:如图,为所作,
理由:延长交圆于E,连接,同(1)可证,
∵,,
∴,
∵,
∴,
∴.
18. 解析:解:(1)不关注、关注、比较关注的共有4+6+24=34(人),占调查人数的1﹣32%=68%,
∴此次调查中接受调查的人数为34÷68%=50(人),
故答案为:50;
(2)50×32%=16(人),
补全统计图如图所示:
(3)360°43.2°,
故答案为:43.2°;
(4)900828(人),
答:估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共有828人.
19.解:如图,延长PQ,BA,相交于点E,
由题意可得:AB⊥PQ,∠E=90°,
又∵∠BQE=45°,
∴BE=QE,
设BE=QE=x,
∵PQ=5,AB=3,
∴PE=x+5,AE=x-3,
∵∠E=90°,
∴sin∠APE=,
∵∠APE=30°,
∴sin30°=,
解得:x=≈14,
答:无人机飞行的高度约为14米.
20. 解析:(1)如图,作轴,则
,,
点,点
,
∴OD=OC+CD=6,
代入中,
.
(2)在上,
设直线OA解析式为
,
直线向上平移个单位后的解析式为:
图象经过(1,12)
解得:
,.
21. 解析:(1)证明:∵是的直径,,
∴,
∴;
(2)解:由题意可得如图所示:
由(1)可得点E为BC的中点,
∵点O是BG的中点,
∴,
∴,
∴,
∵,
∴,
∵的半径为5,
∴,
∴,
∴.
22. 解析:解:(1)乙地接种速度为(万人/天),
,
解得.
(2)设,将,代入解析式得:
,
解得,
∴.
(3)把代入得,
(万人).
23. 解析:(1)如图1,
,,
,
是以为斜边等腰直角三角形,
,,
,
,
,
,
,
即;
(2)①仍然成立,理由如下:
如图2,
,,
,
是以为斜边等腰直角三角形,
,,
,
,
即,
,
,
,
,
,
即;
②四边形是平行四边形,理由如下:
如图3,过作,连接, 交于点,
,,
,
,
,
,
是以为斜边等腰直角三角形,
,
,,三点共线,
,
,
,
,
,
,
,
,
,
,
,
,
由①可知,
,
是以为斜边等腰直角三角形,
,,
,
,
,
,
,
,
即,
,
,
,
四边形是平行四边形.
24. 解析:解:(1)∵直线与x,y轴分别交于点B,A,
∴点A(0,1),点B(-2,0),
∵抛物线过点A,
∴;
(2)∵,
∴对称轴为直线,
当,时,y随x的增大而增大
∴当时,y有最大值,
∴,
解得:;
当,时,y随x增大而减小,
∴当时,y有最大值,
∴,
解得:(不合题意舍去),
综上所述:
(3)①当,时,即,
如图2,过点P作轴于N,
∴,,
同理可得,
∴,
∴,
∴;
当,时,即,
如图3,过点P作轴于N,
∴,,,
同理可得,
∴,
∴,
∴;
当时,点B与点M重合,不合题意,
当,时,即,
如图4,过点P作轴于N,
∴,,,
同理可得,
∴,
∴,
∴;
综上所述:
②当时,,
∴当时,不存在a的值使;
当时,开口向上,对称轴为直线,S随a的增大而减小
当时,解得
∴;
当时,开口向上,对称轴为直线,S随a的增大而增大,
∴,
综上所述:或
1
一、选择题(本大题共10个小题,每小题3分,满分30分.在下列各小题中,均给出四个答案.其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.)
1. 在下列四个实数中,最大的实数是( )
A. -2 B. C. D. 0
2. 八个大小相同的正方体搭成的几何体如图所示,其主视图是( )
A. B.
C. D.
3. 第七次全国人口普查结果显示,我国人口受教育水平明显提高,具有大学文化程度的人数约为218360000,将218360000用科学记数法表示为( )
A. 0.21836×109 B. 2.1386×107 C. 21.836×107 D. 2.1836×108
4. 下列说法正确的是( )
A. 任意掷一枚质地均匀的骰子,掷出的点数一定是奇数
B. “从一副扑克牌中任意抽取一张,抽到大王”是必然事件
C. 了解一批冰箱的使用寿命,采用抽样调查的方式
D. 若平均数相同的甲、乙两组数据,,,则甲组数据更稳定
5. 如图,直线,则( )
A. B. C. D.
6. 下列计算中,正确的是( )
A. B. C. D.
7. 若圆锥的侧面积为,底面半径为3.则该圆锥的母线长是( )
A 3 B. 4 C. 5 D. 6
8. 已知一次函数过点,则下列结论正确的是( )
A. y随x增大而增大 B.
C. 直线过点 D. 与坐标轴围成的三角形面积为2
9. 已知一元二次方程的两根为,,则的值为( )
A. B. C. 2 D. 5
10. 已知二次函数的图象交轴于两点.若其图象上有且只有三点满足,则的值是( )
A. 1 B. C. 2 D. 4
二.填空题(共5小题.每小题3分,满分15分)
11. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是_____.
12. 我国明代数学读本《算法统宗》有一道题,其题意:客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两,银子共有_______两.(注:明代时1斤=16两)
13. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
14. 在桌面上放有四张背面完全一样的卡片.卡片的正面分别标有数字﹣1,0,1,3.把四张卡片背面朝上,随机抽取一张,记下数字且放回洗匀,再从中随机抽取一张.则两次抽取卡片上的数字之积为负数的概率是_______.
15. 如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为______.
三.解答题(共9小题,满分75分)
16. (1)先化简,再求值:,其中.
(2)解不等式组: .
17. 等腰中,,以为直径作圆交于点D,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画一条弦,使这条弦的长度等于弦.(保留作图痕迹,不写作法)
(1)如图1,;
(2)如图2,.
18. 国家航天局消息:北京时间2021年5月15日,我国首次火星着陆任务宣告成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图:
(1)此次调查中接受调查的人数为 人;
(2)补全条形统计图;
(3)扇形统计图中,“关注”对应扇形的圆心角为 ;
(4)该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?
19. 一架无人机沿水平直线飞行进行测绘工作,在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B的俯角为45°,已知建筑物AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:1.414, 1.732).
20. 如图,中,,,点,点,反比例函数图象经过点A.
(1)求反比例函数的解析式;
(2)将直线向上平移个单位后经过反比例函数,图象上的点,求,的值.
21. 如图,是的外接圆,是的直径,于点.
(1)求证:;
(2)连接并延长,交于点,交于点,连接.若的半径为5,,求和的长.
22. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数(万人)与各自接种时间(天)之间的关系如图所示.
(1)直接写出乙地每天接种的人数及的值;
(2)当甲地接种速度放缓后,求关于的函数解析式,并写出自变量的取值范围;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
23. 在中,,,点在边上,,将线段绕点顺时针旋转至,记旋转角为,连接,,以为斜边在其一侧制作等腰直角三角形.连接.
(1)如图1,当时,请直接写出线段与线段的数量关系;
(2)当时,
①如图2,(1)中线段与线段的数量关系是否仍然成立?请说明理由;
②如图3,当,,三点共线时,连接,判断四边形的形状,并说明理由.
24. 如图,直线与x,y轴分别交于点B,A,顶点为P抛物线过点A.
(1)求出点A,B的坐标及c的值;
(2)若函数在时有最大值为,求a的值;
(3)若,连接AP,过点A作AP垂线交x轴于点M.设△BMP的面积为S.
①直接写出S关于a的函数关系式及a的取值范围;
②结合S与a的函数图象,直接写出时a的取值范围.
答案
1. B
解析:解:正数大于0,负数小于0,正数大于负数,
,
故选:B.
2. C
解析:解:由题意得该几何体的主视图为;
故选C.
3. D
解析:解:218360000=2.1836×108,
故选:D.
4. C
解析:解:.任意掷一枚质地均匀的骰子,掷出的点数不一定是奇数,故原说法错误,不合题意;
.“从一副扑克牌中任意抽取一张,抽到大王”是随机事件,故原说法错误,不合题意;
.了解一批冰箱的使用寿命,适合采用抽样调查的方式,说法正确,符合题意;
.若平均数相同的甲、乙两组数据,,,则乙组数据更稳定,故原说法错误,不合题意;
故选:.
5. A
解析:解:∵,
∴,
∴,
故选:A.
6. C
解析:解:2a+3a=5a,故选项A不符合题意;
a2 a3=a5,故选项B不符合题意;
2a 3a=6a2,故选项C符合题意;
(a2)3=a6,故选项D不符合题意;
故选:C.
7. D
解析:解:底面半径为3,圆锥的侧面积为,
设该圆锥的母线长是l,
由S=πrl可得18π=3πl.
解得:l=6,
故答案选:D.
8. C
解析:解:∵一次函数过点,
∴,解得,
∴一次函数为,y随x增大而减小,故A和B错误;
当时,,故C正确;
该一次函数与x轴交于点,与y轴交于点,
∴与坐标轴围成的三角形面积为,故D错误;
故选:C.
9. A
解析:解:∵一元二次方程的两根为,,
∴,即:,+=3,
∴=-2(+)=-1-2×3=-7.
故选A.
10. C
解析:解:假设点A在点B的左侧,
∵二次函数的图象交轴于两点,
∴令时,则有,解得:,
∴,
∴,
∵图象上有且只有三点满足,
∴点的纵坐标的绝对值相等,如图所示:
∵,
∴点,
∴;
故选C.
11. 720°##720度
解析:这个正多边形的边数为=6,
所以这个正多边形的内角和是(6﹣2)×180°=720°,
故答案为:720°.
12. 46
解析:解:设有人一起分银子,根据题意建立等式得,
,
解得:,
银子共有:(两)
故答案是:46.
13. 11
解析:解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
14. 解析:画树状图如图:
共有16个等可能的结果,两次抽取的卡片上的数字之积为负数的结果有4个,
∴两次抽取的卡片上的数字之积为负数的概率=.
故答案为:.
15. ①②④
解析:∵四边形ABCD为正方形,PD⊥DE,
∴∠PDA+∠PDC=90°,∠EDC+∠PDC=90°,AD=CD,
∴∠EDC=∠PDA,
在△APD和△CED中,
∴△APD≌△CED,故①正确,
∴∠APD=∠DEC,
∵DP=DE,∠PDE=90°,
∴∠DPE=∠DEP=45°,
∴∠APD=∠DEC=135°,
∴∠PEC=∠DEC-∠DEP=90°,
∴AE⊥CE,故②正确,
如图,过C作CF⊥DE,交DE的延长线于F,
∵,∠PDE=90°,
∴PE=,
∵,∠PEC=90°,
∴CE==2,
∵∠DEP=45°,∠PEC=90°,
∴∠FEC=45°,
∵∠EFC=90°,
∴△CEF是等腰直角三角形,
∴CF=EF==,
∴点到直线的距离为,故③错误,
∴DF=EF+DE=+1,
∴CD2===,
∴,故④正确,
综上所述:正确的结论有①②④,
故答案为:①②④
16. 解析:解∶(1)
当时,原式;
(2),
解不等式①得:,
解不等式②得:,
∴不等式组的解集为.
17. (1)解:如图,为所作,
理由:连接,
∵为直径,
∴,
∵,
∴平分,即,
∴;
(2)解:如图,为所作,
理由:延长交圆于E,连接,同(1)可证,
∵,,
∴,
∵,
∴,
∴.
18. 解析:解:(1)不关注、关注、比较关注的共有4+6+24=34(人),占调查人数的1﹣32%=68%,
∴此次调查中接受调查的人数为34÷68%=50(人),
故答案为:50;
(2)50×32%=16(人),
补全统计图如图所示:
(3)360°43.2°,
故答案为:43.2°;
(4)900828(人),
答:估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共有828人.
19.解:如图,延长PQ,BA,相交于点E,
由题意可得:AB⊥PQ,∠E=90°,
又∵∠BQE=45°,
∴BE=QE,
设BE=QE=x,
∵PQ=5,AB=3,
∴PE=x+5,AE=x-3,
∵∠E=90°,
∴sin∠APE=,
∵∠APE=30°,
∴sin30°=,
解得:x=≈14,
答:无人机飞行的高度约为14米.
20. 解析:(1)如图,作轴,则
,,
点,点
,
∴OD=OC+CD=6,
代入中,
.
(2)在上,
设直线OA解析式为
,
直线向上平移个单位后的解析式为:
图象经过(1,12)
解得:
,.
21. 解析:(1)证明:∵是的直径,,
∴,
∴;
(2)解:由题意可得如图所示:
由(1)可得点E为BC的中点,
∵点O是BG的中点,
∴,
∴,
∴,
∵,
∴,
∵的半径为5,
∴,
∴,
∴.
22. 解析:解:(1)乙地接种速度为(万人/天),
,
解得.
(2)设,将,代入解析式得:
,
解得,
∴.
(3)把代入得,
(万人).
23. 解析:(1)如图1,
,,
,
是以为斜边等腰直角三角形,
,,
,
,
,
,
,
即;
(2)①仍然成立,理由如下:
如图2,
,,
,
是以为斜边等腰直角三角形,
,,
,
,
即,
,
,
,
,
,
即;
②四边形是平行四边形,理由如下:
如图3,过作,连接, 交于点,
,,
,
,
,
,
是以为斜边等腰直角三角形,
,
,,三点共线,
,
,
,
,
,
,
,
,
,
,
,
,
由①可知,
,
是以为斜边等腰直角三角形,
,,
,
,
,
,
,
,
即,
,
,
,
四边形是平行四边形.
24. 解析:解:(1)∵直线与x,y轴分别交于点B,A,
∴点A(0,1),点B(-2,0),
∵抛物线过点A,
∴;
(2)∵,
∴对称轴为直线,
当,时,y随x的增大而增大
∴当时,y有最大值,
∴,
解得:;
当,时,y随x增大而减小,
∴当时,y有最大值,
∴,
解得:(不合题意舍去),
综上所述:
(3)①当,时,即,
如图2,过点P作轴于N,
∴,,
同理可得,
∴,
∴,
∴;
当,时,即,
如图3,过点P作轴于N,
∴,,,
同理可得,
∴,
∴,
∴;
当时,点B与点M重合,不合题意,
当,时,即,
如图4,过点P作轴于N,
∴,,,
同理可得,
∴,
∴,
∴;
综上所述:
②当时,,
∴当时,不存在a的值使;
当时,开口向上,对称轴为直线,S随a的增大而减小
当时,解得
∴;
当时,开口向上,对称轴为直线,S随a的增大而增大,
∴,
综上所述:或
1
同课章节目录
