5.1圆 课件(共25张PPT)- 鲁教版数学九年级下册
文档属性
| 名称 | 5.1圆 课件(共25张PPT)- 鲁教版数学九年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 18:22:45 | ||
图片预览








文档简介
(共25张PPT)
5.1 圆
第五章 圆
知识点
感悟新知
1
圆
1. 圆的定义
(1)描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周, 另一个端点A 所形成的图形叫做圆.其固定的端点O 叫做圆心,线段OA 叫做半径.
感悟新知
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
感悟新知
(2)集合观点定义:圆可以看成是所有到定点(圆心O)的距离等于定长(半径r)的点的集合.
2. 圆的表示法 以点O 为圆心的圆,记作⊙ O,读作“圆O”.
3. 圆的特性 (1)同圆的半径相等.
(2)到圆心的距离等于半径的点在圆上.
感悟新知
下列说法中,错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例 1
A
感悟新知
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,圆心和半径都确定,这样的圆有且只有一个(唯一).
感悟新知
1-1. 下列条件中,能确定唯一一个圆的是( )
A. 以点O 为圆心
B. 以2 cm 长为半径
C. 以点O 为圆心,5 cm长为半径
D. 半径为2 cm 且经过点A
C
感悟新知
1-2. 到点O 的距离等于8 cm 的点的集合是以点________为圆心,以________ cm长为半径的圆.
O
8
感悟新知
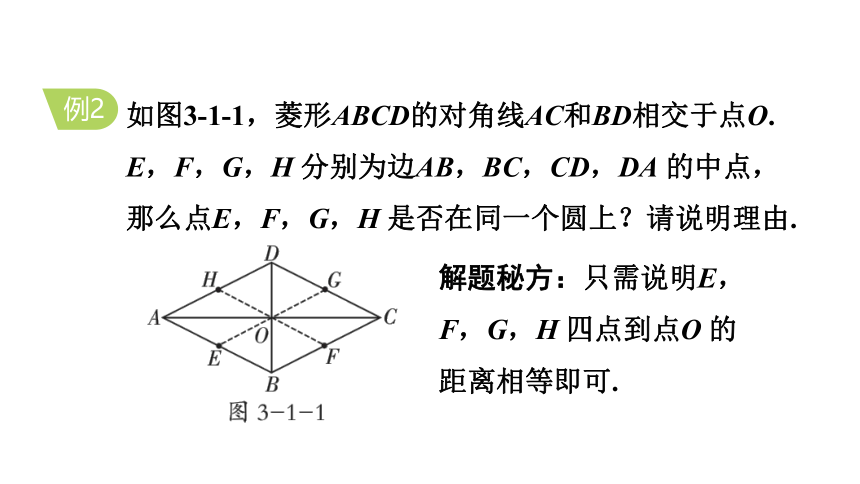
如图3-1-1,菱形ABCD的对角线AC和BD相交于点O.
E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例2
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等即可.
感悟新知
解:点E,F,G,H 在同一个圆上,理由如下:
如图3-1-1,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,AC ⊥ BD.
感悟新知
又∵ E 为AB 边的中点,
∴ OE= AB.
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
感悟新知
2-1. 如图,BD,CE是△ ABC 的高,M 是BC 的中点,试说明点B,C,D,E 在以点M 为圆心的同一个圆上.
感悟新知
知识点
圆的有关概念
感悟新知
2
定义 注意
弦 连接圆上任意两点的线段叫做弦 圆中有无数条弦,其中直径经过圆心的弦叫做直径直径是最长的弦
直径 经过圆心的弦叫做直径
感悟新知
弧、半圆、劣弧、优弧、 (1)圆上任意两点间的部分叫做圆弧,简称弧;
(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;
(3)小于半圆的弧叫做劣弧;
(4)大于半圆的弧叫做优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
感悟新知
等圆 能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 在同圆或等圆中,能够互相重合的弧叫做等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
前提
感悟新知
1.弦与直径的关系:直径是圆中最长的弦,但弦不一定是直径.
2.弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦和弧都有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条.
感悟新知
下列语句中:①直径是弦;②弦是直径;③半径相等
的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有 ____________.
①③⑤
例 3
感悟新知
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半径相等的两个半圆能互相重合,所以是等弧,故③正确;在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
感悟新知
3-1. 如图,在⊙ O 中,点A,O,D 在一条直线上, 点B,O,C 在一条直线上,那么图中有________条弦.
3
知识点
点和圆的位置关系
感悟新知
3
点和圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等级关系
点在圆外 点到圆心的距离大于半径 点P 在圆外d > r
点在圆上 点到圆心的距离等于半径 点P 在圆上d=r
点在圆内 点到圆心的距离小于半径 点P 在圆内d < r
感悟新知
如图3-1-2,已知⊙ O 的半径r=5 cm,圆心O 到直
线l 的距离d=OD=3 cm,在直线l 上有P,Q,R 三点,且有PD=4 cm,QD=5 cm,RD=
3 cm,那么P,Q,R 三点与⊙
O 的位置关系各是怎样的?
例4
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
感悟新知
解:如图3-1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP=5 cm=r. ∴点P 在⊙ O 上.
∵ QD=5 cm,∴ OQ= cm>5 cm,∴点Q 在⊙ O 外.
∵ RD=3 cm,∴ OR=3 cm<5 cm. ∴点R 在⊙ O 内.
感悟新知
4-1. 在矩形ABCD 中,AB=8,AD=6,以顶点D 为圆心作半径为r 的圆,若要求另外三个顶点A,B,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是 ________.
6课堂小结
圆
圆
弦、弧、等圆、等弧
两要素
位置
大小
圆心
半径
相关概念
点与圆的位置关系
点在圆上、圆内、圆外
5.1 圆
第五章 圆
知识点
感悟新知
1
圆
1. 圆的定义
(1)描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周, 另一个端点A 所形成的图形叫做圆.其固定的端点O 叫做圆心,线段OA 叫做半径.
感悟新知
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3. “圆上的点”指圆周上的点.
感悟新知
(2)集合观点定义:圆可以看成是所有到定点(圆心O)的距离等于定长(半径r)的点的集合.
2. 圆的表示法 以点O 为圆心的圆,记作⊙ O,读作“圆O”.
3. 圆的特性 (1)同圆的半径相等.
(2)到圆心的距离等于半径的点在圆上.
感悟新知
下列说法中,错误的有( )
(1)经过点P 的圆有无数个;
(2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
例 1
A
感悟新知
解:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,圆心和半径都确定,这样的圆有且只有一个(唯一).
感悟新知
1-1. 下列条件中,能确定唯一一个圆的是( )
A. 以点O 为圆心
B. 以2 cm 长为半径
C. 以点O 为圆心,5 cm长为半径
D. 半径为2 cm 且经过点A
C
感悟新知
1-2. 到点O 的距离等于8 cm 的点的集合是以点________为圆心,以________ cm长为半径的圆.
O
8
感悟新知
如图3-1-1,菱形ABCD的对角线AC和BD相交于点O.
E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
例2
解题秘方:只需说明E,F,G,H 四点到点O 的距离相等即可.
感悟新知
解:点E,F,G,H 在同一个圆上,理由如下:
如图3-1-1,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,
∴ AB=BC=CD=DA,AC ⊥ BD.
感悟新知
又∵ E 为AB 边的中点,
∴ OE= AB.
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
感悟新知
2-1. 如图,BD,CE是△ ABC 的高,M 是BC 的中点,试说明点B,C,D,E 在以点M 为圆心的同一个圆上.
感悟新知
知识点
圆的有关概念
感悟新知
2
定义 注意
弦 连接圆上任意两点的线段叫做弦 圆中有无数条弦,其中直径经过圆心的弦叫做直径直径是最长的弦
直径 经过圆心的弦叫做直径
感悟新知
弧、半圆、劣弧、优弧、 (1)圆上任意两点间的部分叫做圆弧,简称弧;
(2)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆;
(3)小于半圆的弧叫做劣弧;
(4)大于半圆的弧叫做优弧 弧包括优弧、劣弧和半圆;半圆既不是劣弧,也不是优弧
感悟新知
等圆 能够重合的两个圆叫做等圆. 容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等 等圆只和半径的大小有关,和圆心的位置无关
等弧 在同圆或等圆中,能够互相重合的弧叫做等弧 等弧只能出现在同圆或等圆中;等弧是全等的,而不仅仅是弧的长度相等
前提
感悟新知
1.弦与直径的关系:直径是圆中最长的弦,但弦不一定是直径.
2.弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦和弧都有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条.
感悟新知
下列语句中:①直径是弦;②弦是直径;③半径相等
的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有 ____________.
①③⑤
例 3
感悟新知
解:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半径相等的两个半圆能互相重合,所以是等弧,故③正确;在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
感悟新知
3-1. 如图,在⊙ O 中,点A,O,D 在一条直线上, 点B,O,C 在一条直线上,那么图中有________条弦.
3
知识点
点和圆的位置关系
感悟新知
3
点和圆的位置关系
设⊙ O 的半径为r,点P 到圆心的距离OP=d,则有:
点和圆的位置关系 特点 等级关系
点在圆外 点到圆心的距离大于半径 点P 在圆外d > r
点在圆上 点到圆心的距离等于半径 点P 在圆上d=r
点在圆内 点到圆心的距离小于半径 点P 在圆内d < r
感悟新知
如图3-1-2,已知⊙ O 的半径r=5 cm,圆心O 到直
线l 的距离d=OD=3 cm,在直线l 上有P,Q,R 三点,且有PD=4 cm,QD=5 cm,RD=
3 cm,那么P,Q,R 三点与⊙
O 的位置关系各是怎样的?
例4
解题秘方:比较点到圆心的距离与半径的大小确定点的位置情况.
感悟新知
解:如图3-1-2,连接OR,OP,OQ.
∵ PD=4 cm,OD=3 cm,且OD ⊥ l,
∴ OP=5 cm=r. ∴点P 在⊙ O 上.
∵ QD=5 cm,∴ OQ= cm>5 cm,∴点Q 在⊙ O 外.
∵ RD=3 cm,∴ OR=3 cm<5 cm. ∴点R 在⊙ O 内.
感悟新知
4-1. 在矩形ABCD 中,AB=8,AD=6,以顶点D 为圆心作半径为r 的圆,若要求另外三个顶点A,B,C 中至少有一个点在圆内,且至少有一个点在圆外,则r 的取值范围是 ________.
6
圆
圆
弦、弧、等圆、等弧
两要素
位置
大小
圆心
半径
相关概念
点与圆的位置关系
点在圆上、圆内、圆外
