11.1.2三角形的高、中线和角平分线
文档属性
| 名称 | 11.1.2三角形的高、中线和角平分线 | 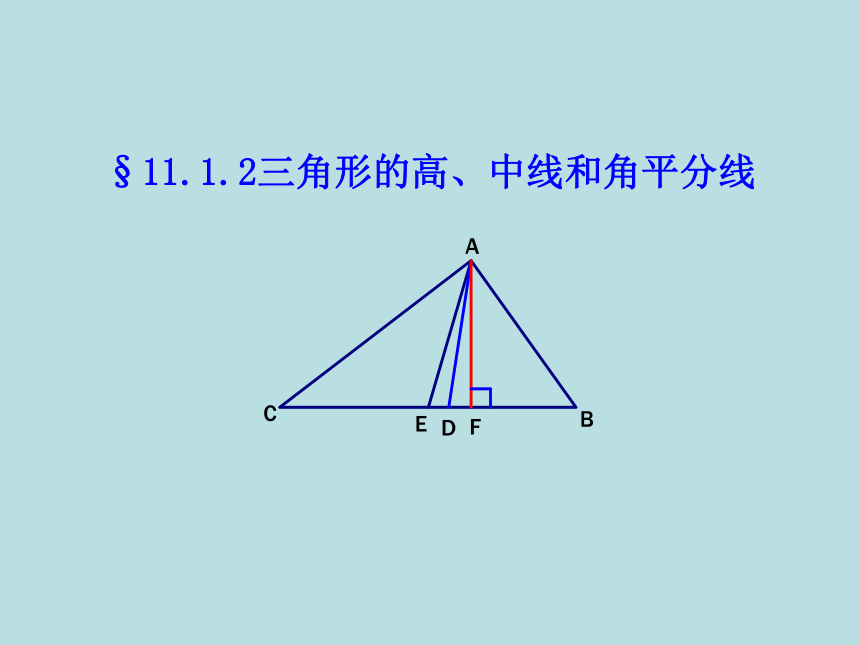 | |
| 格式 | zip | ||
| 文件大小 | 922.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-30 09:03:46 | ||
图片预览




文档简介
课件32张PPT。§11.1.2三角形的高、中线和角平分线 1.理解三角形的高、中线和角平分线的含义,并会作出这三种重要的线段.
2.了解三角形的高、中线、和角平分线的性质,并能应用它解决一些问题.
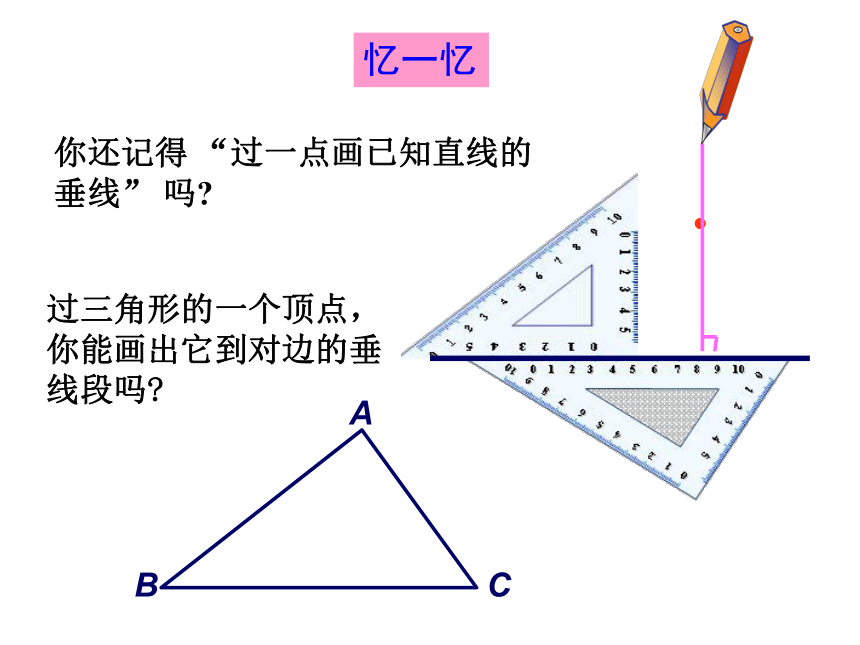
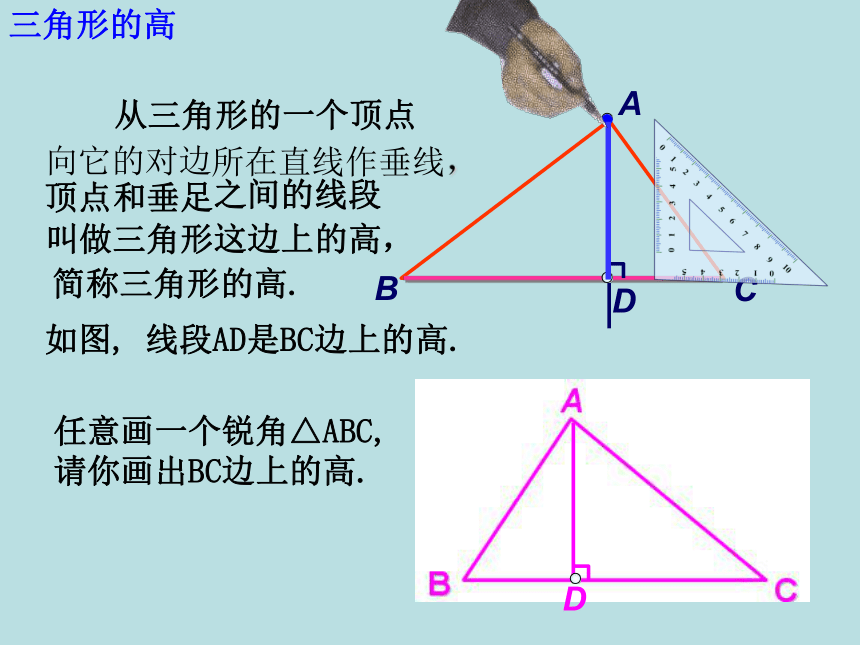
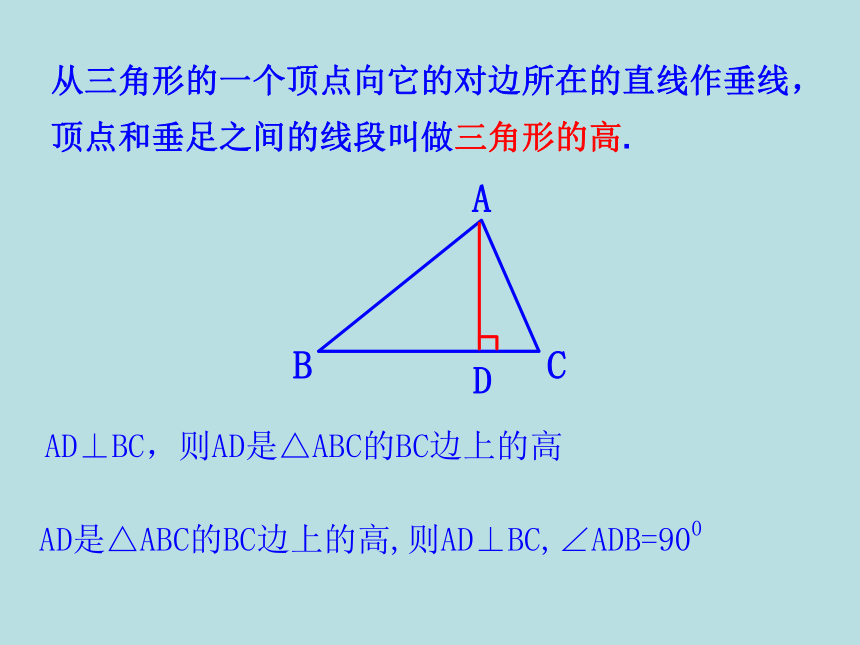
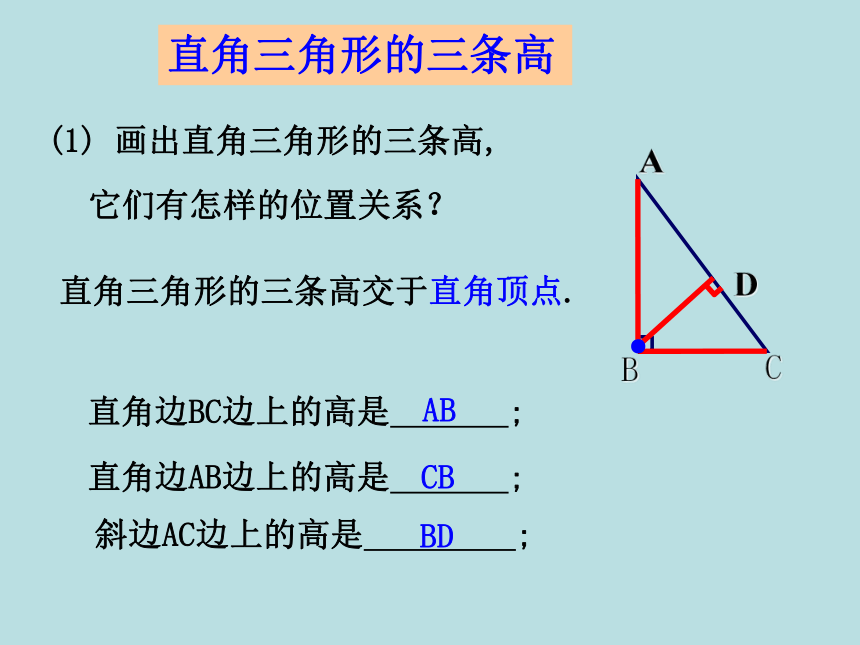
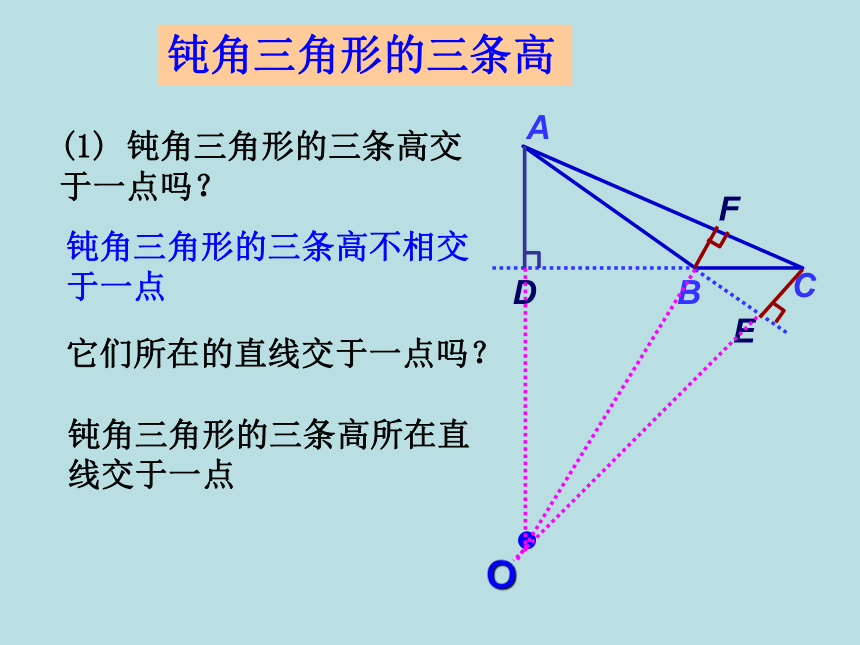
3.感受数学知识的广泛用途和科学探究精神.2.线段中点的定义:3.角平分线的定义:1.垂线的定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.把一条线段分成两条相等的线段的点.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.忆一忆你还记得 “过一点画已知直线的垂线” 吗?过三角形的一个顶点,你能画出它到对边的垂线段吗?忆一忆A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角△ABC,请你画出BC边上的高.三角形的高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高.AD⊥BC,则AD是△ABC的BC边上的高AD是△ABC的BC边上的高,则AD⊥BC,∠ADB=900(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?锐角三角形的三条高交于同一点.(3)锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部.ABCDEF锐角三角形的三条高ABC(1) 画出直角三角形的三条高,直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 ;BD●直角三角形的三条高(1) 钝角三角形的三条高交于一点吗?钝角三角形的三条高不相交于一点它们所在的直线交于一点吗?钝角三角形的三条高所在直线交于一点O钝角三角形的三条高333都在三角
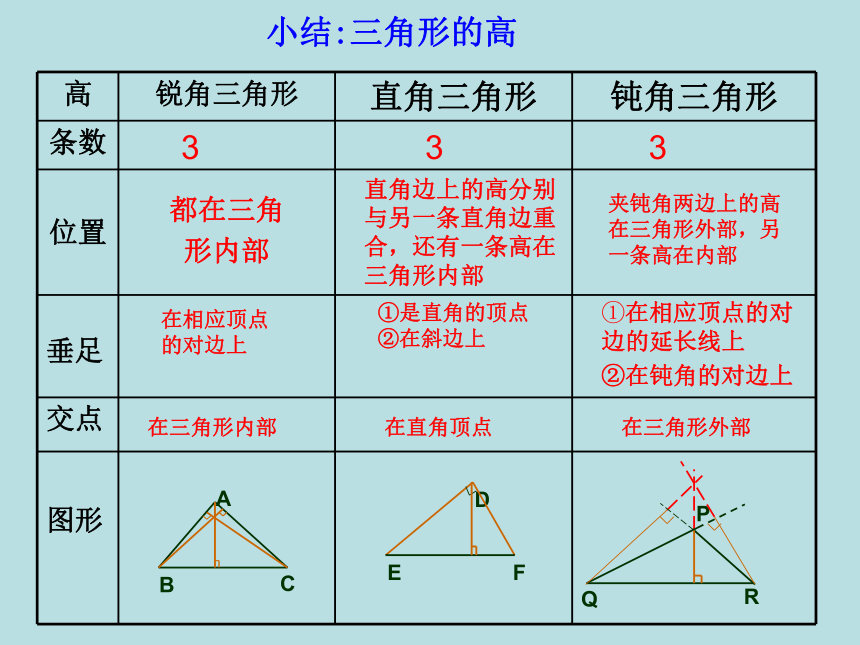
形内部直角边上的高分别与另一条直角边重合,还有一条高在三角形内部夹钝角两边上的高在三角形外部,另一条高在内部在相应顶点的对边上①是直角的顶点
②在斜边上①在相应顶点的对边的延长线上
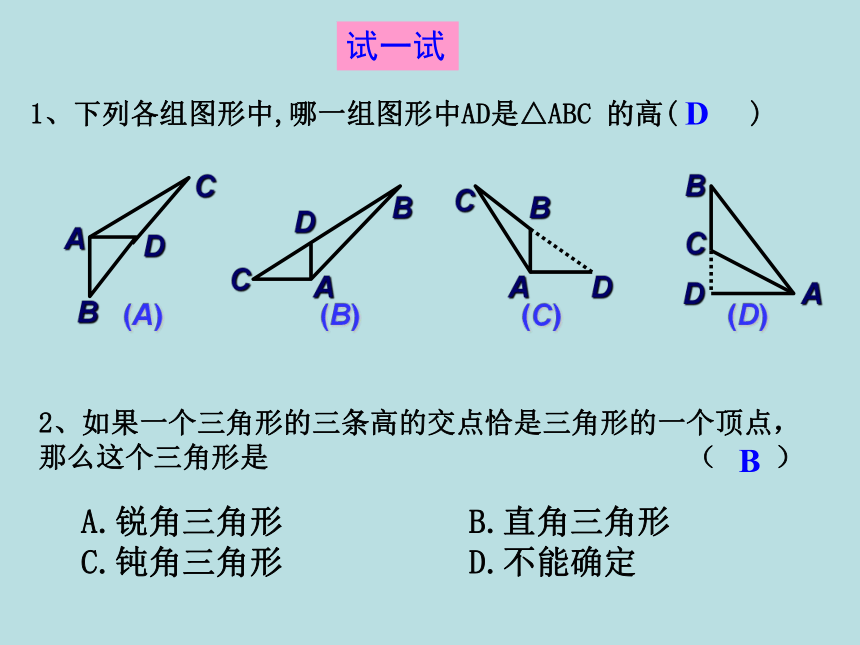
②在钝角的对边上在三角形内部在直角顶点在三角形外部小结:三角形的高2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 ( )A.锐角三角形 B.直角三角形
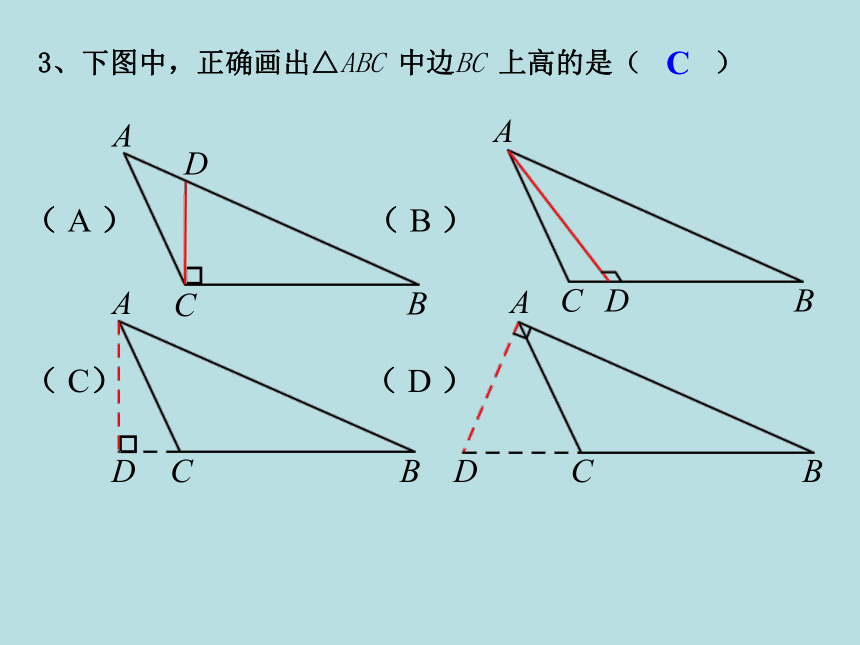
C.钝角三角形 D.不能确定BD试一试1、下列各组图形中,哪一组图形中AD是△ABC 的高( )C3、下图中,正确画出△ABC 中边BC 上高的是( )S乙>S甲=S丙4、下列各阴影部分的面积有何关系?在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?●●EFO三角形的中线三角形的三条中线相交于一点,交点在三角形的内部.也就是说:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积例1:如图,在△ABC中,AD,AE分别是BC边上的中线和高.试判断△ABD和△ADC的面积有何关系?②三角形的中线是一条线段。①任何三角形有三条中线,并且都在三角形的内部,交与一点。③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。三角形三条中线的交点叫做三角形的重心.三角形中线的特点如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .22BD6 cm2试一试三角形的角平分线准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.∠1和∠2 有什么关系?叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部三角形的角平分线∵BE是△ABC的角平分线∴_______=_______= ____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF三角形的角平分线是一条线段 , 角的平分线是一条射线。三角形的角平分线与角的平分线有什么区别?角平分线的理解例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数解:∵BD、CE分别是△ABC的角平分线例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(2)当∠A=40°时,求∠BOC的度数解:∵BD、CE分别是△ABC的角平分线例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(3)当∠A= x°时,求∠BOC的度数(用含x代数式表示)解:∵BD、CE分别是△ABC的角平分线高、中线与角平分线的比较1.如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的.①AD是⊿ABE的角平分线 ( )②BE是⊿ABD边AD上的中线 ( )③BE是⊿ABC边AC上的中线 ( )④CH是⊿ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√试一试2、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。( )3、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为 。4、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。×202D1.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质 ( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一做一做2.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是 ( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DEC3.试把一块三角形煎饼分成大小相同的4块,有多少种分法?1.在△ABC中,AE,AD分别是BC边上的中线和高.说明△ABE的面积与△AEC的面积相等.解:∵ AE是BC边上的中线∴ BE = EC∴∵做一做 ACBEFD2.如图点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S, 求△DEF的面积. 你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗? △AEF和△FBD的面积呢?三角形的角平分线、中线、高线的比较相同点:(1)都是线段(2)都从顶点画出(3)所在直线都相交于一点不同点:角平分线反映的是角的相等关系中线反映的是线段的相等关系高线反映的是它和对边或对边所在直线的垂直关系小结好好学习天天向上
2.了解三角形的高、中线、和角平分线的性质,并能应用它解决一些问题.
3.感受数学知识的广泛用途和科学探究精神.2.线段中点的定义:3.角平分线的定义:1.垂线的定义:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.把一条线段分成两条相等的线段的点.当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.忆一忆你还记得 “过一点画已知直线的垂线” 吗?过三角形的一个顶点,你能画出它到对边的垂线段吗?忆一忆A从三角形的一个顶点BC向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.如图, 线段AD是BC边上的高.任意画一个锐角△ABC,请你画出BC边上的高.三角形的高从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高.AD⊥BC,则AD是△ABC的BC边上的高AD是△ABC的BC边上的高,则AD⊥BC,∠ADB=900(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?锐角三角形的三条高交于同一点.(3)锐角三角形的三条高是在三角形的内部还是外部?锐角三角形的三条高都在三角形的内部.ABCDEF锐角三角形的三条高ABC(1) 画出直角三角形的三条高,直角边BC边上的高是 ;AB直角边AB边上的高是 ;CB它们有怎样的位置关系?直角三角形的三条高交于直角顶点.D斜边AC边上的高是 ;BD●直角三角形的三条高(1) 钝角三角形的三条高交于一点吗?钝角三角形的三条高不相交于一点它们所在的直线交于一点吗?钝角三角形的三条高所在直线交于一点O钝角三角形的三条高333都在三角
形内部直角边上的高分别与另一条直角边重合,还有一条高在三角形内部夹钝角两边上的高在三角形外部,另一条高在内部在相应顶点的对边上①是直角的顶点
②在斜边上①在相应顶点的对边的延长线上
②在钝角的对边上在三角形内部在直角顶点在三角形外部小结:三角形的高2、如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 ( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定BD试一试1、下列各组图形中,哪一组图形中AD是△ABC 的高( )C3、下图中,正确画出△ABC 中边BC 上高的是( )S乙>S甲=S丙4、下列各阴影部分的面积有何关系?在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边的中线.D∵AD是△ ABC的中线任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?●●EFO三角形的中线三角形的三条中线相交于一点,交点在三角形的内部.也就是说:三角形的任意一条中线把这个三角形分成了两个面积相等的三角形.如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积例1:如图,在△ABC中,AD,AE分别是BC边上的中线和高.试判断△ABD和△ADC的面积有何关系?②三角形的中线是一条线段。①任何三角形有三条中线,并且都在三角形的内部,交与一点。③三角形的任意一条中线把这个三角形分成了两个面积相等的三角形。三角形三条中线的交点叫做三角形的重心.三角形中线的特点如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE = EC;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .22BD6 cm2试一试三角形的角平分线准备一个三角形纸片ABC ,按图所示的方法折叠,展开后,折痕BD 把∠ABC 分成∠1和∠2 两个角.∠1和∠2 有什么关系?叫做三角形的角平分线。ABCD∵AD是 △ ABC的角平分线任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的内部三角形的角平分线∵BE是△ABC的角平分线∴_______=_______= ____∴∠ACB=2______=2______∠ABE∠CBE∠ABC∠ACF∵CF是△ABC的角平分线∠BCF三角形的角平分线是一条线段 , 角的平分线是一条射线。三角形的角平分线与角的平分线有什么区别?角平分线的理解例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(1)当∠ABC=60°,∠ACB=80°时,求∠BOC的度数解:∵BD、CE分别是△ABC的角平分线例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(2)当∠A=40°时,求∠BOC的度数解:∵BD、CE分别是△ABC的角平分线例2:如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.(3)当∠A= x°时,求∠BOC的度数(用含x代数式表示)解:∵BD、CE分别是△ABC的角平分线高、中线与角平分线的比较1.如图,在⊿ABC中, ∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,CF⊥AD于H,判断下列说法那些是正确的,哪些是错误的.①AD是⊿ABE的角平分线 ( )②BE是⊿ABD边AD上的中线 ( )③BE是⊿ABC边AC上的中线 ( )④CH是⊿ACD边AD上的高 ( )三角形的高、中线与角平分线都是线段×××√试一试2、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。( )3、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为 。4、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。×202D1.如图1所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180°,使点B 落在点B′的位置,则线段AC具有性质 ( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一做一做2.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是 ( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BD=EC
D.∠C的对边是DEC3.试把一块三角形煎饼分成大小相同的4块,有多少种分法?1.在△ABC中,AE,AD分别是BC边上的中线和高.说明△ABE的面积与△AEC的面积相等.解:∵ AE是BC边上的中线∴ BE = EC∴∵做一做 ACBEFD2.如图点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S, 求△DEF的面积. 你可以这样考虑:
(1)连结AD. △ADC的面积是多少?
(2)由第(1)题,你能求出△DEC的面积吗? △AEF和△FBD的面积呢?三角形的角平分线、中线、高线的比较相同点:(1)都是线段(2)都从顶点画出(3)所在直线都相交于一点不同点:角平分线反映的是角的相等关系中线反映的是线段的相等关系高线反映的是它和对边或对边所在直线的垂直关系小结好好学习天天向上
