11.2.1三角形的内角(2课时)
文档属性
| 名称 | 11.2.1三角形的内角(2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 470.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-30 09:07:26 | ||
图片预览



文档简介
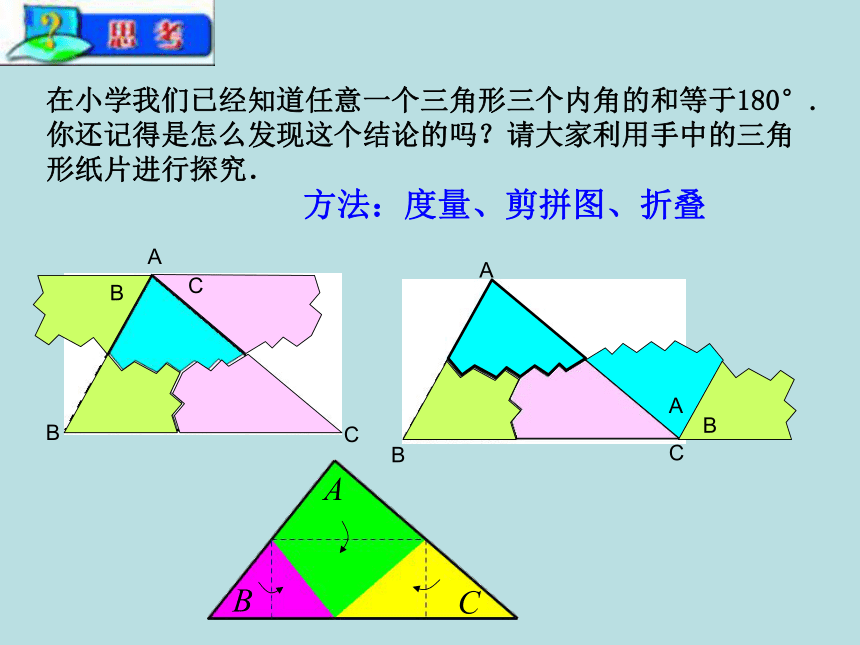
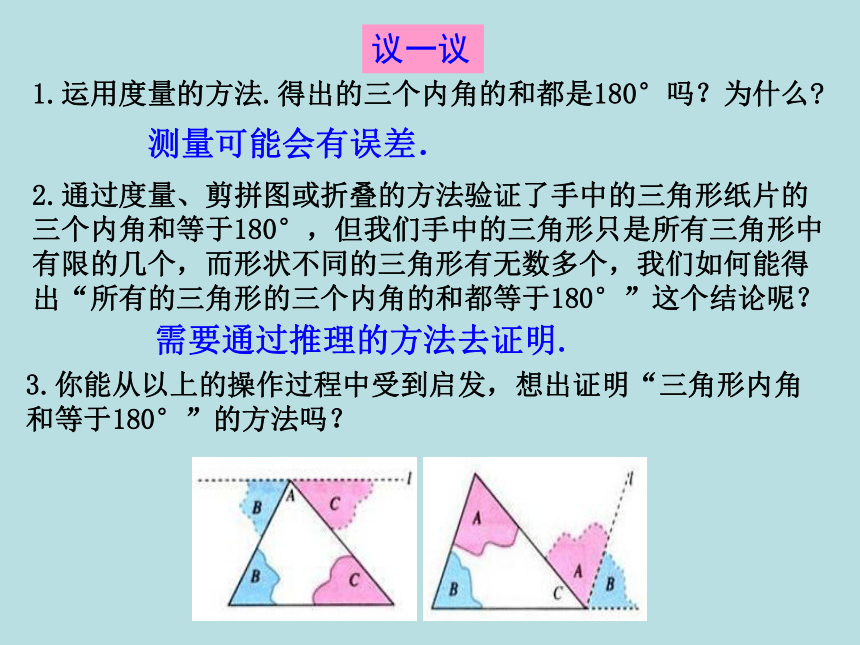
课件38张PPT。§11.2.1 三角形的内角(第1课时)ABCABC在小学我们已经知道任意一个三角形三个内角的和等于180°.你还记得是怎么发现这个结论的吗?请大家利用手中的三角形纸片进行探究.方法:度量、剪拼图、折叠 测量可能会有误差. 1.运用度量的方法.得出的三个内角的和都是180°吗?为什么?2.通过度量、剪拼图或折叠的方法验证了手中的三角形纸片的三个内角和等于180°,但我们手中的三角形只是所有三角形中有限的几个,而形状不同的三角形有无数多个,我们如何能得出“所有的三角形的三个内角的和都等于180°”这个结论呢?议一议需要通过推理的方法去证明.3.你能从以上的操作过程中受到启发,想出证明“三角形内角和等于180°”的方法吗?在图中,∠B 和∠C 分别拼在∠A 的左右,三个角合起来形成一个平角,出现了一条过点A 的直线l,直线l 与边BC 有什么位置关系?在操作过程中,我们发现了与边BC平行的直线l,由此,你又能受到什么启发?你能发现证明 “三角形内角和等于180°”的思路吗?证明:过点A 作直线l ,使l ∥BC.
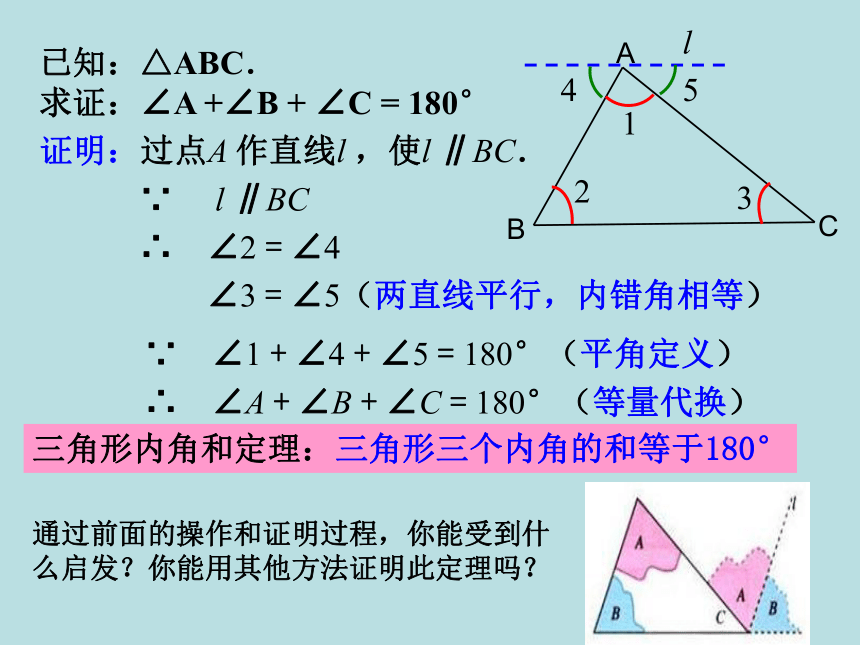
∵ l ∥BC
∴ ∠2 = ∠4
∠3 = ∠5(两直线平行,内错角相等)已知:△ABC.
求证:∠A +∠B + ∠C = 180°∵ ∠1 + ∠4 + ∠5 = 180°(平角定义)
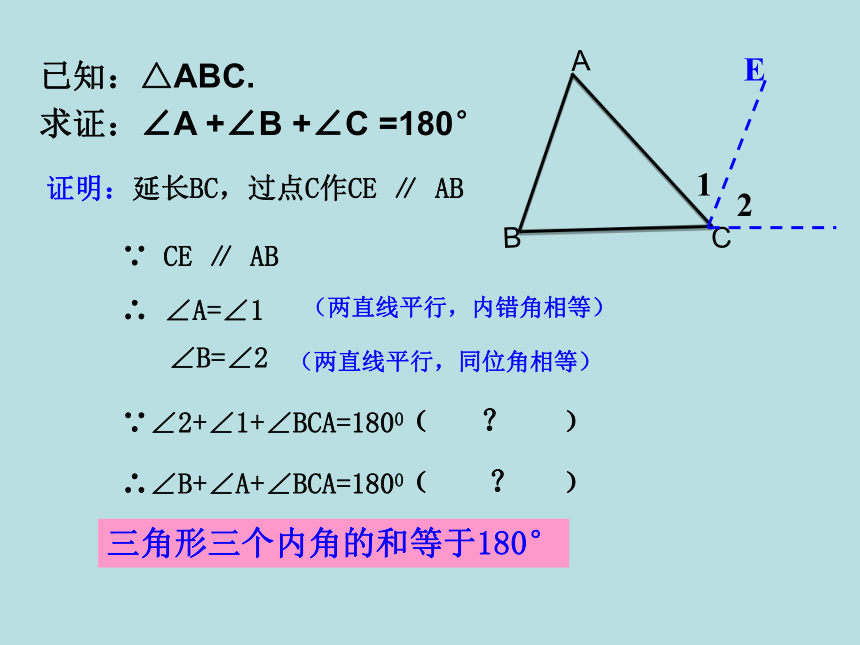
∴ ∠A + ∠B + ∠C = 180°(等量代换)三角形内角和定理:三角形三个内角的和等于180°2314l5通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?证明:延长BC,过点C作CE ∥ ABE∵ CE ∥ AB(两直线平行,内错角相等)∴ ∠A=∠1∠B=∠2(两直线平行,同位角相等)∵∠2+∠1+∠BCA=1800﹙ ? ﹚
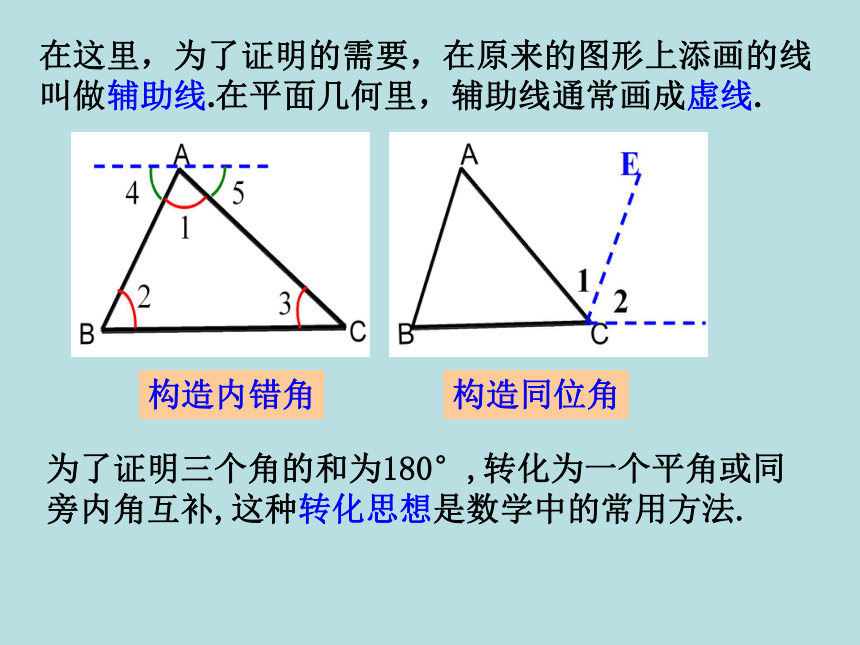
∴∠B+∠A+∠BCA=1800﹙ ? ﹚12三角形三个内角的和等于180°在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.构造内错角构造同位角1.在△ABC中,∠A=35°,∠ B=43°,则∠ C= ___.
2.在△ABC中,∠C=90°,∠B=50°, 则∠A = ___.
3.在△ABC中, ∠A=40°,∠A=2∠B,则∠C = ___.
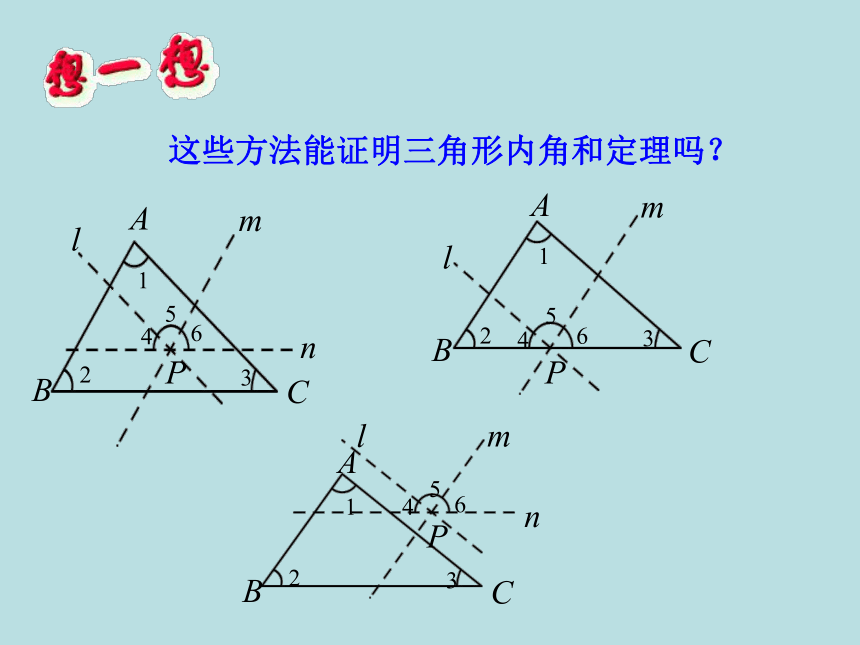
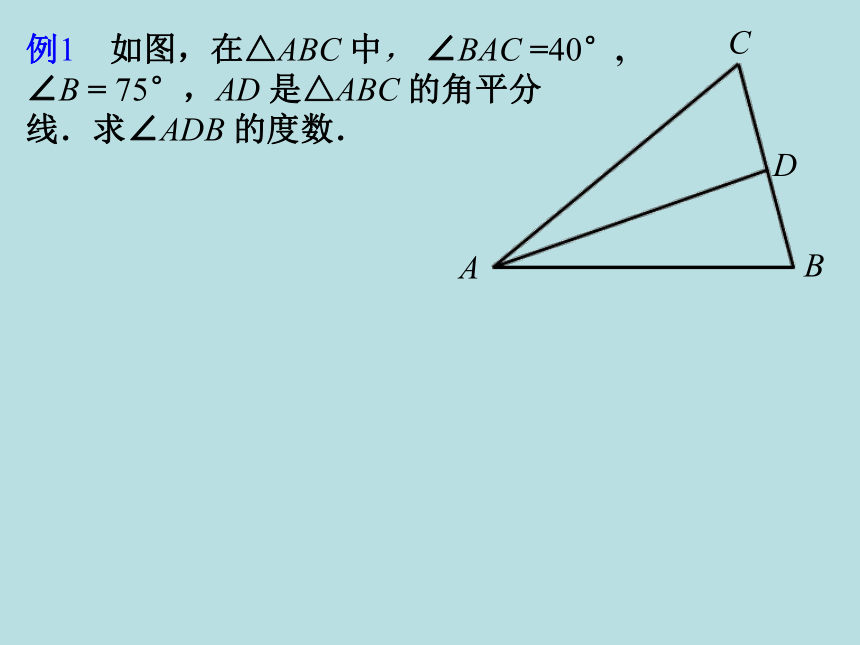
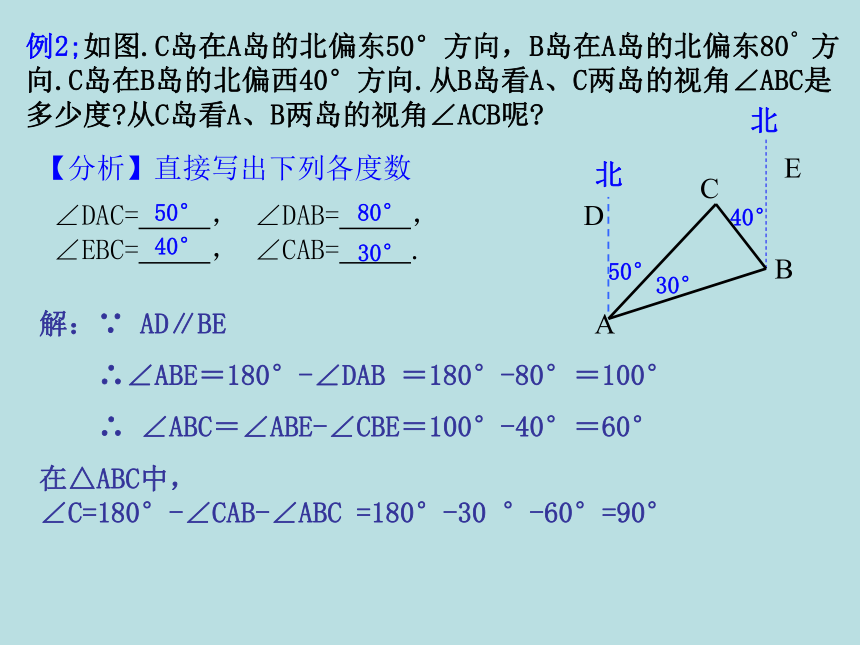
4.在△ABC中,∠A=75°,∠ B-∠ C=15°,则∠ C= __. 102°试一试40°120°45°5.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数.解:设三个内角度数分别为:x、3x、5x.由三角形内角和为180°得x+3x+5x = 180°解得 x = 20°所以三个内角度数分别为20°,60°,100°这些方法能证明三角形内角和定理吗? 例1 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数.例2;如图.C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向.C岛在B岛的北偏西40°方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?【分析】直接写出下列各度数∠DAC= , ∠DAB= , ∠EBC= , ∠CAB= .解:∵ AD∥BE
∴∠ABE=180°-∠DAB =180°-80°=100°
∴ ∠ABC=∠ABE-∠CBE=100°-40°=60°
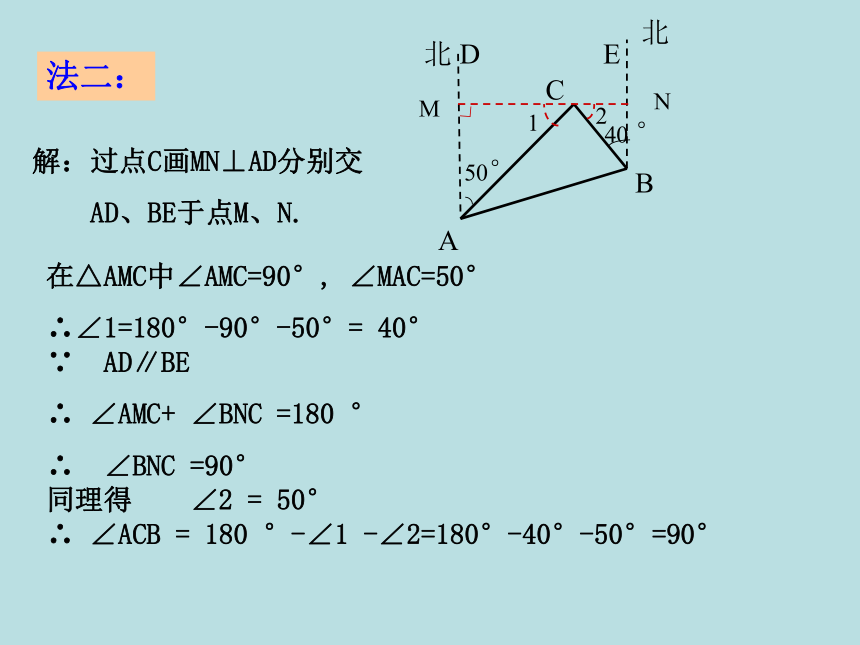
在△ABC中, ∠C=180°-∠CAB-∠ABC =180°-30 °-60°=90°50°30°40°50°80°40°30°DCE北A50°∟B40 °北MN 在△AMC中∠AMC=90°, ∠MAC=50°
∴∠1=180°-90°-50°= 40° ∵ AD∥BE
∴ ∠AMC+ ∠BNC =180 °
∴ ∠BNC =90° 同理得 ∠2 = 50° ∴ ∠ACB = 180 °-∠1 -∠2=180°-40°-50°=90° 解:过点C画MN⊥AD分别交
AD、BE于点M、N.12法二:B1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50°F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE=40°∴ ∠ACB=∠1﹢∠2=50°+40°=90°法三:解:在△ACD中 ∠CAD =30° ∠D=90°
∴ ∠ACD =180° -30° -90°=60°
在△BCD中 ∠CBD= 45° ∠D=90°
∴ ∠BCD =180°- 90°-45°=45°
∴ ∠ACB =∠ACD- ∠BCD = 60°-45°1.如图,从A处观测C处时仰角∠CAD=30°.从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?练一练2.如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°.∠B=∠D=40°.求∠C的度数.D解:在△ABC中 ∠B+∠1+∠BAC=180°
在△ACD中 ∠D+∠2+∠DAC=180°
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360°
即 ∠B+∠D+ ∠BCD +∠BAD= 360°
40°+40°+ ∠BCD +150° = 360°
∴ ∠BCD = 360°-40°- 40°- 150°=130°另解: 由题意得 ∠BAC=∠DAC=75°
在△ABC中
∠BCA =180°-∠BAC-∠B=180°-75°-40°=65°
∴ ∠ACD = ∠ BCD = 65 °
∴ ∠BCD = ∠ACD + ∠ BCD =130 °1、三角形内角和的定理:三角形三个内角的和等于180°.
2、通过思考、去探究、去总结三角形内角和的定理,并且证明方法不止一种.
3、探索到一个数学规律,最终还须证明.
4、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角.小结???????????????????????????????????????????????????? 1.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为__.做一做75° 5 2 3 4 2.如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3= __.110° 做一做1.一个三角形中最多有__个直角?为什么?
2.一个三角形中最多有__个钝角?为什么?
3.一个三角形中至少有__个锐角?为什么?
4.任意一个三角形中,最大的角不能小于__.11260°5、如图,一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )A.带①去 B.带②去
C.带③去 D.带①和②去C6.已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.解:设∠A= x ,则∠C =∠ABC =2x. ∴x + 2x + 2x =180 (三角形内角和定理).解方程,得x =360
∴ ∠C = 2×360 = 720ABCD在△BDC中,
∵∠BDC=90°(已知)
∴∠DBC=180°-90°-72°(三角形内角和定理)
∴∠DBC=18°┓好好学习天天向上§11.2.1三角形的内角(第2课时)复习:求出图中x的值探索直角三角形的性质 问题2 在△ABC 中,若∠C =90°,你能求出∠A,
∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?
利用上面的结果,你能得出什么结论?直角三角形的两个锐角互余. 探索直角三角形的性质 直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .探索直角三角形的性质在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 问题3 此性质的几何推理格式该怎样表示?例题讲解 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么? 分析:两个角的关系是
什么?这两个角分别在什么
三角形中?你如何验证自己
的想法?例题讲解解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°, 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?例题讲解解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等). 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?探索直角三角形的判定 问题4 我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得出什么
结论?这个结论成立吗?如何验证你的想法? 利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形. 探索直角三角形的判定 问题5 类比性质的几何推理格式,判定的几何推
理格式又该怎样表示? 推理格式:
在Rt△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.相等.
同角的余角相等. 课堂练习 练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?课堂练习 变式1 若∠ACD =∠B,∠ACB =90°,则CD 是
△ACB 的高吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式2 若∠ACD =∠B,CD ⊥AB,△ACB 为直角
三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式3 如图,若∠C =90°,∠AED =∠B,△ADE
是直角三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.
(证明过程略).【课堂练习】1、课本14页1题,
变式你还能说一下∠A与∠BCD的关系吗?
选作请你找出图中所有的互余的角并写下来解:∠B=∠ACD。理由:
在Rt △ABC中, ∠ACB =90°
∴ ∠B= 90°— ∠A
∵CD⊥AB
∴ △ACD是直角三角形
∴∠ACD= 90°— ∠A
∴ ∠B=∠ACD
思考:如果是直角三角形则两锐角互余,反之,如果在一个三角形中两角互余,则这个三角形是直角三角形吗? Z.xxk已知:在三角形ABC中,∠ A+ ∠B=90°。
求证: ∠C =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,
而∠A+ ∠B =90°
∴ ∠C =90°好好学习天天向上
∵ l ∥BC
∴ ∠2 = ∠4
∠3 = ∠5(两直线平行,内错角相等)已知:△ABC.
求证:∠A +∠B + ∠C = 180°∵ ∠1 + ∠4 + ∠5 = 180°(平角定义)
∴ ∠A + ∠B + ∠C = 180°(等量代换)三角形内角和定理:三角形三个内角的和等于180°2314l5通过前面的操作和证明过程,你能受到什么启发?你能用其他方法证明此定理吗?证明:延长BC,过点C作CE ∥ ABE∵ CE ∥ AB(两直线平行,内错角相等)∴ ∠A=∠1∠B=∠2(两直线平行,同位角相等)∵∠2+∠1+∠BCA=1800﹙ ? ﹚
∴∠B+∠A+∠BCA=1800﹙ ? ﹚12三角形三个内角的和等于180°在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线.在平面几何里,辅助线通常画成虚线.为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.构造内错角构造同位角1.在△ABC中,∠A=35°,∠ B=43°,则∠ C= ___.
2.在△ABC中,∠C=90°,∠B=50°, 则∠A = ___.
3.在△ABC中, ∠A=40°,∠A=2∠B,则∠C = ___.
4.在△ABC中,∠A=75°,∠ B-∠ C=15°,则∠ C= __. 102°试一试40°120°45°5.已知:三角形三个内角的度数之比为1:3:5,求这三个内角的度数.解:设三个内角度数分别为:x、3x、5x.由三角形内角和为180°得x+3x+5x = 180°解得 x = 20°所以三个内角度数分别为20°,60°,100°这些方法能证明三角形内角和定理吗? 例1 如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数.例2;如图.C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向.C岛在B岛的北偏西40°方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?【分析】直接写出下列各度数∠DAC= , ∠DAB= , ∠EBC= , ∠CAB= .解:∵ AD∥BE
∴∠ABE=180°-∠DAB =180°-80°=100°
∴ ∠ABC=∠ABE-∠CBE=100°-40°=60°
在△ABC中, ∠C=180°-∠CAB-∠ABC =180°-30 °-60°=90°50°30°40°50°80°40°30°DCE北A50°∟B40 °北MN 在△AMC中∠AMC=90°, ∠MAC=50°
∴∠1=180°-90°-50°= 40° ∵ AD∥BE
∴ ∠AMC+ ∠BNC =180 °
∴ ∠BNC =90° 同理得 ∠2 = 50° ∴ ∠ACB = 180 °-∠1 -∠2=180°-40°-50°=90° 解:过点C画MN⊥AD分别交
AD、BE于点M、N.12法二:B1250°40°解: 过点C画CF∥AD ∴ ∠1=∠DAC=50°F∵ CF∥AD, 又AD ∥BE∴ CF∥ BE∴∠2=∠CBE=40°∴ ∠ACB=∠1﹢∠2=50°+40°=90°法三:解:在△ACD中 ∠CAD =30° ∠D=90°
∴ ∠ACD =180° -30° -90°=60°
在△BCD中 ∠CBD= 45° ∠D=90°
∴ ∠BCD =180°- 90°-45°=45°
∴ ∠ACB =∠ACD- ∠BCD = 60°-45°1.如图,从A处观测C处时仰角∠CAD=30°.从B处观测C处时仰角∠CBD=45°.从C处观测A、B两处时视角∠ACB是多少?练一练2.如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°.∠B=∠D=40°.求∠C的度数.D解:在△ABC中 ∠B+∠1+∠BAC=180°
在△ACD中 ∠D+∠2+∠DAC=180°
∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360°
即 ∠B+∠D+ ∠BCD +∠BAD= 360°
40°+40°+ ∠BCD +150° = 360°
∴ ∠BCD = 360°-40°- 40°- 150°=130°另解: 由题意得 ∠BAC=∠DAC=75°
在△ABC中
∠BCA =180°-∠BAC-∠B=180°-75°-40°=65°
∴ ∠ACD = ∠ BCD = 65 °
∴ ∠BCD = ∠ACD + ∠ BCD =130 °1、三角形内角和的定理:三角形三个内角的和等于180°.
2、通过思考、去探究、去总结三角形内角和的定理,并且证明方法不止一种.
3、探索到一个数学规律,最终还须证明.
4、三角形内角和的定理证明中,添加辅助线的实质是通过平行线来移动角.小结???????????????????????????????????????????????????? 1.将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为__.做一做75° 5 2 3 4 2.如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3= __.110° 做一做1.一个三角形中最多有__个直角?为什么?
2.一个三角形中最多有__个钝角?为什么?
3.一个三角形中至少有__个锐角?为什么?
4.任意一个三角形中,最大的角不能小于__.11260°5、如图,一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )A.带①去 B.带②去
C.带③去 D.带①和②去C6.已知:在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.解:设∠A= x ,则∠C =∠ABC =2x. ∴x + 2x + 2x =180 (三角形内角和定理).解方程,得x =360
∴ ∠C = 2×360 = 720ABCD在△BDC中,
∵∠BDC=90°(已知)
∴∠DBC=180°-90°-72°(三角形内角和定理)
∴∠DBC=18°┓好好学习天天向上§11.2.1三角形的内角(第2课时)复习:求出图中x的值探索直角三角形的性质 问题2 在△ABC 中,若∠C =90°,你能求出∠A,
∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?
利用上面的结果,你能得出什么结论?直角三角形的两个锐角互余. 探索直角三角形的性质 直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .探索直角三角形的性质在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 问题3 此性质的几何推理格式该怎样表示?例题讲解 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么? 分析:两个角的关系是
什么?这两个角分别在什么
三角形中?你如何验证自己
的想法?例题讲解解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°, 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?例题讲解解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等). 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?探索直角三角形的判定 问题4 我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得出什么
结论?这个结论成立吗?如何验证你的想法? 利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形. 探索直角三角形的判定 问题5 类比性质的几何推理格式,判定的几何推
理格式又该怎样表示? 推理格式:
在Rt△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.相等.
同角的余角相等. 课堂练习 练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?课堂练习 变式1 若∠ACD =∠B,∠ACB =90°,则CD 是
△ACB 的高吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式2 若∠ACD =∠B,CD ⊥AB,△ACB 为直角
三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式3 如图,若∠C =90°,∠AED =∠B,△ADE
是直角三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.
(证明过程略).【课堂练习】1、课本14页1题,
变式你还能说一下∠A与∠BCD的关系吗?
选作请你找出图中所有的互余的角并写下来解:∠B=∠ACD。理由:
在Rt △ABC中, ∠ACB =90°
∴ ∠B= 90°— ∠A
∵CD⊥AB
∴ △ACD是直角三角形
∴∠ACD= 90°— ∠A
∴ ∠B=∠ACD
思考:如果是直角三角形则两锐角互余,反之,如果在一个三角形中两角互余,则这个三角形是直角三角形吗? Z.xxk已知:在三角形ABC中,∠ A+ ∠B=90°。
求证: ∠C =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,
而∠A+ ∠B =90°
∴ ∠C =90°好好学习天天向上
