11.2.2三角形的外角
文档属性
| 名称 | 11.2.2三角形的外角 |  | |
| 格式 | zip | ||
| 文件大小 | 522.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-30 09:08:38 | ||
图片预览

文档简介
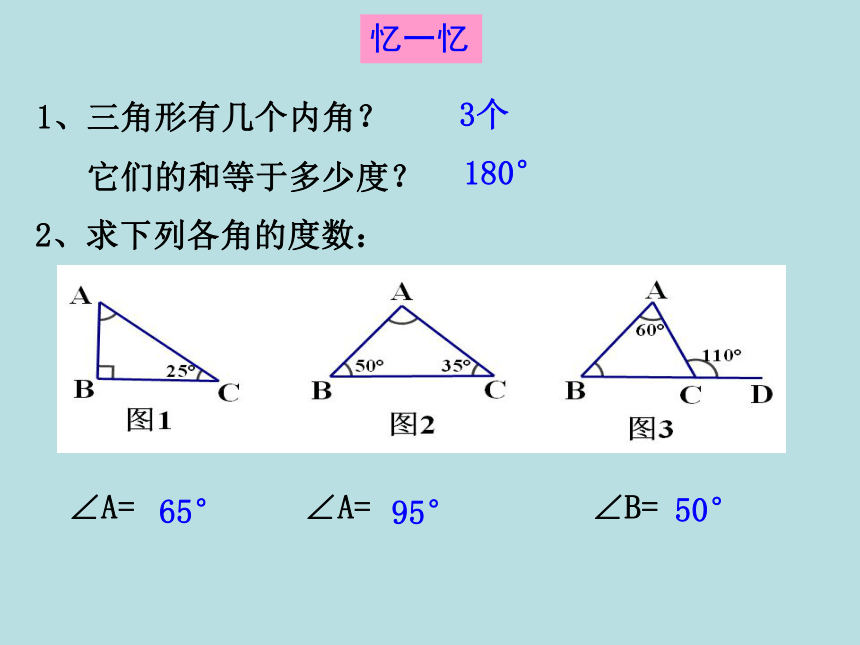
课件15张PPT。§11.2.2 三角形的外角2、求下列各角的度数:1、三角形有几个内角?
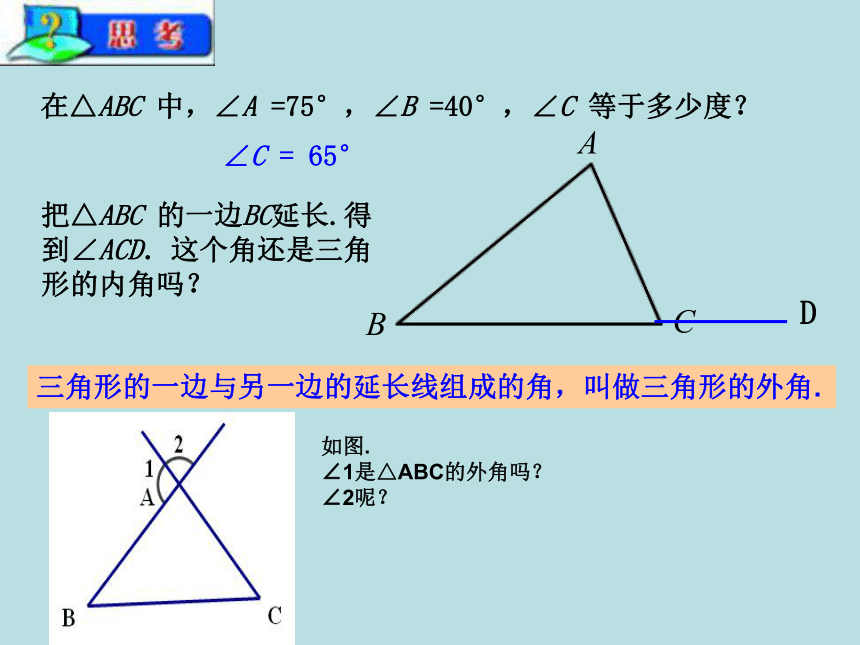
它们的和等于多少度?65°3个180°95°∠A= ∠A= ∠B=50°忆一忆在△ABC 中,∠A =75°,∠B =40°,∠C 等于多少度?∠C = 65°把△ABC 的一边BC延长.得到∠ACD.这个角还是三角形的内角吗? 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.D如图.
∠1是△ABC的外角吗?
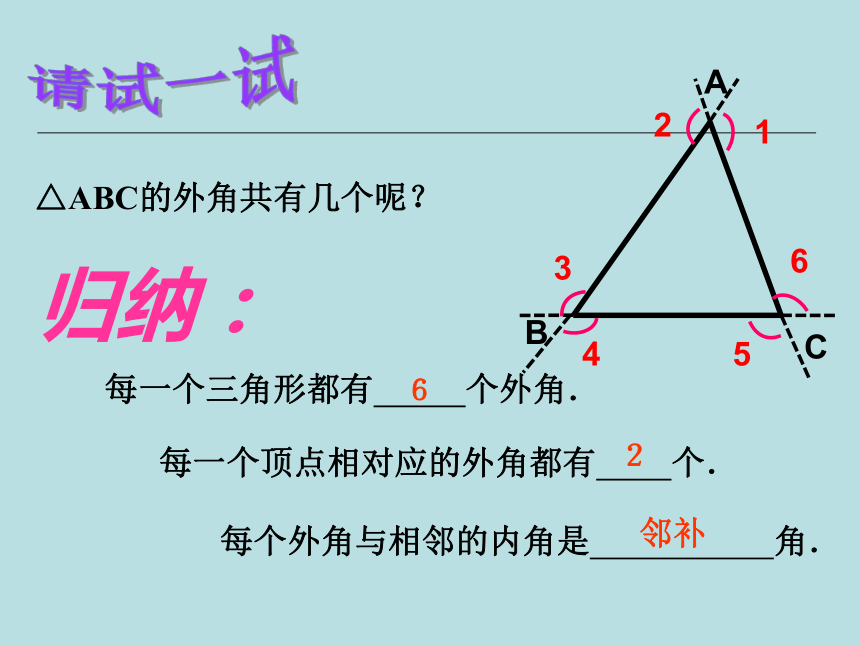
∠2呢?△ABC的外角共有几个呢?请试一试归纳: 每一个三角形都有 个外角.
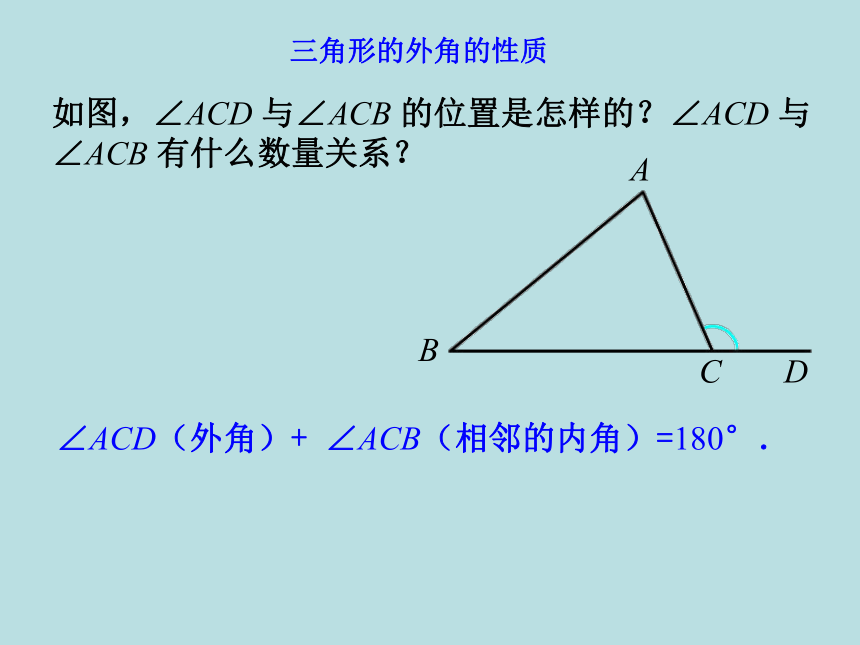
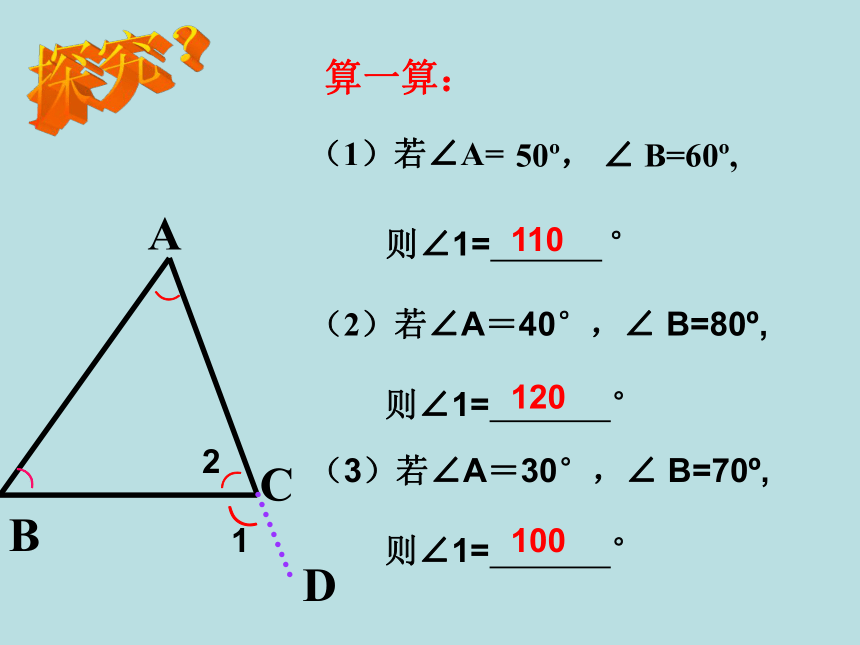
每一个顶点相对应的外角都有 个. 每个外角与相邻的内角是 角.ABC12346562邻补 ∠ACD(外角)+ ∠ACB(相邻的内角)=180°.如图,∠ACD 与∠ACB 的位置是怎样的?∠ACD 与∠ACB 有什么数量关系?三角形的外角的性质ABCD算一算:⌒⌒⌒⌒11012012100想一想:
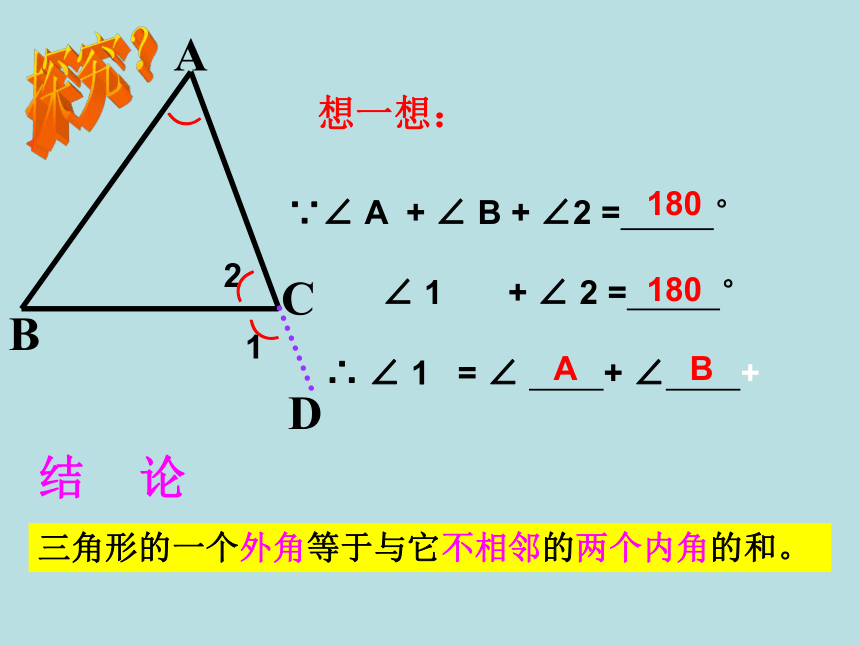
∵∠ A + ∠ B + ∠2 = °
∠ 1 + ∠ 2 = °
∴ ∠ 1 = ∠ + ∠ +结 论三角形的一个外角等于与它不相邻的两个内角的和。CBAD180180AB21⌒⌒⌒如图,
∵ ∠ACD +∠ACB =180°,
∠A +∠B +∠ACB =180°,
∴ ∠ACD =∠A +∠B.如图,∠ACD 与∠A,∠B 的位置是怎样的?∠ACD 与∠A,∠B 的大小有什么关系?你能证明你的结论吗?三角形的外角的性质三角形内角和定理的推论:
三角形的一个外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论,和定理一样,推论可以作为进一步推理的依据.如图,口答:
(1)∠1 = + ;
(2)∠2 = + .∠C∠3∠DAC∠4如图,说出图形中∠1 的度数.图中∠1的度数依次为:90°,85°, 95°,45°.如图,说出图形中∠1 和∠2 的度数:例 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?解法一:
∵ ∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴ ∠BAE +∠CBF +∠ACD=
(∠2 +∠3)+(∠1 +∠3)+ (∠1 +∠2)= 2(∠1 +∠2 +∠3).
∵ ∠1 +∠2 +∠3 =180°,
∴ ∠BAE +∠CBF +∠ACD
= 2×180°=360°.解法二:
由∠1 +∠BAE =180°
∠2 +∠CBF =180°
∠3 +∠ACD =180°
得∠1 +∠2 +∠3 + ∠BAE
+∠CBF +∠ACD = 540°例 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?由∠1 + ∠2 + ∠3 =180°
得∠BAE + ∠CBF + ∠ACD
= 540°- 180°
=360°如图,D是△ABC 的BC 边上一点,∠B =∠BAD,∠ADC=80°,∠BAC =70°
求:(1)∠B 的度数;(2)∠C 的度数.好好学习天天向上
它们的和等于多少度?65°3个180°95°∠A= ∠A= ∠B=50°忆一忆在△ABC 中,∠A =75°,∠B =40°,∠C 等于多少度?∠C = 65°把△ABC 的一边BC延长.得到∠ACD.这个角还是三角形的内角吗? 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.D如图.
∠1是△ABC的外角吗?
∠2呢?△ABC的外角共有几个呢?请试一试归纳: 每一个三角形都有 个外角.
每一个顶点相对应的外角都有 个. 每个外角与相邻的内角是 角.ABC12346562邻补 ∠ACD(外角)+ ∠ACB(相邻的内角)=180°.如图,∠ACD 与∠ACB 的位置是怎样的?∠ACD 与∠ACB 有什么数量关系?三角形的外角的性质ABCD算一算:⌒⌒⌒⌒11012012100想一想:
∵∠ A + ∠ B + ∠2 = °
∠ 1 + ∠ 2 = °
∴ ∠ 1 = ∠ + ∠ +结 论三角形的一个外角等于与它不相邻的两个内角的和。CBAD180180AB21⌒⌒⌒如图,
∵ ∠ACD +∠ACB =180°,
∠A +∠B +∠ACB =180°,
∴ ∠ACD =∠A +∠B.如图,∠ACD 与∠A,∠B 的位置是怎样的?∠ACD 与∠A,∠B 的大小有什么关系?你能证明你的结论吗?三角形的外角的性质三角形内角和定理的推论:
三角形的一个外角等于与它不相邻的两个内角的和.
推论是由定理直接推出的结论,和定理一样,推论可以作为进一步推理的依据.如图,口答:
(1)∠1 = + ;
(2)∠2 = + .∠C∠3∠DAC∠4如图,说出图形中∠1 的度数.图中∠1的度数依次为:90°,85°, 95°,45°.如图,说出图形中∠1 和∠2 的度数:例 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?解法一:
∵ ∠BAE =∠2 +∠3,
∠CBF =∠1 +∠3,
∠ACD =∠1 +∠2,
∴ ∠BAE +∠CBF +∠ACD=
(∠2 +∠3)+(∠1 +∠3)+ (∠1 +∠2)= 2(∠1 +∠2 +∠3).
∵ ∠1 +∠2 +∠3 =180°,
∴ ∠BAE +∠CBF +∠ACD
= 2×180°=360°.解法二:
由∠1 +∠BAE =180°
∠2 +∠CBF =180°
∠3 +∠ACD =180°
得∠1 +∠2 +∠3 + ∠BAE
+∠CBF +∠ACD = 540°例 如图,∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,它们的和是多少?由∠1 + ∠2 + ∠3 =180°
得∠BAE + ∠CBF + ∠ACD
= 540°- 180°
=360°如图,D是△ABC 的BC 边上一点,∠B =∠BAD,∠ADC=80°,∠BAC =70°
求:(1)∠B 的度数;(2)∠C 的度数.好好学习天天向上
