2023年广东省广州市中考数学模拟试卷(二)(含答案)
文档属性
| 名称 | 2023年广东省广州市中考数学模拟试卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 18:49:52 | ||
图片预览


文档简介
2023年广州市中考数学模拟试卷(二)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)一个长方体礼盒的展开图如图所示(重叠部分不计)则该长方体的表面积为( )
A.34 B.36 C.42 D.46
2.(3分)云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列的云纹图案中,是中心对称图形的是( )
A. B.
C. D.
3.(3分)若代数式有意义,则x的取值范围是( )
A.x≥2 B.x≥0 C.x≥0且x≠2 D.x≠2
4.(3分)若一个正比例函数的图象经过点A(1,﹣2),B(m,4)两点,则m的值为( )
A.2 B.﹣2 C.8 D.﹣8
5.(3分)下列计算正确的是( )
A. B.
C. D.
6.(3分)实数a,b,c在数轴上的对应点的位置如图所示,如果a+b=0,那么下列结论正确的是( )
A.> B.a+c<0 C.abc<0 D.
7.(3分)在一次联欢晚会上,某班进行以下游戏,准备两个不透明的袋子和7个小球(大小、形状完全一样),一个袋子里放置3个小球,球面上分别写着“好”“运”“来”,另一个袋子里放置4个小球,球面上分别写着“新”“年”“好”“运”.现从两个袋子里各随机抽取一个球,球面上的字可以组成“好运”字样的获得一等奖,则获得一等奖的概率为( )
A. B. C. D.
8.(3分)如图,一次函数y1=x与二次函数图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )
A. B.
C. D.
9.(3分)已知四边形ABCD是平行四边形,则下列结论中正确的是( )
A.当AB⊥BD时,它是菱形
B.当AC=BD时,它是正方形
C.当∠ABC=90°时,它是矩形
D.当AB=BC时,它是矩形
10.(3分)如图,矩形ABCD中AB是3cm,BC是2cm,一个边长为1cm的小正方形沿着矩形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形箭头的方向是( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
工种 电工 木工 瓦工
人数 5 4 5
每人每月工资(元) 7000 6000 5000
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差 (填“变小”“不变”或“变大”).
12.(3分)因式分解:m2﹣4m= .
13.(3分)如图,在 ABCD中,以点D为圆心,以DA的长为半径画弧交边BC于点E,连接AE,若∠ADE=30°,则∠AEB= .
14.(3分)方程的解为 .
15.(3分)如图,四边形ABCD是正方形,曲线DEFGH…叫做“正方形的渐开线“,其中,,,,…依次连接,它们的圆心依次按A、B、C、D循环.当AB=1时,曲线DEFGH的长度是 .
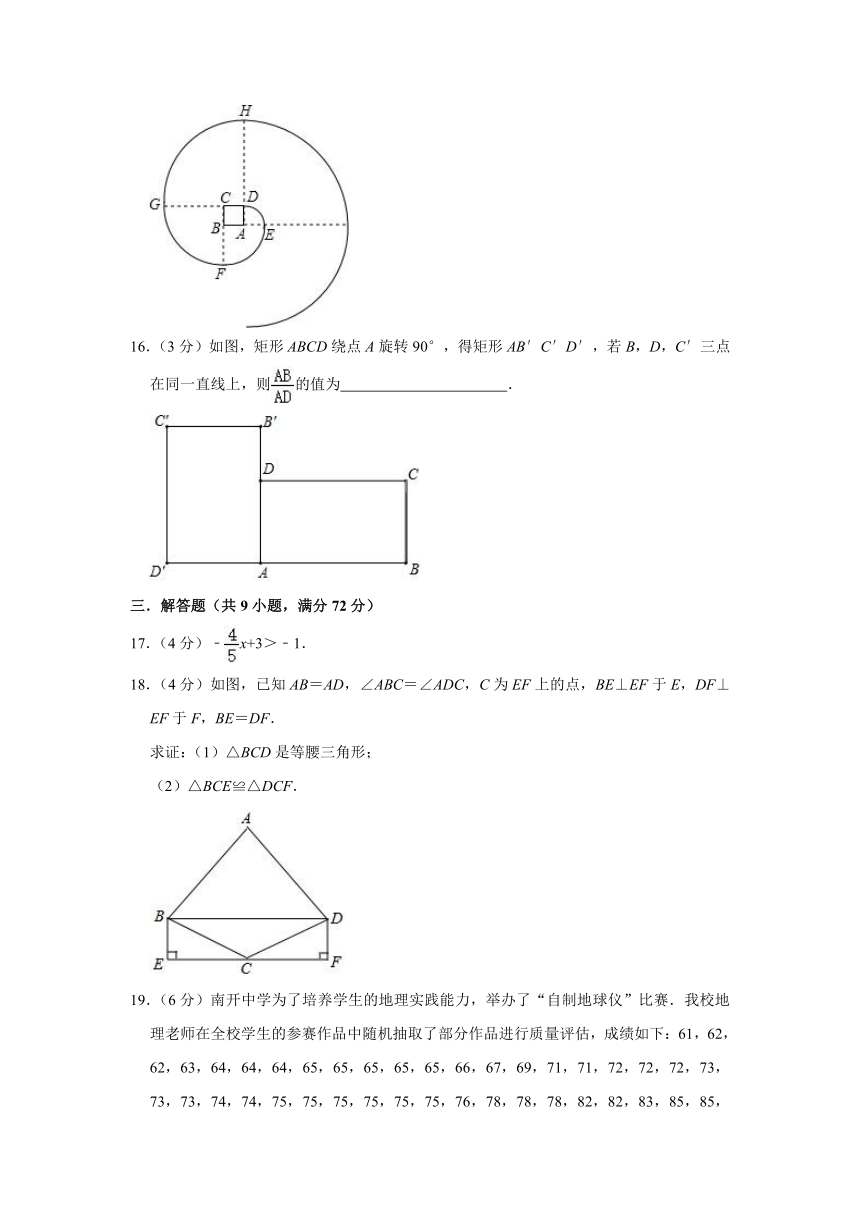
16.(3分)如图,矩形ABCD绕点A旋转90°,得矩形AB′C′D′,若B,D,C′三点在同一直线上,则的值为 .
三.解答题(共9小题,满分72分)
17.(4分)﹣x+3>﹣1.
18.(4分)如图,已知AB=AD,∠ABC=∠ADC,C为EF上的点,BE⊥EF于E,DF⊥EF于F,BE=DF.
求证:(1)△BCD是等腰三角形;
(2)△BCE≌△DCF.
19.(6分)南开中学为了培养学生的地理实践能力,举办了“自制地球仪”比赛.我校地理老师在全校学生的参赛作品中随机抽取了部分作品进行质量评估,成绩如下:61,62,62,63,64,64,64,65,65,65,65,65,66,67,69,71,71,72,72,72,73,73,73,74,74,75,75,75,75,75,75,76,78,78,78,82,82,83,85,85,85,87,87,88,88,291,92,95,97,98,并将成绩统计后绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
分数x 频数(人) 频率
60≤x<70 15 0.3
70≤x<80 a
80≤x<90 b
90≤x≤100 5
合计 c 1
(1)频数分布表中,a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)本次比赛学校共收到参赛作品900件,若80分以上(含80分)的作品将被展出,试估计全校将展出的作品数量.
20.(6分)已知,在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.小华准备画出此函数图象,列表如下:
35 … 1 2 3 4 …
y … 6 3 2 1.5 …
(1)根据小华的列表直接写出y关于x的函数关系式,x的取值范围是 ;
(2)请你在如图所示的坐标系中帮助他描点并连线,画出此函数图象;
(3)如果M(x1,y1),N(x2,y2)是此函数图象上的两个点,且x1>x2>0,判断y1与y2的大小.
21.(8分)关于x的一元二次方程x2+mx+m﹣3=0.
(1)若方程的一个根为1,求m的值;
(2)求证:方程总有两个不相等的实数根.
22.(10分)如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.
(1)尺规作图:过点O作AC的垂线,交劣弧于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求点O到AC的距离及sin∠ACD的值.
23.(10分)在数学活动课上,老师带领学生测量校园中一棵树的高度.如图,在树前的平地上选择一点C,测得树的顶端A的仰角为30°,在C,B间选择一点D(C,D,B三点在同一直线上),测得树的顶端A的仰角为75°,CD间距离为20m,求这棵树AB的高度.(结果保留根号).
24.(12分)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴的负半轴交于点C,且A(1,0),sin∠OBC=.过点B作线段BC的垂线交抛物线于点D,交y轴于点E.设直线x=﹣2与直线BD相交于点M,与x轴交于点N.
(1)求该抛物线的表达式;
(2)试判断以点A为圆心,AD长为半径的圆与y轴的位置关系,并给出证明;
(3)如图2,作直线OM.问:在(2)中的⊙A上是否存在一点P,使△OPM的面积最大?若存在,求出△OPM面积的最大值;若不存在,请说明理由.
25.(12分)【操作与发现】
如图①,在正方形ABCD中,点N,M分别在边BC、CD上.连接AM、AN、MN.∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而可得:DM+BN=MN.
(1)【实践探究】在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是 .
(2)如图②,在正方形ABCD中,点M、N分别在边DC、BC上,连接AM、AN、MN,∠MAN=45°,若tan∠BAN=,求证:M是CD的中点.
(3)【拓展】如图③,在矩形ABCD中,AB=12,AD=16,点M、N分别在边DC、BC上,连接AM、AN,已知∠MAN=45°,BN=4,则DM的长是 .
参考答案
1.A
2.B
3.C
4.B
5.D
6.C
7.C
8.A
9.C
10.C
11.变大.
12. m(m﹣4).
13. 75°.
14. 2.
15. 5π.
16. .
17. 去分母,得﹣4x+15>﹣5,
移项得﹣4x>﹣5﹣15,
合并,得:﹣4x>﹣20,
解得x<5.
18. 证明:(1)∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
即∠CBD=∠CDB,
∴BC=DC,
∴△BCD是等腰三角形;
(2)∵BE⊥EF于E,DF⊥EF于F,
∴∠E=∠F=90°,
在Rt△BCE和Rt△DCF中,
,
∴Rt△BCE≌Rt△DCF(HL).
19. (1)分别统计各组的频数可得,70≤x<80的频数为20,80≤x<90的频数为10,
因此a=20÷50=0.4,b=10,c=15+20+10+5=50,
故答案为:0.4,10,50,
(2)补全频数分布直方图如图所示:
(3)900×=270(人),
答:全校将展出的作品数量为270件.
20. (1)根据题意得,xy=3,
∴y关于x的函数关系式为y=,
∵△ABC中,BC边的长为x,
∴x的取值范围是x>0.
故答案为:x>0;
(2)描点,画出函数的图象,如图所示,
(3)∵反比例函数y=中,k=6>0,
∴当x>0时,y随x的增大而减小,
∵M(x1,y1),N(x2,y2)是函数y=图象上的两个点,
∴当x1>x2>0时,则0<y1<y2.
21. ∵方程的一个根为1,
∴1+m+m﹣3=0,
∴m=1;
(2)证明:∵a=1,b=m,c=m﹣3,
∴Δ=b2﹣4ac=m2﹣4(m﹣3)=m2﹣4m+12=(m﹣2)2+8>0,
∴方程总有两个不相等的实数根.
22. (1)分别以A、C为圆心,大于AC为半径画弧,在AC的两侧分别相交于P、Q两点,画直线PQ交劣弧于点D,交AC于点E,即作线段AC的垂直平分线,由垂径定理可知,直线PQ一定过点O;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,且AC=8,BC=6.
∴AB==10,
∵OD⊥AC,
∴AE=CE=AC=4,
又∵OA=OB,
∴OE是△ABC的中位线,
∴OE=BC=3,
由于PQ过圆心O,且PQ⊥AC,
即点O到AC的距离为3,
连接OC,在Rt△CDE中,
∵DE=OD﹣CE=5﹣3=2,CE=4,
∴CD===2
∴sin∠ACD===.
23. 如图,作DE⊥AC,垂足为E,
在Rt△CED中,
∵sinC=,∠C=30°,CD=20m,
∴DE=10m.
∵cosC=,
∴.
∴CE=10(m).
∵∠ADB是△ACD的外角,
∠ADB=75°,∠C=30°,
∴∠CAD=45°.
在Rt△ADE中,
∵tan∠EAD=,
∴AE=10m.
∴AC=AE+CE=(10+10)m.
在Rt△ABC中,∵sin∠C=,
∴AB=(5+5)m.
答:这棵树AB的高度是(5+5)m.
24. (1)∵y=ax2+bx﹣3,
∴OC=3.
∵sin∠OBC=,
∴∠OBC=45°.
∴OB=OC=3.
∴B(3,0).
∵A(1,0),
∴,
∴.
∴y=﹣x2+4x﹣3.
(2)相交.
证明:∵BD⊥BC,
∴∠OBE=45°.
∴OE=OB=3.
∴E(0,3 ).
设直线BE为y=kx+t,
∴.
∴,
∴y=﹣x+3,
联立.
解得,.
∴D(2,1).
∴AD==,
∵AD>OA,
∴以点A为圆心,AD长为半径的圆与y轴相交.
(3)存在,
如图,过A点作OM的垂线交⊙A于第一象限内点P,垂足为H.此时,△OPM的面积最大.
由,得.
∴M(﹣2,5).
OM=,
∵∠ONM=∠OHA=90°,∠MON=∠AOH,
∴△ONM∽△OHA.
∴.
∴AH=.
∵AP=,
∴PH=+,
∴S△OPM=OM PH=××(+)=.
25. (1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转的性质得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°﹣45°=45°,
∴∠MAN=∠EAN,
在△AMN和△AEN中,
,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵EN=BE+BN=DM+BN,
∴MN=BN+DM,
在Rt△CMN中,由勾股定理得:MN===10,
则BN+DM=10,
设正方形ABCD的边长为x,则BN=BC﹣CN=x﹣6,DM=CD﹣CM=x﹣8,
∴x﹣6+x﹣8=10,
解得:x=12,
即正方形ABCD的边长是12;
故答案为:12;
(2)证明:设BN=m,DM=n,
由(1)可知,MN=BN+DM=m+n,
∵∠B=90°,tan∠BAN=,
∴tan∠BAN==,
∴AB=3BN=3m,
∴CN=BC﹣BN=2m,CM=CD﹣DM=3m﹣n,
在Rt△CMN中,由勾股定理得:(2m)2+(3m﹣n)2=(m+n)2,
整理得:3m=2n,
∴CM=2n﹣n=n,
∴DM=CM,
即M是CD的中点;
(3)解:延长AB至P,使BP=BN=4,过P作BC的平行线交DC的延长线于Q,延长AN交PQ于E,连接EM,如图③所示:
则四边形APQD是正方形,
∴PQ=DQ=AP=AB+BP=12+4=16,
设DM=a,则MQ=16﹣a,
∵PQ∥BC,
∴△ABN∽△APE,
∴===,
∴PE=BN=,
∴EQ=PQ﹣PE=16﹣=,
由(1)得:EM=PE+DM=+a,
在Rt△QEM中,由勾股定理得:()2+(16﹣a)2=(+a)2,
解得:a=8,
即DM的长是8;
故答案为:8.
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)一个长方体礼盒的展开图如图所示(重叠部分不计)则该长方体的表面积为( )
A.34 B.36 C.42 D.46
2.(3分)云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列的云纹图案中,是中心对称图形的是( )
A. B.
C. D.
3.(3分)若代数式有意义,则x的取值范围是( )
A.x≥2 B.x≥0 C.x≥0且x≠2 D.x≠2
4.(3分)若一个正比例函数的图象经过点A(1,﹣2),B(m,4)两点,则m的值为( )
A.2 B.﹣2 C.8 D.﹣8
5.(3分)下列计算正确的是( )
A. B.
C. D.
6.(3分)实数a,b,c在数轴上的对应点的位置如图所示,如果a+b=0,那么下列结论正确的是( )
A.> B.a+c<0 C.abc<0 D.
7.(3分)在一次联欢晚会上,某班进行以下游戏,准备两个不透明的袋子和7个小球(大小、形状完全一样),一个袋子里放置3个小球,球面上分别写着“好”“运”“来”,另一个袋子里放置4个小球,球面上分别写着“新”“年”“好”“运”.现从两个袋子里各随机抽取一个球,球面上的字可以组成“好运”字样的获得一等奖,则获得一等奖的概率为( )
A. B. C. D.
8.(3分)如图,一次函数y1=x与二次函数图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( )
A. B.
C. D.
9.(3分)已知四边形ABCD是平行四边形,则下列结论中正确的是( )
A.当AB⊥BD时,它是菱形
B.当AC=BD时,它是正方形
C.当∠ABC=90°时,它是矩形
D.当AB=BC时,它是矩形
10.(3分)如图,矩形ABCD中AB是3cm,BC是2cm,一个边长为1cm的小正方形沿着矩形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形箭头的方向是( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)某工程队有14名员工,他们的工种及相应每人每月工资如下表所示:
工种 电工 木工 瓦工
人数 5 4 5
每人每月工资(元) 7000 6000 5000
现该工程队进行了人员调整:减少木工2名,增加电工、瓦工各1名,与调整前相比,该工程队员工月工资的方差 (填“变小”“不变”或“变大”).
12.(3分)因式分解:m2﹣4m= .
13.(3分)如图,在 ABCD中,以点D为圆心,以DA的长为半径画弧交边BC于点E,连接AE,若∠ADE=30°,则∠AEB= .
14.(3分)方程的解为 .
15.(3分)如图,四边形ABCD是正方形,曲线DEFGH…叫做“正方形的渐开线“,其中,,,,…依次连接,它们的圆心依次按A、B、C、D循环.当AB=1时,曲线DEFGH的长度是 .
16.(3分)如图,矩形ABCD绕点A旋转90°,得矩形AB′C′D′,若B,D,C′三点在同一直线上,则的值为 .
三.解答题(共9小题,满分72分)
17.(4分)﹣x+3>﹣1.
18.(4分)如图,已知AB=AD,∠ABC=∠ADC,C为EF上的点,BE⊥EF于E,DF⊥EF于F,BE=DF.
求证:(1)△BCD是等腰三角形;
(2)△BCE≌△DCF.
19.(6分)南开中学为了培养学生的地理实践能力,举办了“自制地球仪”比赛.我校地理老师在全校学生的参赛作品中随机抽取了部分作品进行质量评估,成绩如下:61,62,62,63,64,64,64,65,65,65,65,65,66,67,69,71,71,72,72,72,73,73,73,74,74,75,75,75,75,75,75,76,78,78,78,82,82,83,85,85,85,87,87,88,88,291,92,95,97,98,并将成绩统计后绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
分数x 频数(人) 频率
60≤x<70 15 0.3
70≤x<80 a
80≤x<90 b
90≤x≤100 5
合计 c 1
(1)频数分布表中,a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)本次比赛学校共收到参赛作品900件,若80分以上(含80分)的作品将被展出,试估计全校将展出的作品数量.
20.(6分)已知,在△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.小华准备画出此函数图象,列表如下:
35 … 1 2 3 4 …
y … 6 3 2 1.5 …
(1)根据小华的列表直接写出y关于x的函数关系式,x的取值范围是 ;
(2)请你在如图所示的坐标系中帮助他描点并连线,画出此函数图象;
(3)如果M(x1,y1),N(x2,y2)是此函数图象上的两个点,且x1>x2>0,判断y1与y2的大小.
21.(8分)关于x的一元二次方程x2+mx+m﹣3=0.
(1)若方程的一个根为1,求m的值;
(2)求证:方程总有两个不相等的实数根.
22.(10分)如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.
(1)尺规作图:过点O作AC的垂线,交劣弧于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求点O到AC的距离及sin∠ACD的值.
23.(10分)在数学活动课上,老师带领学生测量校园中一棵树的高度.如图,在树前的平地上选择一点C,测得树的顶端A的仰角为30°,在C,B间选择一点D(C,D,B三点在同一直线上),测得树的顶端A的仰角为75°,CD间距离为20m,求这棵树AB的高度.(结果保留根号).
24.(12分)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴的负半轴交于点C,且A(1,0),sin∠OBC=.过点B作线段BC的垂线交抛物线于点D,交y轴于点E.设直线x=﹣2与直线BD相交于点M,与x轴交于点N.
(1)求该抛物线的表达式;
(2)试判断以点A为圆心,AD长为半径的圆与y轴的位置关系,并给出证明;
(3)如图2,作直线OM.问:在(2)中的⊙A上是否存在一点P,使△OPM的面积最大?若存在,求出△OPM面积的最大值;若不存在,请说明理由.
25.(12分)【操作与发现】
如图①,在正方形ABCD中,点N,M分别在边BC、CD上.连接AM、AN、MN.∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而可得:DM+BN=MN.
(1)【实践探究】在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是 .
(2)如图②,在正方形ABCD中,点M、N分别在边DC、BC上,连接AM、AN、MN,∠MAN=45°,若tan∠BAN=,求证:M是CD的中点.
(3)【拓展】如图③,在矩形ABCD中,AB=12,AD=16,点M、N分别在边DC、BC上,连接AM、AN,已知∠MAN=45°,BN=4,则DM的长是 .
参考答案
1.A
2.B
3.C
4.B
5.D
6.C
7.C
8.A
9.C
10.C
11.变大.
12. m(m﹣4).
13. 75°.
14. 2.
15. 5π.
16. .
17. 去分母,得﹣4x+15>﹣5,
移项得﹣4x>﹣5﹣15,
合并,得:﹣4x>﹣20,
解得x<5.
18. 证明:(1)∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
即∠CBD=∠CDB,
∴BC=DC,
∴△BCD是等腰三角形;
(2)∵BE⊥EF于E,DF⊥EF于F,
∴∠E=∠F=90°,
在Rt△BCE和Rt△DCF中,
,
∴Rt△BCE≌Rt△DCF(HL).
19. (1)分别统计各组的频数可得,70≤x<80的频数为20,80≤x<90的频数为10,
因此a=20÷50=0.4,b=10,c=15+20+10+5=50,
故答案为:0.4,10,50,
(2)补全频数分布直方图如图所示:
(3)900×=270(人),
答:全校将展出的作品数量为270件.
20. (1)根据题意得,xy=3,
∴y关于x的函数关系式为y=,
∵△ABC中,BC边的长为x,
∴x的取值范围是x>0.
故答案为:x>0;
(2)描点,画出函数的图象,如图所示,
(3)∵反比例函数y=中,k=6>0,
∴当x>0时,y随x的增大而减小,
∵M(x1,y1),N(x2,y2)是函数y=图象上的两个点,
∴当x1>x2>0时,则0<y1<y2.
21. ∵方程的一个根为1,
∴1+m+m﹣3=0,
∴m=1;
(2)证明:∵a=1,b=m,c=m﹣3,
∴Δ=b2﹣4ac=m2﹣4(m﹣3)=m2﹣4m+12=(m﹣2)2+8>0,
∴方程总有两个不相等的实数根.
22. (1)分别以A、C为圆心,大于AC为半径画弧,在AC的两侧分别相交于P、Q两点,画直线PQ交劣弧于点D,交AC于点E,即作线段AC的垂直平分线,由垂径定理可知,直线PQ一定过点O;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,且AC=8,BC=6.
∴AB==10,
∵OD⊥AC,
∴AE=CE=AC=4,
又∵OA=OB,
∴OE是△ABC的中位线,
∴OE=BC=3,
由于PQ过圆心O,且PQ⊥AC,
即点O到AC的距离为3,
连接OC,在Rt△CDE中,
∵DE=OD﹣CE=5﹣3=2,CE=4,
∴CD===2
∴sin∠ACD===.
23. 如图,作DE⊥AC,垂足为E,
在Rt△CED中,
∵sinC=,∠C=30°,CD=20m,
∴DE=10m.
∵cosC=,
∴.
∴CE=10(m).
∵∠ADB是△ACD的外角,
∠ADB=75°,∠C=30°,
∴∠CAD=45°.
在Rt△ADE中,
∵tan∠EAD=,
∴AE=10m.
∴AC=AE+CE=(10+10)m.
在Rt△ABC中,∵sin∠C=,
∴AB=(5+5)m.
答:这棵树AB的高度是(5+5)m.
24. (1)∵y=ax2+bx﹣3,
∴OC=3.
∵sin∠OBC=,
∴∠OBC=45°.
∴OB=OC=3.
∴B(3,0).
∵A(1,0),
∴,
∴.
∴y=﹣x2+4x﹣3.
(2)相交.
证明:∵BD⊥BC,
∴∠OBE=45°.
∴OE=OB=3.
∴E(0,3 ).
设直线BE为y=kx+t,
∴.
∴,
∴y=﹣x+3,
联立.
解得,.
∴D(2,1).
∴AD==,
∵AD>OA,
∴以点A为圆心,AD长为半径的圆与y轴相交.
(3)存在,
如图,过A点作OM的垂线交⊙A于第一象限内点P,垂足为H.此时,△OPM的面积最大.
由,得.
∴M(﹣2,5).
OM=,
∵∠ONM=∠OHA=90°,∠MON=∠AOH,
∴△ONM∽△OHA.
∴.
∴AH=.
∵AP=,
∴PH=+,
∴S△OPM=OM PH=××(+)=.
25. (1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转的性质得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°﹣45°=45°,
∴∠MAN=∠EAN,
在△AMN和△AEN中,
,
∴△AMN≌△AEN(SAS),
∴MN=EN,
∵EN=BE+BN=DM+BN,
∴MN=BN+DM,
在Rt△CMN中,由勾股定理得:MN===10,
则BN+DM=10,
设正方形ABCD的边长为x,则BN=BC﹣CN=x﹣6,DM=CD﹣CM=x﹣8,
∴x﹣6+x﹣8=10,
解得:x=12,
即正方形ABCD的边长是12;
故答案为:12;
(2)证明:设BN=m,DM=n,
由(1)可知,MN=BN+DM=m+n,
∵∠B=90°,tan∠BAN=,
∴tan∠BAN==,
∴AB=3BN=3m,
∴CN=BC﹣BN=2m,CM=CD﹣DM=3m﹣n,
在Rt△CMN中,由勾股定理得:(2m)2+(3m﹣n)2=(m+n)2,
整理得:3m=2n,
∴CM=2n﹣n=n,
∴DM=CM,
即M是CD的中点;
(3)解:延长AB至P,使BP=BN=4,过P作BC的平行线交DC的延长线于Q,延长AN交PQ于E,连接EM,如图③所示:
则四边形APQD是正方形,
∴PQ=DQ=AP=AB+BP=12+4=16,
设DM=a,则MQ=16﹣a,
∵PQ∥BC,
∴△ABN∽△APE,
∴===,
∴PE=BN=,
∴EQ=PQ﹣PE=16﹣=,
由(1)得:EM=PE+DM=+a,
在Rt△QEM中,由勾股定理得:()2+(16﹣a)2=(+a)2,
解得:a=8,
即DM的长是8;
故答案为:8.
同课章节目录
