2.2.1 倾斜角与斜率 教案
文档属性
| 名称 | 2.2.1 倾斜角与斜率 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 00:00:00 | ||
图片预览

文档简介
2.1.1 倾斜角与斜率
【教学目标】
1、探索确定直线位置的几何要素,感受倾斜角这个反映倾斜程度的几何量的形成过程。
2、通过教学,使学生从生活中的坡度,自然迁移到数学中直线的斜率,感受数学概念来源于生活实际,数学概念的形成是自然的,从而渗透辩证唯物主义思想。
3、充分利用倾斜角和斜率是从数与形两方面,刻画直线相对于x轴倾斜程度的两个量这一事实,渗透数形结合思想。
4、经历用代数方法刻画直线斜率的过程,初步掌握过已知两点的直线的斜率计算公式,渗透几何问题代数化的解析几何研究思想。。
【教学重难点】
重点:倾斜角、斜率、过两点的直线的斜率公式;
难点:斜率。
【教学过程】
(一)新知引入
1.综合法与坐标法;
2.解析几何相关内容介绍;
3.本章前半部分的内容介绍。
(二)新课讲授
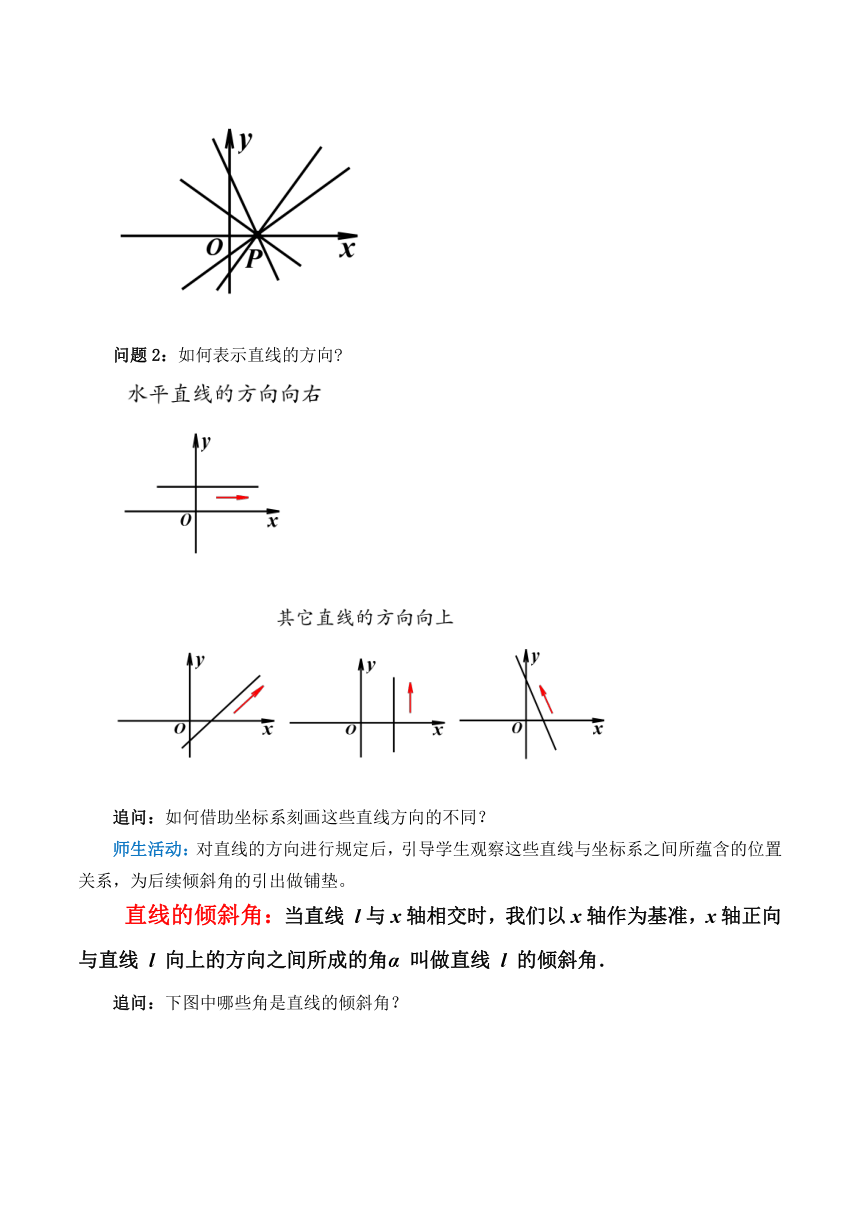
问题1:确定一条直线的几何要素是什么 对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置
师生活动:学生独立思考后回答,教师总结:一点+一个方向。
追问:观察以下的直线,它们有何区别?
问题2:如何表示直线的方向
追问:如何借助坐标系刻画这些直线方向的不同?
师生活动:对直线的方向进行规定后,引导学生观察这些直线与坐标系之间所蕴含的位置关系,为后续倾斜角的引出做铺垫。
直线的倾斜角:当直线 l与x轴相交时,我们以x轴作为基准,x轴正向与直线 l 向上的方向之间所成的角α 叫做直线 l 的倾斜角.
追问:下图中哪些角是直线的倾斜角?
问题3:直线的倾斜角的范围是什么?
师生活动:通过两个问题,加强学生对直线的倾斜角这一概念的理解,并指出:任何一条直线都有一个倾斜角与之对应,直线的方向不同,直线的倾斜程度不同,倾斜角也不相等。
问题4:直线l的倾斜角α与两点的坐标有什么内在联系?
:在平面直角坐标系中,设l直线的倾斜角为α .
(1)已知直线l经过O(0,0), P(,1) ,α与O, P的坐标有什么关系?
(2)类似地,若直线l经过, (,0) ,α与, 的坐标又有什么关系?
(3)一般地,若直线l经过, (, )(≠ ) ,那么α与, 的坐标有怎样的关系?
问题5:当直线与x轴平行(重合)或垂直时,上式还成立吗?
结论:直线的倾斜角α与直线上的两点P1(),的坐标有如下关系:
斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率. 斜率常用小写字母表示,即.
问题6:当直线的倾斜角由0°逐渐增大到180°时,其斜率如何变化?为什么?
师生活动:通过以上探究过程,利用向量法及正切函数的定义引入直线方向的第二种刻画方法——斜率。进一步借助正切函数的图象研究斜率在不同的倾斜角范围内的取值特点,并在此基础上说明“坡度”与斜率的区别与联系。
问题7:直线的方向向量与斜率 有什么关系?
结论1 若直线的斜率为,它的一个方向向量的坐标为(),则.
结论2 若直线的斜率为,则它的一个方向向量的坐标为(1, ).
小结:
(三)例题分析
例1 如图,已知A(3,2),B(,1),C(0,1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
分析:两点坐标——斜率——倾斜角。
师生活动:学生思考后自主解答,学生代表板演,教师纠正指导。
(四)归纳小结
(五)作业布置
1.完成课本55页的练习题3、4、5;
2.完成《新课程同步练习册》本节的习题。
【教学目标】
1、探索确定直线位置的几何要素,感受倾斜角这个反映倾斜程度的几何量的形成过程。
2、通过教学,使学生从生活中的坡度,自然迁移到数学中直线的斜率,感受数学概念来源于生活实际,数学概念的形成是自然的,从而渗透辩证唯物主义思想。
3、充分利用倾斜角和斜率是从数与形两方面,刻画直线相对于x轴倾斜程度的两个量这一事实,渗透数形结合思想。
4、经历用代数方法刻画直线斜率的过程,初步掌握过已知两点的直线的斜率计算公式,渗透几何问题代数化的解析几何研究思想。。
【教学重难点】
重点:倾斜角、斜率、过两点的直线的斜率公式;
难点:斜率。
【教学过程】
(一)新知引入
1.综合法与坐标法;
2.解析几何相关内容介绍;
3.本章前半部分的内容介绍。
(二)新课讲授
问题1:确定一条直线的几何要素是什么 对于平面直角坐标系中的一条直线l,如何利用坐标系确定它的位置
师生活动:学生独立思考后回答,教师总结:一点+一个方向。
追问:观察以下的直线,它们有何区别?
问题2:如何表示直线的方向
追问:如何借助坐标系刻画这些直线方向的不同?
师生活动:对直线的方向进行规定后,引导学生观察这些直线与坐标系之间所蕴含的位置关系,为后续倾斜角的引出做铺垫。
直线的倾斜角:当直线 l与x轴相交时,我们以x轴作为基准,x轴正向与直线 l 向上的方向之间所成的角α 叫做直线 l 的倾斜角.
追问:下图中哪些角是直线的倾斜角?
问题3:直线的倾斜角的范围是什么?
师生活动:通过两个问题,加强学生对直线的倾斜角这一概念的理解,并指出:任何一条直线都有一个倾斜角与之对应,直线的方向不同,直线的倾斜程度不同,倾斜角也不相等。
问题4:直线l的倾斜角α与两点的坐标有什么内在联系?
:在平面直角坐标系中,设l直线的倾斜角为α .
(1)已知直线l经过O(0,0), P(,1) ,α与O, P的坐标有什么关系?
(2)类似地,若直线l经过, (,0) ,α与, 的坐标又有什么关系?
(3)一般地,若直线l经过, (, )(≠ ) ,那么α与, 的坐标有怎样的关系?
问题5:当直线与x轴平行(重合)或垂直时,上式还成立吗?
结论:直线的倾斜角α与直线上的两点P1(),的坐标有如下关系:
斜率:我们把一条直线的倾斜角α的正切值叫做这条直线的斜率. 斜率常用小写字母表示,即.
问题6:当直线的倾斜角由0°逐渐增大到180°时,其斜率如何变化?为什么?
师生活动:通过以上探究过程,利用向量法及正切函数的定义引入直线方向的第二种刻画方法——斜率。进一步借助正切函数的图象研究斜率在不同的倾斜角范围内的取值特点,并在此基础上说明“坡度”与斜率的区别与联系。
问题7:直线的方向向量与斜率 有什么关系?
结论1 若直线的斜率为,它的一个方向向量的坐标为(),则.
结论2 若直线的斜率为,则它的一个方向向量的坐标为(1, ).
小结:
(三)例题分析
例1 如图,已知A(3,2),B(,1),C(0,1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
分析:两点坐标——斜率——倾斜角。
师生活动:学生思考后自主解答,学生代表板演,教师纠正指导。
(四)归纳小结
(五)作业布置
1.完成课本55页的练习题3、4、5;
2.完成《新课程同步练习册》本节的习题。
