7.3.2第2课时 正弦函数、余弦函数的性质(2) 学案(无答案)
文档属性
| 名称 | 7.3.2第2课时 正弦函数、余弦函数的性质(2) 学案(无答案) | 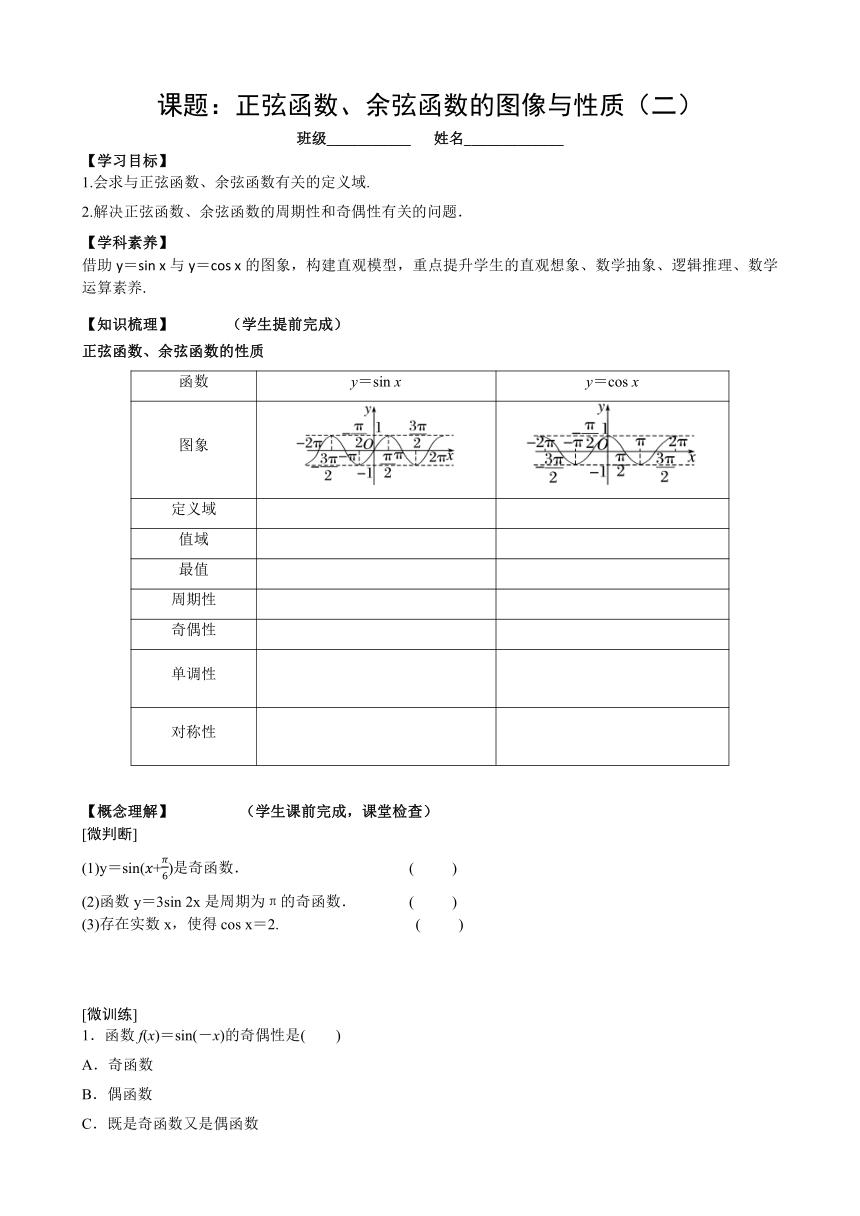 | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 23:32:34 | ||
图片预览

文档简介
课题:正弦函数、余弦函数的图像与性质(二)
班级___________ 姓名_____________
【学习目标】
1.会求与正弦函数、余弦函数有关的定义域.
2.解决正弦函数、余弦函数的周期性和奇偶性有关的问题.
【学科素养】
借助y=sin x与y=cos x的图象,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
【知识梳理】 (学生提前完成)
正弦函数、余弦函数的性质
函数 y=sin x y=cos x
图象
定义域
值域
最值
周期性
奇偶性
单调性
对称性
【概念理解】 (学生课前完成,课堂检查)
[微判断]
(1)y=sin( +)是奇函数. ( )
(2)函数y=3sin 2x是周期为π的奇函数. ( )
(3)存在实数x,使得cos x=2. ( )
[微训练]
1.函数f(x)=sin(-x)的奇偶性是( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数
2.(多选)下列函数中周期为π,且为偶函数的是( )
A.y=|sin x| B.y=sin 2x
C.y=sin D.y=cos x
【例题精讲】 (师生共讨)
题型一 正弦函数、余弦函数图象的应用
【例1】方程2sin x-1=0,x∈[0,2π]的解集为________.
【延伸探究】
1.不等式2sin x-1≥0,x∈[0,2π]的解集为( )
A. B. C. D.
2.在本例中把“x∈[0,2π]”改为“x∈R”,求不等式2sin x-1≥0的解集.
【迁移1】 (变换结论)利用正弦曲线,求满足【迁移2】 (变换结论)函数y=log2(2sin x+1)的定义域为________
【例2】求下列函数的最大值及取得最大值时自变量x的集合
y=cos ; (2)y=2-sin2 x
【变式】求下列函数的最大值及取得最大值时自变量x的集合
y=-2sinx;(2)y=2-cos
题型二 正、余弦函数的奇偶性与周期性
例2 定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.- B. C.- D.
【延伸探究】
1.在本例条件中,把“偶函数”变成“奇函数”,其他不变,则f 的值为________.
2.若本例中条件变为定义在R上的函数f(x)既是偶函数,又是周期函数,f =-f(x),f =1,则f 的值为________.
【当堂巩固】 课本: 练习 P212 3、4
【总结反思】
班级___________ 姓名_____________
【学习目标】
1.会求与正弦函数、余弦函数有关的定义域.
2.解决正弦函数、余弦函数的周期性和奇偶性有关的问题.
【学科素养】
借助y=sin x与y=cos x的图象,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
【知识梳理】 (学生提前完成)
正弦函数、余弦函数的性质
函数 y=sin x y=cos x
图象
定义域
值域
最值
周期性
奇偶性
单调性
对称性
【概念理解】 (学生课前完成,课堂检查)
[微判断]
(1)y=sin( +)是奇函数. ( )
(2)函数y=3sin 2x是周期为π的奇函数. ( )
(3)存在实数x,使得cos x=2. ( )
[微训练]
1.函数f(x)=sin(-x)的奇偶性是( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数
2.(多选)下列函数中周期为π,且为偶函数的是( )
A.y=|sin x| B.y=sin 2x
C.y=sin D.y=cos x
【例题精讲】 (师生共讨)
题型一 正弦函数、余弦函数图象的应用
【例1】方程2sin x-1=0,x∈[0,2π]的解集为________.
【延伸探究】
1.不等式2sin x-1≥0,x∈[0,2π]的解集为( )
A. B. C. D.
2.在本例中把“x∈[0,2π]”改为“x∈R”,求不等式2sin x-1≥0的解集.
【迁移1】 (变换结论)利用正弦曲线,求满足
【例2】求下列函数的最大值及取得最大值时自变量x的集合
y=cos ; (2)y=2-sin2 x
【变式】求下列函数的最大值及取得最大值时自变量x的集合
y=-2sinx;(2)y=2-cos
题型二 正、余弦函数的奇偶性与周期性
例2 定义在R上的函数f(x)既是偶函数,又是周期函数,若f(x)的最小正周期为π,且当x∈时,f(x)=sin x,则f 等于( )
A.- B. C.- D.
【延伸探究】
1.在本例条件中,把“偶函数”变成“奇函数”,其他不变,则f 的值为________.
2.若本例中条件变为定义在R上的函数f(x)既是偶函数,又是周期函数,f =-f(x),f =1,则f 的值为________.
【当堂巩固】 课本: 练习 P212 3、4
【总结反思】
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
