2023年广东省广州市中考数学模拟试卷(三)(含答案)
文档属性
| 名称 | 2023年广东省广州市中考数学模拟试卷(三)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 375.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 00:38:53 | ||
图片预览

文档简介
2023年广州市中考数学模拟试卷(三)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)如图是一个几何体水箱的表面展开图,根据图中标注的尺寸,则该几何体的表面积为( )
A.28π B.32π C.33π D.35π
2.(3分)下列图形中,是中心对称图形的是( )
A. B. C. D.
3.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣2 B.x≥﹣2,且x≠0 C.x>﹣2 D.x≤﹣2,且x≠0
4.(3分)点(3,﹣5)在正比例函数y=kx(k≠0)的图象上,则k的值为( )
A.﹣15 B.15 C.﹣ D.﹣
5.(3分)下列运算正确的是( )
A.﹣= B.=﹣3 C.=2 D.=+
6.(3分)如图,正方形的周长为8个单位,在该正方形的4个顶点处分别标上0、2、4、6,先让正方形上表示数字6的点与数轴上表示﹣3的点重合,再将数轴按顺时针方向环绕在该正方形上.则数轴上表示99的点与正方形上表示数字( )的点重合.
A.0 B.2 C.4 D.6
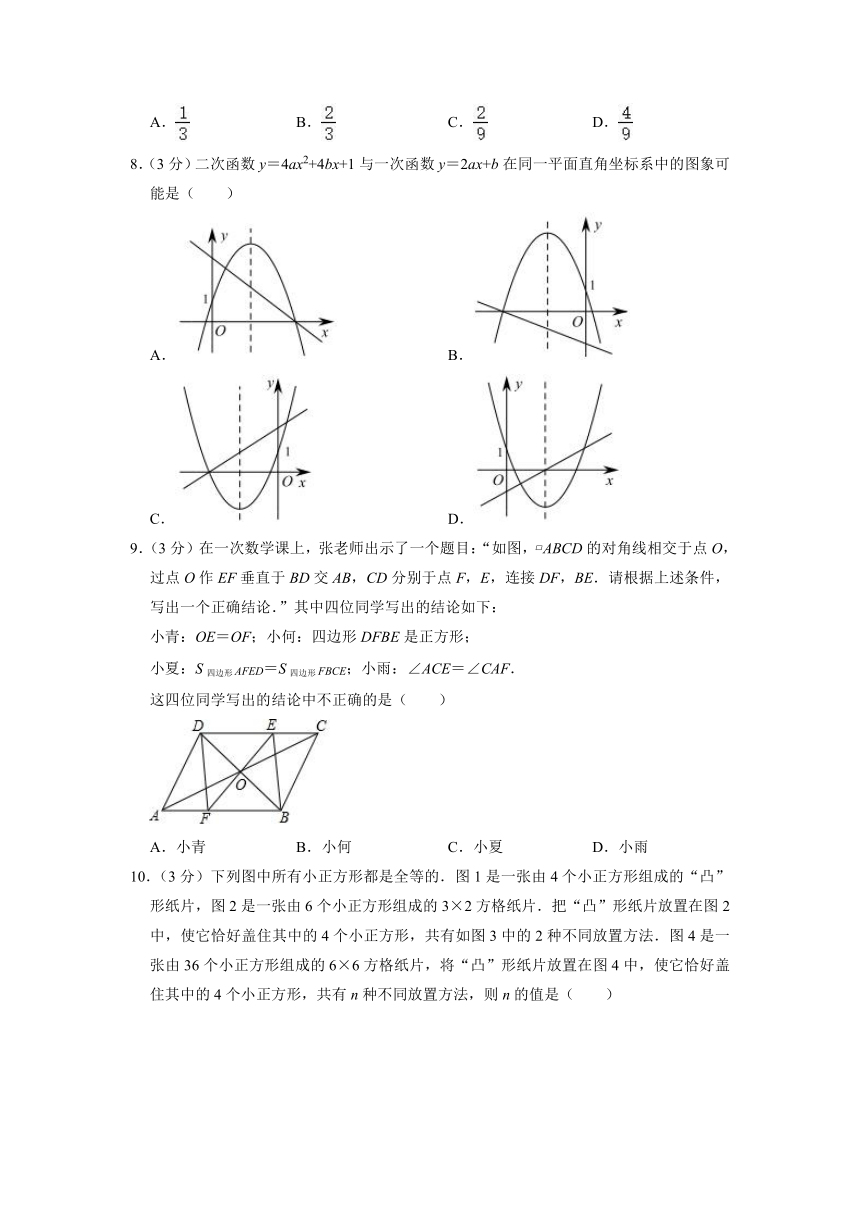
7.(3分)某校开展“文明小卫士”活动,从学生会的2名男生和1名女生中随机选取两名进行督查,恰好选中两名男生的概率是( )
A. B. C. D.
8.(3分)二次函数y=4ax2+4bx+1与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.(3分)在一次数学课上,张老师出示了一个题目:“如图, ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )
A.小青 B.小何 C.小夏 D.小雨
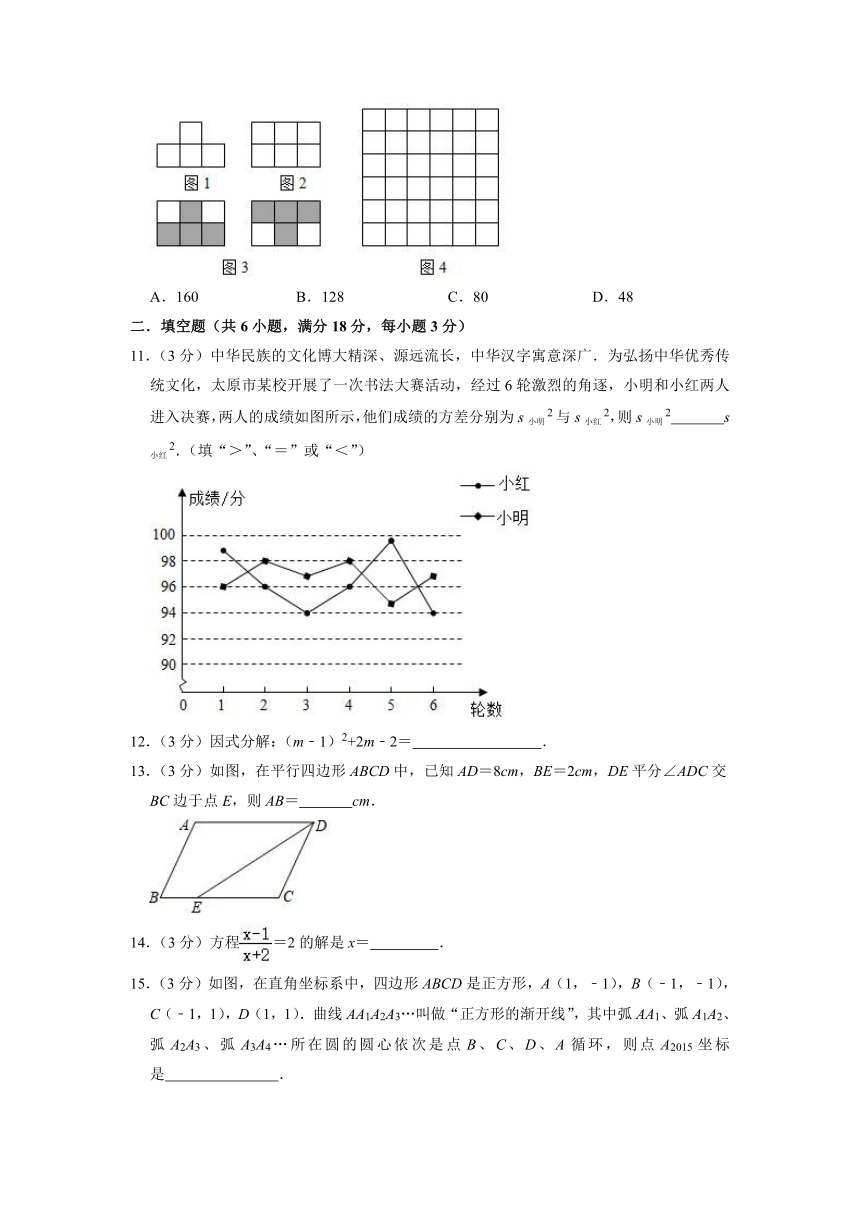
10.(3分)下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的“凸”形纸片,图2是一张由6个小正方形组成的3×2方格纸片.把“凸”形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的2种不同放置方法.图4是一张由36个小正方形组成的6×6方格纸片,将“凸”形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有n种不同放置方法,则n的值是( )
A.160 B.128 C.80 D.48
二.填空题(共6小题,满分18分,每小题3分)
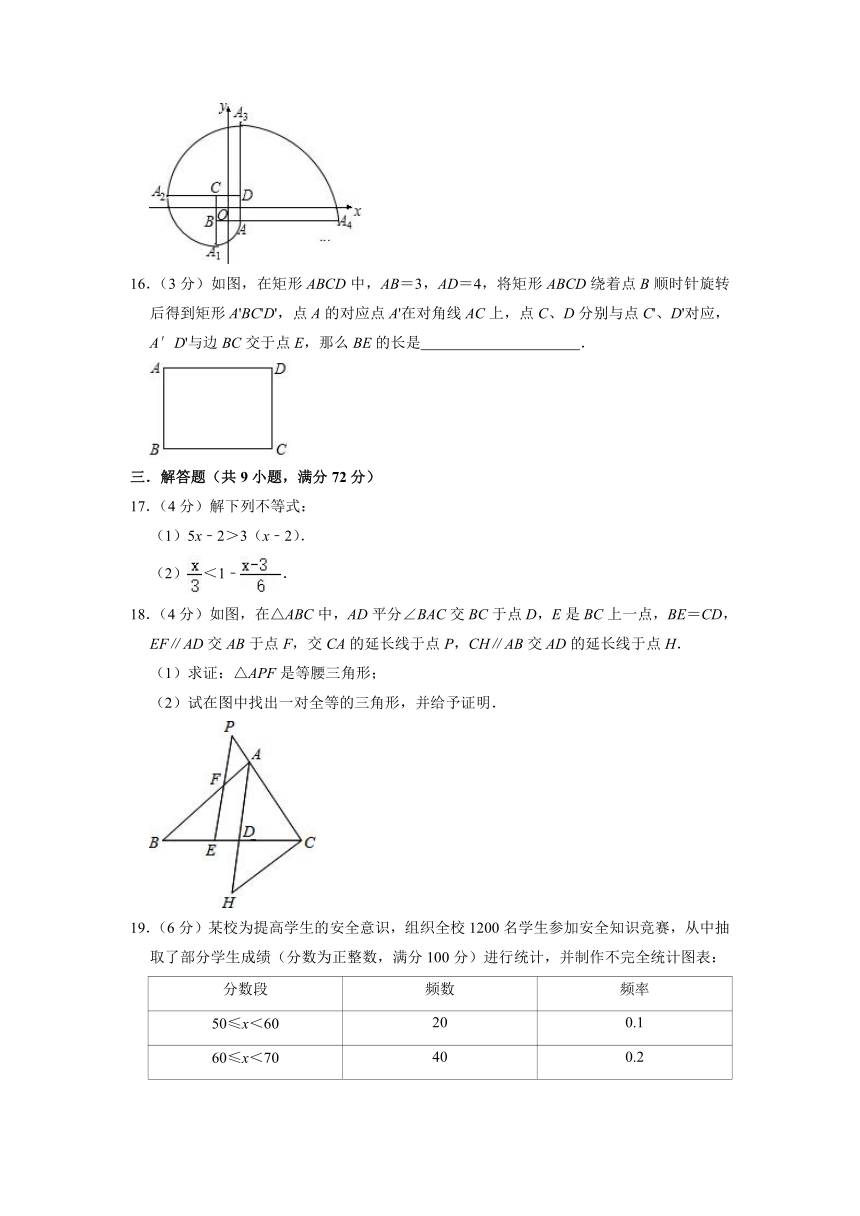
11.(3分)中华民族的文化博大精深、源远流长,中华汉字寓意深广.为弘扬中华优秀传统文化,太原市某校开展了一次书法大赛活动,经过6轮激烈的角逐,小明和小红两人进入决赛,两人的成绩如图所示,他们成绩的方差分别为s小明2与s小红2,则s小明2 s小红2.(填“>”、“=”或“<”)
12.(3分)因式分解:(m﹣1)2+2m﹣2= .
13.(3分)如图,在平行四边形ABCD中,已知AD=8cm,BE=2cm,DE平分∠ADC交BC边于点E,则AB= cm.
14.(3分)方程=2的解是x= .
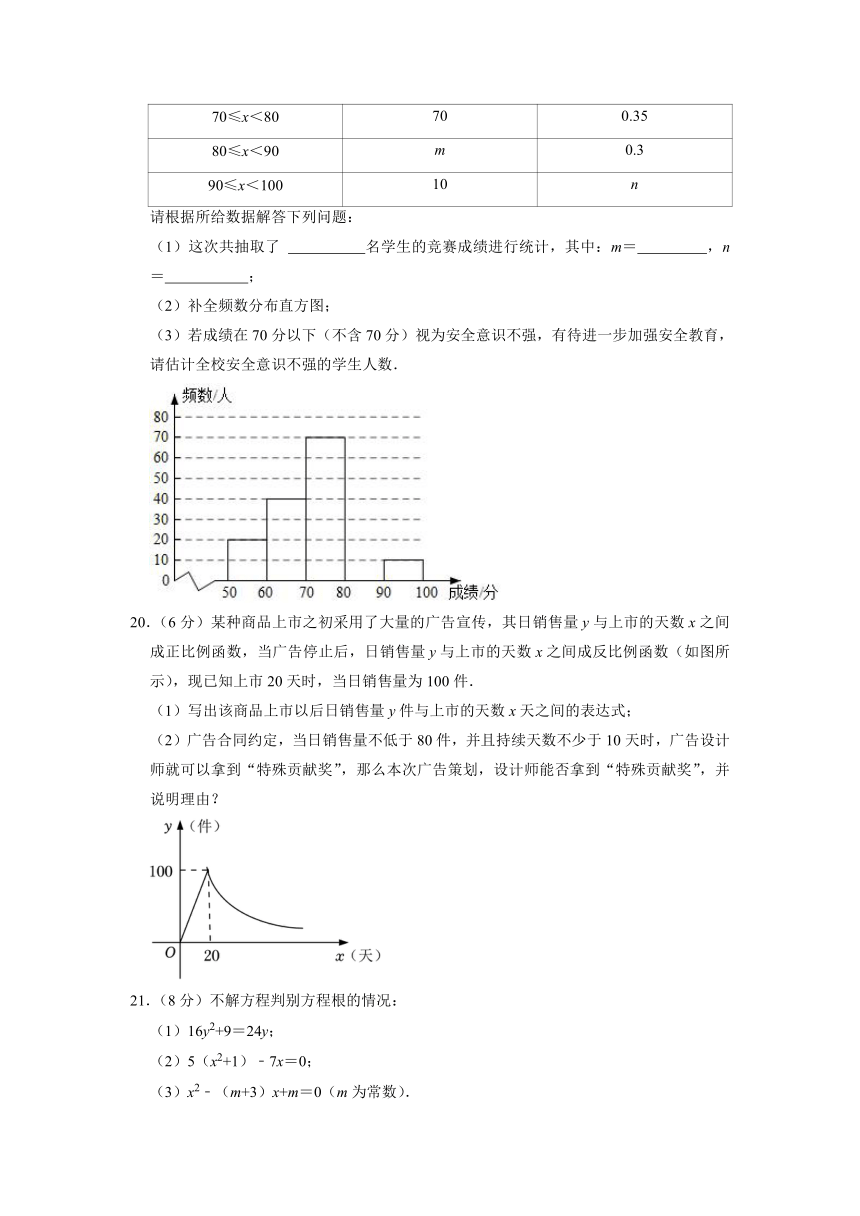
15.(3分)如图,在直角坐标系中,四边形ABCD是正方形,A(1,﹣1),B(﹣1,﹣1),C(﹣1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是 .
16.(3分)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是 .
三.解答题(共9小题,满分72分)
17.(4分)解下列不等式:
(1)5x﹣2>3(x﹣2).
(2)<1﹣.
18.(4分)如图,在△ABC中,AD平分∠BAC交BC于点D,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)试在图中找出一对全等的三角形,并给予证明.
19.(6分)某校为提高学生的安全意识,组织全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩(分数为正整数,满分100分)进行统计,并制作不完全统计图表:
分数段 频数 频率
50≤x<60 20 0.1
60≤x<70 40 0.2
70≤x<80 70 0.35
80≤x<90 m 0.3
90≤x<100 10 n
请根据所给数据解答下列问题:
(1)这次共抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(不含70分)视为安全意识不强,有待进一步加强安全教育,请估计全校安全意识不强的学生人数.
20.(6分)某种商品上市之初采用了大量的广告宣传,其日销售量y与上市的天数x之间成正比例函数,当广告停止后,日销售量y与上市的天数x之间成反比例函数(如图所示),现已知上市20天时,当日销售量为100件.
(1)写出该商品上市以后日销售量y件与上市的天数x天之间的表达式;
(2)广告合同约定,当日销售量不低于80件,并且持续天数不少于10天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”,并说明理由?
21.(8分)不解方程判别方程根的情况:
(1)16y2+9=24y;
(2)5(x2+1)﹣7x=0;
(3)x2﹣(m+3)x+m=0(m为常数).
22.(10分)如图,已知在△ABC中,AB=AC=6,BC=4,点E、F分别是AB、AC的中点,过点C作CD∥AB交EF的延长线于点D,联结AD.
(1)求∠B的正弦值;
(2)求线段AD的长.
23.(10分)如图,无人机在空中C处测得地面A、B两点的俯角分别为30°、45°,点A、B在同一水平地面上,如果测得A、B两点间的距离是15+15米.
求无人机与地面的垂直高度是多少米?
24.(12分)二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),直线l:x=m(m>3)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线l上找点P(点P在第一象限),使得以点P,D,B为顶点的三角形与以点A,C,O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在第一象限内的点Q,使得△BPQ是以P为直角顶点的等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
25.(12分)【问题情境】
(1)如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
【尝试应用】
(2)如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
【拓展提升】
(3)如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.
参考答案
1.B
2.D
3.B
4.D
5.A
6.C
7.A
8.D
9.B
10.C
11. <.
12. (m﹣1)(m+1).
13. 6.
14. ﹣5.
15. (1,4031).
16. .
17. (1)5x﹣2>3(x﹣2),
去括号得,5x﹣2>3x﹣6,
移项得,5x﹣3x>﹣6+2,
合并同类项得,2x>﹣4,
系数化为1得,x>﹣2;
(2)<1﹣,
去分母得,2x<6﹣(x﹣3),
去括号得,2x<6﹣x+3,
移项得,2x+x<6+3,
合并同类项得,3x<9,
系数化为1得,x<3.
18. (1)证明:如图.
∵EF∥AD,
∴∠1=∠4,∠2=∠P,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠4=∠P,
∴AF=AP,
即△APF是等腰三角形;
(2)解:△BEF≌△CDH.理由如下:
∵CH∥AB,
∴∠5=∠B,∠H=∠1,
∵EF∥AD,
∴∠1=∠3,
∴∠H=∠3,
在△BEF和△CDH中,
,
∴△BEF≌△CDH(AAS).
19. (1)调查人数为:20÷0.1=200(名),
m=200×0.3=60(名),
n=10÷200=0.05,
故答案为:200,60,0.05;
(2)补全频数分布直方图如下:
(3)1200×=360(人),
答:全校安全意识不强的学生大约有360人.
20. (1)当0<x≤20时,设y=k1x,把(20,100)代入得k1=5,
∴y=5x;
当x≥20时,设y=,把(20,100)代入得k2=2000,
∴y=;
(2)当0<x≤20时,又5x≥80得,x≥16,即16≤x≤20,有5天;
当x>20时,由≥80,
解得:x≤25,即20<x≤25,有5天,
共有5+5=10(天),
因此设计师可以拿到“特殊贡献奖”.
21. (1)16y2﹣24y+9=0,
∵Δ=(﹣24)2﹣4×16×9=0,
∴方程有两个相等的实数根;
(2)5x2﹣7x+5=0
∵Δ=(﹣7)2﹣4×5×5=﹣51<0,
∴方程没有实数根;
(3)∵Δ=[﹣(m+3)]2﹣4m=(m+1)2+8>0,
∴方程有两个不相等的实数根.
22. (1)如图,过A点作AM⊥BC于M,交EF于N.
∵AB=AC=6,BC=4,
∴BM=MC=BC=2,
∴AM===4,
∴sinB===;
(2)∵点E、F分别是AB、AC的中点,
∴AE=AB=AC=AF=3,EF∥BC,EF=BC=2,
∵AM⊥BC,
∴AM⊥EF,即AN⊥EF,
∴EN=NF=EF=1,
∴AN2=AE2﹣EN2=32﹣12=8.
∵CD∥AB,EF∥BC,
∴四边形BCDE是平行四边形,
∴DE=BC=4,
∴DN=DE﹣EN=4﹣1=3,
∴AD===.
故线段AD的长为.
23. 如图,过点C作CD⊥AB交AB于点D.设CD=x,
∵无人机在空中C处测得地面A、B两点的俯角分别为30°、45°,
∴∠A=30°,∠B=45°,
在Rt△BCD中,∠B=∠BCD=45°,
∴BD=CD=x,
在Rt△ACD中,∵,
∴,
∴,
∵,
即,
解得x=15,
∴CD=15(米).
答:无人机距地面高度CD为15米.
24. (1)将A(﹣1,0),B(3,0),C(0,﹣2)代入y=ax2+bx+c(a≠0),
得:a﹣b+c=0,9a﹣3b+c=0,c=﹣2,
解得:,,c=﹣2,
∴;
(2)当时,,
∴,
∴,
当时,,
∴PD=2m﹣6,
∴P(m,2m﹣6),
综上,P(m,2m﹣6)或;
(3)如图,过点Q作QM⊥l于点M
∵△BPQ为等腰直角三角形,∠BPQ=90°,PQ=BP,
又∵∠QMP=∠BDP=90°,
∴△BDP≌△PMQ(AAS),
∴QM=PD,PM=BD,
①当P为时,,,
∴,
代入,
解得:m1=4,m2=3(舍去)
∴
②当P为(m,2m﹣6)时,QM=PD=2m﹣6,DM=PM+PD=3m﹣9,
∴Q(6﹣m,3m﹣9),
代入,
解得:,m2=3(舍去)
∴,
此时的点Q不在第一象限内,故舍去,
综上,可得.
25. (1)证明:方法1,平移线段FG至BH交AE于点K,如图1﹣1所示:
由平移的性质得:FG∥BH,
∵四边形ABCD是正方形,
∴AB∥CD,AB=BC,∠ABE=∠C=90°,
∴四边形BFGH是平行四边形,
∴BH=FG,
∵FG⊥AE,
∴BH⊥AE,
∴∠BKE=90°,
∴∠KBE+∠BEK=90°,
∵∠BEK+∠BAE=90°,
∴∠BAE=∠CBH,
在△ABE和△BCH中,
,
∴△ABE≌△BCH(ASA),
∴AE=BH,
∴AE=FG;
方法2:平移线段BC至FH交AE于点K,如图1﹣2所示:
则四边形BCHF是矩形,∠AKF=∠AEB,
∴FH=BC,∠FHG=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=90°,
∴AB=FH,∠ABE=∠FHG,
∵FG⊥AE,
∴∠HFG+∠AKF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠HFG,
在△ABE和△FHG中,
,
∴△ABE≌△FHG(ASA),
∴AE=FG;
(2)解:将线段AB向右平移至FD处,使得点B与点D重合,连接CF,如图2所示:
∴∠AOC=∠FDC,
设正方形网格的边长为单位1,
则AC=2,AF=1,CE=2,DE=4,FG=3,DG=4,
由勾股定理可得:CF===,CD===2,DF===5,
∵()2+(2)2=52,
∴CF2+CD2=DF2,
∴∠FCD=90°,
∴tan∠AOC=tan∠FDC===;
(3)解:①平移线段BC至DG处,连接GE,如图3﹣1所示:
则∠DMC=∠GDE,四边形DGBC是平行四边形,
∴DC=GB,
∵四边形ADCP与四边形PBEF都是正方形,
∴DC=AD=AP,BP=BE,∠DAG=∠GBE=90°
∴DC=AD=AP=GB,
∴AG=BP=BE,
在△AGD和△BEG中,
,
∴△AGD≌△BEG(SAS),
∴DG=EG,∠ADG=∠EGB,
∴∠EGB+∠AGD=∠ADG+∠AGD=90°,
∴∠EGD=90°,
∴∠GDE=∠GED=45°,
∴∠DMC=∠GDE=45°;
②如图3﹣2所示:
∵AC为正方形ADCP的对角线,
∴AD=CD,∠DAC=∠PAC=∠DMC=45°,
∴△ACD是等腰直角三角形,
∴AC=AD,
∵∠HCM=∠BCA,
∴∠AHD=∠CHM=∠ABC,
∴△ADH∽△ACB,
∴===.
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)如图是一个几何体水箱的表面展开图,根据图中标注的尺寸,则该几何体的表面积为( )
A.28π B.32π C.33π D.35π
2.(3分)下列图形中,是中心对称图形的是( )
A. B. C. D.
3.(3分)若代数式有意义,则实数x的取值范围是( )
A.x≥﹣2 B.x≥﹣2,且x≠0 C.x>﹣2 D.x≤﹣2,且x≠0
4.(3分)点(3,﹣5)在正比例函数y=kx(k≠0)的图象上,则k的值为( )
A.﹣15 B.15 C.﹣ D.﹣
5.(3分)下列运算正确的是( )
A.﹣= B.=﹣3 C.=2 D.=+
6.(3分)如图,正方形的周长为8个单位,在该正方形的4个顶点处分别标上0、2、4、6,先让正方形上表示数字6的点与数轴上表示﹣3的点重合,再将数轴按顺时针方向环绕在该正方形上.则数轴上表示99的点与正方形上表示数字( )的点重合.
A.0 B.2 C.4 D.6
7.(3分)某校开展“文明小卫士”活动,从学生会的2名男生和1名女生中随机选取两名进行督查,恰好选中两名男生的概率是( )
A. B. C. D.
8.(3分)二次函数y=4ax2+4bx+1与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.(3分)在一次数学课上,张老师出示了一个题目:“如图, ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )
A.小青 B.小何 C.小夏 D.小雨
10.(3分)下列图中所有小正方形都是全等的.图1是一张由4个小正方形组成的“凸”形纸片,图2是一张由6个小正方形组成的3×2方格纸片.把“凸”形纸片放置在图2中,使它恰好盖住其中的4个小正方形,共有如图3中的2种不同放置方法.图4是一张由36个小正方形组成的6×6方格纸片,将“凸”形纸片放置在图4中,使它恰好盖住其中的4个小正方形,共有n种不同放置方法,则n的值是( )
A.160 B.128 C.80 D.48
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)中华民族的文化博大精深、源远流长,中华汉字寓意深广.为弘扬中华优秀传统文化,太原市某校开展了一次书法大赛活动,经过6轮激烈的角逐,小明和小红两人进入决赛,两人的成绩如图所示,他们成绩的方差分别为s小明2与s小红2,则s小明2 s小红2.(填“>”、“=”或“<”)
12.(3分)因式分解:(m﹣1)2+2m﹣2= .
13.(3分)如图,在平行四边形ABCD中,已知AD=8cm,BE=2cm,DE平分∠ADC交BC边于点E,则AB= cm.
14.(3分)方程=2的解是x= .
15.(3分)如图,在直角坐标系中,四边形ABCD是正方形,A(1,﹣1),B(﹣1,﹣1),C(﹣1,1),D(1,1).曲线AA1A2A3…叫做“正方形的渐开线”,其中弧AA1、弧A1A2、弧A2A3、弧A3A4…所在圆的圆心依次是点B、C、D、A循环,则点A2015坐标是 .
16.(3分)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D',点A的对应点A'在对角线AC上,点C、D分别与点C'、D'对应,A′D'与边BC交于点E,那么BE的长是 .
三.解答题(共9小题,满分72分)
17.(4分)解下列不等式:
(1)5x﹣2>3(x﹣2).
(2)<1﹣.
18.(4分)如图,在△ABC中,AD平分∠BAC交BC于点D,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)试在图中找出一对全等的三角形,并给予证明.
19.(6分)某校为提高学生的安全意识,组织全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩(分数为正整数,满分100分)进行统计,并制作不完全统计图表:
分数段 频数 频率
50≤x<60 20 0.1
60≤x<70 40 0.2
70≤x<80 70 0.35
80≤x<90 m 0.3
90≤x<100 10 n
请根据所给数据解答下列问题:
(1)这次共抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(不含70分)视为安全意识不强,有待进一步加强安全教育,请估计全校安全意识不强的学生人数.
20.(6分)某种商品上市之初采用了大量的广告宣传,其日销售量y与上市的天数x之间成正比例函数,当广告停止后,日销售量y与上市的天数x之间成反比例函数(如图所示),现已知上市20天时,当日销售量为100件.
(1)写出该商品上市以后日销售量y件与上市的天数x天之间的表达式;
(2)广告合同约定,当日销售量不低于80件,并且持续天数不少于10天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”,并说明理由?
21.(8分)不解方程判别方程根的情况:
(1)16y2+9=24y;
(2)5(x2+1)﹣7x=0;
(3)x2﹣(m+3)x+m=0(m为常数).
22.(10分)如图,已知在△ABC中,AB=AC=6,BC=4,点E、F分别是AB、AC的中点,过点C作CD∥AB交EF的延长线于点D,联结AD.
(1)求∠B的正弦值;
(2)求线段AD的长.
23.(10分)如图,无人机在空中C处测得地面A、B两点的俯角分别为30°、45°,点A、B在同一水平地面上,如果测得A、B两点间的距离是15+15米.
求无人机与地面的垂直高度是多少米?
24.(12分)二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,﹣2),直线l:x=m(m>3)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线l上找点P(点P在第一象限),使得以点P,D,B为顶点的三角形与以点A,C,O为顶点的三角形相似,求点P的坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在第一象限内的点Q,使得△BPQ是以P为直角顶点的等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
25.(12分)【问题情境】
(1)如图1,在正方形ABCD中,E,F,G分别是BC,AB,CD上的点,FG⊥AE于点Q.求证:AE=FG.
【尝试应用】
(2)如图2,正方形网格中,点A,B,C,D为格点,AB交CD于点O.求tan∠AOC的值;
【拓展提升】
(3)如图3,点P是线段AB上的动点,分别以AP,BP为边在AB的同侧作正方形APCD与正方形PBEF,连接DE分别交线段BC,PC于点M,N.
①求∠DMC的度数;
②连接AC交DE于点H,直接写出的值.
参考答案
1.B
2.D
3.B
4.D
5.A
6.C
7.A
8.D
9.B
10.C
11. <.
12. (m﹣1)(m+1).
13. 6.
14. ﹣5.
15. (1,4031).
16. .
17. (1)5x﹣2>3(x﹣2),
去括号得,5x﹣2>3x﹣6,
移项得,5x﹣3x>﹣6+2,
合并同类项得,2x>﹣4,
系数化为1得,x>﹣2;
(2)<1﹣,
去分母得,2x<6﹣(x﹣3),
去括号得,2x<6﹣x+3,
移项得,2x+x<6+3,
合并同类项得,3x<9,
系数化为1得,x<3.
18. (1)证明:如图.
∵EF∥AD,
∴∠1=∠4,∠2=∠P,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠4=∠P,
∴AF=AP,
即△APF是等腰三角形;
(2)解:△BEF≌△CDH.理由如下:
∵CH∥AB,
∴∠5=∠B,∠H=∠1,
∵EF∥AD,
∴∠1=∠3,
∴∠H=∠3,
在△BEF和△CDH中,
,
∴△BEF≌△CDH(AAS).
19. (1)调查人数为:20÷0.1=200(名),
m=200×0.3=60(名),
n=10÷200=0.05,
故答案为:200,60,0.05;
(2)补全频数分布直方图如下:
(3)1200×=360(人),
答:全校安全意识不强的学生大约有360人.
20. (1)当0<x≤20时,设y=k1x,把(20,100)代入得k1=5,
∴y=5x;
当x≥20时,设y=,把(20,100)代入得k2=2000,
∴y=;
(2)当0<x≤20时,又5x≥80得,x≥16,即16≤x≤20,有5天;
当x>20时,由≥80,
解得:x≤25,即20<x≤25,有5天,
共有5+5=10(天),
因此设计师可以拿到“特殊贡献奖”.
21. (1)16y2﹣24y+9=0,
∵Δ=(﹣24)2﹣4×16×9=0,
∴方程有两个相等的实数根;
(2)5x2﹣7x+5=0
∵Δ=(﹣7)2﹣4×5×5=﹣51<0,
∴方程没有实数根;
(3)∵Δ=[﹣(m+3)]2﹣4m=(m+1)2+8>0,
∴方程有两个不相等的实数根.
22. (1)如图,过A点作AM⊥BC于M,交EF于N.
∵AB=AC=6,BC=4,
∴BM=MC=BC=2,
∴AM===4,
∴sinB===;
(2)∵点E、F分别是AB、AC的中点,
∴AE=AB=AC=AF=3,EF∥BC,EF=BC=2,
∵AM⊥BC,
∴AM⊥EF,即AN⊥EF,
∴EN=NF=EF=1,
∴AN2=AE2﹣EN2=32﹣12=8.
∵CD∥AB,EF∥BC,
∴四边形BCDE是平行四边形,
∴DE=BC=4,
∴DN=DE﹣EN=4﹣1=3,
∴AD===.
故线段AD的长为.
23. 如图,过点C作CD⊥AB交AB于点D.设CD=x,
∵无人机在空中C处测得地面A、B两点的俯角分别为30°、45°,
∴∠A=30°,∠B=45°,
在Rt△BCD中,∠B=∠BCD=45°,
∴BD=CD=x,
在Rt△ACD中,∵,
∴,
∴,
∵,
即,
解得x=15,
∴CD=15(米).
答:无人机距地面高度CD为15米.
24. (1)将A(﹣1,0),B(3,0),C(0,﹣2)代入y=ax2+bx+c(a≠0),
得:a﹣b+c=0,9a﹣3b+c=0,c=﹣2,
解得:,,c=﹣2,
∴;
(2)当时,,
∴,
∴,
当时,,
∴PD=2m﹣6,
∴P(m,2m﹣6),
综上,P(m,2m﹣6)或;
(3)如图,过点Q作QM⊥l于点M
∵△BPQ为等腰直角三角形,∠BPQ=90°,PQ=BP,
又∵∠QMP=∠BDP=90°,
∴△BDP≌△PMQ(AAS),
∴QM=PD,PM=BD,
①当P为时,,,
∴,
代入,
解得:m1=4,m2=3(舍去)
∴
②当P为(m,2m﹣6)时,QM=PD=2m﹣6,DM=PM+PD=3m﹣9,
∴Q(6﹣m,3m﹣9),
代入,
解得:,m2=3(舍去)
∴,
此时的点Q不在第一象限内,故舍去,
综上,可得.
25. (1)证明:方法1,平移线段FG至BH交AE于点K,如图1﹣1所示:
由平移的性质得:FG∥BH,
∵四边形ABCD是正方形,
∴AB∥CD,AB=BC,∠ABE=∠C=90°,
∴四边形BFGH是平行四边形,
∴BH=FG,
∵FG⊥AE,
∴BH⊥AE,
∴∠BKE=90°,
∴∠KBE+∠BEK=90°,
∵∠BEK+∠BAE=90°,
∴∠BAE=∠CBH,
在△ABE和△BCH中,
,
∴△ABE≌△BCH(ASA),
∴AE=BH,
∴AE=FG;
方法2:平移线段BC至FH交AE于点K,如图1﹣2所示:
则四边形BCHF是矩形,∠AKF=∠AEB,
∴FH=BC,∠FHG=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=90°,
∴AB=FH,∠ABE=∠FHG,
∵FG⊥AE,
∴∠HFG+∠AKF=90°,
∵∠AEB+∠BAE=90°,
∴∠BAE=∠HFG,
在△ABE和△FHG中,
,
∴△ABE≌△FHG(ASA),
∴AE=FG;
(2)解:将线段AB向右平移至FD处,使得点B与点D重合,连接CF,如图2所示:
∴∠AOC=∠FDC,
设正方形网格的边长为单位1,
则AC=2,AF=1,CE=2,DE=4,FG=3,DG=4,
由勾股定理可得:CF===,CD===2,DF===5,
∵()2+(2)2=52,
∴CF2+CD2=DF2,
∴∠FCD=90°,
∴tan∠AOC=tan∠FDC===;
(3)解:①平移线段BC至DG处,连接GE,如图3﹣1所示:
则∠DMC=∠GDE,四边形DGBC是平行四边形,
∴DC=GB,
∵四边形ADCP与四边形PBEF都是正方形,
∴DC=AD=AP,BP=BE,∠DAG=∠GBE=90°
∴DC=AD=AP=GB,
∴AG=BP=BE,
在△AGD和△BEG中,
,
∴△AGD≌△BEG(SAS),
∴DG=EG,∠ADG=∠EGB,
∴∠EGB+∠AGD=∠ADG+∠AGD=90°,
∴∠EGD=90°,
∴∠GDE=∠GED=45°,
∴∠DMC=∠GDE=45°;
②如图3﹣2所示:
∵AC为正方形ADCP的对角线,
∴AD=CD,∠DAC=∠PAC=∠DMC=45°,
∴△ACD是等腰直角三角形,
∴AC=AD,
∵∠HCM=∠BCA,
∴∠AHD=∠CHM=∠ABC,
∴△ADH∽△ACB,
∴===.
同课章节目录
