【备考2023】浙教版科学“冲刺重高”压轴训练(二十八):物理仪器原理探究(含解析)
文档属性
| 名称 | 【备考2023】浙教版科学“冲刺重高”压轴训练(二十八):物理仪器原理探究(含解析) | 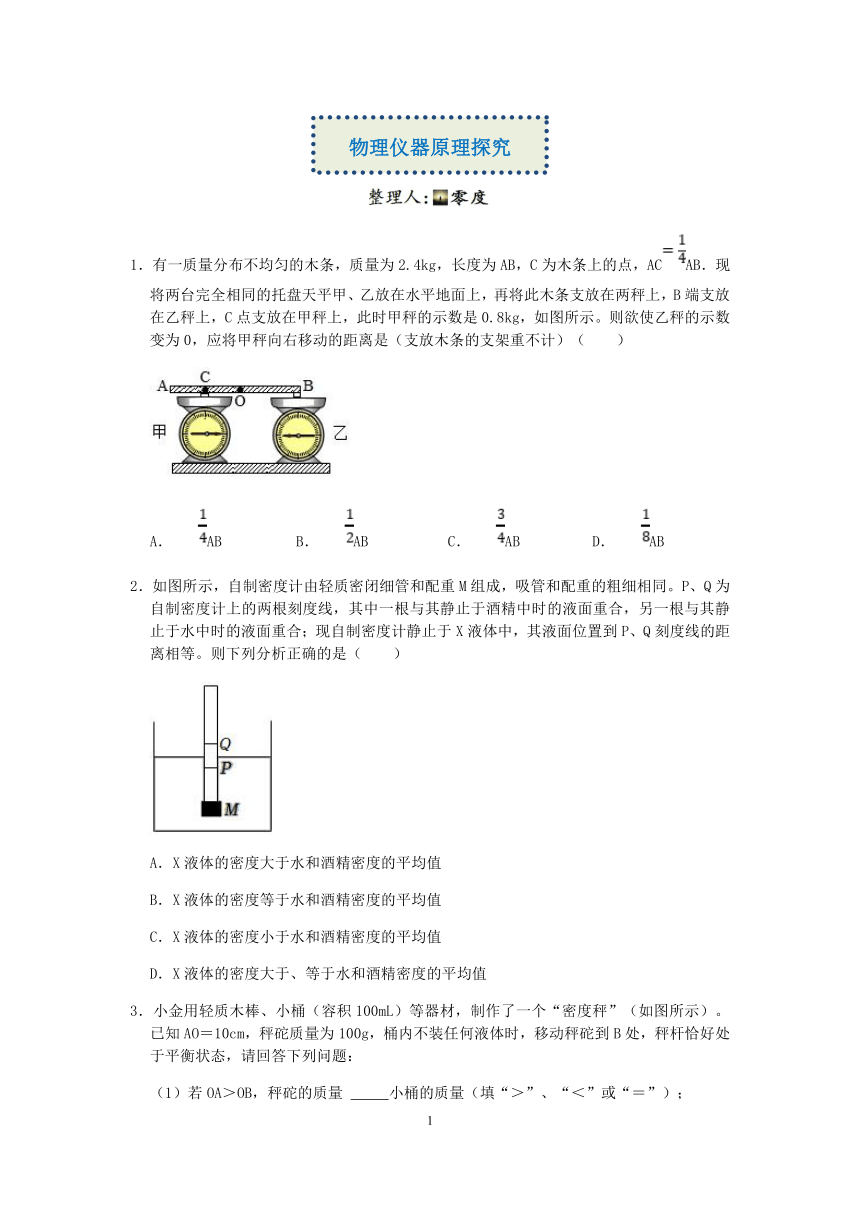 | |
| 格式 | doc | ||
| 文件大小 | 548.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-05-18 20:57:15 | ||
图片预览



文档简介
1.有一质量分布不均匀的木条,质量为2.4kg,长度为AB,C为木条上的点,ACAB.现将两台完全相同的托盘天平甲、乙放在水平地面上,再将此木条支放在两秤上,B端支放在乙秤上,C点支放在甲秤上,此时甲秤的示数是0.8kg,如图所示。则欲使乙秤的示数变为0,应将甲秤向右移动的距离是(支放木条的支架重不计)( )
A.AB B.AB C.AB D.AB
2.如图所示,自制密度计由轻质密闭细管和配重M组成,吸管和配重的粗细相同。P、Q为自制密度计上的两根刻度线,其中一根与其静止于酒精中时的液面重合,另一根与其静止于水中时的液面重合;现自制密度计静止于X液体中,其液面位置到P、Q刻度线的距离相等。则下列分析正确的是( )
A.X液体的密度大于水和酒精密度的平均值
B.X液体的密度等于水和酒精密度的平均值
C.X液体的密度小于水和酒精密度的平均值
D.X液体的密度大于、等于水和酒精密度的平均值
3.小金用轻质木棒、小桶(容积100mL)等器材,制作了一个“密度秤”(如图所示)。已知AO=10cm,秤砣质量为100g,桶内不装任何液体时,移动秤砣到B处,秤杆恰好处于平衡状态,请回答下列问题:
(1)若OA>OB,秤砣的质量 小桶的质量(填“>”、“<”或“=”);
(2)该秤的刻度是 (选填“均匀”或“不均匀”)的;
(3)当小金向桶内装满某种液体后,需将秤砣向右移动8cm,秤杆再次达到平衡状态,则该液体的密度为 kg/m3。
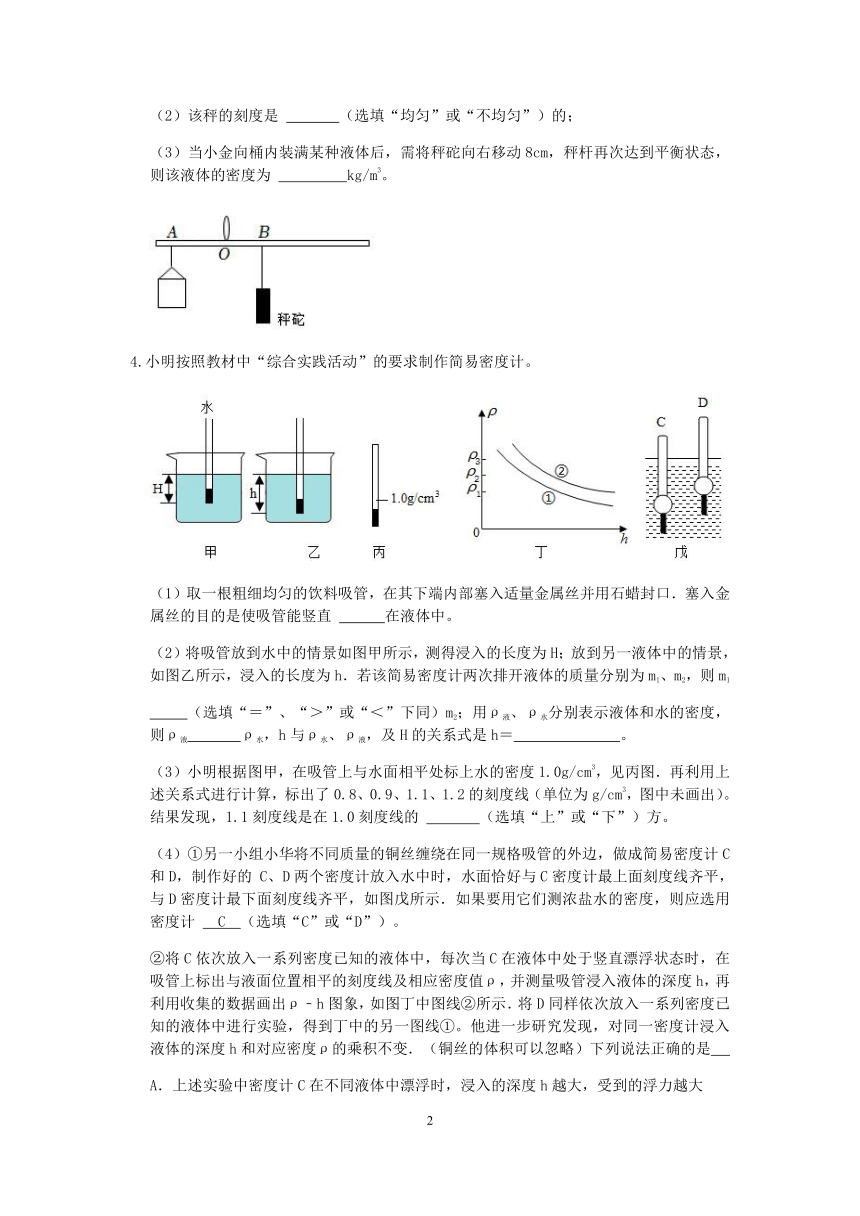
4.小明按照教材中“综合实践活动”的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端内部塞入适量金属丝并用石蜡封口.塞入金属丝的目的是使吸管能竖直 在液体中。
(2)将吸管放到水中的情景如图甲所示,测得浸入的长度为H;放到另一液体中的情景,如图乙所示,浸入的长度为h.若该简易密度计两次排开液体的质量分别为m1、m2,则m1
(选填“=”、“>”或“<”下同)m2;用ρ液、ρ水分别表示液体和水的密度,则ρ液 ρ水,h与ρ水、ρ液,及H的关系式是h= 。
(3)小明根据图甲,在吸管上与水面相平处标上水的密度1.0g/cm3,见丙图.再利用上述关系式进行计算,标出了0.8、0.9、1.1、1.2的刻度线(单位为g/cm3,图中未画出)。结果发现,1.1刻度线是在1.0刻度线的 (选填“上”或“下”)方。
(4)①另一小组小华将不同质量的铜丝缠绕在同一规格吸管的外边,做成简易密度计C和D,制作好的 C、D两个密度计放入水中时,水面恰好与C密度计最上面刻度线齐平,与D密度计最下面刻度线齐平,如图戊所示.如果要用它们测浓盐水的密度,则应选用密度计 C (选填“C”或“D”)。
②将C依次放入一系列密度已知的液体中,每次当C在液体中处于竖直漂浮状态时,在吸管上标出与液面位置相平的刻度线及相应密度值ρ,并测量吸管浸入液体的深度h,再利用收集的数据画出ρ﹣h图象,如图丁中图线②所示.将D同样依次放入一系列密度已知的液体中进行实验,得到丁中的另一图线①。他进一步研究发现,对同一密度计浸入液体的深度h和对应密度ρ的乘积不变.(铜丝的体积可以忽略)下列说法正确的是
A.上述实验中密度计C在不同液体中漂浮时,浸入的深度h越大,受到的浮力越大
B.密度计C上缠绕铜丝的质量小于密度计D上缠绕铜丝的质量
C.若图丁中ρ3﹣ρ2=ρ2﹣ρ1,则密度计C上ρ3与ρ2刻度线的间距大于ρ2与ρ1刻度线的间距
D.若图丁中ρ3﹣ρ2=ρ2﹣ρ1,则密度计C上ρ3与ρ1刻度线的间距大于密度计D上ρ3与ρ1刻度线的间距
5.小明同学听了“曹冲称象”的故事后,利用所学知识制作了如图甲所示的“水秤”模型,可方便地称量物体的质量,其构造如图所示,已知透明大桶足够深,小筒的高度为H=0.2m,底面积为S=0.02m ,小筒和秤盘总重量为1N,小筒壁的厚度可忽略不计。g=10N/kg,ρ水=1.0×103kg/m3。求:
(1)如图甲所示,当秤盘上不放物体时,小筒处于 (选填“漂浮”或“悬浮”)状态,此时小筒受到的浮力是多少?
(2)该浮力秤的零刻度线应标在小筒上何处(即A点距小筒底部的距离)?
(3)如图乙所示,在秤盘上放物体后,就可以称量物体所受重力。则该“水秤”模型最大能称量的物体重量为多大?
6.小金想制作一台浮力秤,他将一段密度为0.5×103kg/m3均匀的长方体木料,先进行不吸水处理,再将其放于水中。如图所示,这段木料始终竖立,高度为40cm,底部横截面积为0.1m2,其上表面可以作为秤盘。问:
(a)木料的质量是多少千克?
(b)当木料上不放置任何物体时,木料底部浸入水中的深度为多少米?
(c)当木料上放置一物体时,木料露出水面高度为10cm,求对应称量物体的质量为多少千克?
7.下面是小刚自制“浮力秤”的装置图(如图甲)和使用说明书(如图乙)。
已知“浮力秤”内所装的液体是水,秤盘中未放物体时浮体的圆柱体浸入水中的深度h0为4cm,请根据上述内容和条件解答:
请你完成下列问题:
(1)“浮力秤”能够称出物体的质量,应用原理是始终让浮力秤的浮体处于 (选填“上浮”、“漂浮”或“悬浮”)状态。
(2)根据小刚制作出的“浮力秤”参数可得,秤盘没有放物体时浮体排开水的体积是
cm3,这“浮力秤”的浮体质量是 kg;根据“浮力秤”的使用说明书可知,应把“浮力秤”的刻度刻在 (选填“浮体”或“外筒”)壁上,且刻度是 (选填“均匀”或“不均匀”)的;
(3)理想状态下,使用此“浮力秤”能够达到最大称量值是 kg;达到最大称量时,应在外筒中至少加入 kg的水。
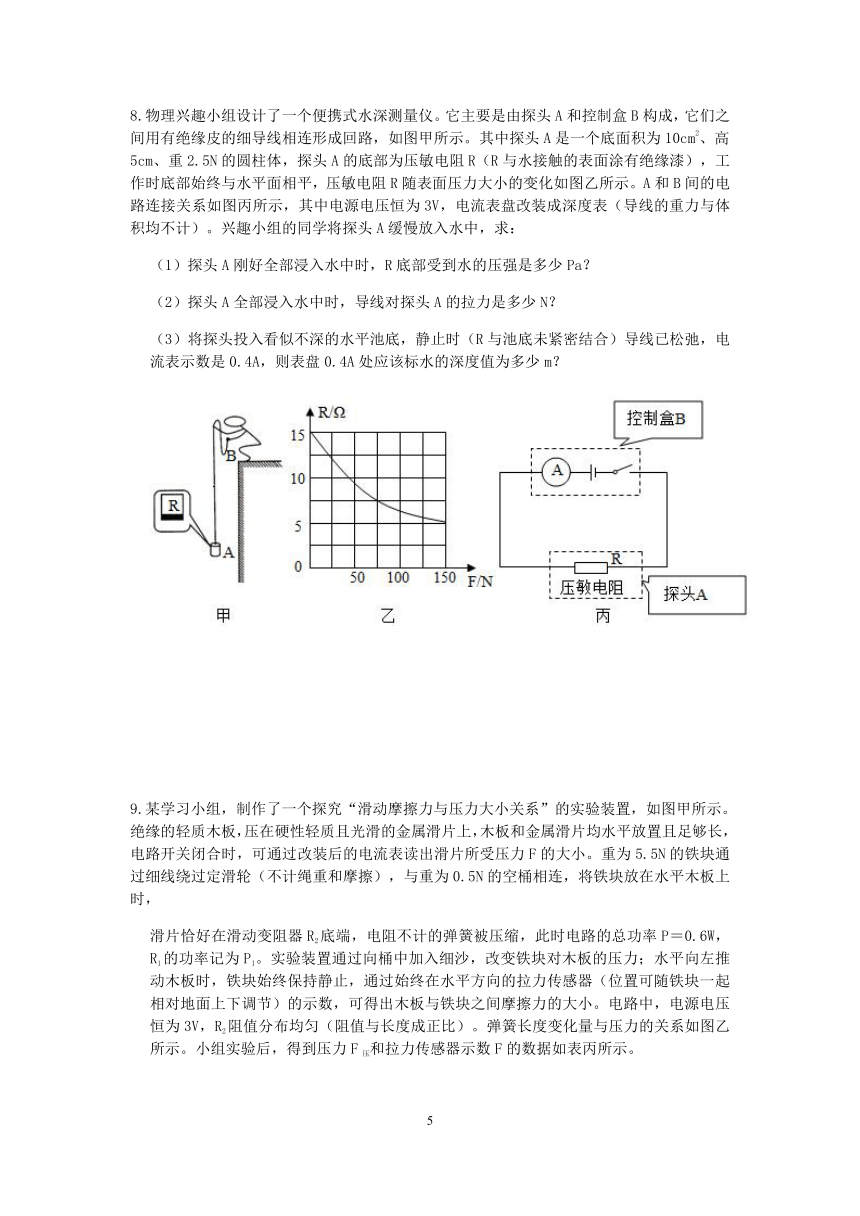
8.物理兴趣小组设计了一个便携式水深测量仪。它主要是由探头A和控制盒B构成,它们之间用有绝缘皮的细导线相连形成回路,如图甲所示。其中探头A是一个底面积为10cm2、高5cm、重2.5N的圆柱体,探头A的底部为压敏电阻R(R与水接触的表面涂有绝缘漆),工作时底部始终与水平面相平,压敏电阻R随表面压力大小的变化如图乙所示。A和B间的电路连接关系如图丙所示,其中电源电压恒为3V,电流表盘改装成深度表(导线的重力与体积均不计)。兴趣小组的同学将探头A缓慢放入水中,求:
(1)探头A刚好全部浸入水中时,R底部受到水的压强是多少Pa?
(2)探头A全部浸入水中时,导线对探头A的拉力是多少N?
(3)将探头投入看似不深的水平池底,静止时(R与池底未紧密结合)导线已松弛,电流表示数是0.4A,则表盘0.4A处应该标水的深度值为多少m?
9.某学习小组,制作了一个探究“滑动摩擦力与压力大小关系”的实验装置,如图甲所示。绝缘的轻质木板,压在硬性轻质且光滑的金属滑片上,木板和金属滑片均水平放置且足够长,电路开关闭合时,可通过改装后的电流表读出滑片所受压力F的大小。重为5.5N的铁块通过细线绕过定滑轮(不计绳重和摩擦),与重为0.5N的空桶相连,将铁块放在水平木板上时,
滑片恰好在滑动变阻器R2底端,电阻不计的弹簧被压缩,此时电路的总功率P=0.6W,R1的功率记为P1。实验装置通过向桶中加入细沙,改变铁块对木板的压力;水平向左推动木板时,铁块始终保持静止,通过始终在水平方向的拉力传感器(位置可随铁块一起相对地面上下调节)的示数,可得出木板与铁块之间摩擦力的大小。电路中,电源电压恒为3V,R2阻值分布均匀(阻值与长度成正比)。弹簧长度变化量与压力的关系如图乙所示。小组实验后,得到压力F压和拉力传感器示数F的数据如表丙所示。
F压/N 0 1 2 3 4 5
F/N 0 0.25 0.5 0.75 1 1.25
(1)若铁块的底面积为20cm2,当F=1N时,铁块对木板的压强为多少?
(2)学习小组应当将电流表的哪个刻度改为压力5N?
(3)若压力为0时,滑片恰好在R2的顶端,此时R1的功率记为P2,且P1:P2=1:9当电流表的示数为0.5A时,向桶中加入细沙的重力为多少?
参考答案
1.解:木条的重力:G=mg=2.4kg×10N/kg=24N;
设木条重心在D点,当C点放在托盘秤甲上,B端放在托盘秤乙上时,以B端为支点,
托盘秤甲的示数是0.8kg,则托盘受到的压力:F压=mCg=0.8kg×10N/kg=8N,
根据力的作用是相互的,所以托盘秤对木条C点的支持力为8N,如图所示:
由杠杆平衡条件有:FC×CB=G×BD,即:8N×CB=24N×BD,
所以:CB=3BD,
因ACAB,所以CBAB
则BDABAB,
CD=AB﹣AC﹣BD=ABABABAB,
欲使乙秤的示数变为0,需将甲秤移到D点,故向右移动的距离为AB。
故选:B。
2.解:因为密度计在使用时始终处于漂浮状态,浮力大小等于重力大小,密度计的重力不变,浮力不变,由阿基米德原理可知,液体密度与密度计浸入液体深度的关系为:ρ液,则液体的密度越大密度计浸入液体深度小,又水的密度大于酒精的密度,所以P与自制密度计静止于水中时的液面重合,Q与自制密度计静止于酒精中时的液面重合;
由ρ液可知,所测液体的密度与密度计浸入液体的深度成反比,液体密度越大,浸入深度越小,所以密度计下端刻度大,并且刻度是不均匀的,上疏下密。当X液体液面位置在PQ中点时,此X液体的密度在水和酒精密度的中点,故此液体密度小于水和酒精密度的平均值,故C正确。
故选:C。
3.解:(1)由杠杆的平衡条件F1l1=F2l2可得m桶g×OA=m秤砣g×OB,即m桶×OA=m秤砣×OB,由于OA>OB,所以m桶<m秤砣;
(2)设桶内装满密度为ρ液的某种液体后,秤砣由B点向右移动到C点,秤杆再次达到平衡状态后,
由杠杆的平衡条件F1l1=F2l2可得:(m桶+m液)g×OA=m秤砣g×(OB+BC),
又m桶g×OA=m秤砣g×OB,
化简得:m液×OA=m秤砣×BC,
又m液=ρ液V液,代入可得:ρ液,由于OA、m秤砣、V液是定值,所以ρ液与BC成正比,即该秤的刻度是均匀的;
(3)把OA=10cm,BC=8cm,m秤砣=100g,V液=100mL=100cm3代入ρ液中可得:ρ液0.8g/cm3=0.8×103kg/m3。
故答案为:(1)>;(2)均匀;(3)0.8×103。
4.解:
(1)取一根粗细均匀的饮料吸管,在其下端内部塞入适量金属丝并用石蜡封口,这样做目的是为了降低重心,让吸管竖直漂浮在液体中;
(2)由于吸管在(a)、(b)图中均漂浮,所以F浮=G,
则在水和另一种液体中受到的浮力相等,F浮水=F浮夜,根据公式F浮=G排=m排g=ρ液gV排得:m1=m2;
由图可知,V排液>V排水,则ρ液<ρ水,
设吸管的底面积为S,根据阿基米德原理F浮=G排=m排g=ρgV排得,ρ水gSH=ρ液gSh,
解得:h;
(3)根据(2)可知,ρ液和h是反比例函数,将上端刻度与下端刻度进行比较,得到刻度线的两个特点是:上端刻度小、下端刻度大,即1.1刻线是在1.0刻线的下方;
(4)①密度计漂浮在液面上时,所受浮力等于其重力;水的密度小于浓盐水的密度,所以在浓盐水中漂浮时,由V排知,密度计排开浓盐水的体积小于排开水的体积,也就是密度计从水中取出放入浓盐水后,会上浮一些。因此只能选择C密度计。
②A、由于密度计C在不同液体中静止时都处于漂浮状态,则F浮=G,即密度计C在不同液体中受到的浮力相等,都等于密度计C受到的重力G,故A错误;
B、密度计C与D是由不同质量的铜丝缠绕在同一规格吸管的外边制成的,由图知,密度计浸入液体的深度相同时,即密度计排开液体的体积相同,由图知,C测量的液体的密度大,根据F浮=ρ液gV排可知:密度计C受到的浮力大,根据漂浮条件可知:密度计C的重力大于D的重力,所以,密度计C上缠绕铜丝的重力大于密度计D上缠绕铜丝的重力,则密度计C上缠绕铜丝的质量大于密度计D上缠绕铜丝的质量,故B错误;
C、密度计C分别测量液体ρ1、ρ2、ρ3时,根据漂浮条件和F浮=ρ液gV排可知密度计C浸入液体的深度分别为:h1,h2;
则密度计C上ρ2与ρ1刻度线的间距:△h21=h1﹣h2;
密度计C上ρ3与ρ2刻度线的间距:△h32=h2﹣h3;
由图知:ρ1<ρ2<ρ3,若ρ3﹣ρ2=ρ2﹣ρ1,则:Δh32:Δh21=( ):( )=ρ1:ρ3<1,所以,△h32<△h21,即:密度计C上ρ3与ρ2刻度线的间距小于ρ2与ρ1刻度线的间距,故C错误。
D、密度计C上ρ3与ρ1刻度线的间距:△h31=h1﹣h3;
同理可得、密度计D分别测量液体ρ1、ρ2、ρ3时,根据漂浮条件和F浮=ρ液gV排可知密度计D浸入液体的深度分别为:
h1′,h2′,h3′;
密度计D上ρ3与ρ1刻度线的间距:△h31′=h1′﹣h3′;
则:Δh31:Δh31′=( ):( )=GC:GD>1,即密度计C上ρ3与ρ1刻度线的间距大于密度计D上ρ3与ρ1刻度线的间距,故D正确。
故选:D。
故答案为:(1)漂浮;(2)=;<; ;(3)下;(4)①C;②D。
5.解:(1)因为当秤盘上不放物体时,小筒漂浮,小筒和秤盘总重G0=1N,
所以此时小筒受到的浮力为:F浮=G0=1N;
(2)根据F浮=ρ液gV排得当秤盘上不放物体时,小筒排开水的体积为:
V排1×10﹣4m3,
由V=Sh得A点距小筒底部的距离:
h5×10﹣3m;
(3)在秤盘上放物体后小筒受到最大浮力为:
F浮′=ρ液gV排′=1.0×103kg/m3×10N/kg×0.02m2×0.2m=40N,
物体的最大重力为:
G=F浮′﹣G0=40N﹣1N=39N,
答:(1)漂浮;此时小筒受到的浮力是1N;
(2)该“浮力秤”的零刻度线应标在小筒上距小筒底部5×10﹣3m处;
(3)该“水秤”模型最大能称量的物体重量为39N。
6.解:(a)木料的体积:
V=Sh=0.1m2×0.4m=0.04m3,
由ρ可得,木料的质量:
m=ρV=0.5×103kg/m3×0.04m3=20kg,
(b)木料的重力:
G=mg=20kg×10N/kg=200N,
因木料静止时处于漂浮状态,受到的浮力和自身的重力相等,
由F浮=ρgV排可得,木料排开水的体积:
V排0.02m3,
木料浸入深度:
h0.2m;
(c)当木料上放置某物体时,木料排开水的体积:
V排′=S(h﹣h′)=0.1m2×(0.4m﹣0.1m)=0.03m3,
木料和物体受到的浮力:
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×0.03m3=300N,
因木料和物体整体处于漂浮状态,
所以,木料和物体的总重力G总=F浮′=300N,
则物体的重力:
G′=F浮′﹣G=300N﹣200N=100N,
对应称量物体的质量:
m′10kg。
答:(a)木料的质量是20kg;
(b)当木料上不放置任何物体时,木料浸入深度为0.2m;
(c)当木料上放置某物体时,对应称量物体的质量为10kg。
7.解:(1)“浮力秤”能够称出物体的质量,应用原理是漂浮的物体,所受的浮力等于自身的重力;
(2)秤盘没有放物体时浮体排开水的体积是:V排=Sh=250cm2×4cm=1000cm3;
浮体的浮力和重力分别用F浮1和G0表示,
浮体漂浮可得浮体重力:G0=F浮1=ρ水gV排1=1.0×103kg/m3×10N/kg×1000×10﹣6m3=10N,
浮体的质量:m01kg;
由说明可知,浮力秤是根据浮体在水中浸入的深度读数的,所以刻度线应刻在浮体上;
秤盘中未放物体时,浮体在水中漂浮,则有
F浮1=G0
ρ水gV排1=G0
化简后可得:G0=Sρ水gh0;=
被秤物体放在秤盘上后,浮体仍漂浮,则有
F浮2=G0+G物
ρ水gV排2=G0+mg
ρ水gSh=ρ水gSρh0+mg
化简后可得:m=Sρ水(h﹣h0);此式中,S、ρ水、h0均为定值,由此可知,m与h为一次函数,所以刻度是均匀的。
(3)由图可知,浮体的最大长度为40cm,能称得的最大质量:
m大=Sρ水(h﹣h0)=250×10﹣4m2×1.0×103kg/m3×(40﹣4)×10﹣2m=9kg;
达到最大称量时,应在外筒中加入水的体积:
V水=V容﹣V浮体=300×40×10﹣6m3﹣250×40×10﹣6m3=2×10﹣3m3,
水的质量:m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg。
故答案为:(1)漂浮;(2)1000;1;浮体;均匀;(3)9;2。
8.解:(1)探头A刚好全部浸入水中时,R底部的深度:h=5cm=0.05m,
R底部受到水的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(2)探头A全部浸入水中时,排开水的体积:V排=V=Sh=10cm2×5cm=50cm3=5×10﹣5m3,
受到的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×5×10﹣5m3=0.5N,
探头A处于平衡状态,由F浮=G﹣F′可得,导线对探头A的拉力:
F′=G﹣F浮=2.5N﹣0.5N=2N;
(3)由图丙可知,电路为压敏电阻R的简单电路,电流表测电路中的电流,
当电流表示数是0.4A时,由I可得,R的阻值:
R7.5Ω,
由图乙可知,压敏电阻R表面受到的压力F=75N,
探头A受到池底的支持力:
F支持=G﹣F浮=2.5N﹣0.5N=2N,
水对A底部的压力:
F水压=F﹣F支持=75N﹣2N=73N,
则压敏电阻受到水的压强:
p′7.3×104Pa,
水的深度:
h′7.3m,
所以,表盘0.4A处应该标水的深度值为7.3m。
答:(1)探头A刚好全部浸入水中时,R底部受到水的压强是500Pa;
(2)探头A全部浸入水中时,导线对探头A的拉力是2N;
(3)表盘0.4A处应该标水的深度值为7.3m。
9.解:(1)由表格可知当F=1N时,木板受到的压力F压=4N,铁块对木板的压强:p2000Pa;
(2)重为5.5N的铁块通过细线绕过定滑轮(不计绳重和摩擦),与重为0.5N的空桶相连,将铁块放在水平木板上时,滑片恰好在滑动变阻器R2底端,
此时铁块受到的压力:F压1=G铁块﹣G桶=5.5N﹣0.5N=5N,
此时定值电阻和滑动变阻器的最大电阻串联接入电路,电路的总功率P=0.6W,
通过电路的电流:I0.2A,
所以应当将电流表0.2A的刻度改为压力5N;
(3)定值电阻和滑动变阻器的最大电阻串联接入电路时,R1的功率记为P1,则P1=I2R1=(0.2A)2×R1,
压力为0时,滑片恰好在R2的顶端,此时电路为定值电阻的简单电路,此时R1的功率记为P2,则P2,
已知P1:P2=1:9,即,解方程可得R1=5Ω,
当电流表的示数为0.5A时,根据欧姆定律可得此时电路总电阻:R′6Ω,
串联电路总电阻等于各部分电阻之和,则滑动变阻器接入电路的阻值:R2=R′﹣R1=6Ω﹣5Ω=1Ω,
定值电阻和滑动变阻器的最大电阻串联接入电路时,电路总电阻:R15Ω,
滑动变阻器的最大阻值:R2=R﹣R1=15Ω﹣5Ω=10Ω,
由图乙可知弹簧的最大伸长量为5cm,弹簧受到的最大压力为5N,所以滑动变阻器的长度为5cm,
当电流表的示数为0.5A时,铁块受到的压力F压′5cm4.5N,
空桶和沙子的总重力:G=G铁块﹣F压′=5.5N﹣4.5N=1N,
向桶中加入细沙的重力为:G沙子=G﹣G桶=1N﹣0.5N=0.5N。
答:(1)若铁块的底面积为20cm2,当F=1N时,铁块对木板的压强为2000Pa;
(2)学习小组应当将电流表0.2A的刻度改为压力5N;
(3)当电流表的示数为0.5A时,向桶中加入细沙的重力为0.5N。
物理仪器原理探究
A.AB B.AB C.AB D.AB
2.如图所示,自制密度计由轻质密闭细管和配重M组成,吸管和配重的粗细相同。P、Q为自制密度计上的两根刻度线,其中一根与其静止于酒精中时的液面重合,另一根与其静止于水中时的液面重合;现自制密度计静止于X液体中,其液面位置到P、Q刻度线的距离相等。则下列分析正确的是( )
A.X液体的密度大于水和酒精密度的平均值
B.X液体的密度等于水和酒精密度的平均值
C.X液体的密度小于水和酒精密度的平均值
D.X液体的密度大于、等于水和酒精密度的平均值
3.小金用轻质木棒、小桶(容积100mL)等器材,制作了一个“密度秤”(如图所示)。已知AO=10cm,秤砣质量为100g,桶内不装任何液体时,移动秤砣到B处,秤杆恰好处于平衡状态,请回答下列问题:
(1)若OA>OB,秤砣的质量 小桶的质量(填“>”、“<”或“=”);
(2)该秤的刻度是 (选填“均匀”或“不均匀”)的;
(3)当小金向桶内装满某种液体后,需将秤砣向右移动8cm,秤杆再次达到平衡状态,则该液体的密度为 kg/m3。
4.小明按照教材中“综合实践活动”的要求制作简易密度计。
(1)取一根粗细均匀的饮料吸管,在其下端内部塞入适量金属丝并用石蜡封口.塞入金属丝的目的是使吸管能竖直 在液体中。
(2)将吸管放到水中的情景如图甲所示,测得浸入的长度为H;放到另一液体中的情景,如图乙所示,浸入的长度为h.若该简易密度计两次排开液体的质量分别为m1、m2,则m1
(选填“=”、“>”或“<”下同)m2;用ρ液、ρ水分别表示液体和水的密度,则ρ液 ρ水,h与ρ水、ρ液,及H的关系式是h= 。
(3)小明根据图甲,在吸管上与水面相平处标上水的密度1.0g/cm3,见丙图.再利用上述关系式进行计算,标出了0.8、0.9、1.1、1.2的刻度线(单位为g/cm3,图中未画出)。结果发现,1.1刻度线是在1.0刻度线的 (选填“上”或“下”)方。
(4)①另一小组小华将不同质量的铜丝缠绕在同一规格吸管的外边,做成简易密度计C和D,制作好的 C、D两个密度计放入水中时,水面恰好与C密度计最上面刻度线齐平,与D密度计最下面刻度线齐平,如图戊所示.如果要用它们测浓盐水的密度,则应选用密度计 C (选填“C”或“D”)。
②将C依次放入一系列密度已知的液体中,每次当C在液体中处于竖直漂浮状态时,在吸管上标出与液面位置相平的刻度线及相应密度值ρ,并测量吸管浸入液体的深度h,再利用收集的数据画出ρ﹣h图象,如图丁中图线②所示.将D同样依次放入一系列密度已知的液体中进行实验,得到丁中的另一图线①。他进一步研究发现,对同一密度计浸入液体的深度h和对应密度ρ的乘积不变.(铜丝的体积可以忽略)下列说法正确的是
A.上述实验中密度计C在不同液体中漂浮时,浸入的深度h越大,受到的浮力越大
B.密度计C上缠绕铜丝的质量小于密度计D上缠绕铜丝的质量
C.若图丁中ρ3﹣ρ2=ρ2﹣ρ1,则密度计C上ρ3与ρ2刻度线的间距大于ρ2与ρ1刻度线的间距
D.若图丁中ρ3﹣ρ2=ρ2﹣ρ1,则密度计C上ρ3与ρ1刻度线的间距大于密度计D上ρ3与ρ1刻度线的间距
5.小明同学听了“曹冲称象”的故事后,利用所学知识制作了如图甲所示的“水秤”模型,可方便地称量物体的质量,其构造如图所示,已知透明大桶足够深,小筒的高度为H=0.2m,底面积为S=0.02m ,小筒和秤盘总重量为1N,小筒壁的厚度可忽略不计。g=10N/kg,ρ水=1.0×103kg/m3。求:
(1)如图甲所示,当秤盘上不放物体时,小筒处于 (选填“漂浮”或“悬浮”)状态,此时小筒受到的浮力是多少?
(2)该浮力秤的零刻度线应标在小筒上何处(即A点距小筒底部的距离)?
(3)如图乙所示,在秤盘上放物体后,就可以称量物体所受重力。则该“水秤”模型最大能称量的物体重量为多大?
6.小金想制作一台浮力秤,他将一段密度为0.5×103kg/m3均匀的长方体木料,先进行不吸水处理,再将其放于水中。如图所示,这段木料始终竖立,高度为40cm,底部横截面积为0.1m2,其上表面可以作为秤盘。问:
(a)木料的质量是多少千克?
(b)当木料上不放置任何物体时,木料底部浸入水中的深度为多少米?
(c)当木料上放置一物体时,木料露出水面高度为10cm,求对应称量物体的质量为多少千克?
7.下面是小刚自制“浮力秤”的装置图(如图甲)和使用说明书(如图乙)。
已知“浮力秤”内所装的液体是水,秤盘中未放物体时浮体的圆柱体浸入水中的深度h0为4cm,请根据上述内容和条件解答:
请你完成下列问题:
(1)“浮力秤”能够称出物体的质量,应用原理是始终让浮力秤的浮体处于 (选填“上浮”、“漂浮”或“悬浮”)状态。
(2)根据小刚制作出的“浮力秤”参数可得,秤盘没有放物体时浮体排开水的体积是
cm3,这“浮力秤”的浮体质量是 kg;根据“浮力秤”的使用说明书可知,应把“浮力秤”的刻度刻在 (选填“浮体”或“外筒”)壁上,且刻度是 (选填“均匀”或“不均匀”)的;
(3)理想状态下,使用此“浮力秤”能够达到最大称量值是 kg;达到最大称量时,应在外筒中至少加入 kg的水。
8.物理兴趣小组设计了一个便携式水深测量仪。它主要是由探头A和控制盒B构成,它们之间用有绝缘皮的细导线相连形成回路,如图甲所示。其中探头A是一个底面积为10cm2、高5cm、重2.5N的圆柱体,探头A的底部为压敏电阻R(R与水接触的表面涂有绝缘漆),工作时底部始终与水平面相平,压敏电阻R随表面压力大小的变化如图乙所示。A和B间的电路连接关系如图丙所示,其中电源电压恒为3V,电流表盘改装成深度表(导线的重力与体积均不计)。兴趣小组的同学将探头A缓慢放入水中,求:
(1)探头A刚好全部浸入水中时,R底部受到水的压强是多少Pa?
(2)探头A全部浸入水中时,导线对探头A的拉力是多少N?
(3)将探头投入看似不深的水平池底,静止时(R与池底未紧密结合)导线已松弛,电流表示数是0.4A,则表盘0.4A处应该标水的深度值为多少m?
9.某学习小组,制作了一个探究“滑动摩擦力与压力大小关系”的实验装置,如图甲所示。绝缘的轻质木板,压在硬性轻质且光滑的金属滑片上,木板和金属滑片均水平放置且足够长,电路开关闭合时,可通过改装后的电流表读出滑片所受压力F的大小。重为5.5N的铁块通过细线绕过定滑轮(不计绳重和摩擦),与重为0.5N的空桶相连,将铁块放在水平木板上时,
滑片恰好在滑动变阻器R2底端,电阻不计的弹簧被压缩,此时电路的总功率P=0.6W,R1的功率记为P1。实验装置通过向桶中加入细沙,改变铁块对木板的压力;水平向左推动木板时,铁块始终保持静止,通过始终在水平方向的拉力传感器(位置可随铁块一起相对地面上下调节)的示数,可得出木板与铁块之间摩擦力的大小。电路中,电源电压恒为3V,R2阻值分布均匀(阻值与长度成正比)。弹簧长度变化量与压力的关系如图乙所示。小组实验后,得到压力F压和拉力传感器示数F的数据如表丙所示。
F压/N 0 1 2 3 4 5
F/N 0 0.25 0.5 0.75 1 1.25
(1)若铁块的底面积为20cm2,当F=1N时,铁块对木板的压强为多少?
(2)学习小组应当将电流表的哪个刻度改为压力5N?
(3)若压力为0时,滑片恰好在R2的顶端,此时R1的功率记为P2,且P1:P2=1:9当电流表的示数为0.5A时,向桶中加入细沙的重力为多少?
参考答案
1.解:木条的重力:G=mg=2.4kg×10N/kg=24N;
设木条重心在D点,当C点放在托盘秤甲上,B端放在托盘秤乙上时,以B端为支点,
托盘秤甲的示数是0.8kg,则托盘受到的压力:F压=mCg=0.8kg×10N/kg=8N,
根据力的作用是相互的,所以托盘秤对木条C点的支持力为8N,如图所示:
由杠杆平衡条件有:FC×CB=G×BD,即:8N×CB=24N×BD,
所以:CB=3BD,
因ACAB,所以CBAB
则BDABAB,
CD=AB﹣AC﹣BD=ABABABAB,
欲使乙秤的示数变为0,需将甲秤移到D点,故向右移动的距离为AB。
故选:B。
2.解:因为密度计在使用时始终处于漂浮状态,浮力大小等于重力大小,密度计的重力不变,浮力不变,由阿基米德原理可知,液体密度与密度计浸入液体深度的关系为:ρ液,则液体的密度越大密度计浸入液体深度小,又水的密度大于酒精的密度,所以P与自制密度计静止于水中时的液面重合,Q与自制密度计静止于酒精中时的液面重合;
由ρ液可知,所测液体的密度与密度计浸入液体的深度成反比,液体密度越大,浸入深度越小,所以密度计下端刻度大,并且刻度是不均匀的,上疏下密。当X液体液面位置在PQ中点时,此X液体的密度在水和酒精密度的中点,故此液体密度小于水和酒精密度的平均值,故C正确。
故选:C。
3.解:(1)由杠杆的平衡条件F1l1=F2l2可得m桶g×OA=m秤砣g×OB,即m桶×OA=m秤砣×OB,由于OA>OB,所以m桶<m秤砣;
(2)设桶内装满密度为ρ液的某种液体后,秤砣由B点向右移动到C点,秤杆再次达到平衡状态后,
由杠杆的平衡条件F1l1=F2l2可得:(m桶+m液)g×OA=m秤砣g×(OB+BC),
又m桶g×OA=m秤砣g×OB,
化简得:m液×OA=m秤砣×BC,
又m液=ρ液V液,代入可得:ρ液,由于OA、m秤砣、V液是定值,所以ρ液与BC成正比,即该秤的刻度是均匀的;
(3)把OA=10cm,BC=8cm,m秤砣=100g,V液=100mL=100cm3代入ρ液中可得:ρ液0.8g/cm3=0.8×103kg/m3。
故答案为:(1)>;(2)均匀;(3)0.8×103。
4.解:
(1)取一根粗细均匀的饮料吸管,在其下端内部塞入适量金属丝并用石蜡封口,这样做目的是为了降低重心,让吸管竖直漂浮在液体中;
(2)由于吸管在(a)、(b)图中均漂浮,所以F浮=G,
则在水和另一种液体中受到的浮力相等,F浮水=F浮夜,根据公式F浮=G排=m排g=ρ液gV排得:m1=m2;
由图可知,V排液>V排水,则ρ液<ρ水,
设吸管的底面积为S,根据阿基米德原理F浮=G排=m排g=ρgV排得,ρ水gSH=ρ液gSh,
解得:h;
(3)根据(2)可知,ρ液和h是反比例函数,将上端刻度与下端刻度进行比较,得到刻度线的两个特点是:上端刻度小、下端刻度大,即1.1刻线是在1.0刻线的下方;
(4)①密度计漂浮在液面上时,所受浮力等于其重力;水的密度小于浓盐水的密度,所以在浓盐水中漂浮时,由V排知,密度计排开浓盐水的体积小于排开水的体积,也就是密度计从水中取出放入浓盐水后,会上浮一些。因此只能选择C密度计。
②A、由于密度计C在不同液体中静止时都处于漂浮状态,则F浮=G,即密度计C在不同液体中受到的浮力相等,都等于密度计C受到的重力G,故A错误;
B、密度计C与D是由不同质量的铜丝缠绕在同一规格吸管的外边制成的,由图知,密度计浸入液体的深度相同时,即密度计排开液体的体积相同,由图知,C测量的液体的密度大,根据F浮=ρ液gV排可知:密度计C受到的浮力大,根据漂浮条件可知:密度计C的重力大于D的重力,所以,密度计C上缠绕铜丝的重力大于密度计D上缠绕铜丝的重力,则密度计C上缠绕铜丝的质量大于密度计D上缠绕铜丝的质量,故B错误;
C、密度计C分别测量液体ρ1、ρ2、ρ3时,根据漂浮条件和F浮=ρ液gV排可知密度计C浸入液体的深度分别为:h1,h2;
则密度计C上ρ2与ρ1刻度线的间距:△h21=h1﹣h2;
密度计C上ρ3与ρ2刻度线的间距:△h32=h2﹣h3;
由图知:ρ1<ρ2<ρ3,若ρ3﹣ρ2=ρ2﹣ρ1,则:Δh32:Δh21=( ):( )=ρ1:ρ3<1,所以,△h32<△h21,即:密度计C上ρ3与ρ2刻度线的间距小于ρ2与ρ1刻度线的间距,故C错误。
D、密度计C上ρ3与ρ1刻度线的间距:△h31=h1﹣h3;
同理可得、密度计D分别测量液体ρ1、ρ2、ρ3时,根据漂浮条件和F浮=ρ液gV排可知密度计D浸入液体的深度分别为:
h1′,h2′,h3′;
密度计D上ρ3与ρ1刻度线的间距:△h31′=h1′﹣h3′;
则:Δh31:Δh31′=( ):( )=GC:GD>1,即密度计C上ρ3与ρ1刻度线的间距大于密度计D上ρ3与ρ1刻度线的间距,故D正确。
故选:D。
故答案为:(1)漂浮;(2)=;<; ;(3)下;(4)①C;②D。
5.解:(1)因为当秤盘上不放物体时,小筒漂浮,小筒和秤盘总重G0=1N,
所以此时小筒受到的浮力为:F浮=G0=1N;
(2)根据F浮=ρ液gV排得当秤盘上不放物体时,小筒排开水的体积为:
V排1×10﹣4m3,
由V=Sh得A点距小筒底部的距离:
h5×10﹣3m;
(3)在秤盘上放物体后小筒受到最大浮力为:
F浮′=ρ液gV排′=1.0×103kg/m3×10N/kg×0.02m2×0.2m=40N,
物体的最大重力为:
G=F浮′﹣G0=40N﹣1N=39N,
答:(1)漂浮;此时小筒受到的浮力是1N;
(2)该“浮力秤”的零刻度线应标在小筒上距小筒底部5×10﹣3m处;
(3)该“水秤”模型最大能称量的物体重量为39N。
6.解:(a)木料的体积:
V=Sh=0.1m2×0.4m=0.04m3,
由ρ可得,木料的质量:
m=ρV=0.5×103kg/m3×0.04m3=20kg,
(b)木料的重力:
G=mg=20kg×10N/kg=200N,
因木料静止时处于漂浮状态,受到的浮力和自身的重力相等,
由F浮=ρgV排可得,木料排开水的体积:
V排0.02m3,
木料浸入深度:
h0.2m;
(c)当木料上放置某物体时,木料排开水的体积:
V排′=S(h﹣h′)=0.1m2×(0.4m﹣0.1m)=0.03m3,
木料和物体受到的浮力:
F浮′=ρ水gV排′=1.0×103kg/m3×10N/kg×0.03m3=300N,
因木料和物体整体处于漂浮状态,
所以,木料和物体的总重力G总=F浮′=300N,
则物体的重力:
G′=F浮′﹣G=300N﹣200N=100N,
对应称量物体的质量:
m′10kg。
答:(a)木料的质量是20kg;
(b)当木料上不放置任何物体时,木料浸入深度为0.2m;
(c)当木料上放置某物体时,对应称量物体的质量为10kg。
7.解:(1)“浮力秤”能够称出物体的质量,应用原理是漂浮的物体,所受的浮力等于自身的重力;
(2)秤盘没有放物体时浮体排开水的体积是:V排=Sh=250cm2×4cm=1000cm3;
浮体的浮力和重力分别用F浮1和G0表示,
浮体漂浮可得浮体重力:G0=F浮1=ρ水gV排1=1.0×103kg/m3×10N/kg×1000×10﹣6m3=10N,
浮体的质量:m01kg;
由说明可知,浮力秤是根据浮体在水中浸入的深度读数的,所以刻度线应刻在浮体上;
秤盘中未放物体时,浮体在水中漂浮,则有
F浮1=G0
ρ水gV排1=G0
化简后可得:G0=Sρ水gh0;=
被秤物体放在秤盘上后,浮体仍漂浮,则有
F浮2=G0+G物
ρ水gV排2=G0+mg
ρ水gSh=ρ水gSρh0+mg
化简后可得:m=Sρ水(h﹣h0);此式中,S、ρ水、h0均为定值,由此可知,m与h为一次函数,所以刻度是均匀的。
(3)由图可知,浮体的最大长度为40cm,能称得的最大质量:
m大=Sρ水(h﹣h0)=250×10﹣4m2×1.0×103kg/m3×(40﹣4)×10﹣2m=9kg;
达到最大称量时,应在外筒中加入水的体积:
V水=V容﹣V浮体=300×40×10﹣6m3﹣250×40×10﹣6m3=2×10﹣3m3,
水的质量:m水=ρ水V水=1.0×103kg/m3×2×10﹣3m3=2kg。
故答案为:(1)漂浮;(2)1000;1;浮体;均匀;(3)9;2。
8.解:(1)探头A刚好全部浸入水中时,R底部的深度:h=5cm=0.05m,
R底部受到水的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(2)探头A全部浸入水中时,排开水的体积:V排=V=Sh=10cm2×5cm=50cm3=5×10﹣5m3,
受到的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×5×10﹣5m3=0.5N,
探头A处于平衡状态,由F浮=G﹣F′可得,导线对探头A的拉力:
F′=G﹣F浮=2.5N﹣0.5N=2N;
(3)由图丙可知,电路为压敏电阻R的简单电路,电流表测电路中的电流,
当电流表示数是0.4A时,由I可得,R的阻值:
R7.5Ω,
由图乙可知,压敏电阻R表面受到的压力F=75N,
探头A受到池底的支持力:
F支持=G﹣F浮=2.5N﹣0.5N=2N,
水对A底部的压力:
F水压=F﹣F支持=75N﹣2N=73N,
则压敏电阻受到水的压强:
p′7.3×104Pa,
水的深度:
h′7.3m,
所以,表盘0.4A处应该标水的深度值为7.3m。
答:(1)探头A刚好全部浸入水中时,R底部受到水的压强是500Pa;
(2)探头A全部浸入水中时,导线对探头A的拉力是2N;
(3)表盘0.4A处应该标水的深度值为7.3m。
9.解:(1)由表格可知当F=1N时,木板受到的压力F压=4N,铁块对木板的压强:p2000Pa;
(2)重为5.5N的铁块通过细线绕过定滑轮(不计绳重和摩擦),与重为0.5N的空桶相连,将铁块放在水平木板上时,滑片恰好在滑动变阻器R2底端,
此时铁块受到的压力:F压1=G铁块﹣G桶=5.5N﹣0.5N=5N,
此时定值电阻和滑动变阻器的最大电阻串联接入电路,电路的总功率P=0.6W,
通过电路的电流:I0.2A,
所以应当将电流表0.2A的刻度改为压力5N;
(3)定值电阻和滑动变阻器的最大电阻串联接入电路时,R1的功率记为P1,则P1=I2R1=(0.2A)2×R1,
压力为0时,滑片恰好在R2的顶端,此时电路为定值电阻的简单电路,此时R1的功率记为P2,则P2,
已知P1:P2=1:9,即,解方程可得R1=5Ω,
当电流表的示数为0.5A时,根据欧姆定律可得此时电路总电阻:R′6Ω,
串联电路总电阻等于各部分电阻之和,则滑动变阻器接入电路的阻值:R2=R′﹣R1=6Ω﹣5Ω=1Ω,
定值电阻和滑动变阻器的最大电阻串联接入电路时,电路总电阻:R15Ω,
滑动变阻器的最大阻值:R2=R﹣R1=15Ω﹣5Ω=10Ω,
由图乙可知弹簧的最大伸长量为5cm,弹簧受到的最大压力为5N,所以滑动变阻器的长度为5cm,
当电流表的示数为0.5A时,铁块受到的压力F压′5cm4.5N,
空桶和沙子的总重力:G=G铁块﹣F压′=5.5N﹣4.5N=1N,
向桶中加入细沙的重力为:G沙子=G﹣G桶=1N﹣0.5N=0.5N。
答:(1)若铁块的底面积为20cm2,当F=1N时,铁块对木板的压强为2000Pa;
(2)学习小组应当将电流表0.2A的刻度改为压力5N;
(3)当电流表的示数为0.5A时,向桶中加入细沙的重力为0.5N。
物理仪器原理探究
同课章节目录
