人教版九年级上册 23.1 图形的旋转 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级上册 23.1 图形的旋转 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
图形的旋转
23.1.1
温故知新
问题1 我们已经学习过哪些图形的变换的方式?
平移,轴对称
追问1 主要研究了它们的哪些方面?
定义,性质,应用(画图、坐标表示等)
追问2 平移和轴对称的定义是怎样得出的?
引出概念
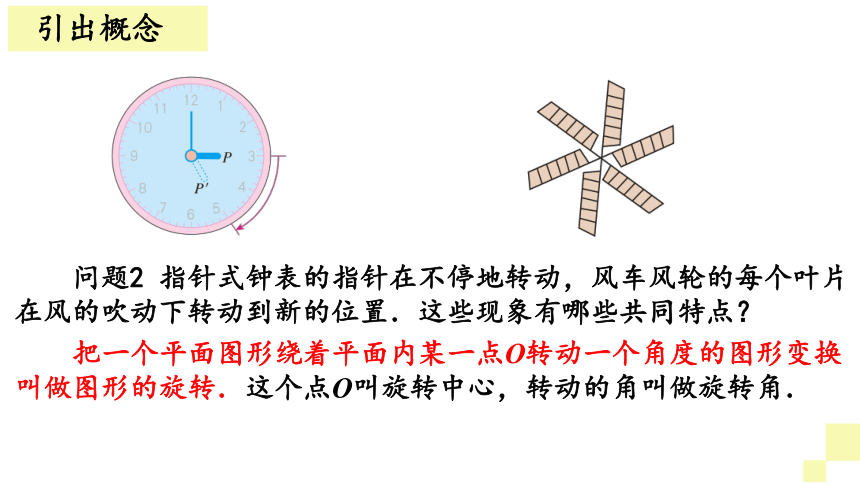
问题2 指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.
应用概念
1.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
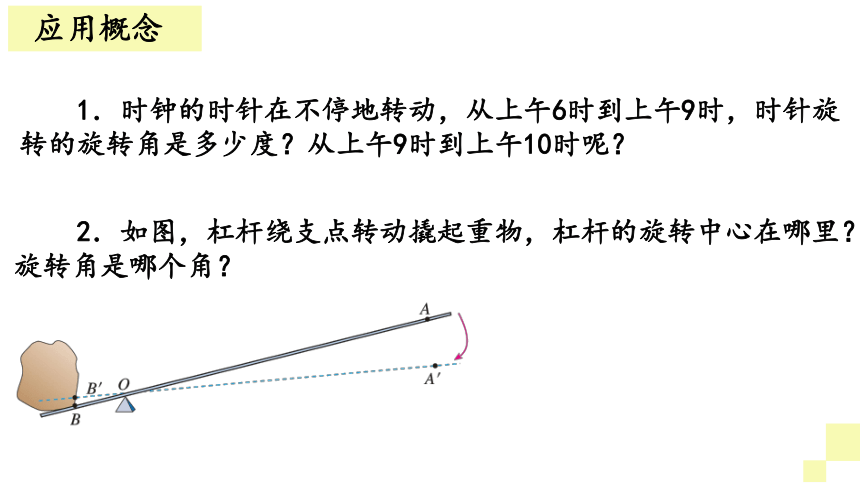
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
合作探究
问题3 类比平移和轴对称,旋转有哪些特性,体现在哪些方面?
1.图形变化前后的形状、大小之间的关系;
2.对应点间的数量和位置关系;
整体
局部
合作探究
问题4 在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'B'C'),移开硬纸板.请同学们思考以下问题:
(1)△A'B'C'可以看作△ABC经过怎样的运动得到的?
绕着点O旋转得到
旋转性质1:形状和大小完全相同
(2)△ABC和△A'B'C'的形状和大小有什么关系?
合作探究
问题4 在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'B'C'),移开硬纸板.请同学们思考以下问题:
旋转性质2:对应点到旋转中心的距离相等.
(3)△ABC和△A'B'C'的对应点之间有何数量和位置上的特征?
旋转性质3:对应点与旋转中心所连线段的夹角等于旋转角.
归纳小结
问题5 结合平移与轴对称,你能说一下旋转变换研究的策略吗?
旋转
平移,轴对称
类比
性质
定义
观察
猜想
画图
研究内容
研究思路
研究方法
性质(图形变化中的不变性或要素与要素间的关系)
应用
验证
新知应用
例1:下图为4×4的正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°,你能画出△OAB旋转后的图△O'A'B'吗?
A
B
O
新知应用
例2:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
总结:利用旋转的性质作图,图形的旋转可转化为点的旋转.
图形的旋转(第1课时)教学阐述
23.1.1
一.学情分析
1.小学的学习,学生对于旋转已有一定的认识.;
2.七、八年级时,学生已经学移和轴对称两种图形的变换.
二.教材解读
1. 旋转是一种基本的图形变化,且是全等变换.
2. 学生对图形之间关系的认识从静态上升到动态.
三.目标定位与基本理念
1.通过观察具体实例认识旋转,归纳旋转的概念.
2.探索旋转的性质,会画出旋转后的图形.
四.教学重、难点
教学重点:旋转的性质.
教学难点:“对应点到旋转中学的夹角相等”性质的发现.
五.方法选择
在教师引导下找到归纳性质的线索,并逐步构建起探究的思路. 在教学过程中不断地进行引导和渗透,使学生不断感悟、领会,逐步养成几何研究的一般方法.
六.课程设计
研究方法:画图——观察——猜想——验证
研究思路:背景——概念——分离要素——性质——应用
研究内容:性质(图形变化中的不变性或要素与要素间的关系)
全等变换的研究策略:
图形的旋转
23.1.1
温故知新
问题1 我们已经学习过哪些图形的变换的方式?
平移,轴对称
追问1 主要研究了它们的哪些方面?
定义,性质,应用(画图、坐标表示等)
追问2 平移和轴对称的定义是怎样得出的?
引出概念
问题2 指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.
应用概念
1.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?
2.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
合作探究
问题3 类比平移和轴对称,旋转有哪些特性,体现在哪些方面?
1.图形变化前后的形状、大小之间的关系;
2.对应点间的数量和位置关系;
整体
局部
合作探究
问题4 在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'B'C'),移开硬纸板.请同学们思考以下问题:
(1)△A'B'C'可以看作△ABC经过怎样的运动得到的?
绕着点O旋转得到
旋转性质1:形状和大小完全相同
(2)△ABC和△A'B'C'的形状和大小有什么关系?
合作探究
问题4 在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'B'C'),移开硬纸板.请同学们思考以下问题:
旋转性质2:对应点到旋转中心的距离相等.
(3)△ABC和△A'B'C'的对应点之间有何数量和位置上的特征?
旋转性质3:对应点与旋转中心所连线段的夹角等于旋转角.
归纳小结
问题5 结合平移与轴对称,你能说一下旋转变换研究的策略吗?
旋转
平移,轴对称
类比
性质
定义
观察
猜想
画图
研究内容
研究思路
研究方法
性质(图形变化中的不变性或要素与要素间的关系)
应用
验证
新知应用
例1:下图为4×4的正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°,你能画出△OAB旋转后的图△O'A'B'吗?
A
B
O
新知应用
例2:如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,你能画出旋转后的图形吗?试一试你有几种方法?
A
B
C
E
D
总结:利用旋转的性质作图,图形的旋转可转化为点的旋转.
图形的旋转(第1课时)教学阐述
23.1.1
一.学情分析
1.小学的学习,学生对于旋转已有一定的认识.;
2.七、八年级时,学生已经学移和轴对称两种图形的变换.
二.教材解读
1. 旋转是一种基本的图形变化,且是全等变换.
2. 学生对图形之间关系的认识从静态上升到动态.
三.目标定位与基本理念
1.通过观察具体实例认识旋转,归纳旋转的概念.
2.探索旋转的性质,会画出旋转后的图形.
四.教学重、难点
教学重点:旋转的性质.
教学难点:“对应点到旋转中学的夹角相等”性质的发现.
五.方法选择
在教师引导下找到归纳性质的线索,并逐步构建起探究的思路. 在教学过程中不断地进行引导和渗透,使学生不断感悟、领会,逐步养成几何研究的一般方法.
六.课程设计
研究方法:画图——观察——猜想——验证
研究思路:背景——概念——分离要素——性质——应用
研究内容:性质(图形变化中的不变性或要素与要素间的关系)
全等变换的研究策略:
同课章节目录
