数形结合思想在解题中的应用[下学期]

课件14张PPT。数形结合思想在解题中的运用崇信县第一中学 尹军民
2019年3月15日引入语在数学解题中，方法至关重要，这对于节省时间，提高效率，煅炼能力有重要的作用.常用的数学思想方法主要包括：数形结合思想、转化思想、分类讨论思想，方程与函数的思想.这里简要谈谈数形结合思想.“数缺形来少直观，形缺数来难入微”可见数、形间相互联系，它们相辅相成，成为解决的数学问题的重要方法。用图形来帮助理解数学问题，已经成为当今数学的特色之一. 正文
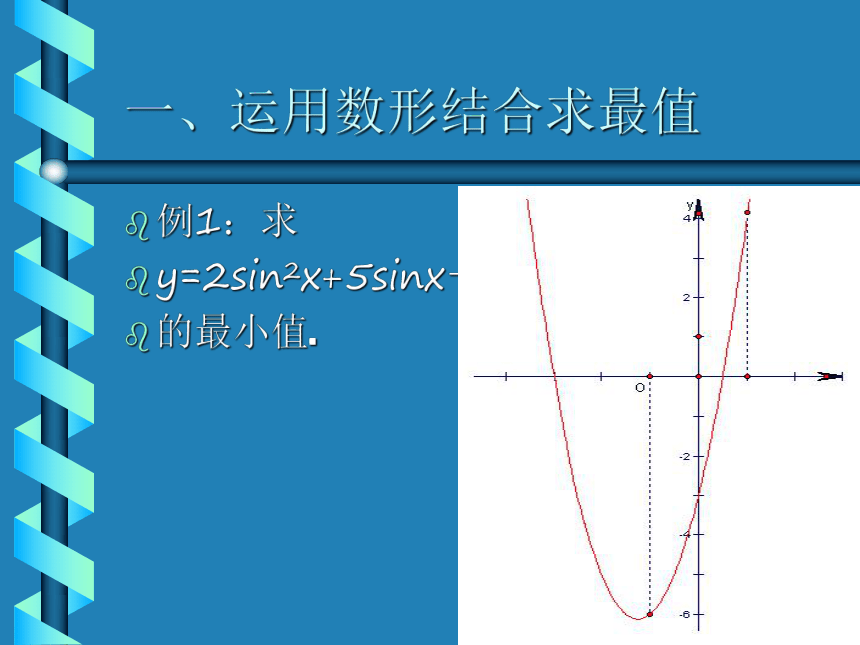
下面通过几道典型例题进行简要分析，请大家一起来品味数形结合思想在数学解题中的妙用。一、运用数形结合求最值例1：求
y=2sin2x+5sinx－3
的最小值.一、运用数形结合求最值解：如图所示,由于－1≤sinx≤1可知当sinx=－1时，y取得最小值，ymin=－6.
平常解题中容易犯错，误 以为顶点的纵坐标为最大值，通过图象就不易犯错了.
二、利用数形结合求取值范围例2：求log2(－x)解：如图,画出
y=log2 (－x)，
y=x+1的图象，
容易得出x的
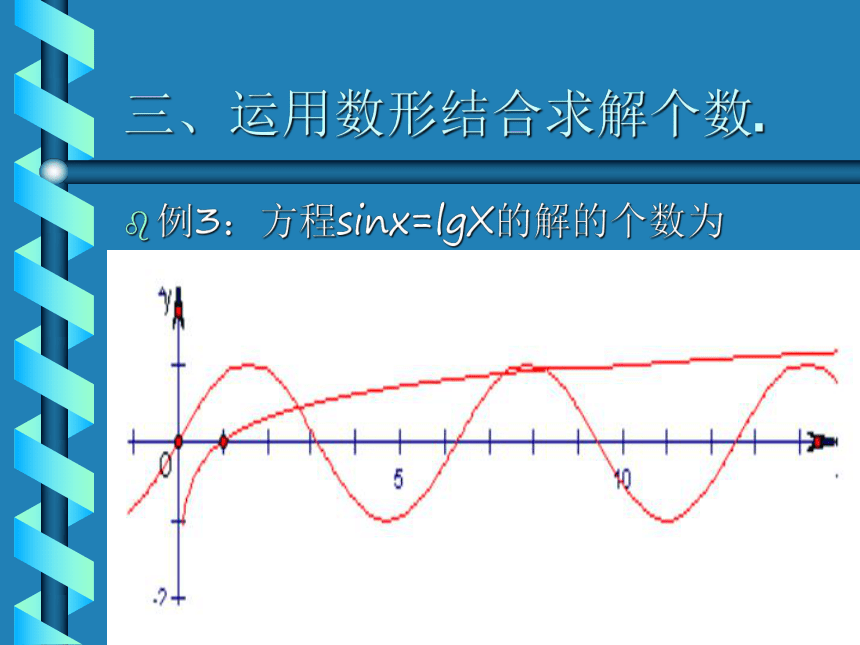
范围为（－1，0）三、运用数形结合求解个数.例3：方程sinx=lgX的解的个数为______.三、运用的形结合求解个数.解：如图所示，显然当x=10时lgx=1，
而当x=　π<10时，y=sinx=1，容易得知，
sin　π>lg　π∴y=sinx与y=lgx在[2π,3π]有2个交点，加上[0，π]的一个交点，共3个交点，而在[3π，+∞)中不可能有交点，∴方程解的个数为3个四、运用数形结合求关系式例4：已知7a=0.9，0.7b=0.6，判断ab与0的大小.
四、运用数形结合求关系式
解：画出y=7a与y=0.7b的图象显然，
a>0，b<0
∴ab<0.四、运用数形结合求关系式例5：设a、b、c分别是方程2x+x=1，2x+x=2，3x+x=2的根，则a，b，c的大小顺序为______ .四、运用数形结合求关系式解：由题意可知
2x=1 －x，2x=2 －x，3x=2 －x
分别作出y=2x，y=3x，y=1－x，y=2－x的图象，则y=2x与y=1－x图象交点的横坐标为a ，同理可得b，c.
由图象可知a