【新课标】6.1.2 平行四边形的性质 课件(21张PPT)
文档属性
| 名称 | 【新课标】6.1.2 平行四边形的性质 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 14:49:16 | ||
图片预览


文档简介
(共21张PPT)
6.1.2 平行四边形的性质
北师版八年级下册
教学目标
1.理解并掌握平行四边形对角线互相平分的性质,综合运用平行四边形的性质.
2.通过观察图形,发现平行四边形的性质并证明.
3.通过探索、观察、分析,实现知识的迁移与转化.
新知导入
A
B
C
D
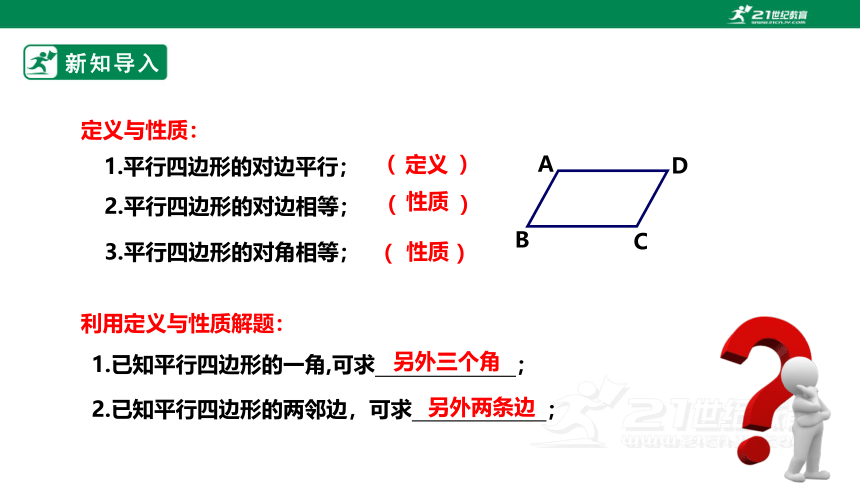
定义与性质:
1.平行四边形的对边平行;
( )
定义
2.平行四边形的对边相等;
( )
性质
3.平行四边形的对角相等;
( )
性质
利用定义与性质解题:
1.已知平行四边形的一角,可求 ;
另外三个角
2.已知平行四边形的两邻边,可求 ;
另外两条边
探究新知
●
A
D
O
C
B
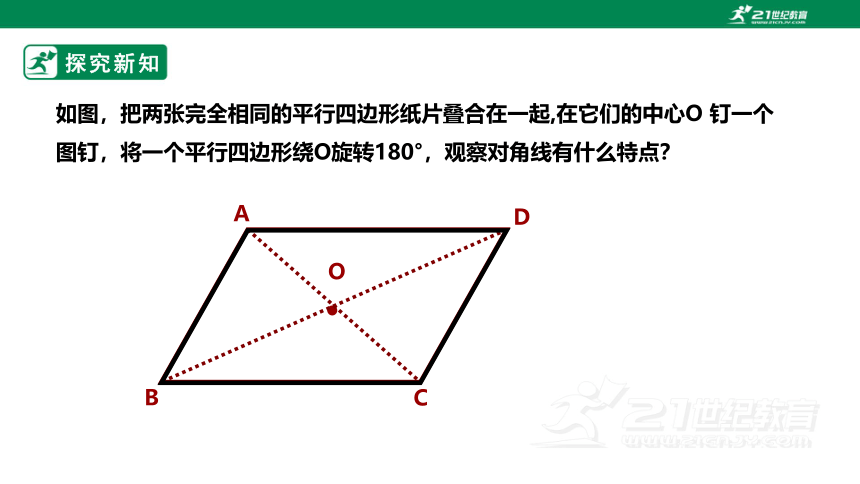
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,观察对角线有什么特点?
探究新知
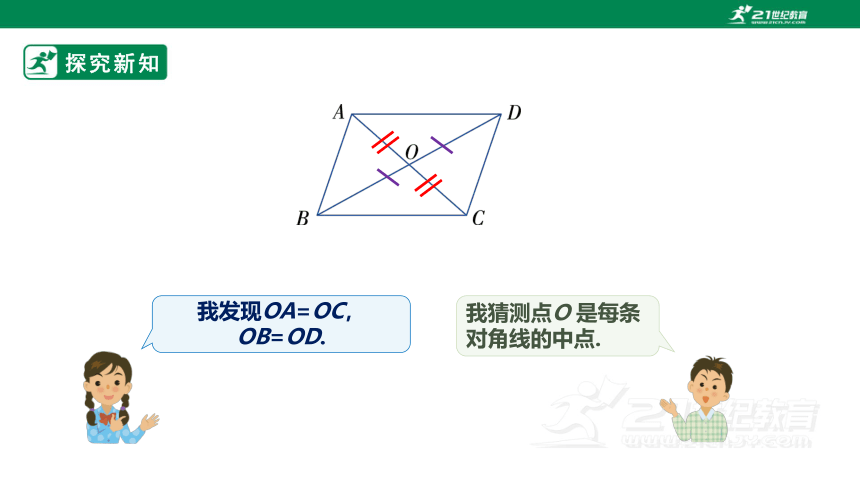
我发现OA=OC,OB=OD.
我猜测点O 是每条对角线的中点.
探究新知
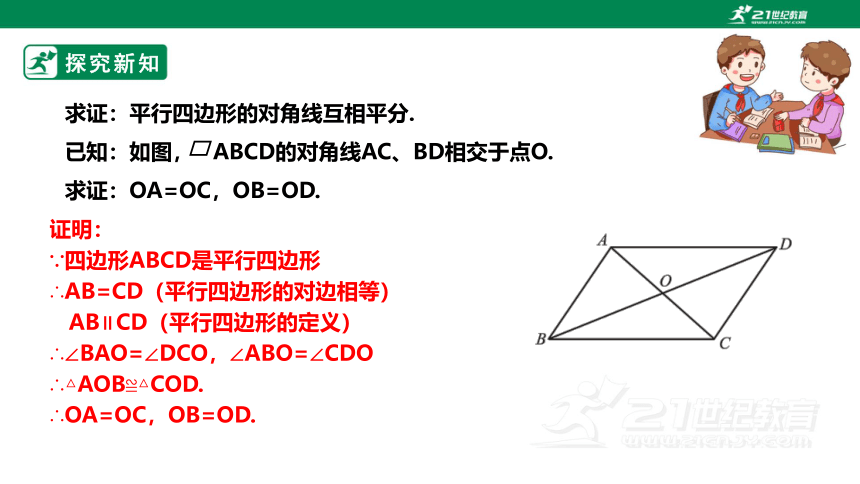
已知:如图, ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
求证:平行四边形的对角线互相平分.
证明:
∵四边形ABCD是平行四边形
∴AB=CD(平行四边形的对边相等)
AB∥CD(平行四边形的定义)
∴∠BAO=∠DCO,∠ABO=∠CDO
∴△AOB≌△COD.
∴OA=OC,OB=OD.
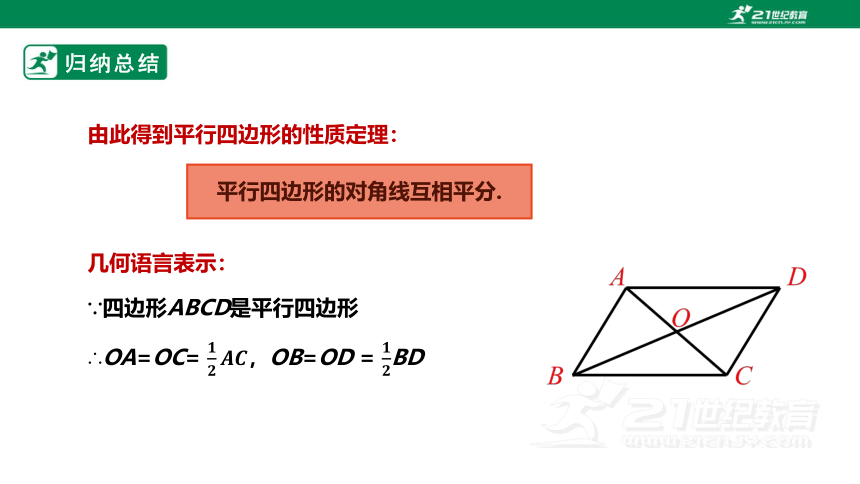
归纳总结
几何语言表示:
由此得到平行四边形的性质定理:
平行四边形的对角线互相平分.
∵四边形ABCD是平行四边形
∴OA=OC= ,OB=OD = BD
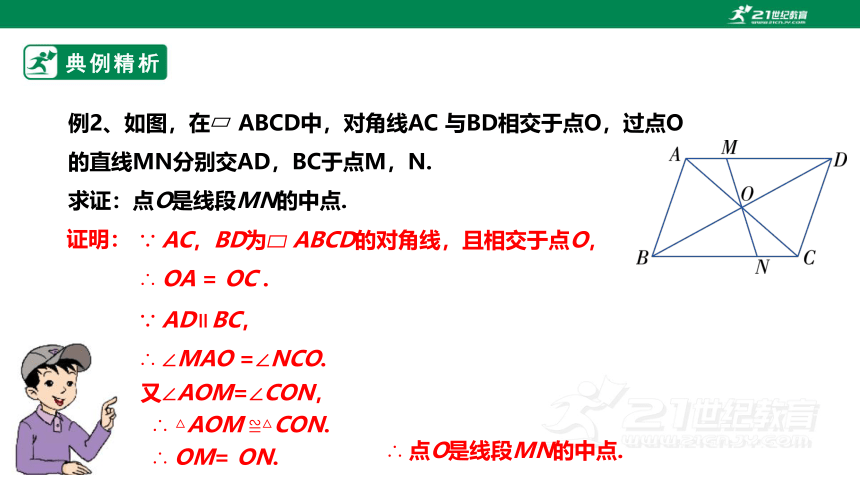
典例精析
例2、如图,在 ABCD中,对角线AC 与BD相交于点O,过点O的直线MN分别交AD,BC于点M,N.
求证:点O是线段MN的中点.
∵ AD∥BC,
∴ ∠MAO =∠NCO.
又∠AOM=∠CON,
∴ △AOM ≌△CON.
∴ OM= ON.
∵ AC,BD为ABCD的对角线,且相交于点O,
∴ OA = OC .
证明:
∴ 点O是线段MN的中点.
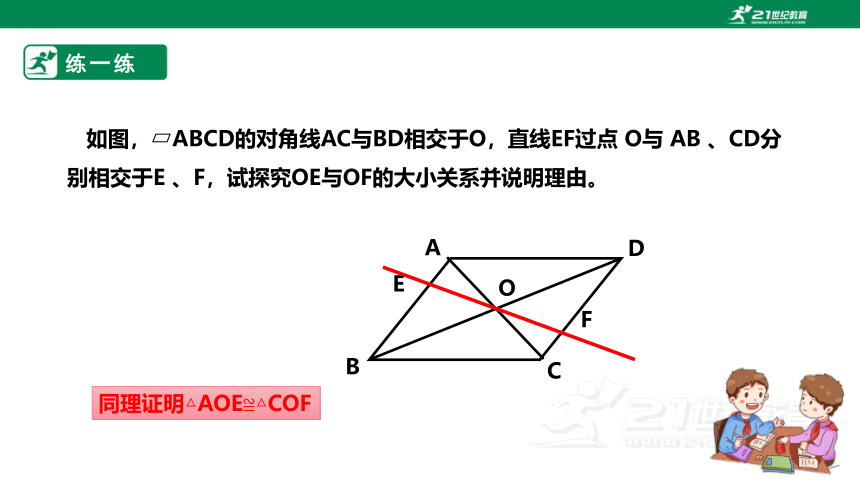
练一练
如图, ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
同理证明△AOE≌△COF
归纳总结
1 . △ABO ≌ △CDO, △AOD ≌ △COB,
△ ABD ≌ △CDB,△ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
做一做
如图, ABCD的对角线AC与BD相交于点O,∠ADB=90°,OA=6,OB=3.求AD和AC的长度.
解:∵四边形ABCD是平行四边形,
∴OA=OC=6,OB=OD=3
(平行四边形的对角线互相平分),
∴AC=OA+OC=12,
∵ ∠ADB=90°.
∴△ADO为直角三角形.
∴AD== .
课堂练习
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角和为360度 D、外角和为360度
B
2.在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是( )
A. 24C.7B
C
D
A
O
C
课堂练习
3、如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
4.如图,在平行四边形ABCD中,∠A=150°,AB=8cm,BC=10cm,平行四边形ABCD的面积为 .
40cm2
D
B
A
C
课堂练习
5、如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O且与AB,CD 分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC 的周长是10,求 ABCD 的周长.
课堂练习
∵四边形ABCD 是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO 和△BEO 中,
∴△DFO ≌ △BEO (ASA).
∴OE=OF.
(1)证明:
课堂练习
∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC 的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10.
∴ ABCD 的周长=2(BC+AB )=20.
(2)解:
课堂总结
平行四边形的对角线互相平分.
平行四边形的对边平行且相等;
性质1:
平行四边形的对角相等.
性质2:
性质3:
板书设计
课题:6.1.2平行四边形的性质
性质
(1)边
(2)角
(3)对角线
作业布置
【必做题】
教材139页练习题1、2题
【选做题】
教材139页练习题3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.1.2 平行四边形的性质
北师版八年级下册
教学目标
1.理解并掌握平行四边形对角线互相平分的性质,综合运用平行四边形的性质.
2.通过观察图形,发现平行四边形的性质并证明.
3.通过探索、观察、分析,实现知识的迁移与转化.
新知导入
A
B
C
D
定义与性质:
1.平行四边形的对边平行;
( )
定义
2.平行四边形的对边相等;
( )
性质
3.平行四边形的对角相等;
( )
性质
利用定义与性质解题:
1.已知平行四边形的一角,可求 ;
另外三个角
2.已知平行四边形的两邻边,可求 ;
另外两条边
探究新知
●
A
D
O
C
B
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,观察对角线有什么特点?
探究新知
我发现OA=OC,OB=OD.
我猜测点O 是每条对角线的中点.
探究新知
已知:如图, ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
求证:平行四边形的对角线互相平分.
证明:
∵四边形ABCD是平行四边形
∴AB=CD(平行四边形的对边相等)
AB∥CD(平行四边形的定义)
∴∠BAO=∠DCO,∠ABO=∠CDO
∴△AOB≌△COD.
∴OA=OC,OB=OD.
归纳总结
几何语言表示:
由此得到平行四边形的性质定理:
平行四边形的对角线互相平分.
∵四边形ABCD是平行四边形
∴OA=OC= ,OB=OD = BD
典例精析
例2、如图,在 ABCD中,对角线AC 与BD相交于点O,过点O的直线MN分别交AD,BC于点M,N.
求证:点O是线段MN的中点.
∵ AD∥BC,
∴ ∠MAO =∠NCO.
又∠AOM=∠CON,
∴ △AOM ≌△CON.
∴ OM= ON.
∵ AC,BD为ABCD的对角线,且相交于点O,
∴ OA = OC .
证明:
∴ 点O是线段MN的中点.
练一练
如图, ABCD的对角线AC与BD相交于O,直线EF过点 O与 AB 、CD分别相交于E 、F,试探究OE与OF的大小关系并说明理由。
A
B
C
D
O
E
F
同理证明△AOE≌△COF
归纳总结
1 . △ABO ≌ △CDO, △AOD ≌ △COB,
△ ABD ≌ △CDB,△ ABC ≌ △CDA ;
2. △ABO、 △AOD、 △DOC、 △COB的面积相等,且都等于平行四边形面积的四分之一.
做一做
如图, ABCD的对角线AC与BD相交于点O,∠ADB=90°,OA=6,OB=3.求AD和AC的长度.
解:∵四边形ABCD是平行四边形,
∴OA=OC=6,OB=OD=3
(平行四边形的对角线互相平分),
∴AC=OA+OC=12,
∵ ∠ADB=90°.
∴△ADO为直角三角形.
∴AD== .
课堂练习
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角和为360度 D、外角和为360度
B
2.在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是( )
A. 24
C
D
A
O
C
课堂练习
3、如图,在 ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
5
4.如图,在平行四边形ABCD中,∠A=150°,AB=8cm,BC=10cm,平行四边形ABCD的面积为 .
40cm2
D
B
A
C
课堂练习
5、如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O且与AB,CD 分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC 的周长是10,求 ABCD 的周长.
课堂练习
∵四边形ABCD 是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO 和△BEO 中,
∴△DFO ≌ △BEO (ASA).
∴OE=OF.
(1)证明:
课堂练习
∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC 的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10.
∴ ABCD 的周长=2(BC+AB )=20.
(2)解:
课堂总结
平行四边形的对角线互相平分.
平行四边形的对边平行且相等;
性质1:
平行四边形的对角相等.
性质2:
性质3:
板书设计
课题:6.1.2平行四边形的性质
性质
(1)边
(2)角
(3)对角线
作业布置
【必做题】
教材139页练习题1、2题
【选做题】
教材139页练习题3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
