【备考2023】浙教版科学“冲刺重高”压轴训练(三十八):杠杆的应用(含解析)
文档属性
| 名称 | 【备考2023】浙教版科学“冲刺重高”压轴训练(三十八):杠杆的应用(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 596.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-05-19 00:30:49 | ||
图片预览



文档简介
1.如图所示,AOB是一杠杆(自重不计,O为支点,OA<0B OD=OA),在A端悬挂一重物G,那么( )
A.在B点用力使杠杆在图示位置平衡,一定是省力的
B.在C点用力不可能使杠杆在图示位置平衡
C.在B点用力使杠杆在图示位置平衡,沿竖直方向最省力
D.在D点悬挂一个与G完全相同的物体能使杠杆在图示位置平衡
2.小华在做实验时提出了如图所示两个模型,两杠杆均处于平衡状态,甲杠杆上平衡的是两个密度相同但体积不同的实心物体,乙杠杆上平衡的是两个体积相同但密度不同的实心物体(物体的密度都大于水)。如果将它们都浸没在水中,则两杠杆将( )
A.仍保持平衡 B.都失去平衡
C.甲仍保持平衡,乙失去平衡 D.甲失去平衡,乙仍保持平衡
3.如图所示,一轻质杠杆AB支在支架上,OA=20cm,G1为一边长为5cm的正方体,G2重为20N.当OC=10cm时,G1对地面的压强为2×104Pa。现用一水平拉力F使G2以2cm/s的速度向右匀速运动,则当G1对地面的压力为0时所经过的时间为 ( )
A.25s B.30s C.35s D.40s
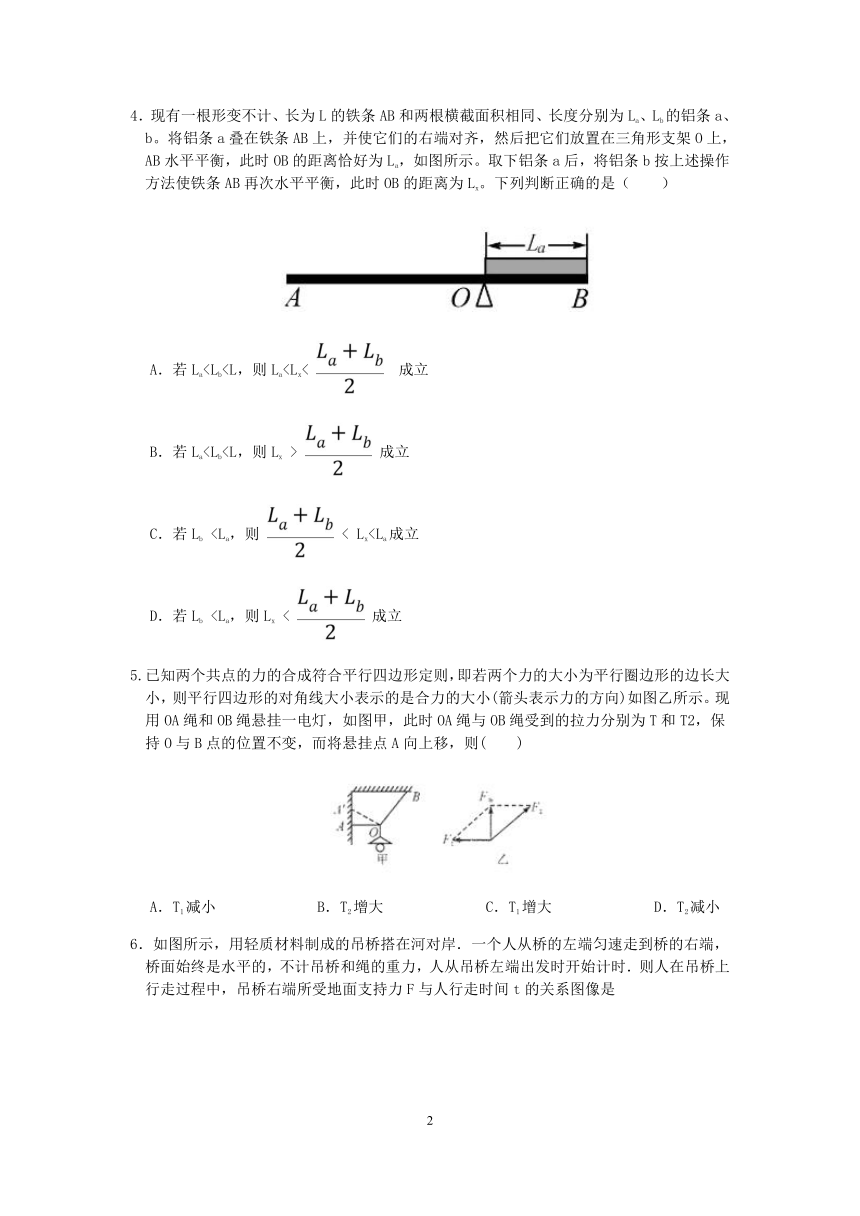
4.现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b。将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡,此时OB的距离为Lx。下列判断正确的是( )
A.若LaB.若La 成立
C.若LbD.若Lb 5.已知两个共点的力的合成符合平行四边形定则,即若两个力的大小为平行圈边形的边长大小,则平行四边形的对角线大小表示的是合力的大小(箭头表示力的方向)如图乙所示。现用OA绳和OB绳悬挂一电灯,如图甲,此时OA绳与OB绳受到的拉力分别为T和T2,保持O与B点的位置不变,而将悬挂点A向上移,则( )
A.T1减小 B.T2增大 C.T1增大 D.T2减小
6.如图所示,用轻质材料制成的吊桥搭在河对岸.一个人从桥的左端匀速走到桥的右端,桥面始终是水平的,不计吊桥和绳的重力,人从吊桥左端出发时开始计时.则人在吊桥上行走过程中,吊桥右端所受地面支持力F与人行走时间t的关系图像是
A.B.C.D.
7.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中( )
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确 B.只有②③正确
C.只有①②正确 D.只有③④正确
8.小金推着购物车在超市购物,如右图所示,购物车和货物的总重为100N,A点离地面距离为0.8m,B、C点为车轮与地面的接触点,当购物车前轮遇到障碍物时,小金先后在A点对购物车施加了最小作用力。在使车的前轮越过障碍物时,施加的最小力的方向为 ,最小力的大小为 N;此时购物车可视为 杠杆(选“省力”“费力”“等臂”)。
9.如图装置为科技创新大赛时发明的可以直接测量液体密度的“密度天平”。其制作过程和原理如下:选择一根长1.2米的均匀杠杆,支点在其中点,调节两边螺母使杠杆在水平位置平衡,在左侧离中点10厘米的位置用细线固定一个质量为 120 克、容积为80毫升的容器,右侧用细线悬挂一质量为40克的钩码(细线的质量忽略不计)。测量时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位置直接读出液体的密度。
(1)该“密度天平”的“零刻度”应标在右端离支点 厘米处;
(2)该“密度天平”的最大刻度值为 kg/m3;
(3)若将钩码的质量适当增大,该“密度天平”的量程将 (选填“增大”、“减小”或“不变”) ;(4)该“密度天平”的刻度是 的(“均匀”、“不均匀”)
10.如图所示,一均匀木条可绕转轴O自由转动,现有材料相同,长度相同,横截面积之比Sa:Sb:Sc=1:4:2的三支蜡烛a、b、c,垂直立于木条上,木条恰好处于平衡。三支蜡烛离转轴的距离分别为L1、L2和L3,若L1=4L2,则L3= L2。若同时点燃蜡烛蜡烛在燃烧过程中,要使杠杆保持平衡,则L1:L2:L3= (蜡烛在相等时间内燃烧的质量相同)。
11.如图所示,质量为m的人站在质量为的均匀木板AB的中点,木板可以绕B端转动,2若以人的重力为动力,这属于 (选填“省力”或“费力”)杠杆。要使木板处于水平状态不动,此人拉力的大小为 。(摩擦忽略不计)
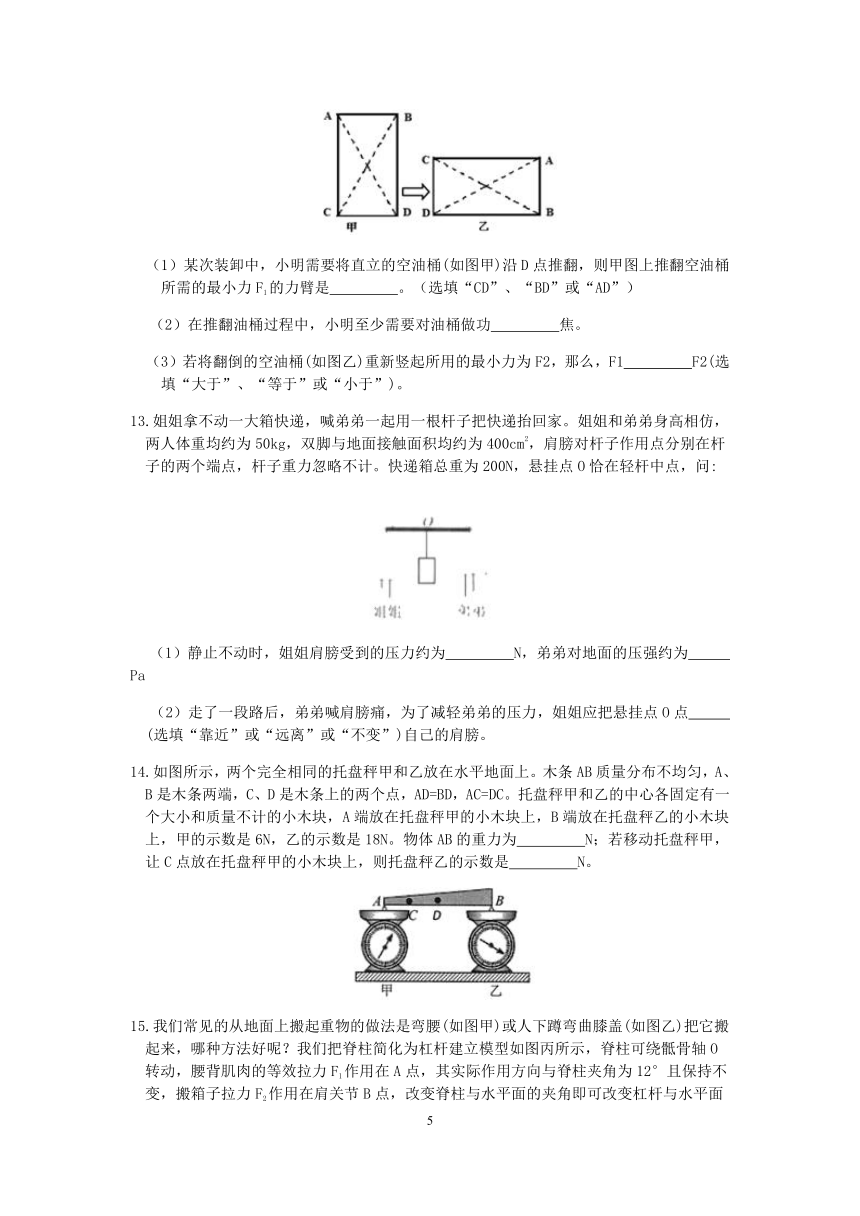
12.如图为油厂的油桶,空桶质量为65Kg,油桶高为1.2m,底部直径为0.5m,据此回答。
(1)某次装卸中,小明需要将直立的空油桶(如图甲)沿D点推翻,则甲图上推翻空油桶所需的最小力F1的力臂是 。(选填“CD”、“BD”或“AD”)
(2)在推翻油桶过程中,小明至少需要对油桶做功 焦。
(3)若将翻倒的空油桶(如图乙)重新竖起所用的最小力为F2,那么,F1 F2(选填“大于”、“等于”或“小于”)。
13.姐姐拿不动一大箱快递,喊弟弟一起用一根杆子把快递抬回家。姐姐和弟弟身高相仿,两人体重均约为50kg,双脚与地面接触面积均约为400cm2,肩膀对杆子作用点分别在杆子的两个端点,杆子重力忽略不计。快递箱总重为200N,悬挂点O恰在轻杆中点,问:
(1)静止不动时,姐姐肩膀受到的压力约为 N,弟弟对地面的压强约为 Pa
(2)走了一段路后,弟弟喊肩膀痛,为了减轻弟弟的压力,姐姐应把悬挂点O点 (选填“靠近”或“远离”或“不变”)自己的肩膀。
14.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上。木条AB质量分布不均匀,A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。托盘秤甲和乙的中心各固定有一个大小和质量不计的小木块,A端放在托盘秤甲的小木块上,B端放在托盘秤乙的小木块上,甲的示数是6N,乙的示数是18N。物体AB的重力为 N;若移动托盘秤甲,让C点放在托盘秤甲的小木块上,则托盘秤乙的示数是 N。
15.我们常见的从地面上搬起重物的做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?我们把脊柱简化为杠杆建立模型如图丙所示,脊柱可绕骶骨轴O转动,腰背肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论。
(1)当α角增大时,F1如何变化?并说明理由。
(2)比较甲、乙两种姿势所对应丙图中的两种状态,分析可得, (选填“甲”或“乙”)图中的姿势比较正确。
16.某同学要测一个金属块的密度,他手中的测量工具只有一只量程较小的弹簧测力计,当他用此弹簧测力计测量该金属块的重力时,发现已超过弹簧测力计的最大量程,于是他设计了如图所示的装置去测量。图中OA:OB=1:3。他实验的步骤如下:
⑴用细绳把金属块悬挂于A点,用弹簧测力计在B点作用一个竖直向上的力,使杠杆OAB在水平位置静止,金属块静止在空中,读出弹簧测力计此时的读数F1;
⑵向容器中加适量的水,“适量”指的是 ,待杆在水平位置重新平衡后,再读出弹簧测力计此时的读数F2,则F1 F2(选填“大于”、“等于”、“小于”);
⑶若杠杆OAB质量不计,则被测金属块密度的表达式:ρ= 。(水的密度表示为ρ水)
17.某同学制作了直接测量液体密度的“密度天平”.其制作过程和原理如下:如图甲所示,选择一个长杠杆,调节两边螺母使杠杆在水平位罝平衡;在左侧离支点10cm的位罝A用细线固定一个质量为110g、容积为50mL的容器.右侧用细线悬挂一质量为50g的钩码(细线的质量忽略不计)。
【测量过程】将下对实验空白处补充完整:
(1)调节杠杆平衡时,发现杠杆左端下沉,需将平衡螺母向 端调节(填“左”或“右”);测量液体时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位罝直接读出液体密度。
(2)当容器中没有液体时,钩码所在的位置即为“密度天平”的“零刻度”,“零刻度”距离支点
O cm。
(3)若测量某种液体的密度时,钩码在距离支点右侧31cm处,液体的密度为 g/cm3。
(4)【拓展应用】若杠杆足够长,用此“密度天平”还可以测量固体的密度.先在容器中加满水,再将待测固体轻轻浸没在水中,溢出部分水后,调节钩码的位置,使杠杆水平平衡,测出钩码离支点O的距离为56cm;用量筒测出溢出水的体枳如图乙所示,则固体的密度为 kg/m3(已知ρ水=1.0g/cm3)。
参考答案
1.D
【解析】A.B点到O点的距离虽然是最远的,但是由于拉力的方向不一定,因此动力臂不一定是最长的,即有可能小于阻力臂,变成一个费力杠杆,故A错误;
B.C点向上用力,也能使杠杆平衡,故B错误;
C.当在B点用力时,如果力的方向与OB垂直向上,那么此时动力臂最长最省力,故C错误;
D.AO=OD,则动力臂等于阻力臂,如果两个物体的重力相等,那么动力×动力臂=阻力×阻力臂,因此杠杆能够平衡,故D正确。 故选D。
2.C
【解析】(1)甲杠杆:
浸没水中之前:G1L1=G2L2;
ρ物gV1×L1=ρ物gV2×L2;
则V1×L1=V2×L2;
浸没水中后左端力和力臂的乘积为:
(G1-F浮1)×L1=(ρ物gV1-ρ水gV1)×L1=(ρ物-ρ水)gV1×L1,
浸没水中后右端力和力臂的乘积为:
(G2-F浮2)×L2=(ρ物gV2-ρ水gV2)×L2=(ρ物-ρ水)gV2×L2,
所以浸没水中后,左右两端力和力臂的乘积相等,
故杠杆仍然平衡。
(2)乙杠杆:
浸没水中之前:G1L1=G2L2;
ρ1gV×L1=ρ2gV×L2,
浸没水中后左端力和力臂的乘积为:
(G1-F浮1)×L1=(ρ1gV-ρ水gV)×L1=ρ1gV×L1-ρ水gV×L1,
浸没水中后右端力和力臂的乘积为:
(G2-F浮2)×L2=(ρ2gV-ρ水gV)×L2=ρ2gV×L2-ρ水gV×L2,
因为L1<L2,
所以,左端力和力臂的乘积大于右端力和力臂的乘积, 故杠杆左端下沉。 故选C。
3.A
【解析】(1)G2在C点时,由杠杆平衡条件得:FA×OA=G2×OC;
即:FA×20cm=20N×10cm,
解得:FA=10N;
物体与地面的接触面积:S=5cm×5cm=25cm2=0.0025m2;
物体G1对地面的压力:F=pS=2×104Pa×0.0025cm2=50N,
地面对物体的支持力:F′=F=50N;
G1受竖直向下的重力G1、地面的支持力F′、绳子的拉力FA作用,
物体静止,处于平衡状态,由平衡条件得:G1=FA+F′=10N+50N=60N;
(2)当G1对地面的压力为0时,杠杆在A点的受到的拉力FA′=G1=60N,
设G2位于D点,由杠杆平衡条件得:FA′×OA=G2×OD;
即:60N×20cm=20N×OD,
解得:OD=60cm,
物体G2的路程:s=OD-OC=60cm-10cm=50cm,
物体G2的运动时间:。 故选A。
4.A
【解析】当把铝条a放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:;动力为铝条a的重力Ga,作用在它的中点处,动力臂为,
根据杠杆的平衡条件得到:①;
当把铝条b放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:;动力为铝条a的重力Ga,作用在它的中点处,动力臂为,
根据杠杆的平衡条件得到:②;
①÷②得到:
③;
因为铝条a和b横截面积相等,根据公式G=ρVg=ρShg可知,铝条的重力与长度成正比,
即:;
将其袋入③得到:;
因为La所以;
那么;
化简得到:;
整理得到:;
即:;
那么:。
如果支点O不动,因为Lb>La,所以肯定后有一部分在O点左侧。与原来相比可知,此时左边重力增大,为了维持平衡,必须减小阻力臂,增大动力臂,即支点向左移动,那么La故A正确,B错误;
若LbLa,故C、D错误。 故选A。
5.D
【解析】作图如下:
因为T1、T2的合力与电灯是一对平衡力,所以它的大小和方向保持不变,体现在平行四边形中就是对角线的位置和长度保持不变,又保持O与B点的位置不变,所以意味着沿着OB的这条边的方向也保持不变,所以它的对边的平行线位置也保持不变,这样当将悬挂点A向上移就意味着是沿着OB的对边向上移动,所构成的平行四边形的边长就是T1、T2的大小。由图可以看出悬挂点A向上移OA,OA'这条边是先变短后边长,所以T1先减小后增大;OB的长度是这条边是一直变短,所以T2一直减小,D说法正确。 故答案为:D
6.B
【解析】人从吊桥左端出发,在运动时间t后,杠杆受到物体的压力(阻力)等于人的重力,
动力臂为OA=L,杠杆受到物体的压力(阻力)F′=G,阻力臂为OB,OB=vt,
∵杠杆平衡,
∴F×OA=F′×OB=G×vt,
即:F×L=G×vt,
∴ ,
由此可知,当t=0时,F=0;当t增大时,F变大,是正比例关系;故选B。
7.A
【解析】①物体C向右运动,相当于AB向左运动,因此物体C对AB的摩擦力方向向右,故①正确;
②木块AB受到重力、支持力、摩擦力以及墙壁的支持力,故②错误;
③对面对C的支持力等于木板AB的压力和C的重力之和,与C的重力大小不同,肯定不是平衡力,故③错误;
④B为支点,AB的重力为阻力F2,阻力臂为AB的一半保持不变;C的支持力为动力,CB为动力臂;根据杠杆的平衡条件F1L1=F2L2可知,C向右运动,动力臂CB变小,那么动力肯定增大,即C对AB的支持力增大;根据相互作用力原理可知,AB对C的压力增大,因此C受到的摩擦力肯定增大,那么水平力F肯定增大。
上面说法正确的是①④。 故选A。
8.向下;30;省力
【解析】B点为支点,购物车的重力为阻力,阻力臂为0.3m;在A点施加动力,当以AB为动力臂时最长,此时动力最小,因此最小力的方向与AB垂直向下;
此时动力臂为:;
根据杠杆的平衡条件得到:100N×0.3m=F×1m;
解得:F=30N; 因为动力臂>阻力臂, 所以此时购物车可视为省力杠杆。
9.(1)30(2)1500(3)增大(4)均匀
【解析】(1)根据杠杆的平衡条件公式F1L1=F2L2得:G桶×OA=G钩码×L2;
120g×10cm=40g×L2,
解得:L2=30cm。
(2)根据题意可知,当钩码移动至最右端,该“密度天平”达到最大量程,
设OA为L1′,O点距最右端的距离为L2′,容器的质量为m1,钩码的质量为m2,容器中加满液体的质量为m,
由杠杆的平衡条件F1L1=F2L2得,(m1+m)gL1′=m2gL2′,
(m1+m)L1′=m2L2′;
(120g+m)×10cm=40g×60cm;
解得:m=120g;
则测量液体的最大密度为:。
(3)当钩码的质量适当增大时,则杠杆右侧的力增大,在力臂关系相同的情况下,左侧的液体重力也会增大,那么液体的密度会增大,即该“密度天平”的量程将增大。
(4)由杠杆的平衡条件F1L1=F2L2得:
(m1+m)gL1=m2gL2;
(m1+m)L1=m2L2;
(m1+ρV)L1=m2L2;
解得:;
上式子中,m2、V、L1都是常量,则液体的密度与L2为一次函数关系,
因此“密度天平”上的刻度是均匀的。
10.4;2:1:3
【解析】(1)根据公式m=ρV=ρSh可知,
三蜡烛的质量之比:ma:mb:mc=ρhSa:ρhSb:ρhSc=Sa:Sb:Sc=1:4:2;
设ma=M,则mb=4M,mc=2M,
根据杠杆的平衡条件得到:mag×L1+mbg×L2=mcg×L3,
Mg×4L2+4Mg×L2=2Mg×L3,
解得:L3=4L2;
(2)因为木条原来平衡,
所以:Mg×L1+4Mg×L2=2Mg×L3,
即L1+4L2=2L3,-----①
由题知,蜡烛在相等时间内燃烧的质量相同,则在相同的时间内三蜡烛减小的质量m相同,
要使木条平衡,两边减去的力和力臂的乘积相等,即mg×L1+mg×L2=mg×L3,
即L1+L2=L3,-------②
①-②得:
3L2=L3,----------③
即L2:L3=1:3,
由②得:
2L1+2L2=2L3,-------④
①-③得:
2L2=L1,-------------⑤
由③⑤得:
L1:L2:L3=2:1:3。
11.费力;
【解析】(1)根据图片可知,如果将人的重力看做动力,则动力臂为;绳子的拉力看做阻力,阻力臂为AB。此时动力臂小于阻力臂,为费力杠杆。
(2)根据图片可知,B点为支点,阻力为绳子上的拉力FA,
而动力F1=G人+G木板-FA=mg-FA;
根据杠杆的平衡条件F1L1=F2L2得到:(mg-FA)×=FA×AB; 则此人的拉力FA=。
12.(1)AD(2)32.5(3)小于
【解析】(1)推翻油桶时,可以将油桶看做一个杠杆,支点是D点,而油桶上到D的距离最大的点就是A点,所以所需最小力的力臂是AD;
(2)甲中油桶直立时,油桶重心的高度为:;
AD的长度为:;
那么油桶上升到最高点时重心高度为:;
因此小明至少需要对油桶做功:W=G△h=65kg×10N/kg×(0.65m-0.6m)=32.5J;
(3)甲和乙中,阻力都是油桶的重力G保持不变,最小力的力臂都等于油桶对角线的长度,也保持不变;乙图中的阻力臂为0.6m,甲图中的阻力臂为0.25m,那么重新竖起油桶时的阻力臂增大了,根据公式G×L2=F×L1可知,那么动力肯定也增大了,即F1<F2。
13.(1)100;15000(2)靠近
【解析】(1)将弟弟的肩膀看作支点,根据杠杆的平衡条件得到:G×L2=F姐×L1;
200N×L1=F姐×L1;
解得:F姐=100N;
弟弟对杆子的支持力为:F弟=G-F姐=200N-100N=100N。
弟弟对地面的压力为:F=G弟+F弟=50kg×10N/kg+100N=600N;
弟弟对地面的压强为:。
(2)快递的重力不变,要减小弟弟的压力,就要增大姐姐的压力。根据杠杆的平衡条件G×L2=F姐×L1可知,当G和L1不变时,增大F姐就要增大L2,即增大快递到弟弟肩膀的距离,将悬挂点O靠近姐姐的肩膀。
14.44;16
【解析】(1)当AB处于静止状态时,它向下受到重力G,向上受到支持力FA和FB,那么:G=FA+FB=6N+18N=24N;
(2)将B点看作支点,当A点在甲的小木块上时,
根据杠杆的平衡条件得到:6N×AB=G×L2;
当C点在甲的小木块上时,
根据杠杆的平衡条件得到:F甲×=G×L2;
两式联立计算得到:F甲=8N;
此时托盘秤乙的示数为:F乙=G-F甲=24N-8N=16N。
15.(1)减小。当α角增大时,F2力臂变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小。
(2)乙
【解析】(1)当α角增大时,F1将减小,理由:当α角增大时,F2力臂变小,阻力为箱子的重力不变。由于拉力F1的方向与脊柱夹角始终为12°,且OA距离不变,则O点到F1作用线的距离不变,即动力臂不变,根据杠杆平衡条件F1L1=F2L2可知,F1变小。
(2)比较甲、乙两种姿势可知,甲的支点比乙的支点高,在搬起物体的过程中,阻力臂减小的更慢,背部肌肉拉力作用的时间更长,因此会感觉更费力,所以乙图中的姿势比较正确。
16.水能完全浸没金属块但又没有水溢出;大于;
【解析】(2)由实验步骤可知,没有加入水之前是为了测量金属块的重力;而加入水后的读数是通过浮力来测量金属块的体积,从而计算金属块的密度,所以适量的水是指恰好把金属块完全浸没但又没有的水的体积;由于第二步有浮力的原因,则阻力减小,即F2要减小,所以F1>F2;
(3)由步骤一可知,,
∵OA:OB=1:3
∴G=3F1;
∴;
由步骤二可知,
∴F=3F2;
∴F浮=G-F=3(F1-F2);
∴;
∴;
17.(1)右(2)22(3)0.9(4)5000
【解析】【测量过程】
(1)杠杆左端下沉,说明杠杆左端重,右端轻,要使它在水平位置平衡,两端的螺母都要向杠杆的右端调节;
(2)根据杠杆平衡条件F1L1=F2L2得:110g×10cm=50g×L2,
解得:L2=22cm;
(3)设OA为L1′=10cm,O点距钩码的距离为L2′=31cm,
容器的质量为m1=110g,钩码的质量为m2=50g,容器中加满液体的质量为m,
由F1L1=F2L2得:(m1+m)gL1′=m2gL2′,
即(110g+m)×10cm=50g×31cm,
解得:m=45g,
液体的体积V=50mL=50cm3,
则液体的密度:;
(4)【拓展应用】由图可知,量筒中液体的凹液面的底部与30mL刻度线相平,
因为物体浸没在水中,所以待测固体的体积:V′=V溢水=30mL=30cm3,
固体放入容器后剩余水的体积:
V剩=V-V溢水=50mL-30mL=20mL=20cm3,
容器内剩余水的质量:m剩=ρ水V剩=1g/cm3×20cm3=20g,
由F1L1=F2L2得,(m1+m剩+m′)gL1″=m2gL2″,
即(110g+20g+m′)×10cm=50g×56cm,
解得m′=150g,
则此固体的密度:。
杠杆的应用
A.在B点用力使杠杆在图示位置平衡,一定是省力的
B.在C点用力不可能使杠杆在图示位置平衡
C.在B点用力使杠杆在图示位置平衡,沿竖直方向最省力
D.在D点悬挂一个与G完全相同的物体能使杠杆在图示位置平衡
2.小华在做实验时提出了如图所示两个模型,两杠杆均处于平衡状态,甲杠杆上平衡的是两个密度相同但体积不同的实心物体,乙杠杆上平衡的是两个体积相同但密度不同的实心物体(物体的密度都大于水)。如果将它们都浸没在水中,则两杠杆将( )
A.仍保持平衡 B.都失去平衡
C.甲仍保持平衡,乙失去平衡 D.甲失去平衡,乙仍保持平衡
3.如图所示,一轻质杠杆AB支在支架上,OA=20cm,G1为一边长为5cm的正方体,G2重为20N.当OC=10cm时,G1对地面的压强为2×104Pa。现用一水平拉力F使G2以2cm/s的速度向右匀速运动,则当G1对地面的压力为0时所经过的时间为 ( )
A.25s B.30s C.35s D.40s
4.现有一根形变不计、长为L的铁条AB和两根横截面积相同、长度分别为La、Lb的铝条a、b。将铝条a叠在铁条AB上,并使它们的右端对齐,然后把它们放置在三角形支架O上,AB水平平衡,此时OB的距离恰好为La,如图所示。取下铝条a后,将铝条b按上述操作方法使铁条AB再次水平平衡,此时OB的距离为Lx。下列判断正确的是( )
A.若La
C.若Lb
A.T1减小 B.T2增大 C.T1增大 D.T2减小
6.如图所示,用轻质材料制成的吊桥搭在河对岸.一个人从桥的左端匀速走到桥的右端,桥面始终是水平的,不计吊桥和绳的重力,人从吊桥左端出发时开始计时.则人在吊桥上行走过程中,吊桥右端所受地面支持力F与人行走时间t的关系图像是
A.B.C.D.
7.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中( )
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确 B.只有②③正确
C.只有①②正确 D.只有③④正确
8.小金推着购物车在超市购物,如右图所示,购物车和货物的总重为100N,A点离地面距离为0.8m,B、C点为车轮与地面的接触点,当购物车前轮遇到障碍物时,小金先后在A点对购物车施加了最小作用力。在使车的前轮越过障碍物时,施加的最小力的方向为 ,最小力的大小为 N;此时购物车可视为 杠杆(选“省力”“费力”“等臂”)。
9.如图装置为科技创新大赛时发明的可以直接测量液体密度的“密度天平”。其制作过程和原理如下:选择一根长1.2米的均匀杠杆,支点在其中点,调节两边螺母使杠杆在水平位置平衡,在左侧离中点10厘米的位置用细线固定一个质量为 120 克、容积为80毫升的容器,右侧用细线悬挂一质量为40克的钩码(细线的质量忽略不计)。测量时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位置直接读出液体的密度。
(1)该“密度天平”的“零刻度”应标在右端离支点 厘米处;
(2)该“密度天平”的最大刻度值为 kg/m3;
(3)若将钩码的质量适当增大,该“密度天平”的量程将 (选填“增大”、“减小”或“不变”) ;(4)该“密度天平”的刻度是 的(“均匀”、“不均匀”)
10.如图所示,一均匀木条可绕转轴O自由转动,现有材料相同,长度相同,横截面积之比Sa:Sb:Sc=1:4:2的三支蜡烛a、b、c,垂直立于木条上,木条恰好处于平衡。三支蜡烛离转轴的距离分别为L1、L2和L3,若L1=4L2,则L3= L2。若同时点燃蜡烛蜡烛在燃烧过程中,要使杠杆保持平衡,则L1:L2:L3= (蜡烛在相等时间内燃烧的质量相同)。
11.如图所示,质量为m的人站在质量为的均匀木板AB的中点,木板可以绕B端转动,2若以人的重力为动力,这属于 (选填“省力”或“费力”)杠杆。要使木板处于水平状态不动,此人拉力的大小为 。(摩擦忽略不计)
12.如图为油厂的油桶,空桶质量为65Kg,油桶高为1.2m,底部直径为0.5m,据此回答。
(1)某次装卸中,小明需要将直立的空油桶(如图甲)沿D点推翻,则甲图上推翻空油桶所需的最小力F1的力臂是 。(选填“CD”、“BD”或“AD”)
(2)在推翻油桶过程中,小明至少需要对油桶做功 焦。
(3)若将翻倒的空油桶(如图乙)重新竖起所用的最小力为F2,那么,F1 F2(选填“大于”、“等于”或“小于”)。
13.姐姐拿不动一大箱快递,喊弟弟一起用一根杆子把快递抬回家。姐姐和弟弟身高相仿,两人体重均约为50kg,双脚与地面接触面积均约为400cm2,肩膀对杆子作用点分别在杆子的两个端点,杆子重力忽略不计。快递箱总重为200N,悬挂点O恰在轻杆中点,问:
(1)静止不动时,姐姐肩膀受到的压力约为 N,弟弟对地面的压强约为 Pa
(2)走了一段路后,弟弟喊肩膀痛,为了减轻弟弟的压力,姐姐应把悬挂点O点 (选填“靠近”或“远离”或“不变”)自己的肩膀。
14.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上。木条AB质量分布不均匀,A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。托盘秤甲和乙的中心各固定有一个大小和质量不计的小木块,A端放在托盘秤甲的小木块上,B端放在托盘秤乙的小木块上,甲的示数是6N,乙的示数是18N。物体AB的重力为 N;若移动托盘秤甲,让C点放在托盘秤甲的小木块上,则托盘秤乙的示数是 N。
15.我们常见的从地面上搬起重物的做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?我们把脊柱简化为杠杆建立模型如图丙所示,脊柱可绕骶骨轴O转动,腰背肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论。
(1)当α角增大时,F1如何变化?并说明理由。
(2)比较甲、乙两种姿势所对应丙图中的两种状态,分析可得, (选填“甲”或“乙”)图中的姿势比较正确。
16.某同学要测一个金属块的密度,他手中的测量工具只有一只量程较小的弹簧测力计,当他用此弹簧测力计测量该金属块的重力时,发现已超过弹簧测力计的最大量程,于是他设计了如图所示的装置去测量。图中OA:OB=1:3。他实验的步骤如下:
⑴用细绳把金属块悬挂于A点,用弹簧测力计在B点作用一个竖直向上的力,使杠杆OAB在水平位置静止,金属块静止在空中,读出弹簧测力计此时的读数F1;
⑵向容器中加适量的水,“适量”指的是 ,待杆在水平位置重新平衡后,再读出弹簧测力计此时的读数F2,则F1 F2(选填“大于”、“等于”、“小于”);
⑶若杠杆OAB质量不计,则被测金属块密度的表达式:ρ= 。(水的密度表示为ρ水)
17.某同学制作了直接测量液体密度的“密度天平”.其制作过程和原理如下:如图甲所示,选择一个长杠杆,调节两边螺母使杠杆在水平位罝平衡;在左侧离支点10cm的位罝A用细线固定一个质量为110g、容积为50mL的容器.右侧用细线悬挂一质量为50g的钩码(细线的质量忽略不计)。
【测量过程】将下对实验空白处补充完整:
(1)调节杠杆平衡时,发现杠杆左端下沉,需将平衡螺母向 端调节(填“左”或“右”);测量液体时往容器中加满待测液体,移动钩码使杠杆在水平位置平衡,在钩码悬挂位罝直接读出液体密度。
(2)当容器中没有液体时,钩码所在的位置即为“密度天平”的“零刻度”,“零刻度”距离支点
O cm。
(3)若测量某种液体的密度时,钩码在距离支点右侧31cm处,液体的密度为 g/cm3。
(4)【拓展应用】若杠杆足够长,用此“密度天平”还可以测量固体的密度.先在容器中加满水,再将待测固体轻轻浸没在水中,溢出部分水后,调节钩码的位置,使杠杆水平平衡,测出钩码离支点O的距离为56cm;用量筒测出溢出水的体枳如图乙所示,则固体的密度为 kg/m3(已知ρ水=1.0g/cm3)。
参考答案
1.D
【解析】A.B点到O点的距离虽然是最远的,但是由于拉力的方向不一定,因此动力臂不一定是最长的,即有可能小于阻力臂,变成一个费力杠杆,故A错误;
B.C点向上用力,也能使杠杆平衡,故B错误;
C.当在B点用力时,如果力的方向与OB垂直向上,那么此时动力臂最长最省力,故C错误;
D.AO=OD,则动力臂等于阻力臂,如果两个物体的重力相等,那么动力×动力臂=阻力×阻力臂,因此杠杆能够平衡,故D正确。 故选D。
2.C
【解析】(1)甲杠杆:
浸没水中之前:G1L1=G2L2;
ρ物gV1×L1=ρ物gV2×L2;
则V1×L1=V2×L2;
浸没水中后左端力和力臂的乘积为:
(G1-F浮1)×L1=(ρ物gV1-ρ水gV1)×L1=(ρ物-ρ水)gV1×L1,
浸没水中后右端力和力臂的乘积为:
(G2-F浮2)×L2=(ρ物gV2-ρ水gV2)×L2=(ρ物-ρ水)gV2×L2,
所以浸没水中后,左右两端力和力臂的乘积相等,
故杠杆仍然平衡。
(2)乙杠杆:
浸没水中之前:G1L1=G2L2;
ρ1gV×L1=ρ2gV×L2,
浸没水中后左端力和力臂的乘积为:
(G1-F浮1)×L1=(ρ1gV-ρ水gV)×L1=ρ1gV×L1-ρ水gV×L1,
浸没水中后右端力和力臂的乘积为:
(G2-F浮2)×L2=(ρ2gV-ρ水gV)×L2=ρ2gV×L2-ρ水gV×L2,
因为L1<L2,
所以,左端力和力臂的乘积大于右端力和力臂的乘积, 故杠杆左端下沉。 故选C。
3.A
【解析】(1)G2在C点时,由杠杆平衡条件得:FA×OA=G2×OC;
即:FA×20cm=20N×10cm,
解得:FA=10N;
物体与地面的接触面积:S=5cm×5cm=25cm2=0.0025m2;
物体G1对地面的压力:F=pS=2×104Pa×0.0025cm2=50N,
地面对物体的支持力:F′=F=50N;
G1受竖直向下的重力G1、地面的支持力F′、绳子的拉力FA作用,
物体静止,处于平衡状态,由平衡条件得:G1=FA+F′=10N+50N=60N;
(2)当G1对地面的压力为0时,杠杆在A点的受到的拉力FA′=G1=60N,
设G2位于D点,由杠杆平衡条件得:FA′×OA=G2×OD;
即:60N×20cm=20N×OD,
解得:OD=60cm,
物体G2的路程:s=OD-OC=60cm-10cm=50cm,
物体G2的运动时间:。 故选A。
4.A
【解析】当把铝条a放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:;动力为铝条a的重力Ga,作用在它的中点处,动力臂为,
根据杠杆的平衡条件得到:①;
当把铝条b放在铁条上时,铁条的重力G铁为阻力,作用在中点,那么阻力臂为:;动力为铝条a的重力Ga,作用在它的中点处,动力臂为,
根据杠杆的平衡条件得到:②;
①÷②得到:
③;
因为铝条a和b横截面积相等,根据公式G=ρVg=ρShg可知,铝条的重力与长度成正比,
即:;
将其袋入③得到:;
因为La
那么;
化简得到:;
整理得到:;
即:;
那么:。
如果支点O不动,因为Lb>La,所以肯定后有一部分在O点左侧。与原来相比可知,此时左边重力增大,为了维持平衡,必须减小阻力臂,增大动力臂,即支点向左移动,那么La
若Lb
5.D
【解析】作图如下:
因为T1、T2的合力与电灯是一对平衡力,所以它的大小和方向保持不变,体现在平行四边形中就是对角线的位置和长度保持不变,又保持O与B点的位置不变,所以意味着沿着OB的这条边的方向也保持不变,所以它的对边的平行线位置也保持不变,这样当将悬挂点A向上移就意味着是沿着OB的对边向上移动,所构成的平行四边形的边长就是T1、T2的大小。由图可以看出悬挂点A向上移OA,OA'这条边是先变短后边长,所以T1先减小后增大;OB的长度是这条边是一直变短,所以T2一直减小,D说法正确。 故答案为:D
6.B
【解析】人从吊桥左端出发,在运动时间t后,杠杆受到物体的压力(阻力)等于人的重力,
动力臂为OA=L,杠杆受到物体的压力(阻力)F′=G,阻力臂为OB,OB=vt,
∵杠杆平衡,
∴F×OA=F′×OB=G×vt,
即:F×L=G×vt,
∴ ,
由此可知,当t=0时,F=0;当t增大时,F变大,是正比例关系;故选B。
7.A
【解析】①物体C向右运动,相当于AB向左运动,因此物体C对AB的摩擦力方向向右,故①正确;
②木块AB受到重力、支持力、摩擦力以及墙壁的支持力,故②错误;
③对面对C的支持力等于木板AB的压力和C的重力之和,与C的重力大小不同,肯定不是平衡力,故③错误;
④B为支点,AB的重力为阻力F2,阻力臂为AB的一半保持不变;C的支持力为动力,CB为动力臂;根据杠杆的平衡条件F1L1=F2L2可知,C向右运动,动力臂CB变小,那么动力肯定增大,即C对AB的支持力增大;根据相互作用力原理可知,AB对C的压力增大,因此C受到的摩擦力肯定增大,那么水平力F肯定增大。
上面说法正确的是①④。 故选A。
8.向下;30;省力
【解析】B点为支点,购物车的重力为阻力,阻力臂为0.3m;在A点施加动力,当以AB为动力臂时最长,此时动力最小,因此最小力的方向与AB垂直向下;
此时动力臂为:;
根据杠杆的平衡条件得到:100N×0.3m=F×1m;
解得:F=30N; 因为动力臂>阻力臂, 所以此时购物车可视为省力杠杆。
9.(1)30(2)1500(3)增大(4)均匀
【解析】(1)根据杠杆的平衡条件公式F1L1=F2L2得:G桶×OA=G钩码×L2;
120g×10cm=40g×L2,
解得:L2=30cm。
(2)根据题意可知,当钩码移动至最右端,该“密度天平”达到最大量程,
设OA为L1′,O点距最右端的距离为L2′,容器的质量为m1,钩码的质量为m2,容器中加满液体的质量为m,
由杠杆的平衡条件F1L1=F2L2得,(m1+m)gL1′=m2gL2′,
(m1+m)L1′=m2L2′;
(120g+m)×10cm=40g×60cm;
解得:m=120g;
则测量液体的最大密度为:。
(3)当钩码的质量适当增大时,则杠杆右侧的力增大,在力臂关系相同的情况下,左侧的液体重力也会增大,那么液体的密度会增大,即该“密度天平”的量程将增大。
(4)由杠杆的平衡条件F1L1=F2L2得:
(m1+m)gL1=m2gL2;
(m1+m)L1=m2L2;
(m1+ρV)L1=m2L2;
解得:;
上式子中,m2、V、L1都是常量,则液体的密度与L2为一次函数关系,
因此“密度天平”上的刻度是均匀的。
10.4;2:1:3
【解析】(1)根据公式m=ρV=ρSh可知,
三蜡烛的质量之比:ma:mb:mc=ρhSa:ρhSb:ρhSc=Sa:Sb:Sc=1:4:2;
设ma=M,则mb=4M,mc=2M,
根据杠杆的平衡条件得到:mag×L1+mbg×L2=mcg×L3,
Mg×4L2+4Mg×L2=2Mg×L3,
解得:L3=4L2;
(2)因为木条原来平衡,
所以:Mg×L1+4Mg×L2=2Mg×L3,
即L1+4L2=2L3,-----①
由题知,蜡烛在相等时间内燃烧的质量相同,则在相同的时间内三蜡烛减小的质量m相同,
要使木条平衡,两边减去的力和力臂的乘积相等,即mg×L1+mg×L2=mg×L3,
即L1+L2=L3,-------②
①-②得:
3L2=L3,----------③
即L2:L3=1:3,
由②得:
2L1+2L2=2L3,-------④
①-③得:
2L2=L1,-------------⑤
由③⑤得:
L1:L2:L3=2:1:3。
11.费力;
【解析】(1)根据图片可知,如果将人的重力看做动力,则动力臂为;绳子的拉力看做阻力,阻力臂为AB。此时动力臂小于阻力臂,为费力杠杆。
(2)根据图片可知,B点为支点,阻力为绳子上的拉力FA,
而动力F1=G人+G木板-FA=mg-FA;
根据杠杆的平衡条件F1L1=F2L2得到:(mg-FA)×=FA×AB; 则此人的拉力FA=。
12.(1)AD(2)32.5(3)小于
【解析】(1)推翻油桶时,可以将油桶看做一个杠杆,支点是D点,而油桶上到D的距离最大的点就是A点,所以所需最小力的力臂是AD;
(2)甲中油桶直立时,油桶重心的高度为:;
AD的长度为:;
那么油桶上升到最高点时重心高度为:;
因此小明至少需要对油桶做功:W=G△h=65kg×10N/kg×(0.65m-0.6m)=32.5J;
(3)甲和乙中,阻力都是油桶的重力G保持不变,最小力的力臂都等于油桶对角线的长度,也保持不变;乙图中的阻力臂为0.6m,甲图中的阻力臂为0.25m,那么重新竖起油桶时的阻力臂增大了,根据公式G×L2=F×L1可知,那么动力肯定也增大了,即F1<F2。
13.(1)100;15000(2)靠近
【解析】(1)将弟弟的肩膀看作支点,根据杠杆的平衡条件得到:G×L2=F姐×L1;
200N×L1=F姐×L1;
解得:F姐=100N;
弟弟对杆子的支持力为:F弟=G-F姐=200N-100N=100N。
弟弟对地面的压力为:F=G弟+F弟=50kg×10N/kg+100N=600N;
弟弟对地面的压强为:。
(2)快递的重力不变,要减小弟弟的压力,就要增大姐姐的压力。根据杠杆的平衡条件G×L2=F姐×L1可知,当G和L1不变时,增大F姐就要增大L2,即增大快递到弟弟肩膀的距离,将悬挂点O靠近姐姐的肩膀。
14.44;16
【解析】(1)当AB处于静止状态时,它向下受到重力G,向上受到支持力FA和FB,那么:G=FA+FB=6N+18N=24N;
(2)将B点看作支点,当A点在甲的小木块上时,
根据杠杆的平衡条件得到:6N×AB=G×L2;
当C点在甲的小木块上时,
根据杠杆的平衡条件得到:F甲×=G×L2;
两式联立计算得到:F甲=8N;
此时托盘秤乙的示数为:F乙=G-F甲=24N-8N=16N。
15.(1)减小。当α角增大时,F2力臂变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小。
(2)乙
【解析】(1)当α角增大时,F1将减小,理由:当α角增大时,F2力臂变小,阻力为箱子的重力不变。由于拉力F1的方向与脊柱夹角始终为12°,且OA距离不变,则O点到F1作用线的距离不变,即动力臂不变,根据杠杆平衡条件F1L1=F2L2可知,F1变小。
(2)比较甲、乙两种姿势可知,甲的支点比乙的支点高,在搬起物体的过程中,阻力臂减小的更慢,背部肌肉拉力作用的时间更长,因此会感觉更费力,所以乙图中的姿势比较正确。
16.水能完全浸没金属块但又没有水溢出;大于;
【解析】(2)由实验步骤可知,没有加入水之前是为了测量金属块的重力;而加入水后的读数是通过浮力来测量金属块的体积,从而计算金属块的密度,所以适量的水是指恰好把金属块完全浸没但又没有的水的体积;由于第二步有浮力的原因,则阻力减小,即F2要减小,所以F1>F2;
(3)由步骤一可知,,
∵OA:OB=1:3
∴G=3F1;
∴;
由步骤二可知,
∴F=3F2;
∴F浮=G-F=3(F1-F2);
∴;
∴;
17.(1)右(2)22(3)0.9(4)5000
【解析】【测量过程】
(1)杠杆左端下沉,说明杠杆左端重,右端轻,要使它在水平位置平衡,两端的螺母都要向杠杆的右端调节;
(2)根据杠杆平衡条件F1L1=F2L2得:110g×10cm=50g×L2,
解得:L2=22cm;
(3)设OA为L1′=10cm,O点距钩码的距离为L2′=31cm,
容器的质量为m1=110g,钩码的质量为m2=50g,容器中加满液体的质量为m,
由F1L1=F2L2得:(m1+m)gL1′=m2gL2′,
即(110g+m)×10cm=50g×31cm,
解得:m=45g,
液体的体积V=50mL=50cm3,
则液体的密度:;
(4)【拓展应用】由图可知,量筒中液体的凹液面的底部与30mL刻度线相平,
因为物体浸没在水中,所以待测固体的体积:V′=V溢水=30mL=30cm3,
固体放入容器后剩余水的体积:
V剩=V-V溢水=50mL-30mL=20mL=20cm3,
容器内剩余水的质量:m剩=ρ水V剩=1g/cm3×20cm3=20g,
由F1L1=F2L2得,(m1+m剩+m′)gL1″=m2gL2″,
即(110g+20g+m′)×10cm=50g×56cm,
解得m′=150g,
则此固体的密度:。
杠杆的应用
同课章节目录
