第4章 《基本平面图形》复习教案

课题：第四章复习
【课标与教材分析】：
课标要求：（1）会比较线段的长短，理解线段的和、差，以及线段中点的意义。
（2）掌握基本事实：两点确定一条直线。
（3）掌握基本事实：两点之间线段最短。
（4）理解两点间距离的意义，能度量两点间的距离。
（5）理解角的概念，能比较角的大小。
（6）认识度、分、秒，会对度、分、秒进行简单的换算，并会计算角的和、差。
教材分析：本章以线段，直线，射线，角等简 ( http: / / www.21cnjy.com )单的图形为主要研究对象，使学生在活动中体会这些平面图形的性质及其位置关系，丰富了学生的数学活动经历。它是学习了第一章《丰富的图形世界》以后学生再次接触几何图形，为以后学习几何图形打下了基础。本节复习课可以使学生对本章所研究的基本元素和基本关系有进一步的认识。
【学情分析】：
学生已经知道的：本节课是第四章的复习课。学 ( http: / / www.21cnjy.com )生在本章的各小节中学习了线段，射线，直线和角的基本概念，学习了如何比较线段的大小，如何比较角的大小，对于一些基本的几何图形有了初步的认识。
学生能自己解决的：学生能够区分线段射线和直 ( http: / / www.21cnjy.com )线，知道它们之间的区别和联系，能用不同方法比较线段长短和角的大小。对于线段中点和角平分线会简单应用。
需要教师指导解决的：关于线段的中点和角平分线的应用还需要教师的进一步指导。
【教学目标分析】：　
（一）教学目标：
1、知识技能：让学生在自我回顾及小组交流活动中，构建本章的基本知识框架，从而对本章的基本知识有更进一步的认识；
2、数学思考：在数学活动中积累活动经验，发展有条理的思考与表达；
3、问题解决：通过本节课的学习，进一步增强学生对所学知识的应用意识；
4、情感目标：培养学生自主学习，主动参与，主动交流合作的意识和能力。
（二）教学重点：培养学生自主学习，主动参与，主动交流合作的意识和能力。
（三）教学难点：线段的中点和角平分线知识的应用。
（四）创新支点设计：
【教学评价】：充分发挥学生 ( http: / / www.21cnjy.com )的主体作用，教师的主导作用，采用学生自评、生生互评与教师评价相结合的方式，通过课堂观察学生的学习表现、练习题的解答，及时对学生数学学习的过程进行评价，课后通过作业反馈评价
【教学方法与媒体】：多媒体课件，自主探索与合作交流相结合。
在课堂教学中，根据教学重难点对本章知识建构，通过学生的自学，小组讨论，充分发挥学生的主体作用及教师的主导作用。
【教学过程】：
第四章复习回顾
学习过程：
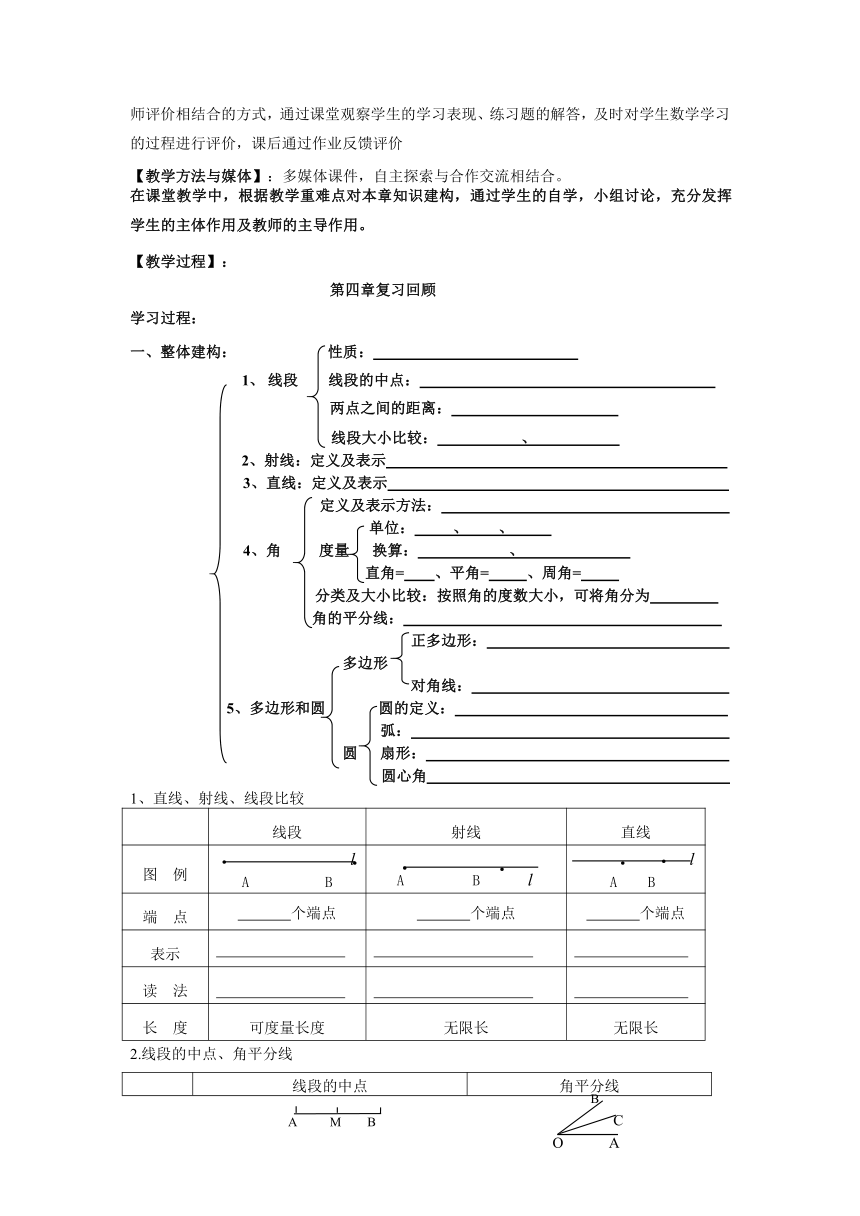
一、整体建构： 性质：
线段 线段的中点：
两点之间的距离：
线段大小比较： 、
2、射线：定义及表示
3、直线：定义及表示
定义及表示方法：
单位： 、 、
4、角 度量 换算： 、
直角= 、平角= 、周角=
分类及大小比较：按照角的度数大小，可将角分为
角的平分线：
正多边形：
多边形
对角线：
5、多边形和圆 圆的定义：
弧：
圆 扇形：
圆心角
1、直线、射线、线段比较
线段 射线 直线
图 例 A B A B A B
端 点 个端点 个端点 个端点
表示
读 法
长 度 可度量长度 无限长 无限长
2.线段的中点、角平分线
线段的中点 角平分线
示意图
定义 点M把线段AB分成 的两条线段AM和BM,点M叫做线段AB的中点. 从一个角的顶点引出的一条射线,把这个角分成 的角,这条射线叫做这个角的平分线.
符号 AM= = , 或AB= = . = =∠AOB,或∠AOB= = .
二、 典型考题
题型1直线、射线、线段
1、下列说法：①直线AB与 ( http: / / www.21cnjy.com )直线BA是同一条直线；②射线AB与射线BA是同一条射线；③线段AB与线段BA是同一条线段；④直线、射线和线段上有无数多个点。其中错误的是
2、过平面内一点，能画 直线，过平面内两点能画 直线；
3、在直线上取三点A，B，C，且AB=6，BC=4，则AC=__________
4、栽树时，只要确定（ ）个树坑的位置，就可以确定同一行树坑所在的位置，其原理是
5、已知线段AB=8cm，在直线AB上画线段BC ，使它等于３cm ，则线段AC＝ （　　）
A.　１１cm B. ５cm C.１１cm或５cm D.８cm或１１cm
6、如果线段AB=５cm，BC＝４cm，则A、C两点间的距离是 （　　）
A.　１cm B. ９cm C.１cm或９cm D.以上答案都不对
如图点C是线段AB上一点，点M是AC的中点，点N是BC的中点。
若AM=2，BC=6，求MN的长度；
若AB=20，求MN的长度。
题型2：角
1、小明利用星期天搞社会调查活动，早晨8：00出发，中午12：35
到家，则出发时和到家时，时针和分针的夹角分别为________和________.
2、0.75°= ′= ″;4.62°= ° ′ ″
45°23′45″= °
3、如果一个角的补角是150°,那么这个角的余角是 ( )
A.30° B.60° C.90° D.120°
4、不能用一副三角板拼出的角是 ( )
A.120° B.75° C.105° D.100°
5、如图,在下列横线上填上适当的角.
∠AOC = + ;
∠AOD -∠BOD = ;
∠BOC = -∠COD;
∠BOC =∠AOC + - .
6、如图的度数为（ ）
7、如图，∠AOE是一个平角，OB平分∠AOC，OD平分∠COE，则∠BOD＝_____.
8、平面内，有两个角∠AOB=50°，∠AOC=20°，OA为两角的公共边，则∠BOC 为（ ）
A． 30° B. 70° C. 30°或70° D. 无
9、如图和都是直角
猜想与图中哪个角相等；
若=30 ，求的度数。
题型3、多边形和圆
1、如图，圆的四条半径分别是OA，OB，OC，OD，其中点O，A，B在
同一条直线上，∠AOD＝90°，∠AOC＝3∠BOC，那么圆被四条半径
分成的四个扇形的面积的比是（ ）
(A)1∶2∶2∶3 (B) 3∶2∶2∶3 (C) 4∶2∶2∶3 (D) 1∶2∶2∶1
2、n边形有 个顶点 个内角 条对角线。
3、半径为2的圆中，扇形AOB的圆心角为120°，计算扇形的面积.
三、整体建构
四、当堂测试
1、如图，下列各式中错误的是 （　　）
A. AB=AD+DB B. CB=AB-AC C. CB-DB=CD D. CB-DB=AC
2、已知AD=6cm，BD=2cm，C是线段AD的中点，则BC= cm.
3、已知线段AB = 10.8cm，AB的中点为C，AB的三等分点为D，则C、D两点之间的距离为 .
4、2时15分，钟表中时针与分针的夹角为 （ ）
A.30° B.45° C.22.5° D.15°
5、（1）21.5°= 分= 秒 （2）360″= ′= ″
6、如图2，∠AOB=∠AOC, ∠BOC=86°,则∠AOB= .
7、如图3，∠1=∠2=∠3=20°,则∠AOB= ， ∠AOC= ∠AOD,
∠BOD= ∠2，∠AOC= ∠1.
五、课后达标
A组
1．下列图中角的表示方法正确的个数有（ ）
( http: / / www.21cnjy.com )
A．1个 B．2个 C．3个 D．4个
2. 如图，以O为端点的射线共有多少条 ( )
A.1 B.2 C.3 D.4
3.在同一直线上有若干个 ( http: / / www.21cnjy.com )点，若构成的射线共有20条，则构成的线段共有 （ ）A.10条 B.20条 C.45条 D.90条
4. 两根木条，一根长60 cm，一根 ( http: / / www.21cnjy.com )长100 cm，将它们的一个端点重合，放在同一条直线上，此时两根木条的中点间的距离是 cm.
5．下列说法正确的是 （ ）
A.两条射线就是一个周角 B.一条射线就是一个周角 C.角的两边越长，角就越大
D.一条射线绕着端点从起始位置旋转到终止位置所形成的图形叫做角
B组
6. 如图,直线AB、CD相交于点O，作∠DOE ＝∠BOD, OF平分∠AOE，若∠AOC＝28°,则∠EOF= 度.
7.如图BOOC，OD是的平分线，。
求度数
8.已知：线段a、b（a>b），
求作：线段AB，使AB＝2a-b。
六、课后反思
【板书设计】：
第四章复习
1、线段、射线、直线 4、多边形和圆
2、线段的中点和角平分线 5、例题分析
3、角
·
·
·
·
·
·
A M B
B
C
O A
M
N
B
C
A
C
B
O
A
D
D
C
B
A
O
D
C
A
O