4.3.1等比数列的概念 第2课时 教学设计
文档属性
| 名称 | 4.3.1等比数列的概念 第2课时 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 607.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 17:01:12 | ||
图片预览


文档简介
第四章 数列
《4.3.1等比数列的概念》教学设计
第2课时
1.能够运用等比数列的知识解决简单的实际问题.
2.能够运用等比数列的性质解决有关问题.
教学重点:运用等比数列解决简单的实际问题
教学难点:等比数列的综合运用.
PPT课件.
【新课导入】
问题1:阅读课本第31~33页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
师生活动:学生带着问题阅读课本,并在本节课中回答相应问题.
预设的答案:(1)本节课主要学习等比数列的概念及等比数列的通项公式的应用.(2)在已学习了等比数列的概念及等比数列的通项公式的基础上,让学生学会运用概念和公式解决相关问题,学会观察、归纳、反思,进一步培养学生灵活运用公式的能力以及分析问题和解决问题的能力.发展学生逻辑推理、直观想象、数学运算和数学建模的的核心素养.
设计意图:通过阅读读本,让学生明晰本阶段的学习目标,初步搭建学习内容的框架.
问题2:上节课我们学习了哪些知识?
师生活动:学生回顾并回答,教师完善.
设计意图:通过复习上节课内容,加强记忆,温故而知新.
问题3:类比等差数列,等比数列是不是也有下标和性质呢?
师生活动:学生思考,教师总结.
设计意图:通过该问题,引入新课.
【探究新知】
知识点1等比数列的性质
等比数列{an }中,若m,n,r,s∈N+,且m+n=r+s,则am·an=ar·as.
证明:设公比为q,因为,则,,,
所以,,
所以am·an=ar·as.
特别地,若2p=m+n,则ap2=aman.
设计意图:让学生会用等比数列的通项公式证明等比数列的下标和性质.
【练一练】递增等比数列{an }中,a3 +a6 =9,a4 a5=8,则数列{an }的公比为____.
预设的答案:由等比数列的性质知a4 a5= a3 a6=8,又a3 +a6 =9,且是递增数列,所以a3=1,a6=8,所以公比为2.
【巩固练习】
例1 用 10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
师生活动:让学生认真读题、审题,说出大致解题思路,教师完善.
预设的答案:(1)设这笔钱存n个月以后的本利和组成一个数列{an },
则{an }是等比数列,
首项a1=104 (1+0.400%),公比 q=1+0.400%,
所以a12=a1 q11 =104 (1+0.400%)12≈10 490.7.
所以,12个月后的利息为10 490.7-104≈491(元).
(2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列{an },则{bn }也是一个等比数列,
首项,公比为1+r,
于是.
因此,以季度复利计息,存4个季度后的利息为元.
解不等式,得.
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
设计意图:通过运用等比数列模型解决实际问题,发展学生逻辑推理、数学抽象和数学建模的核心素养.增强学生的数学应用意识.
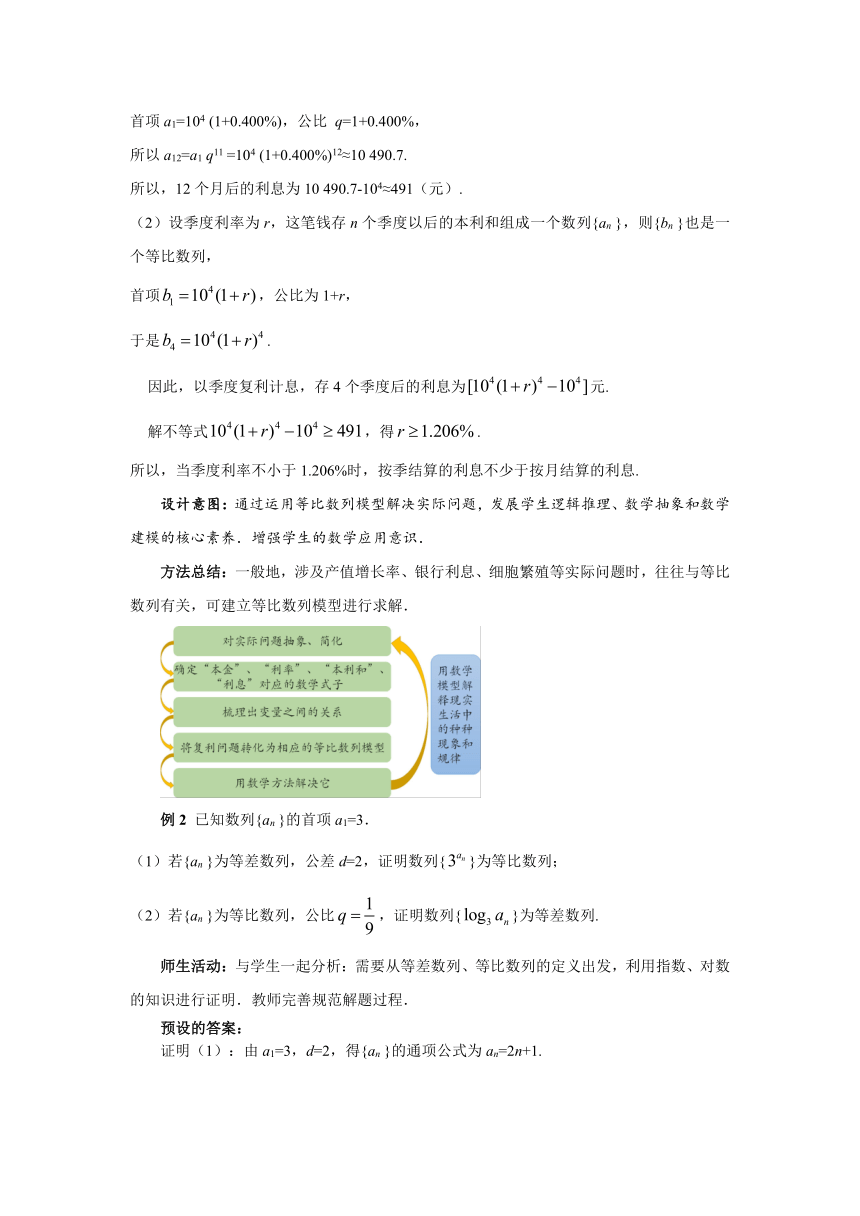
方法总结:一般地,涉及产值增长率、银行利息、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解.
例2 已知数列{an }的首项a1=3.
(1)若{an }为等差数列,公差d=2,证明数列{}为等比数列;
(2)若{an }为等比数列,公比,证明数列{}为等差数列.
师生活动:与学生一起分析:需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明.教师完善规范解题过程.
预设的答案:
证明(1):由a1=3,d=2,得{an }的通项公式为an=2n+1.
设bn=3an )=32n+1,则 :,
又 b1=33=27,
所以,{}是以 27为首项,9为公比的等比数列.
证明(2):由a1=3, ,得,
两边取以3为底的对数,得.
所以.又 ,
所以,{}是首项为1,公差为-2的等差数列.
设计意图:通过该典型例题,加深对等差与等比数列概念的理解,体会等差与等比数列的内在联系.提升学生逻辑推理、直观想象、数学抽象和数学运算的核心素养.
结论:1. 若数列{an }是等差数列,则数列{}是等比数列;
2.若数列{an }是各项均为正的等比数列,则数列{}是等差数列.
例3 某工厂去年12月试产1050个高新电子产品,产品合格率为.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高,产品合格率比前一个月增加,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
师生活动:与学生一起分析:设从今年1月起各月的产量及合格率分别构成数列{an},{bn },则各月不合格品的数量构成数列{an bn },由题意可知,数列{an }是等比数列,数列{bn}是等差数列,由于数列{an bn }既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.教师完善解题过程.
预设的答案:(1)设从今年1月起,各月的产量及不合格率分别构成数列{an},{bn}由题意,知
an=10501.05n-1,bn=1-[90%+0.4%(n-1)]=0.104-0.004n, 其中n=1,2,…,24,
则从今年1月起,各月不合格产品的数量是an bn=10501.05n-1(0.104-0.004n),
由计算工具计算(精确到0.1),并列表
观察发现,数列{an bn }先递增,在第6项以后递减,所以只要设法证明当n≥6时,{an bn }递减,且a13 b13<100即可.
由,
得n>5.
所以,当n≥6时,{an bn }递减,又a13 b13≈98<100,
所以当13≤n≤24时, an bn ≤a13 b13<100
所以,生产该产品一年后,月不合格的数量能控制在100个以内.
设计意图:通过该题,加深学生对等比数列的综合运用能力.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
方法总结:通常利用相邻项的大小比较得出数列的单调性.而数列两项大小比较可用作差法也可用作商法.
练习:教科书P34 练习2 、4
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
【课堂总结】
1.板书设计:
4. 3.1等比数列的概念(2)
一、探索新知 二、初步应用
1.等比数列的性质 例1
知识讲解1: 例2
例3
2.总结概括:
师生活动:学生总结,老师适当补充.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
3.课堂作业:教科书P34 练习1 、3 、5
【目标检测设计】
1.在流行病学中,基本传染数是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数. 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假定某种传染病的基本传染数,那么感染人数由1个初始感染者增加到2000人大约需要的传染轮数为( )
注:初始感染者传染个人为第一轮传染,这个人再传染个人为第二轮感染.
A.5 B.6 C.7 D.8
设计意图:让学生进一步巩固等比数列的定义及通项公式的实际应用.
2.已知等比数列的各项均为正数,且,则_____.
设计意图:让学生进一步巩固等比数列的性质.
3. 2017年,某县甲、乙两个林场森林木材的存量分别为16a和25a,
甲林场木材存量每年比上一年递增25%,而乙林场木材存量每年比上一年递减20%.
(1)哪一年两林场木材的总存量相等?
(2)两林场木材的总量到2021年能否翻一番?
设计意图:让学生进一步巩固等比数列通项公式的实际应用.
参考答案:1.B 2.10
3.解:(1)由题意可得
16a(1+25%)n-1=25a(1-20%)n-1,
解得n=2,
故到2019年两林场木材的总存量相等.
(2)令n=5,则,
故到2021年不能翻一番.
《4.3.1等比数列的概念》教学设计
第2课时
1.能够运用等比数列的知识解决简单的实际问题.
2.能够运用等比数列的性质解决有关问题.
教学重点:运用等比数列解决简单的实际问题
教学难点:等比数列的综合运用.
PPT课件.
【新课导入】
问题1:阅读课本第31~33页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
师生活动:学生带着问题阅读课本,并在本节课中回答相应问题.
预设的答案:(1)本节课主要学习等比数列的概念及等比数列的通项公式的应用.(2)在已学习了等比数列的概念及等比数列的通项公式的基础上,让学生学会运用概念和公式解决相关问题,学会观察、归纳、反思,进一步培养学生灵活运用公式的能力以及分析问题和解决问题的能力.发展学生逻辑推理、直观想象、数学运算和数学建模的的核心素养.
设计意图:通过阅读读本,让学生明晰本阶段的学习目标,初步搭建学习内容的框架.
问题2:上节课我们学习了哪些知识?
师生活动:学生回顾并回答,教师完善.
设计意图:通过复习上节课内容,加强记忆,温故而知新.
问题3:类比等差数列,等比数列是不是也有下标和性质呢?
师生活动:学生思考,教师总结.
设计意图:通过该问题,引入新课.
【探究新知】
知识点1等比数列的性质
等比数列{an }中,若m,n,r,s∈N+,且m+n=r+s,则am·an=ar·as.
证明:设公比为q,因为,则,,,
所以,,
所以am·an=ar·as.
特别地,若2p=m+n,则ap2=aman.
设计意图:让学生会用等比数列的通项公式证明等比数列的下标和性质.
【练一练】递增等比数列{an }中,a3 +a6 =9,a4 a5=8,则数列{an }的公比为____.
预设的答案:由等比数列的性质知a4 a5= a3 a6=8,又a3 +a6 =9,且是递增数列,所以a3=1,a6=8,所以公比为2.
【巩固练习】
例1 用 10 000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
师生活动:让学生认真读题、审题,说出大致解题思路,教师完善.
预设的答案:(1)设这笔钱存n个月以后的本利和组成一个数列{an },
则{an }是等比数列,
首项a1=104 (1+0.400%),公比 q=1+0.400%,
所以a12=a1 q11 =104 (1+0.400%)12≈10 490.7.
所以,12个月后的利息为10 490.7-104≈491(元).
(2)设季度利率为r,这笔钱存n个季度以后的本利和组成一个数列{an },则{bn }也是一个等比数列,
首项,公比为1+r,
于是.
因此,以季度复利计息,存4个季度后的利息为元.
解不等式,得.
所以,当季度利率不小于1.206%时,按季结算的利息不少于按月结算的利息.
设计意图:通过运用等比数列模型解决实际问题,发展学生逻辑推理、数学抽象和数学建模的核心素养.增强学生的数学应用意识.
方法总结:一般地,涉及产值增长率、银行利息、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解.
例2 已知数列{an }的首项a1=3.
(1)若{an }为等差数列,公差d=2,证明数列{}为等比数列;
(2)若{an }为等比数列,公比,证明数列{}为等差数列.
师生活动:与学生一起分析:需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明.教师完善规范解题过程.
预设的答案:
证明(1):由a1=3,d=2,得{an }的通项公式为an=2n+1.
设bn=3an )=32n+1,则 :,
又 b1=33=27,
所以,{}是以 27为首项,9为公比的等比数列.
证明(2):由a1=3, ,得,
两边取以3为底的对数,得.
所以.又 ,
所以,{}是首项为1,公差为-2的等差数列.
设计意图:通过该典型例题,加深对等差与等比数列概念的理解,体会等差与等比数列的内在联系.提升学生逻辑推理、直观想象、数学抽象和数学运算的核心素养.
结论:1. 若数列{an }是等差数列,则数列{}是等比数列;
2.若数列{an }是各项均为正的等比数列,则数列{}是等差数列.
例3 某工厂去年12月试产1050个高新电子产品,产品合格率为.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高,产品合格率比前一个月增加,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
师生活动:与学生一起分析:设从今年1月起各月的产量及合格率分别构成数列{an},{bn },则各月不合格品的数量构成数列{an bn },由题意可知,数列{an }是等比数列,数列{bn}是等差数列,由于数列{an bn }既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.教师完善解题过程.
预设的答案:(1)设从今年1月起,各月的产量及不合格率分别构成数列{an},{bn}由题意,知
an=10501.05n-1,bn=1-[90%+0.4%(n-1)]=0.104-0.004n, 其中n=1,2,…,24,
则从今年1月起,各月不合格产品的数量是an bn=10501.05n-1(0.104-0.004n),
由计算工具计算(精确到0.1),并列表
观察发现,数列{an bn }先递增,在第6项以后递减,所以只要设法证明当n≥6时,{an bn }递减,且a13 b13<100即可.
由,
得n>5.
所以,当n≥6时,{an bn }递减,又a13 b13≈98<100,
所以当13≤n≤24时, an bn ≤a13 b13<100
所以,生产该产品一年后,月不合格的数量能控制在100个以内.
设计意图:通过该题,加深学生对等比数列的综合运用能力.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
方法总结:通常利用相邻项的大小比较得出数列的单调性.而数列两项大小比较可用作差法也可用作商法.
练习:教科书P34 练习2 、4
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
【课堂总结】
1.板书设计:
4. 3.1等比数列的概念(2)
一、探索新知 二、初步应用
1.等比数列的性质 例1
知识讲解1: 例2
例3
2.总结概括:
师生活动:学生总结,老师适当补充.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
3.课堂作业:教科书P34 练习1 、3 、5
【目标检测设计】
1.在流行病学中,基本传染数是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数. 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假定某种传染病的基本传染数,那么感染人数由1个初始感染者增加到2000人大约需要的传染轮数为( )
注:初始感染者传染个人为第一轮传染,这个人再传染个人为第二轮感染.
A.5 B.6 C.7 D.8
设计意图:让学生进一步巩固等比数列的定义及通项公式的实际应用.
2.已知等比数列的各项均为正数,且,则_____.
设计意图:让学生进一步巩固等比数列的性质.
3. 2017年,某县甲、乙两个林场森林木材的存量分别为16a和25a,
甲林场木材存量每年比上一年递增25%,而乙林场木材存量每年比上一年递减20%.
(1)哪一年两林场木材的总存量相等?
(2)两林场木材的总量到2021年能否翻一番?
设计意图:让学生进一步巩固等比数列通项公式的实际应用.
参考答案:1.B 2.10
3.解:(1)由题意可得
16a(1+25%)n-1=25a(1-20%)n-1,
解得n=2,
故到2019年两林场木材的总存量相等.
(2)令n=5,则,
故到2021年不能翻一番.
