4.3.2等比数列的前n项和 第2课时 教学设计
文档属性
| 名称 | 4.3.2等比数列的前n项和 第2课时 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-19 00:00:00 | ||
图片预览



文档简介
第四章 数列
《4.3.2等比数列的前n项和》教学设计
第2课时
1.掌握等比数列的前n项和公式及其应用.
2.能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.
教学重点:等比数列的前n项和公式及其应用
教学难点:运用等比数列解决实际问题.
PPT课件.
【新课导入】
问题1:阅读课本第38~40页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
师生活动:学生带着问题阅读课本,并在本节课中回答相应问题.
预设的答案:(1)本节课主要学习等比数列的前n项和公式.(2)学生在已学习等比数列前n项和公式的基础上,引导学生利用等比数列前n项和公式解决几何问题和实际应用问题,进一步培养学生灵活运用公式的能力.发展学生逻辑推理、直观想象、数学运算和数学建模的的核心素养.
设计意图:通过阅读读本,让学生明晰本阶段的学习目标,初步搭建学习内容的框架.
问题2:等比数列的前n项和公式是什么?
师生活动:学生回答,教师完善.
预设的答案:
已知量 首项a1、公比q(q≠1)与项数n 首项a1、末项an与公比q(q≠1) 首项a1、 公比q=1
求和公式
设计意图:通过回顾上节课内容,引入新课.
【探究新知】
问题3:若数列{an}是公比为q的等比数列,数列{bn}是公差为d的等差数列,如何求数列{an+bn}的前n项和Sn?
师生活动:学生思考后回答,教师完善.
预设的答案: Sn=(a1+b1 )+(a2+b2 )+ +(an+bn )
=(a1+a2+ +an ) + (b1+b2+ +bn )
设计意图:通过该问题让学生理解分组求和法,让学生会求一类可转化为等差数列和等比数列的求和的数列求和问题.
问题4:数列{an}的首项为1,且an+1=2an+1,你能求出该数列的通项公式吗?
师生活动:学生分组讨论,派代表发表看法,教师完善.
预设的答案:该数列既不是等差数列也不是等比数列,如果两边同加上1可得:
an+1+1=2(an+1),又a1+1=2,所以数列{an+1}是以2为首项,公比为2的等比数列,
所以an+1=2n,所以an=2n-1,即数列{an}的通项公式为an=2n-1.
设计意图:让学生理解用构造法求一类数列的通项公式,增强学生的逻辑推理能力.
【巩固练习】
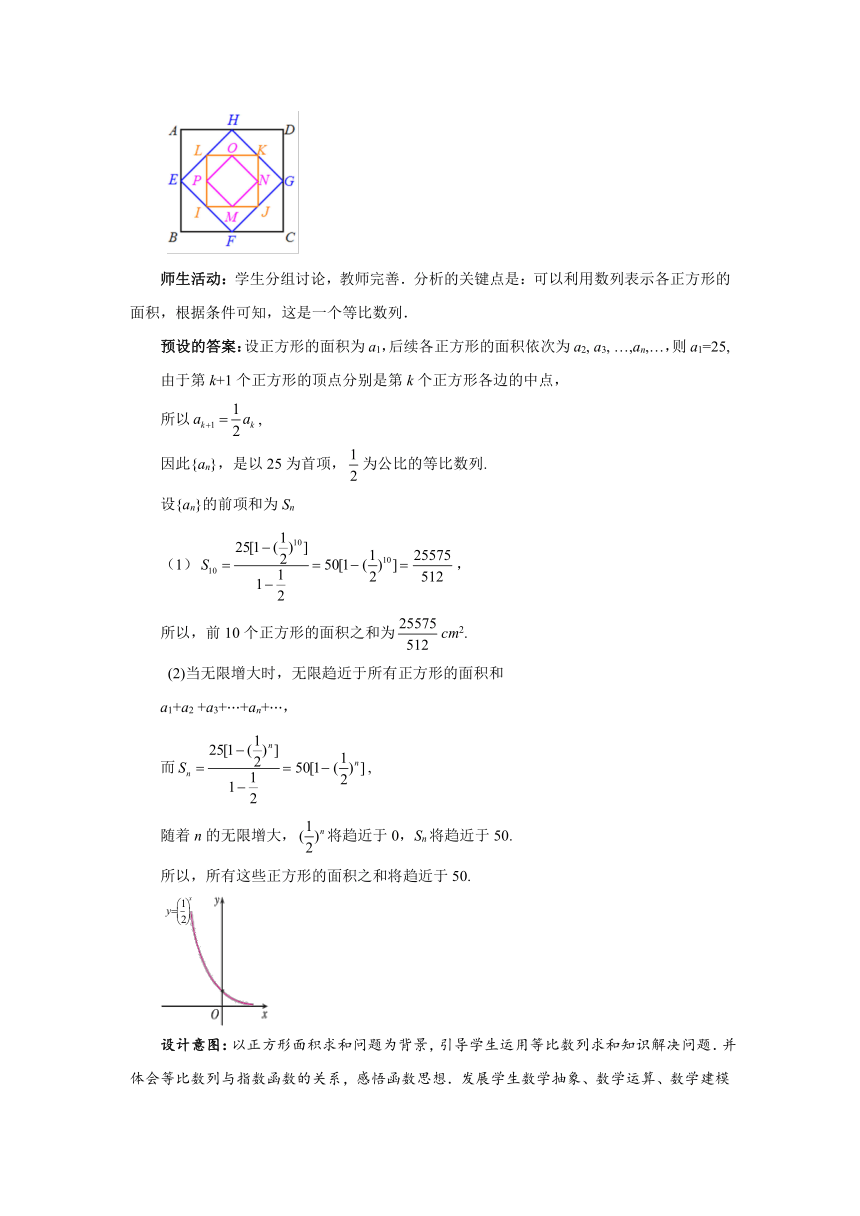
例1如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E,F,G,H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I,J,K,L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?
师生活动:学生分组讨论,教师完善.分析的关键点是:可以利用数列表示各正方形的面积,根据条件可知,这是一个等比数列.
预设的答案:设正方形的面积为a1,后续各正方形的面积依次为a2, a3, …,an,…,则a1=25,
由于第k+1个正方形的顶点分别是第k个正方形各边的中点,
所以,
因此{an},是以25为首项,为公比的等比数列.
设{an}的前项和为Sn
(1),
所以,前10个正方形的面积之和为cm2.
(2)当无限增大时,无限趋近于所有正方形的面积和
a1+a2 +a3+ +an+ ,
而,
随着n的无限增大,将趋近于0,Sn将趋近于50.
所以,所有这些正方形的面积之和将趋近于50.
设计意图:以正方形面积求和问题为背景,引导学生运用等比数列求和知识解决问题.并体会等比数列与指数函数的关系,感悟函数思想.发展学生数学抽象、数学运算、数学建模的核心素养.
例2 去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请你测算一下从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
师生活动:学生读题,审题,分组讨论,派代表发言.教师完善.
预设的答案:设从今年起每年生活垃圾的总量(单位:万吨)构成数列{an},每年以环保方式处理的垃圾量(单位:万吨)构成数列{bn},n年内通过填埋方式处理的垃圾总量为Sn(单位:万吨),则, bn=6+1.5 n ,
Sn=(a1-b1 )+(a2-b2 )+ +(an-bn )
=(a1+a2+ +an )-(b1+b2+ +bn )
=(20×1.05+20×1.052+ +20×1.05n )-(7.5+9+ 6+1.5n)
当n=5时,S5≈63.5
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为 63.5万吨.
设计意图:以生活中的垃圾处理为背景,引导学生运用等比数列求和知识解决实际问题.并掌握分组求和法.发展学生数学抽象、数学运算、数学建模的核心素养.
方法总结:解决数列应用题时:
一是明确问题属于哪类应用问题,即明确是等差数列还是等比数列问题,还是含有递推关系的数列问题;
二是明确是求an,还是求Sn.细胞繁殖、利率、增长率等问题一般为等比数列问题.
例3 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8% ,且在每年年底卖出100头牛.设牧场从今年起每年年初的计划存栏数依次为c1,c2 ,c3,…
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2)将(1)中的递推公式表示成c n+1 -k=r(cn-k)的形式,其中k,r为常数;
(3)求S10=c1+c2 +c3+ +c10的值(精确到1).
师生活动:学生读题,审题,分组讨论,派代表发言.教师分析:(1)可以利用“每年存栏数的增长率为8%”和“每年年底卖出100头”建立c n+1与cn的关系;(2)这是待定系数法的应用,可以将它还原为(1)中的递推公式形式,通过比较系数,得到方程组;(3)利用(2)的结论可得出解答.
预设的答案:(1)由题意,得c1=1200,并且cn+1=1.08cn-100.①
(2)将cn+1-k=r(cn-k)化成c n+1 =rcn-rk+k.②
比较①②的系数,可得
解这个方程组,得
所以(1)中的递推公式可以化为cn+1-1250=1.08(cn-1250).
(3)由(2)可知,数列{cn-1250}是以-50为首项,1.08为公比的等比数列,则
(c1-1250)+(c2 -1250)+(c3-1250)+ +(cn-1250)
.
所以S10=c1+c2 +c3+ +c10≈1250×10-724.8=11775.7≈11776.
设计意图:以牧场中牛的繁殖问题为背景,引导学生运用等比数列求和知识解决问题,并学会运用构造法,构造等比数列解决问题.发展学生数学抽象、数学运算、数学建模的核心素养.
方法总结:在解决实际问题时,有时不容易发现呈等差关系或等比关系变化的量,但可以发现某些量的递推关系.这时,往往可以先构建一个用递推关系表达的数列,再尝试通过代数变换,把这个数列转化为等差数列或等比数列,或等差数列与等比数列的线性组合.
对于数列{cn}满足:cn+1 =rcn+m ,先通过引入参数,建立一个含cn+1与cn的等比关系,再求出其中的参数,这实际上是待定系数法,即:cn+1-k=r(cn-k),先求出数列{cn-k}的通项公式,进而求得数列{cn}的通项公式.
练习:教科书P40 练习1 ~4
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
【课堂总结】
1.板书设计:
4. 3.2等比数列的前n项和(2)
一、探索新知 二、初步应用
1.分组求和法 例1
知识讲解1: 例2
2.构造法求数列通项公式 例3
知识讲解2:
2.总结概括:
(1)掌握用等比数列知识解决增长率等问题的数学模型,尤其要注意公比与项数的选取;
(2)根据实际问题,先分清等比数列与等差数列, 再建立不同的数学模型;
(3)通过实际问题,发现等差数列与等比数列的不同特点.
师生活动:学生总结,老师适当补充.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
3.课堂作业:教科书P41 习题4.3 6 、7 、8 、9
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。
【目标检测设计】
1.等比数列{an}的公比为q(q≠1),则数列a3,a6,a9,…,a3n,…的前n项和为( )
A. B.
C. D.
设计意图:让学生进一步巩固等比数列的前n项和公式.
2.记Sn为数列{an}的前n项和.若Sn=2an+1,则S6=________.
设计意图:让学生进一步巩固和项关系以及等比数列的前n项和公式.
3. 某地投入资金进行生态环境建设,并以此发展旅游产业.据规划,本年度投入800万元,以后每年投入将比上一年减少,本年度当地旅游业收入估计为400万元.由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上一年增长.求n年内的总投入与n年内旅游业的总收入.
设计意图:通过本题,提升学生对等比数列求和公式的综合运用能力,增强分析问题解决问题的能力.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
参考答案:1.C 等比数列中,序号成等差数列,则项仍成等比数列,则a3,a6,…,a3n是等比数列,且首项为a3,公比为,再用等比数列的前n项和公式求解,即Sn=,故选C.
2.-63 因为Sn=2an+1,所以当n=1时,a1=2a1+1,解得a1=-1,
当n≥2时,an=Sn-Sn-1=2an+1-(2an-1+1),所以an=2an-1,所以数列{an}是以-1为首项,2为公比的等比数列,所以an=-2n-1,所以S6=.
3.解:由题意知第1年投入800万元,
第2年投入800×万元,
……
第n年投入800×n-1万元,
所以每年的投入资金数构成首项为800,公比为的等比数列.
所以n年内的总投入Sn=800+800×+…+800×n-1=4 000× (万元).
由题意知,第1年旅游业的收入为400万元,
第2年旅游业的收入为万元,
……
第n年旅游业的收入为万元,
所以每年的旅游业收入资金数构成首项为400,
公比为的等比数列.
所以n年内旅游业的总收入
Tn=400+400×+…+400×n-1=1 600× (万元).
故n年内的总投入为4 000×万元,
n年内旅游业的总收入为1 600×万元.
《4.3.2等比数列的前n项和》教学设计
第2课时
1.掌握等比数列的前n项和公式及其应用.
2.能在具体的问题情境中,发现数列的等比关系,并解决相应的问题.
教学重点:等比数列的前n项和公式及其应用
教学难点:运用等比数列解决实际问题.
PPT课件.
【新课导入】
问题1:阅读课本第38~40页,回答下列问题:
(1)本节将要探究哪类问题?
(2)本节探究的起点是什么?目标是什么?
师生活动:学生带着问题阅读课本,并在本节课中回答相应问题.
预设的答案:(1)本节课主要学习等比数列的前n项和公式.(2)学生在已学习等比数列前n项和公式的基础上,引导学生利用等比数列前n项和公式解决几何问题和实际应用问题,进一步培养学生灵活运用公式的能力.发展学生逻辑推理、直观想象、数学运算和数学建模的的核心素养.
设计意图:通过阅读读本,让学生明晰本阶段的学习目标,初步搭建学习内容的框架.
问题2:等比数列的前n项和公式是什么?
师生活动:学生回答,教师完善.
预设的答案:
已知量 首项a1、公比q(q≠1)与项数n 首项a1、末项an与公比q(q≠1) 首项a1、 公比q=1
求和公式
设计意图:通过回顾上节课内容,引入新课.
【探究新知】
问题3:若数列{an}是公比为q的等比数列,数列{bn}是公差为d的等差数列,如何求数列{an+bn}的前n项和Sn?
师生活动:学生思考后回答,教师完善.
预设的答案: Sn=(a1+b1 )+(a2+b2 )+ +(an+bn )
=(a1+a2+ +an ) + (b1+b2+ +bn )
设计意图:通过该问题让学生理解分组求和法,让学生会求一类可转化为等差数列和等比数列的求和的数列求和问题.
问题4:数列{an}的首项为1,且an+1=2an+1,你能求出该数列的通项公式吗?
师生活动:学生分组讨论,派代表发表看法,教师完善.
预设的答案:该数列既不是等差数列也不是等比数列,如果两边同加上1可得:
an+1+1=2(an+1),又a1+1=2,所以数列{an+1}是以2为首项,公比为2的等比数列,
所以an+1=2n,所以an=2n-1,即数列{an}的通项公式为an=2n-1.
设计意图:让学生理解用构造法求一类数列的通项公式,增强学生的逻辑推理能力.
【巩固练习】
例1如图,正方形ABCD的边长为5cm,取正方形ABCD各边的中点E,F,G,H,作第2个正方形EFGH,然后再取正方形EFGH各边的中点I,J,K,L,作第3个正方形IJKL,依此方法一直继续下去.
(1) 求从正方形ABCD开始,连续10个正方形的面积之和;
(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?
师生活动:学生分组讨论,教师完善.分析的关键点是:可以利用数列表示各正方形的面积,根据条件可知,这是一个等比数列.
预设的答案:设正方形的面积为a1,后续各正方形的面积依次为a2, a3, …,an,…,则a1=25,
由于第k+1个正方形的顶点分别是第k个正方形各边的中点,
所以,
因此{an},是以25为首项,为公比的等比数列.
设{an}的前项和为Sn
(1),
所以,前10个正方形的面积之和为cm2.
(2)当无限增大时,无限趋近于所有正方形的面积和
a1+a2 +a3+ +an+ ,
而,
随着n的无限增大,将趋近于0,Sn将趋近于50.
所以,所有这些正方形的面积之和将趋近于50.
设计意图:以正方形面积求和问题为背景,引导学生运用等比数列求和知识解决问题.并体会等比数列与指数函数的关系,感悟函数思想.发展学生数学抽象、数学运算、数学建模的核心素养.
例2 去年某地产生的生活垃圾为20万吨,其中14万吨垃圾以填埋方式处理,6万吨垃圾以环保方式处理.预计每年生活垃圾的总量递增5%,同时,通过环保方式处理的垃圾量每年增加1.5万吨.为了确定处理生活垃圾的预算,请你测算一下从今年起5年内通过填埋方式处理的垃圾总量(精确到0.1万吨).
师生活动:学生读题,审题,分组讨论,派代表发言.教师完善.
预设的答案:设从今年起每年生活垃圾的总量(单位:万吨)构成数列{an},每年以环保方式处理的垃圾量(单位:万吨)构成数列{bn},n年内通过填埋方式处理的垃圾总量为Sn(单位:万吨),则, bn=6+1.5 n ,
Sn=(a1-b1 )+(a2-b2 )+ +(an-bn )
=(a1+a2+ +an )-(b1+b2+ +bn )
=(20×1.05+20×1.052+ +20×1.05n )-(7.5+9+ 6+1.5n)
当n=5时,S5≈63.5
所以,从今年起5年内,通过填埋方式处理的垃圾总量约为 63.5万吨.
设计意图:以生活中的垃圾处理为背景,引导学生运用等比数列求和知识解决实际问题.并掌握分组求和法.发展学生数学抽象、数学运算、数学建模的核心素养.
方法总结:解决数列应用题时:
一是明确问题属于哪类应用问题,即明确是等差数列还是等比数列问题,还是含有递推关系的数列问题;
二是明确是求an,还是求Sn.细胞繁殖、利率、增长率等问题一般为等比数列问题.
例3 某牧场今年初牛的存栏数为1200,预计以后每年存栏数的增长率为8% ,且在每年年底卖出100头牛.设牧场从今年起每年年初的计划存栏数依次为c1,c2 ,c3,…
(1)写出一个递推公式,表示cn+1与cn之间的关系;
(2)将(1)中的递推公式表示成c n+1 -k=r(cn-k)的形式,其中k,r为常数;
(3)求S10=c1+c2 +c3+ +c10的值(精确到1).
师生活动:学生读题,审题,分组讨论,派代表发言.教师分析:(1)可以利用“每年存栏数的增长率为8%”和“每年年底卖出100头”建立c n+1与cn的关系;(2)这是待定系数法的应用,可以将它还原为(1)中的递推公式形式,通过比较系数,得到方程组;(3)利用(2)的结论可得出解答.
预设的答案:(1)由题意,得c1=1200,并且cn+1=1.08cn-100.①
(2)将cn+1-k=r(cn-k)化成c n+1 =rcn-rk+k.②
比较①②的系数,可得
解这个方程组,得
所以(1)中的递推公式可以化为cn+1-1250=1.08(cn-1250).
(3)由(2)可知,数列{cn-1250}是以-50为首项,1.08为公比的等比数列,则
(c1-1250)+(c2 -1250)+(c3-1250)+ +(cn-1250)
.
所以S10=c1+c2 +c3+ +c10≈1250×10-724.8=11775.7≈11776.
设计意图:以牧场中牛的繁殖问题为背景,引导学生运用等比数列求和知识解决问题,并学会运用构造法,构造等比数列解决问题.发展学生数学抽象、数学运算、数学建模的核心素养.
方法总结:在解决实际问题时,有时不容易发现呈等差关系或等比关系变化的量,但可以发现某些量的递推关系.这时,往往可以先构建一个用递推关系表达的数列,再尝试通过代数变换,把这个数列转化为等差数列或等比数列,或等差数列与等比数列的线性组合.
对于数列{cn}满足:cn+1 =rcn+m ,先通过引入参数,建立一个含cn+1与cn的等比关系,再求出其中的参数,这实际上是待定系数法,即:cn+1-k=r(cn-k),先求出数列{cn-k}的通项公式,进而求得数列{cn}的通项公式.
练习:教科书P40 练习1 ~4
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
【课堂总结】
1.板书设计:
4. 3.2等比数列的前n项和(2)
一、探索新知 二、初步应用
1.分组求和法 例1
知识讲解1: 例2
2.构造法求数列通项公式 例3
知识讲解2:
2.总结概括:
(1)掌握用等比数列知识解决增长率等问题的数学模型,尤其要注意公比与项数的选取;
(2)根据实际问题,先分清等比数列与等差数列, 再建立不同的数学模型;
(3)通过实际问题,发现等差数列与等比数列的不同特点.
师生活动:学生总结,老师适当补充.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
3.课堂作业:教科书P41 习题4.3 6 、7 、8 、9
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养。
【目标检测设计】
1.等比数列{an}的公比为q(q≠1),则数列a3,a6,a9,…,a3n,…的前n项和为( )
A. B.
C. D.
设计意图:让学生进一步巩固等比数列的前n项和公式.
2.记Sn为数列{an}的前n项和.若Sn=2an+1,则S6=________.
设计意图:让学生进一步巩固和项关系以及等比数列的前n项和公式.
3. 某地投入资金进行生态环境建设,并以此发展旅游产业.据规划,本年度投入800万元,以后每年投入将比上一年减少,本年度当地旅游业收入估计为400万元.由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上一年增长.求n年内的总投入与n年内旅游业的总收入.
设计意图:通过本题,提升学生对等比数列求和公式的综合运用能力,增强分析问题解决问题的能力.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
参考答案:1.C 等比数列中,序号成等差数列,则项仍成等比数列,则a3,a6,…,a3n是等比数列,且首项为a3,公比为,再用等比数列的前n项和公式求解,即Sn=,故选C.
2.-63 因为Sn=2an+1,所以当n=1时,a1=2a1+1,解得a1=-1,
当n≥2时,an=Sn-Sn-1=2an+1-(2an-1+1),所以an=2an-1,所以数列{an}是以-1为首项,2为公比的等比数列,所以an=-2n-1,所以S6=.
3.解:由题意知第1年投入800万元,
第2年投入800×万元,
……
第n年投入800×n-1万元,
所以每年的投入资金数构成首项为800,公比为的等比数列.
所以n年内的总投入Sn=800+800×+…+800×n-1=4 000× (万元).
由题意知,第1年旅游业的收入为400万元,
第2年旅游业的收入为万元,
……
第n年旅游业的收入为万元,
所以每年的旅游业收入资金数构成首项为400,
公比为的等比数列.
所以n年内旅游业的总收入
Tn=400+400×+…+400×n-1=1 600× (万元).
故n年内的总投入为4 000×万元,
n年内旅游业的总收入为1 600×万元.
