20.3 课题学习 体质健康测试中的数据分析 课件(共33张PPT)
文档属性
| 名称 | 20.3 课题学习 体质健康测试中的数据分析 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-18 20:37:31 | ||
图片预览








文档简介
(共33张PPT)
20.3 课题学习
体质健康测试中的数据分析
人教版八年级上册
知识回顾
方差是反映一组数据的 ,也可称反映数据的 程度的一个量,方差越大,数据的波动 ,也越不稳定或不整齐;方差 ,数据的波动越小,也越稳定或整齐.
波动大小
离散
越大
越小
.
方差的简化计算公式为:
教学目标
1.体验数据收集、整理和分析的全过程.
2.学会一套完整的数据调查流程.
新知导入
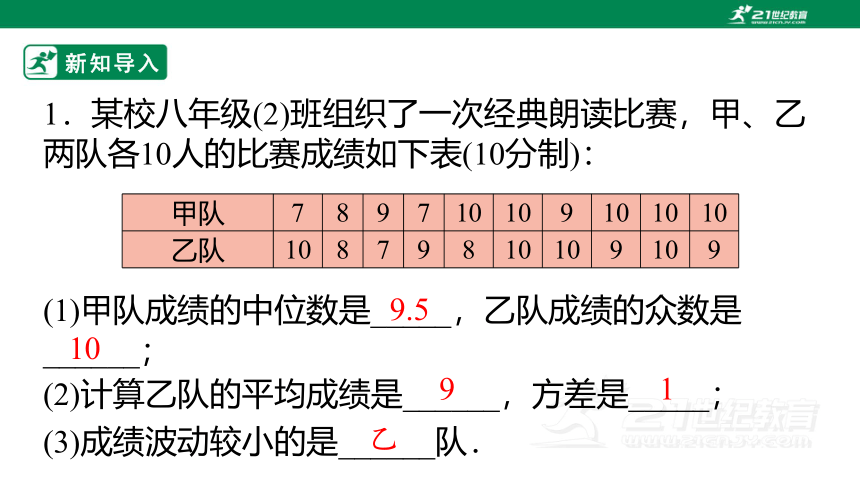
1.某校八年级(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 7 8 9 7 10 10 9 10 10 10
乙队 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是_____,乙队成绩的众数是______;
9.5
10
(2)计算乙队的平均成绩是______,方差是_____;
(3)成绩波动较小的是______队.
乙
9
1
新知探究
收集近两年你校七年级学生的《体质健康登记表》,分析登记表中的数据,对你校七年级学生的体质健康情况进行评定,从而提出增强学生体质健康的建议.
新知探究
假设某学校七年级有4个班,共180人,其中男生85人,女生95人. 完成《体质健康登记表》的调查.
思考
思考完成并交流展示.
这个调查如何完成呢?
新知探究
从全校七年级的各班分别抽取5名男生和5名女生,组成一个容量为40的样本.
按照各班的学号,分别在每个班抽取学号排在最前面的5名男生和5名女生.
一.收集数据
1、确定样本
2、确定抽取样本的方法
新知探究
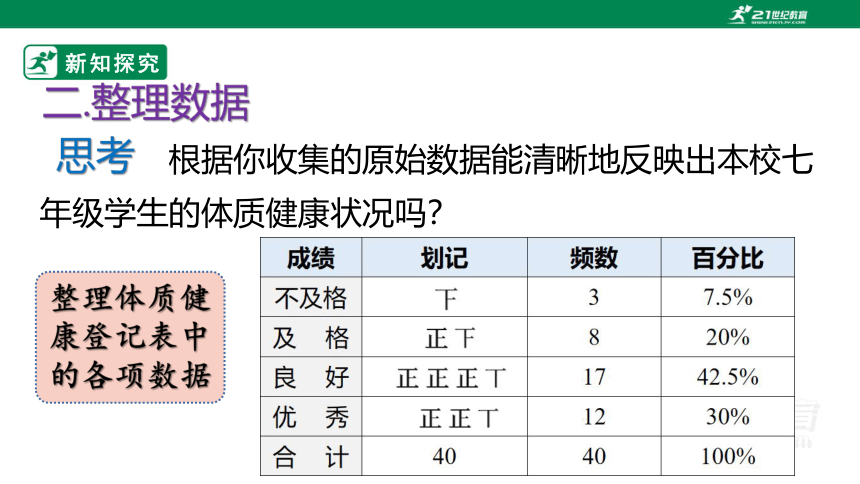
二.整理数据
根据你收集的原始数据能清晰地反映出本校七年级学生的体质健康状况吗?
思考
整理体质健康登记表中的各项数据
新知探究
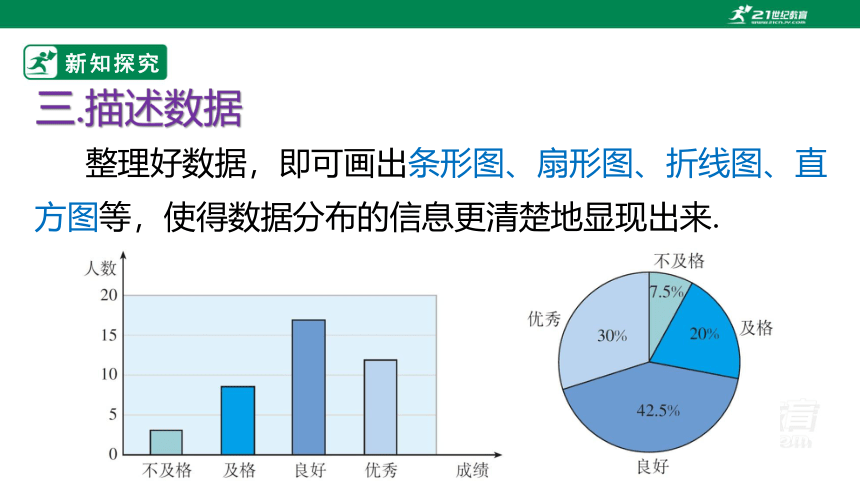
三.描述数据
整理好数据,即可画出条形图、扇形图、折线图、直方图等,使得数据分布的信息更清楚地显现出来.
新知探究
四.分析数据
根据原始数据或上面的各种统计图表,计算各组数据的平均数、中位数、众数、方差等,通过分析图表和计算得出结论.
例如,根据以上各表可知,样本的体质健康成绩达到良好的最多,有17人,良好及以上的有29人,约占统计人数的70%左右.由此可以估计全校七年级学生的体质健康成绩的结果.
新知探究
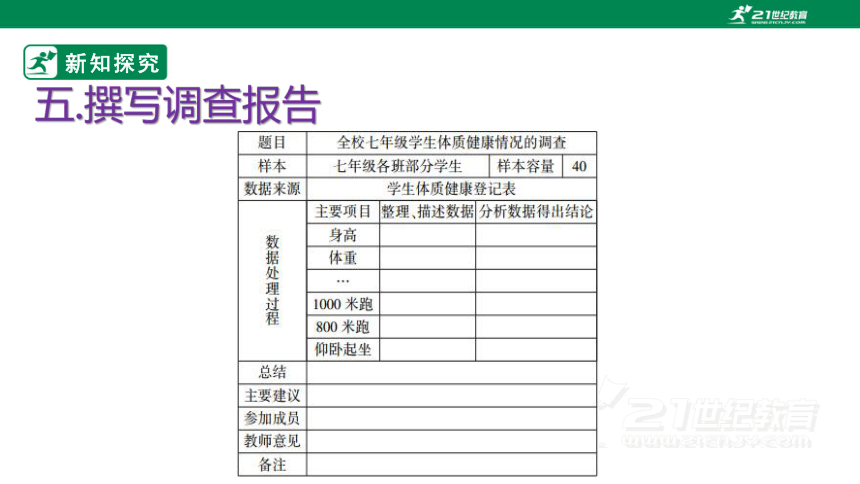
五.撰写调查报告
新知探究
六.交流
写出活动总结,向全班同学介绍本小组的调查过程,展示调查结果,交流通过数据处理寻找规律、得出结论的感受.
新知小结
分析数据一般要计算各组数据的 、 、
、 、等,通过分析图表和计算结果得出结论
数据分析的一般步骤: 、 、
、 .
描述数据的方法:利用 、 、 、
、 等,使得数据分布的信息更清楚地显现出来.
收集数据
整理数据
描述数据
分析数据
表格
画出条形图
扇形图
折线图
直方图
平均数
中位数
众数
方差
新知练习
1.对八年级(2)班 40 名学生的平均身高进行调查研究,写出调查过程和结果,并汇总到一起,得到全班同学身高的一个“平均情况”.
根据研究性学习的一般步骤,对活动小组的同学进行合理分工,并明确调查活动的基本要求,必要时还可以提示活动中的有关注意事项.
新知练习
解析:(1)收集数据
①确定样本:在本班 40 名同学中分别随机地抽取 10 名男生和 6 名女生,组成一个容量为 16 的样本.
②确定抽取样本的方法:从学号为偶数的男生中分别抽取 5 名较小学号的男生和 5 名较大学号的男生,确定出 10 名男同学,从学号是 3 的倍数的女生中,确定出 6 名女同学(确保这些同学的年龄相同).
新知练习
(2)整理数据
分析样本中的身高,根据数据进行分组统计.
样本身高分组 男生 百分比 女生 百分比
150-155 1 10% 1 16.7%
155-160 2 20% 1 16.7%
160-165 4 40% 2 33.3%
165-170 2 20% 2 33.3%
170以上 1 10% 0 0%
合计 10 33.3% 6 100%
新知练习
(3)描述数据
将上述表格的数据用统计图表示出来.
身高(cm)
人数
150-155
0
1
2
3
4
男生
女生
155-160
160-165
165-170
170以上
新知练习
(4)分析数据
分别计算男生、女生身高的平均数、方差、众数、中位数等数据,综合以上各种数据进行全面、科学的分析统计.
(5)撰写调查报告
根据以上步骤得出的结论,写出一个总结性的报告.
新知练习
通过计算将平均数、方差补充完整.
新知练习
(6)交流
通过课题研究,学习小组对撰写的调查报告进行互相的交流和评价,感受数据统计的实用性,体验学习探究性活动的乐趣.
新知典例
例1 某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分10分):
方案1:所有评委所给分的平均数.
方案2:在所有评委所给分中,去掉一个最高分和一个最低分,
然后再计算其余给分的平均数.
方案4:所有评委所给分的众数.
方案3:所有评委所给分的中位数.
新知典例
为了探究上述方案的合理性,先对某个同学的演讲成绩进行统计实验.下面是这个同学的得分统计图:
(1)分别按上述4个方案计算这个同学演讲的最后得分;
解:方案1:7.7
方案2:8
方案3:8
方案4:8或8.4
新知典例
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学的演讲的最后得分.
所以方案4不适合作为最后得分的方案
解:因为方案1的平均数受极端值的影响,不能反映这组数据的“平均水平”,
所以方案1不符合作为最后得分的方案;
方案4中的众数有两个,众数失去了实际意义,
新知典例
例2 甲、乙两位同学本学年11次数学单元测验成绩(整数)的统计如图所示:
新知典例
(1)分别求他们的平均分;
=96(分)
×(98+100+100+90+96+91+89+99+100+100+93)
_
x
甲
__
11
1
=
=96(分)
解:
×(98+99+96+94+95+92+92+98+96+99+97)
__
11
1
=
_
x
乙
新知典例
(2)请你从中挑选一人参加数学“希望杯”竞赛,并说明你挑选的理由.
解:应选甲同学参加比赛,
因为甲超过平均分的次数比乙多,比乙更容易获得高分.
(答案不唯一,言之有理即可)
课堂总结
体质健康测试中的数据分析
数据分析
描述数据
分析数据
收集数据、整理数据、描述数据、分析数据
表格,画出条形图、扇形图、折线图、直方图
平均数、中位数、众数与方差
课堂练习
1.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.方差
C.平均数 D.中位数
2.某交警在一个路口统计的某时段来往车辆的车速情况如表:
车速(km/h) 48 49 50 51 52
车辆数(辆) 5 4 8 2 1
则上述车速的中位数和众数分别是(单位:km/h)( )
A.50,8 B.50,50
C.49,50 D.49,8
D
B
课堂练习
(1)前10株西红柿秧上小西红柿个数的平均数是______
3.阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数分别为:
32,39,45,55,60,54,60,28,56,41,51,36,44,46,40,53,37,47,45,46.
47
中位数是______,众数是______;
49.5
60
课堂练习
(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图;
个数分组 28≤x<36 36≤x<44 44≤x<52 52≤x<60 60≤x<68
频数 2 2
5
7
4
课堂练习
(3)试通过频数分布直方图分析此大棚中西红柿的长势.
西红柿的个数分布合理,中间多,两端少.
解:此大棚的西红柿长势普遍较好,最少都有28个;
西红柿个数最集中的株数在第三组,共7株;
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
20.3 课题学习
体质健康测试中的数据分析
人教版八年级上册
知识回顾
方差是反映一组数据的 ,也可称反映数据的 程度的一个量,方差越大,数据的波动 ,也越不稳定或不整齐;方差 ,数据的波动越小,也越稳定或整齐.
波动大小
离散
越大
越小
.
方差的简化计算公式为:
教学目标
1.体验数据收集、整理和分析的全过程.
2.学会一套完整的数据调查流程.
新知导入
1.某校八年级(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 7 8 9 7 10 10 9 10 10 10
乙队 10 8 7 9 8 10 10 9 10 9
(1)甲队成绩的中位数是_____,乙队成绩的众数是______;
9.5
10
(2)计算乙队的平均成绩是______,方差是_____;
(3)成绩波动较小的是______队.
乙
9
1
新知探究
收集近两年你校七年级学生的《体质健康登记表》,分析登记表中的数据,对你校七年级学生的体质健康情况进行评定,从而提出增强学生体质健康的建议.
新知探究
假设某学校七年级有4个班,共180人,其中男生85人,女生95人. 完成《体质健康登记表》的调查.
思考
思考完成并交流展示.
这个调查如何完成呢?
新知探究
从全校七年级的各班分别抽取5名男生和5名女生,组成一个容量为40的样本.
按照各班的学号,分别在每个班抽取学号排在最前面的5名男生和5名女生.
一.收集数据
1、确定样本
2、确定抽取样本的方法
新知探究
二.整理数据
根据你收集的原始数据能清晰地反映出本校七年级学生的体质健康状况吗?
思考
整理体质健康登记表中的各项数据
新知探究
三.描述数据
整理好数据,即可画出条形图、扇形图、折线图、直方图等,使得数据分布的信息更清楚地显现出来.
新知探究
四.分析数据
根据原始数据或上面的各种统计图表,计算各组数据的平均数、中位数、众数、方差等,通过分析图表和计算得出结论.
例如,根据以上各表可知,样本的体质健康成绩达到良好的最多,有17人,良好及以上的有29人,约占统计人数的70%左右.由此可以估计全校七年级学生的体质健康成绩的结果.
新知探究
五.撰写调查报告
新知探究
六.交流
写出活动总结,向全班同学介绍本小组的调查过程,展示调查结果,交流通过数据处理寻找规律、得出结论的感受.
新知小结
分析数据一般要计算各组数据的 、 、
、 、等,通过分析图表和计算结果得出结论
数据分析的一般步骤: 、 、
、 .
描述数据的方法:利用 、 、 、
、 等,使得数据分布的信息更清楚地显现出来.
收集数据
整理数据
描述数据
分析数据
表格
画出条形图
扇形图
折线图
直方图
平均数
中位数
众数
方差
新知练习
1.对八年级(2)班 40 名学生的平均身高进行调查研究,写出调查过程和结果,并汇总到一起,得到全班同学身高的一个“平均情况”.
根据研究性学习的一般步骤,对活动小组的同学进行合理分工,并明确调查活动的基本要求,必要时还可以提示活动中的有关注意事项.
新知练习
解析:(1)收集数据
①确定样本:在本班 40 名同学中分别随机地抽取 10 名男生和 6 名女生,组成一个容量为 16 的样本.
②确定抽取样本的方法:从学号为偶数的男生中分别抽取 5 名较小学号的男生和 5 名较大学号的男生,确定出 10 名男同学,从学号是 3 的倍数的女生中,确定出 6 名女同学(确保这些同学的年龄相同).
新知练习
(2)整理数据
分析样本中的身高,根据数据进行分组统计.
样本身高分组 男生 百分比 女生 百分比
150-155 1 10% 1 16.7%
155-160 2 20% 1 16.7%
160-165 4 40% 2 33.3%
165-170 2 20% 2 33.3%
170以上 1 10% 0 0%
合计 10 33.3% 6 100%
新知练习
(3)描述数据
将上述表格的数据用统计图表示出来.
身高(cm)
人数
150-155
0
1
2
3
4
男生
女生
155-160
160-165
165-170
170以上
新知练习
(4)分析数据
分别计算男生、女生身高的平均数、方差、众数、中位数等数据,综合以上各种数据进行全面、科学的分析统计.
(5)撰写调查报告
根据以上步骤得出的结论,写出一个总结性的报告.
新知练习
通过计算将平均数、方差补充完整.
新知练习
(6)交流
通过课题研究,学习小组对撰写的调查报告进行互相的交流和评价,感受数据统计的实用性,体验学习探究性活动的乐趣.
新知典例
例1 某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分10分):
方案1:所有评委所给分的平均数.
方案2:在所有评委所给分中,去掉一个最高分和一个最低分,
然后再计算其余给分的平均数.
方案4:所有评委所给分的众数.
方案3:所有评委所给分的中位数.
新知典例
为了探究上述方案的合理性,先对某个同学的演讲成绩进行统计实验.下面是这个同学的得分统计图:
(1)分别按上述4个方案计算这个同学演讲的最后得分;
解:方案1:7.7
方案2:8
方案3:8
方案4:8或8.4
新知典例
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学的演讲的最后得分.
所以方案4不适合作为最后得分的方案
解:因为方案1的平均数受极端值的影响,不能反映这组数据的“平均水平”,
所以方案1不符合作为最后得分的方案;
方案4中的众数有两个,众数失去了实际意义,
新知典例
例2 甲、乙两位同学本学年11次数学单元测验成绩(整数)的统计如图所示:
新知典例
(1)分别求他们的平均分;
=96(分)
×(98+100+100+90+96+91+89+99+100+100+93)
_
x
甲
__
11
1
=
=96(分)
解:
×(98+99+96+94+95+92+92+98+96+99+97)
__
11
1
=
_
x
乙
新知典例
(2)请你从中挑选一人参加数学“希望杯”竞赛,并说明你挑选的理由.
解:应选甲同学参加比赛,
因为甲超过平均分的次数比乙多,比乙更容易获得高分.
(答案不唯一,言之有理即可)
课堂总结
体质健康测试中的数据分析
数据分析
描述数据
分析数据
收集数据、整理数据、描述数据、分析数据
表格,画出条形图、扇形图、折线图、直方图
平均数、中位数、众数与方差
课堂练习
1.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.方差
C.平均数 D.中位数
2.某交警在一个路口统计的某时段来往车辆的车速情况如表:
车速(km/h) 48 49 50 51 52
车辆数(辆) 5 4 8 2 1
则上述车速的中位数和众数分别是(单位:km/h)( )
A.50,8 B.50,50
C.49,50 D.49,8
D
B
课堂练习
(1)前10株西红柿秧上小西红柿个数的平均数是______
3.阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数分别为:
32,39,45,55,60,54,60,28,56,41,51,36,44,46,40,53,37,47,45,46.
47
中位数是______,众数是______;
49.5
60
课堂练习
(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图;
个数分组 28≤x<36 36≤x<44 44≤x<52 52≤x<60 60≤x<68
频数 2 2
5
7
4
课堂练习
(3)试通过频数分布直方图分析此大棚中西红柿的长势.
西红柿的个数分布合理,中间多,两端少.
解:此大棚的西红柿长势普遍较好,最少都有28个;
西红柿个数最集中的株数在第三组,共7株;
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
